ФІЗИЧНА ХІМІЯ МІЖФАЗНИХ ЯВИЩ Поверхневі явища у конденсованих

ФІЗИЧНА ХІМІЯ МІЖФАЗНИХ ЯВИЩ Поверхневі явища у конденсованих фазах

Збільшення площі поверхні кулі при збільшенні радіусу r до (r + dr) Збільшення об’єму кулі при збільшенні радіусу r до (r + dr) Загальна зміна поверхневої енергії Робота стиснення (розширення) системи

Загальна зміна поверхневої енергії Робота стиснення (розширення) системи Рівняння Юнга-Лапласа:

Рівняння Юнга-Лапласа: Для несферичних тіл: Для циліндру радіуса r: r1 = r, r2 = ∞:

Метод сталагмометрії При відриві краплини:

Капілярне підняття рідини (R – радіус капіляра, r – радіус кривизни,  - кут змочування) Капілярне підняття (а) та опущення (б) При повному змочуванні  = 0 та cos  = 1 Для ртуті  = 465·10-3 Дж/м2 при 450 атм: входження у пори ~ 15 нм

Збільшення тиску насиченої пари над рідиною Додатковий тиск на поверхню рідини веде до збільшення тиску насиченої пари над рідиною: Vm - мольний об'єм конденсованої фази Для плоскої поверхні r1 = r2 = ∞ і P = 0 У випадку випуклого меніску за рахунок кривизни поверхні виникає так званий “тиск Лапласа” згідно до рівняння Юнга-Лапласа: Рівняння Томсона (Кельвіна): pn – тиск насиченої пари над випуклою поверхнею

При r = 10-6 м pn/p0 = 1,001 Рівняння Томсона (Кельвіна): Підвищення тиску насиченої пари над малими краплинами призводить до агрегації рідини у великі краплі (атмосферні осади, перегонка) При r = 10-7 м pn/p0 = 1,011 При r = 10-8 м pn/p0 = 1,114 Для ввігнутих менісків рідин:

Рівновага між поверхневим шаром та об'ємом для багатокомпонентної гомогенної конденсованої системи xi – мольна частка компонента в об'ємі; yi – мольна частка компонента в поверхневому шарі Хімічний потенціал у поверхневому шарі відрізняється від хімічного потенціалу в об'ємі на величину роботи утворення поверхні:

Рівновага між поверхневим шаром та об'ємом для багатокомпонентної гомогенної конденсованої системи xi – мольна частка компонента в об'ємі; yi – мольна частка компонента в поверхневому шарі Вираз для поверхневої енергії гомогенної конденсованої фази Міняємо знаки

Рівновага між поверхневим шаром та об'ємом для багатокомпонентної гомогенної конденсованої системи Двокомпонентна система з частинками, що не дуже відрізняються за розмірами (1 = 2 =  та A1 = A2 = A)

Рівновага між поверхневим шаром та об'ємом для багатокомпонентної гомогенної конденсованої системи

Рівновага між поверхневим шаром та об'ємом для багатокомпонентної гомогенної конденсованої системи

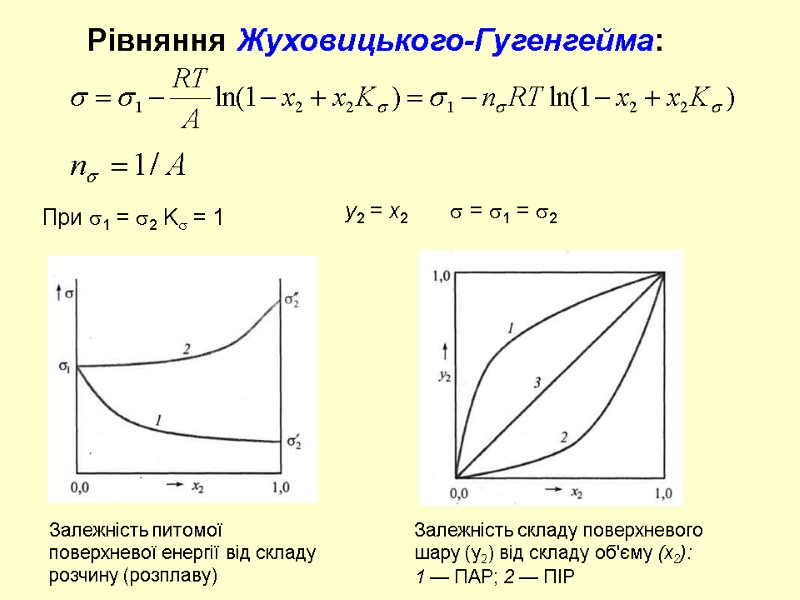
Рівняння Жуховицького-Гугенгейма: При 1 = 2 K = 1 y2 = x2  = 1 = 2 Залежність питомої поверхневої енергії від складу розчину (розплаву) Залежність складу поверхневого шару (у2) від складу об'єму (х2): 1 — ПАР; 2 — ПІР

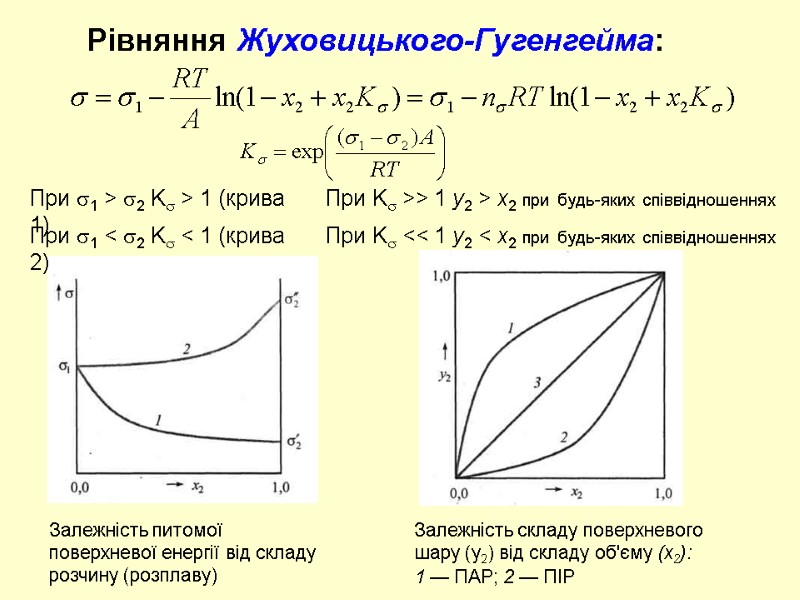
Рівняння Жуховицького-Гугенгейма: При 1 > 2 K > 1 (крива 1) Залежність питомої поверхневої енергії від складу розчину (розплаву) Залежність складу поверхневого шару (у2) від складу об'єму (х2): 1 — ПАР; 2 — ПІР При K >> 1 y2 > x2 при будь-яких співвідношеннях При 1 < 2 K < 1 (крива 2) При K << 1 y2 < x2 при будь-яких співвідношеннях

При K << 1 Рівняння Жуховицького-Гугенгейма: При малих x2 Критерій Жуховицького для ПАР

Рівняння для ПАР у розведених розчинах Рівняння Ленгмюра для адсорбції: Рівняння Шишковського для поверхневого натягу:

Поверхнева енергія твердих тіл Для монокристалів  є анізотропною величиною Для кубічної гранецентрованої гратки: Для кубічної об’ємноцентрованої гратки:

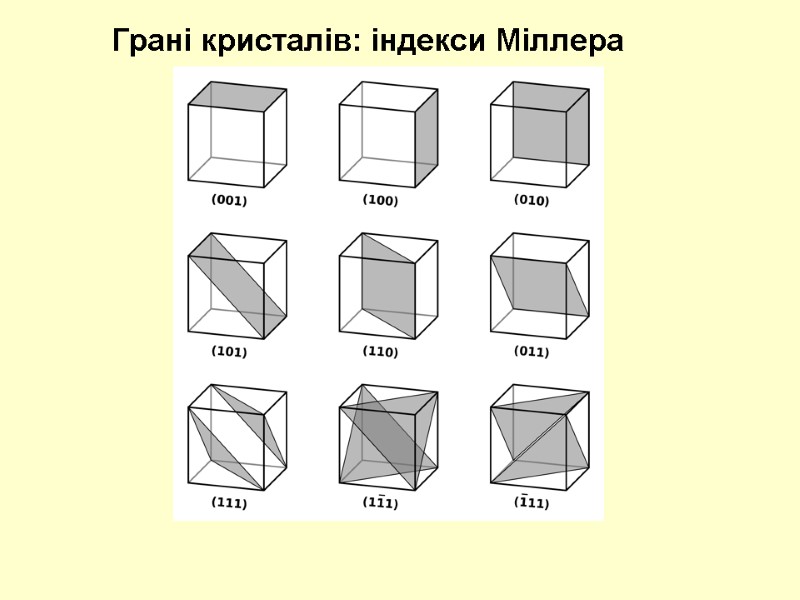
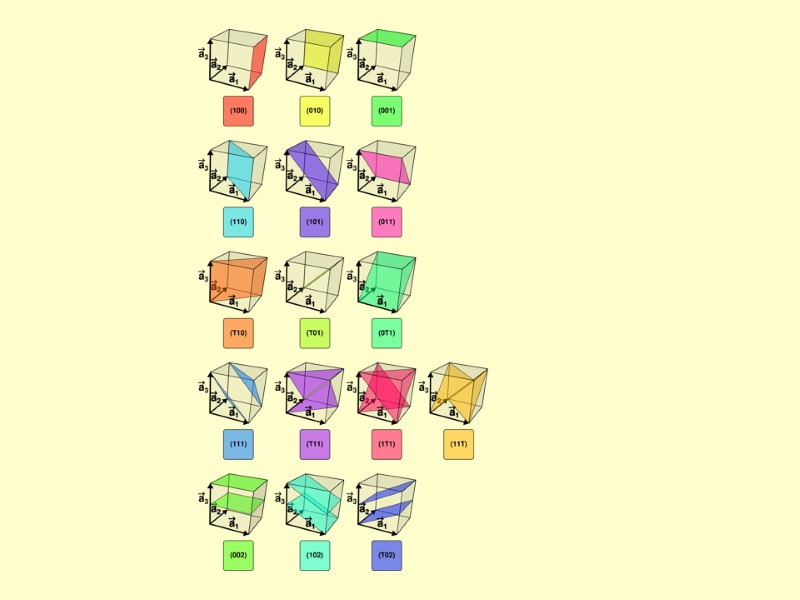
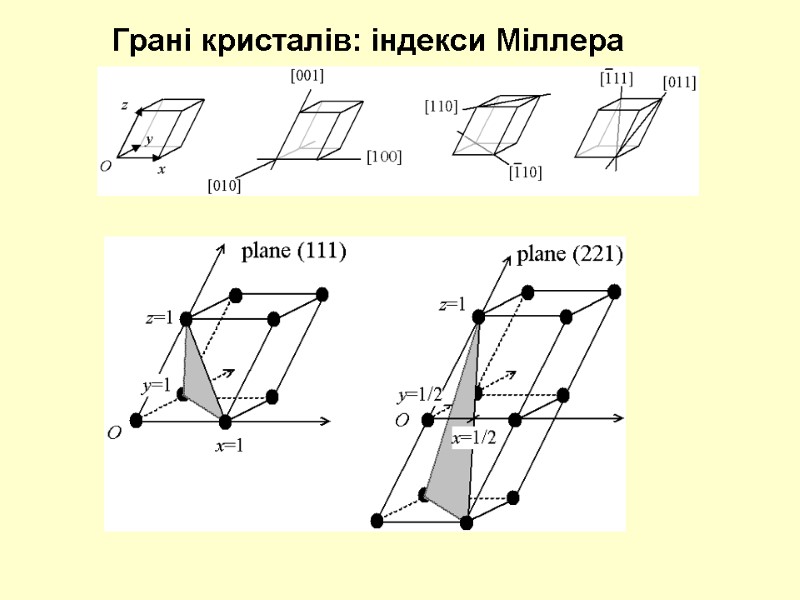
Грані кристалів: індекси Міллера

Грані кристалів: індекси Міллера

Принцип мінімуму вільної енергії Гіббса-Кюрі для монокристалів i - поверхнева енергія i-ї грані, Si – її площина при

Теорема Вульфа hi - висота перпендикуляру, що опущений з центру кристалізації на i-ту грань монокристала Грані з малими значеннями i розташовані у безпосередній близькості до центрів кристалізації і отримують максимальний розвиток.

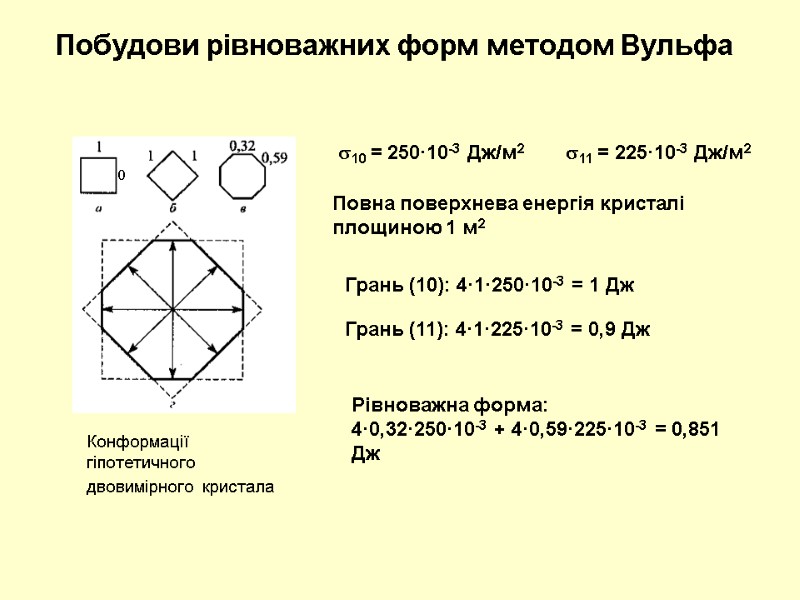
Конформації гіпотетичного двовимірного кристала Побудови рівноважних форм методом Вульфа 10 = 250·10-3 Дж/м2 11 = 225·10-3 Дж/м2 Повна поверхнева енергія кристалі площиною 1 м2 Грань (10): 4·1·250·10-3 = 1 Дж 0 Грань (11): 4·1·225·10-3 = 0,9 Дж Рівноважна форма: 4·0,32·250·10-3 + 4·0,59·225·10-3 = 0,851 Дж

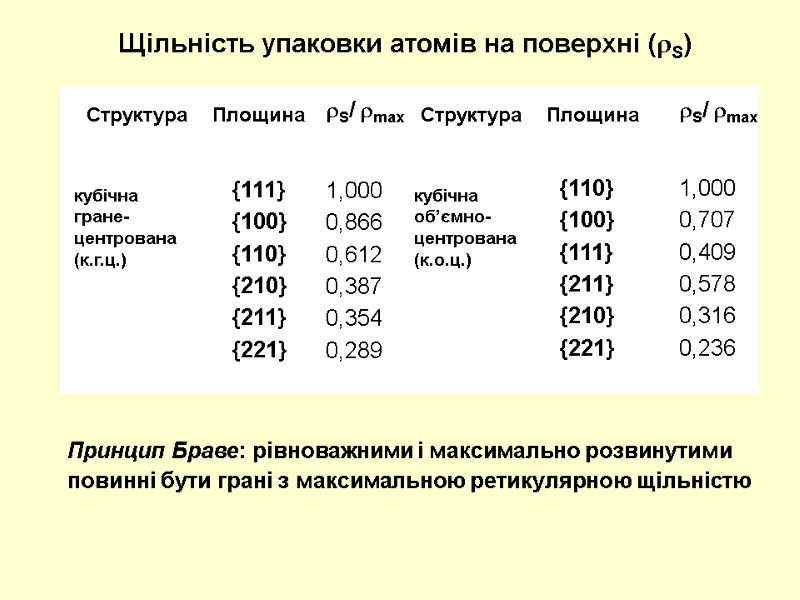
Щільність упаковки атомів на поверхні (S) Структура Площина Структура Площина S/ max S/ max кубічна гране-центрована (к.г.ц.) кубічна об’ємно-центрована (к.о.ц.) {111} {100} {110} {210} {211} {221} {110} {100} {111} {211} {210} {221} 1,000 0,866 0,612 0,387 0,354 0,289 1,000 0,707 0,409 0,578 0,316 0,236 Принцип Браве: рівноважними і максимально розвинутими повинні бути грані з максимальною ретикулярною щільністю