ФИЗИЧЕСКИЕ ОСНОВЫ ПРОИЗВОДСТВА Третий семестр Лекции : 17

ФИЗИЧЕСКИЕ ОСНОВЫ ПРОИЗВОДСТВА Третий семестр Лекции : 17 часов Упражнения :34 часа

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА ОСНОВНАЯ 1.Савельев И.В. Курс общей физики. Книга 3. Молекулярная физика и термодинамика. М.:Издательство АСТ. 2007.-208с. 2. Бокштейн Б.С., Менделев М.И. Краткий курс физической химии. М.: Издательство ЧеРо.2001.-232с. 3.Пономарева К.С.,Гугля В.Г.,Никольский Г.С. Сборник задач по физической Химии. М.: МИСиС.2007.-340с. 4.Падерин С.Н.,Серов Г.В.,Рыжонков Д.И. Теория гомогенных и гетерогенных Процессов. М.:МИСиС.2003.-164с. ДОПОЛНИТЕЛЬНАЯ 1. Падерин С.Н.,Серов Г.В, Рыжонков Д.И. Термодинамика, кинетика и Расчеты металлургических процессов (на английском языке). М.: издательский Дом МИСиС.2010.-235с.

ОСНОВЫ МОЛЕКУЛЯРНОЙ ФИЗИКИ И ТЕРМОДИНАМИКИ МОЛЕКУЛЯРНАЯ ФИЗИКА - РАЗДЕЛ ФИЗИКИ, ИЗУЧАЮЩИЙ СТРОЕНИЕ И СВОЙСТВА ВЕЩЕСТВА. Представляют, что любое вещество(или физическое тело) состоит из мельчайших частиц – атомов, молекул. Это касается веществ или тел, находящихся в твердом, жидком или газообразном состоянии. Полагают, что молекулы вещества находятся в беспорядочном, хаотичном движении. Интенсивность этого движения зависит от температуры. МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ ВЕЩЕСТВА – ОСНОВЫВАЕТСЯ НА ПОЗИЦИИ АТОМИЗМА: МАКРОСКОПИЧЕСКИЕ ФИЗИЧЕСКИЕ ТЕЛА – ТЕЛА, СОСТОЯЩИЕ ИЗ ОЧЕНЬ БОЛЬШОГО ЧИСЛА АТОМОВ ИЛИ МОЛЕКУЛ ЛЕКЦИЯ 1

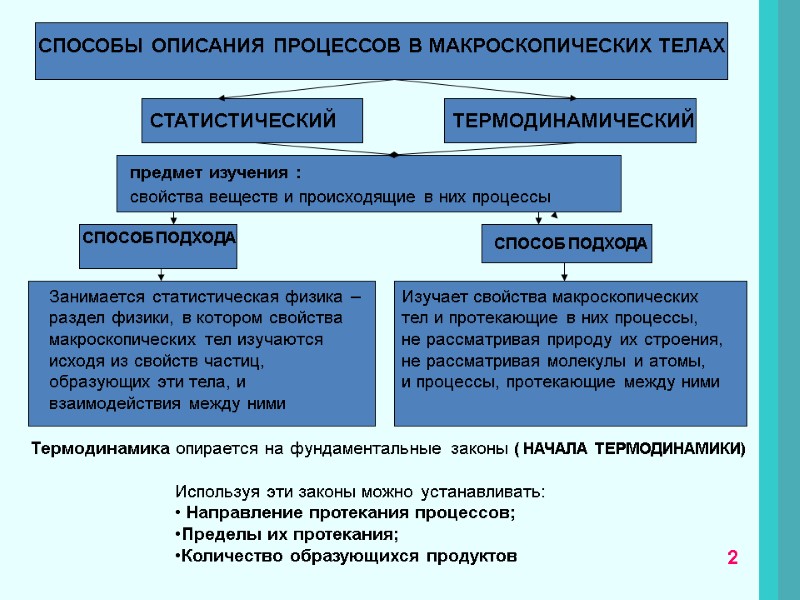
СПОСОБЫ ОПИСАНИЯ ПРОЦЕССОВ В МАКРОСКОПИЧЕСКИХ ТЕЛАХ Занимается статистическая физика – раздел физики, в котором свойства макроскопических тел изучаются исходя из свойств частиц, образующих эти тела, и взаимодействия между ними Изучает свойства макроскопических тел и протекающие в них процессы, не рассматривая природу их строения, не рассматривая молекулы и атомы, и процессы, протекающие между ними СТАТИСТИЧЕСКИЙ ТЕРМОДИНАМИЧЕСКИЙ Термодинамика опирается на фундаментальные законы ( НАЧАЛА ТЕРМОДИНАМИКИ) предмет изучения : свойства веществ и происходящие в них процессы СПОСОБ ПОДХОДА СПОСОБ ПОДХОДА СПОСОБ ПОДХОДА Используя эти законы можно устанавливать: Направление протекания процессов; Пределы их протекания; Количество образующихся продуктов 2

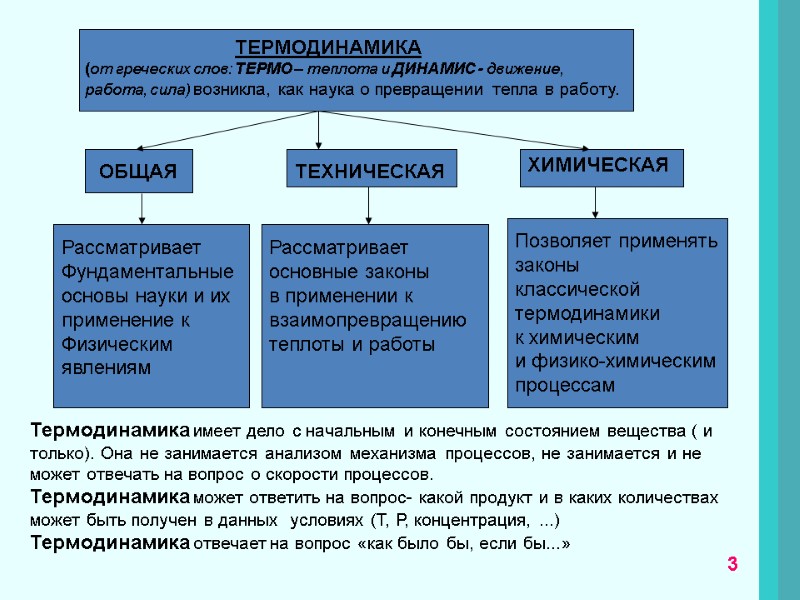
ТЕРМОДИНАМИКА (от греческих слов: ТЕРМО – теплота и ДИНАМИС - движение, работа, сила) возникла, как наука о превращении тепла в работу. ОБЩАЯ ТЕХНИЧЕСКАЯ ХИМИЧЕСКАЯ Рассматривает Фундаментальные основы науки и их применение к Физическим явлениям Рассматривает основные законы в применении к взаимопревращению теплоты и работы Позволяет применять законы классической термодинамики к химическим и физико-химическим процессам Термодинамика имеет дело с начальным и конечным состоянием вещества ( и только). Она не занимается анализом механизма процессов, не занимается и не может отвечать на вопрос о скорости процессов. Термодинамика может ответить на вопрос- какой продукт и в каких количествах может быть получен в данных условиях (T, Р, концентрация, ...) Термодинамика отвечает на вопрос «как было бы, если бы...» 3

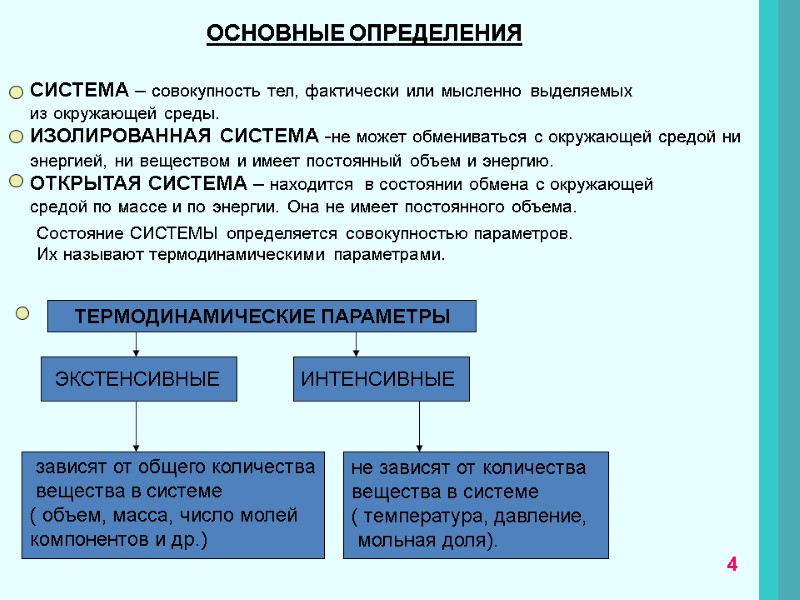
ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ СИСТЕМА – совокупность тел, фактически или мысленно выделяемых из окружающей среды. ИЗОЛИРОВАННАЯ СИСТЕМА -не может обмениваться с окружающей средой ни энергией, ни веществом и имеет постоянный объем и энергию. ОТКРЫТАЯ СИСТЕМА – находится в состоянии обмена с окружающей средой по массе и по энергии. Она не имеет постоянного объема. Состояние СИСТЕМЫ определяется совокупностью параметров. Их называют термодинамическими параметрами. ТЕРМОДИНАМИЧЕСКИЕ ПАРАМЕТРЫ зависят от общего количества вещества в системе ( объем, масса, число молей компонентов и др.) ЭКСТЕНСИВНЫЕ ИНТЕНСИВНЫЕ не зависят от количества вещества в системе ( температура, давление, мольная доля). 4

КОМПОНЕНТ – химически индивидуальное вещество, которое может быть выделено из системы и существовать самостоятельно. (Для характеристики системы не обязательно знать все параметры, можно ограничиться лишь некоторыми). ПАРАМЕТРЫ, которые выбирают в качестве независимых переменных и которые определяют состояние системы, называют параметрами состояния системы. (Обычно это такие параметры, величину которых можно измерить: температура, объем, давление, концентрация.) Окружающая среда, как и сама система, обладает также определенными свойствами и характеризуется параметрами. Эти параметры по отношению к системе будут внешними, обычно это температура и давление. СОСТОЯНИЕ СИСТЕМЫ НАЗЫВАЕТСЯ РАВНОВЕСНЫМ, если все параметры состояния имеют определенные значения и не изменяются во времени. СОСТОЯНИЕ СИСТЕМЫ ЯВЛЯЕТСЯ НЕРАВНОВЕСНЫМ, если хотя бы один из параметров не имеет определенного значения. ТЕРМОДИНАМИЧЕСКИЙ ПРОЦЕСС – есть переход системы из одного состояния равновесия в другое. Этому соответствует изменение одного или нескольких параметров системы. РАВНОВЕСНЫЙ ПРОЦЕСС представляется состоящим из бесконечно большого числа последовательных равновесных состояний при условии, что протекает бесконечно медленно. 5

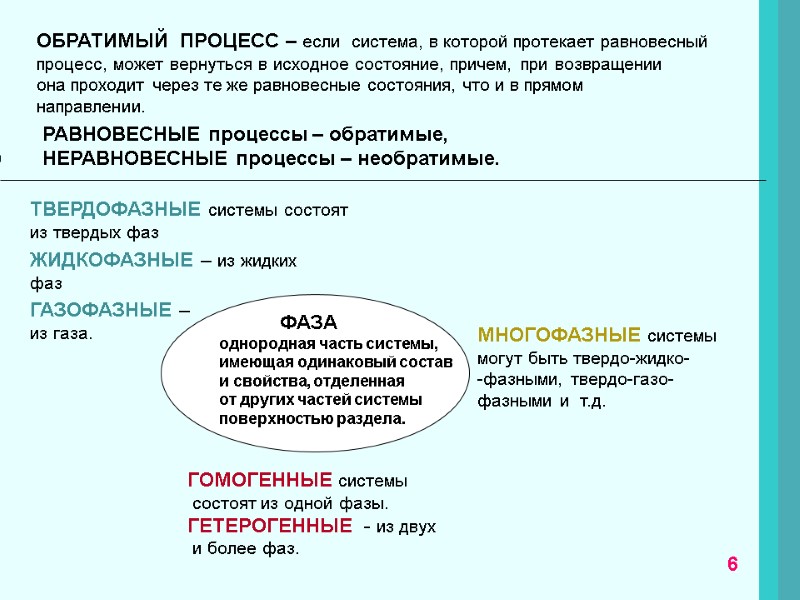
ОБРАТИМЫЙ ПРОЦЕСС – если система, в которой протекает равновесный процесс, может вернуться в исходное состояние, причем, при возвращении она проходит через те же равновесные состояния, что и в прямом направлении. РАВНОВЕСНЫЕ процессы – обратимые, НЕРАВНОВЕСНЫЕ процессы – необратимые. ФАЗА однородная часть системы, имеющая одинаковый состав и свойства, отделенная от других частей системы поверхностью раздела. ТВЕРДОФАЗНЫЕ системы состоят из твердых фаз ЖИДКОФАЗНЫЕ – из жидких фаз ГАЗОФАЗНЫЕ – из газа. МНОГОФАЗНЫЕ системы могут быть твердо-жидко- -фазными, твердо-газо-фазными и т.д. ГОМОГЕННЫЕ системы состоят из одной фазы. ГЕТЕРОГЕННЫЕ - из двух и более фаз. 6

ИЗОБАРИЧЕСКИЙ процесс протекает при ИЗОХОРИЧЕСКИЙ процесс протекает при ЭКЗОТЕРМИЧЕСКИЙ процесс протекает с выделением тепла. ЭНДОТЕРМИЧЕСКИЙ процесс протекает с поглощением тепла. Равновесная термодинамика - (термодинамика равновесных процессов) рассматривает лишь равновесные и обратимые процессы. Реальные процессы не являются равновесными и обратимыми. Сведения, полученные для равновесных обратимых процессов путем использования дополнительных коэффициентов, распространяются на реальные процессы. МОЛЬ-количество вещества, содержащее столько структурных единиц (частиц-молекул, атомов), сколько атомов содержится в 12 г углерода Число атомов в 12 г углерода – постоянная Авогадро ИЗОТЕРМИЧЕСКИЙ процесс – протекает при 7

ИДЕАЛЬНЫЕ ГАЗЫ Модель идеального газа 1.Молекулы (атомы)принимаются за материальные точки с определенной массой. Размеры их ничтожны по сравнению с расстоянием между ними. 2.Молекулы(атомы) находятся в состоянии непрерывного и постоянного движения. Между столкновениями они движутся прямолинейно. Движения равновероятны по всем направлениям. 3.Скорости частиц могут быть любыми. 4.При столкновении молекулы (атомы)ведут себя как упругие шары. Между частицами не действуют силы притяжения или отталкивания

В газах простейшими частицами являются молекулы ... , т.е. электронейтральные частицы, состоящие из двух- трех и более атомов. Инертные газы и металлы в парах одноатомны: При нормальных условиях (P=1 атм, ) средние расстояния между молекулами намного больше радиуса действия сил межмолекулярного взаимодействия. При нормальных условиях в газа находится молекул и среднее расстояние между ними составляет около 10 нм, тогда как межмолекулярное взаимодействие становятся несущественным уже на расстоянии свыше 0,5-1,0 нм, т.е. радиус межмолекулярного взаимодействия меньше расстояния между частицами более чем в 10 раз. Объем самих молекул составляет от объема газа. Это позволяет считать собственный объем молекул пренебрежительно малым и рассматривать молекулы как материальные точки. Газ, молекулы которого рассматриваются как невзаимодействующие друг с другом материальные точки, называется ИДЕАЛЬНЫМ 8

УРАВНЕНИЯ СОСТОЯНИЙ ИДЕАЛЬНОГО ГАЗА Соотношения, связывающие параметры состояний тела называются уравнениями состояний этого тела. Эмпирически установлено, что параметры состояния кислорода и азота при обычных условиях (t ~ 20 ºC, P~1 aтм) подчиняются уравнению (1) b-const, пропорциональная массе газа. УРАВНЕНИЕ ИДЕАЛЬНОГО ГАЗА -молярный объем, R- молярная газовая постоянная Чем меньше плотность газа, тем точнее выполняется это уравнение. Наиболее точно этому уравнению подчиняется идеальный газ. Близкими по свойствам к идеальному газу является гелий и водород. По закону Авогадро при нормальных условиях, т.е. при t = 0 ºC, (273,15К) и P=1 aтм (1,013 105 ), 1 моль любого газа занимает объем 22,4 литра ( ) ). Отсюда, для одного моля любого газа константа b будет одинакова. Обозначив «b» для одного моля газа «R» запишем уравнение состояния идеального газа в виде: (2) 9

УРАВНЕНИЕ ДЛЯ ПРОИЗВОЛЬНОЙ МАССЫ m ИДЕАЛЬНОГО ГАЗА M- молярная масса газа (3) Для одинаковых P и T газ, массой m будет занимать объем в Z больший, чем , потому . Тогда - уравнение состояния для массы m идеального газа. (4) Умножим и разделим правую часть уравнения (4) на -число Авогадро (5) - число молекул, содержащихся в массе m газа. [ – постоянная Больцмана Уравнения (1), (2), (3), (4), (6) – различные формы записи уравнения состояния идеального газа. Плотность газа , из (4) ] Отсюда (6) 10

РЕАЛЬНЫЕ ГАЗЫ При повышении плотности изменяются свойства газов – они перестают быть идеальными. Простейшим уравнением, которое качественно правильно описывает отличие реального газа от идеального, является уравнение Ван-дер-Ваальса (7) константы, определяемые экспериментально. Характеризуют отклонение реального газа от идеального. - имеет размерность давления и учитывает притяжение молекул в результате межмолекулярного взаимодействия. b - поправка на собственный объем молекул, учитывающая отталкивание молекул на близком расстоянии. Уравнение Ван-дер-Ваальса не является универсальным, т.к.параметры для разных газов различны. К теоретически обоснованным относится вириальное уравнение состояния: - вириальные коэффициенты. (8) Уравнение дает достаточно полное описание свойств газа ПЛОТНОГО, если использовать большое число членов. 11

СРАВНЕНИЕ РЕЗУЛЬТАТОВ ОПИСАНИЯ СВОЙСТВ АЗОТА ПО УРАВНЕНИЯМ ИДЕАЛЬНОГО ГАЗА И ВАН-ДЕР-ВААЛЬСА (при различных давлениях, ) 12 ,V=1л В технологических процессах давление газовых атмосфер часто составляет 1атм и обычно не превышает 10-15атм, потому реальные газы можно описывать уравнениями идеального. При больших объемах и низких давлениях уравнение Ван-Дер-Ваальса. переходит в уравнение идеального газа

Общее давление смеси идеальных газов равно сумме парциальных давлений компонентов. Парциальное давление компонентов в смеси, это давление, которое он оказывает, занимая весь тот объем, что и смесь, при той же температуре. Вторая форма записи закона: -молярная доля го компонента в смеси. ЗАКОН ДАЛЬТОНА (9) 13

ЗАКОНЫ ТЕРМОДИНАМИКИ 1. НУЛЕВОЙ ЗАКОН ТЕРМОДИНАМИКИ (Определяет условие равновесного состояния системы.) Формулировки: Если каждая из двух систем находятся в тепловом равновесии с третьей, то эти две системы также находятся в тепловом равновесии Определенная фиксированная температура системы возможна лишь для состояния равновесия (или, если температура во всех частях системы одна и та же, то система находится в состоянии равновесия) Нулевой закон лежит в основе измерения температуры с помощью термометров. Из нулевого закона термодинамики следует вывод об АДДИТИВНОСТИ (возможности суммирования термодинамических свойств) АДДИТИВНОСТЬ означает, что какая-либо величина, характеризующая свойства системы в целом, равна сумме этих величин отдельных частей системы, независимо от того, каким образом система разбивается на части. Энергия всей системы, находящейся в равновесии равна сумме энергий ее составных частей. Это касается и аддитивности термодинамических функций состояния в условиях равновесия. 14

Теплота и работа – два способа передачи энергии. Теплота –форма передачи энергии путем столкновения молекул соприкасающихся тел, т.е. путем теплообмена. Направление передачи теплоты определяется температурой. Работа, совершаемая системой, определяется взаимодействием системы с внешней средой, в результате которого преодолеваются внешние силы, нарушавшие равновесие в системе. Для того, чтобы система совершила работу, необходимо наличие внешних сил. ТЕПЛОТА, РАБОТА, ФУНКЦИИ СОСТОЯНИЯ Функции состояния зависят только от состояния системы, но не зависят от того, каким образом система попала в это состояние. 15 Функции состояния: внутренняя энергия (U), энтальпия (H), энтропия (S), - функция состояния. Переход системы из состояния 1 в состояния 2 может быть осуществлен разными путями: а, б, в. - изменение функции состояния системы при переходе из положения 1 в положение 2 зависит только от конечного и начального состояний и не зависит от пути перехода.

ВНУТРЕННЯЯ ЭНЕРГИЯ Так, внутренняя энергия U тела складывается из кинетической энергии движущихся молекул и потенциальной энергии, т.е. энергии взаимного притяжения и отталкивания частиц (молекул). Во внутреннюю энергию также входят: энергия электронов, ядерная энергия и т.д. Внутренняя энергия U системы (тела) должна зависеть от температуры Т (кинетическая энергия молекул) и от объема V , так как потенциальная энергия – энергия взаимного притяжения и отталкивания, зависит от расстояния между молекулами. Потому Характеризует общий запас энергии системы, включает все виды движения и взаимодействия частиц, составляющих систему. 16

17 СВОЙСТВА ВНУТРЕННЕЙ ЭНЕРГИИ 1. Внутренняя энергия не может равняться нулю (нет веществ без движения). Она всегда положительна и тем больше, чем больше движение. 2. Внутренняя энергия изолированной системы всегда остается постоянной величиной, независимо от протекающих в системе процессов. 3. Внутренняя энергия складывается из отдельных видов энергии, которые превращаются друг в друга в строго эквивалентных количествах. 4. Внутренняя энергия является однозначной функцией состояния системы, т.е. каждому состоянию системы соответствует одно значение внутренней энергии. Абсолютное значение внутренней энергии системы определить невозможно, но в термодинамике это и не нужно. Достаточно знать изменение внутренней энергии при переходе системы из одного состояния в другое.

18 ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ (Это есть закон сохранения и превращения энергии в применении процесса, связанного с превращением теплоты и работы.) Теплота Q, сообщаемая системе, идет на превращение внутренней энергии и на работу A, совершаемую системой. Для процесса, в котором происходит бесконечно малое изменение, -полный дифференциал внутренней энергии системы -бесконечно малые изменения теплоты и работы. Поскольку работа представляет собой одну из форм передачи энергии, то из первого закона следует постулат о невозможности создания двигателя, работающего без затраты энергии. ВЕЧНЫЙ ДВИГАТЕЛЬ ПЕРВОГО РОДА НЕВОЗМОЖЕН. В изолированной системе Из первого закона термодинамики следует: . Внутренняя энергия изолированной системы величина постоянная. ЛЕКЦИЯ 2

19 ЭНТАЛЬПИЯ В химических и физико-химических процессах передача теплоты часто происходит при постоянном давлении . Много промышленных агрегатов, в т.ч. в металлургии, представляют собой открытые системы, работающие при 1 атм. Большее практическое значение по сравнению с внутренней энергией имеет другая функция состояния – энтальпия. ЭНТАЛЬПИЯ системы (Н) – есть величина, равная сумме внутренней энергии (U) и потенциальной энергии всестороннего сжатия (PV) По физическому смыслу Н – полная энергия системы. ИЗМЕНЕНИЕ ЭНТАЛЬПИИ ПРИ

20 Значения различаются существенно для газов. Для жидкостей и твердых тел, для которых объем V при изменении температуры Т меняется незначительно, это различие несущественно. Если , это означает, что теплосодержание системы повысилось в ходе процесса, т.е. тепло поглощается ( процесс эндотермический). Если , то теплосодержание системы понизилось в ходе процесса,т.е. тепло выделяется ( процесс экзотермический). Выделяющееся или поглощаемое тепло в ходе химической реакции называют тепловым эффектом реакции. Тепловой эффект процесса при равен , а при равен .

21 ТЕПЛОЕМКОСТЬ Под теплоемкостью тела понимают количество теплоты, которое нужно сообщить телу, чтобы повысить его температуру на один Кельвин(при отсутствии химических реакций и фазовых превращений). Молярная теплоемкость (С) – количество теплоты, необходимое для нагревания одного моля вещества на 1К (Дж/моль К). Удельная теплоемкость (с) – количество теплоты, необходимое для нагревания единицы массы вещества на 1К (Дж/г К) с=С/М, где М –молярная масса. Средняя теплоемкость – отношение количества теплоты, подводимой к телу, к интервалу температур, в пределах которого нагревается (или охлаждается ) тело. (Дж/моль К) Истинная теплоемкость соответствует бесконечно малому изменению температуры

В зависимости от условий, при которых происходит нагревание, различают - теплоемкость при постоянном объеме - теплоемкость при постоянном давлении Зависимость теплоемкости от температуры имеет вид Связь между истинной и средней теплоемкостью Теплоемкости (изохорная ) и (изобарная ) выражаются через частные производные от функции состояния U и H постоянные 22

23 (При протекании химической реакции происходит выделение или поглощение тепла. Это тепло называют тепловым эффектом реакции. Тепловой эффект при характеризует изменение внутренней энергии , а при - изменение энтальпии . Температуры исходных веществ и продуктов должны быть одинаковы.) -Тепловой эффект реакции при или является функцией состояния (зависит только от начального и конечного состояния системы) и не зависит от пути перехода от исходного состояния к конечному. -Тепловой эффект реакции определяется только природой и состоянием исходных веществ и продуктов реакции, то есть не зависит от промежуточных химических реакций Практическое значение закона: на его основании для вычисления термодинамических функций, в т.ч. тепловых эффектов реакций, можно использовать другие реакции, для которых данные функции известны. Уравнения реакций можно алгебраически складывать, чтобы получить нужное уравнение, то же самое делать и с термодинамическими функциями. ТЕРМОХИМИЯ. ЗАКОН ГЕССА

24 ПРИМЕР Применение закона Гесса будет правильным, если во всех используемых реакциях будут одинаковы начальные и конечные условия существования веществ ( прежде всего, температуры и давления).

СТАНДАРТНОЕ СОСТОЯНИЕ ВЕЩЕСТВА Для удобства сопоставления тепловых эффектов, других термодинамических функций вводится представление о стандартном состоянии вещества. Для твердых и жидких веществ в качестве стандартных принимаются их устойчивые состояния в природе при давлении Па. Для газов – состояние идеального газа при Па. ПРИМЕР: Для ртути принимается жидкое состояние, для кислорода – газообразное, для углерода принимается графит, для йода – твердое состояние и т.д. Стандартные состояния могут выбираться при любых температурах. В справочных изданиях приводят значения термодинамических функций при Па и температуре Все величины, относящиеся к стандартному состоянию веществ отмечают индексом «о». (298,15 К). 25

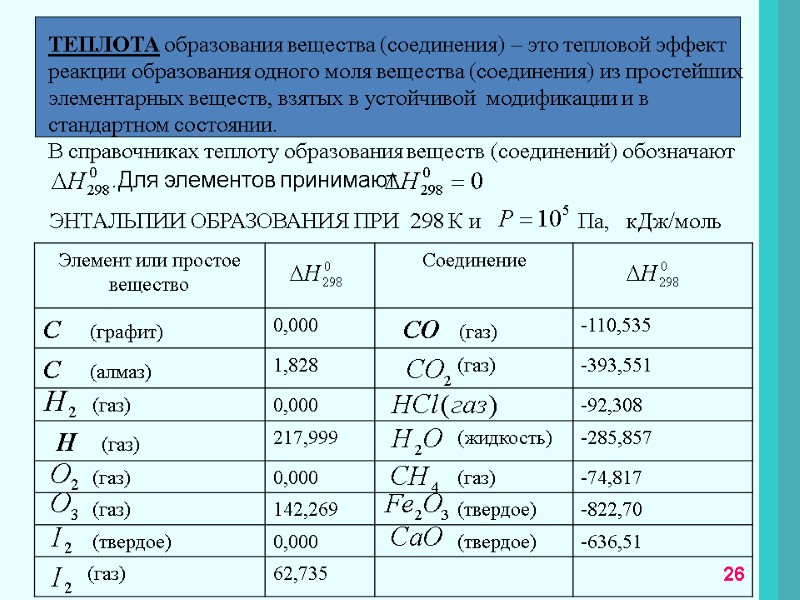
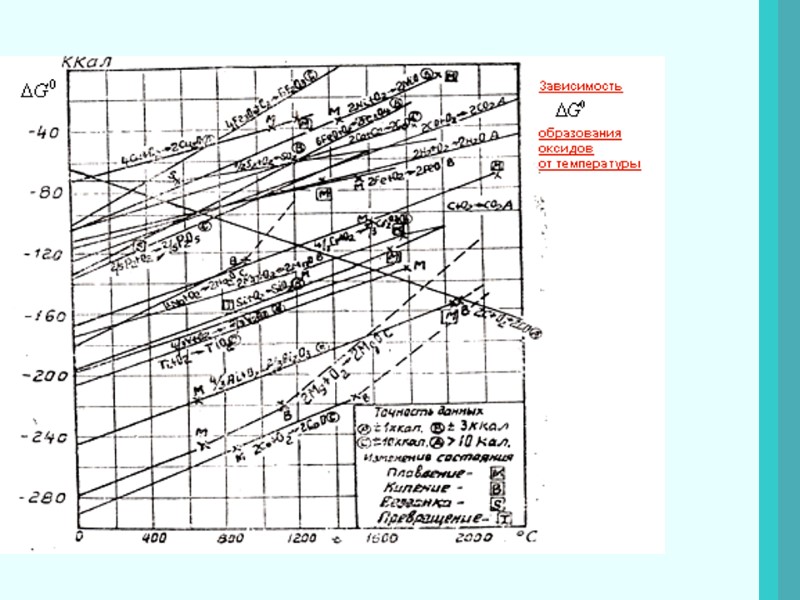
ТЕПЛОТА образования вещества (соединения) – это тепловой эффект реакции образования одного моля вещества (соединения) из простейших элементарных веществ, взятых в устойчивой модификации и в стандартном состоянии. В справочниках теплоту образования веществ (соединений) обозначают .Для элементов принимают ЭНТАЛЬПИИ ОБРАЗОВАНИЯ ПРИ 298 К и Па, кДж/моль 26

27 В 1975 году ИЮПАК рекомендовала принять, что энтальпии образования всех элементов в их стандартных состояниях равны нулю при любой температуре. Тепловой эффект реакции равен разности между теплотами образования продуктов реакции , т.е. веществ в правой части уравнения, и теплотами образования исходных веществ, т.е. стоящих в левой части уравнения. Величины теплот образования умножаются при этом на коэффициенты, равные стехиометрическим коэффициентам уравнения. исх.в-в ПРИМЕР

28 ЗАВИСИМОСТЬ ТЕПЛОВОГО ЭФФЕКТА РЕАКЦИИ ОТ ТЕМПЕРАТУРЫ Ранее было показано и , тогда и Эти выражения представляют закон Кирхгоффа в дифференциальной форме. В интегральной форме: ; или , где изменение изобарной теплоемкости системы при переходе из состояния 1 ( ) в состояние 2 ( т.е. разность теплоемкостей продуктов и исходных веществ с учетом стехиометрических коэффициентов. ) ,

29 Для нахождения теплового эффекта при температуре необходимо знать его величину при какой-либо другой температуре. Например, стандартной, т.е. при 298 К. Если при изменении температуры , то В общем виде зависимость теплоемкости от температуры имеет вид а, в, с – постоянные, характеризующие рассматриваемое вещество или элемент. Число членов в уравнении зависит от требуемой степени точности и величины температурного материала. Коэффициенты приведены в справочных таблицах ПРИМЕР: Для водяного пара В интервале температур 300-2500 К

ВТОРОЙ ЗАКОН ТЕРМОДИНАМИКИ 30 Первый закон термодинамики позволяет рассчитывать балансы тепловых процессов, но не может предсказать направления их протекания. Процессы, наблюдаемые в природе, протекают самопроизвольно (сами собой) только в одном направлении – в сторону достижения равновесия и прекращаются, когда это состояние достигается. Существуют разные формулировки второго закона термодинамики. Теплота не может самопроизвольно переходить от более холодного тела к более нагретому. «Вечный двигатель 2-го рода» невозможен. (под вечным двигателем второго рода Понимается машина, которая могла бы превращать всю подводимую к ней теплоту в работу. Такая машина имела бы КПД равным 1). В изолированных системах самопроизвольно идут процессы только с возрастанием энтропии и до такого состояния, при котором энтропия максимальна для данных условий. ЭНТРОПИЯ Энтропия (S) –одна из основных термодинамических функций состояния. При переходе системы из одного состояния в другое энтропию можно вычислить на основании статистических законов. Второй закон термодинамики, в отличие от первого, имеет статистический характер и не применим для систем из малого числа частиц, ( молекул, атомов, ионов и др.).

Беспорядок (колебательный, поступательный, конфигурационный) - физическое свойство вещества; оно также неотделимо, как и движение. Энтропия системы или вещества – есть мера всех видов беспорядков 31 Нельзя, например, говорить об энтропии одной молекулы. В этом случае исчезает различие между порядком и беспорядком, а понятие о самопроизвольном и равновесном процессах теряет смысл. Второй закон термодинамики имеет дело только со множеством частиц. Температура, концентрация, плотность, давление определяются из беспорядочного движения множества частиц. Эти параметры являются некими средними величинами, основанными на результате действия большого числа частиц и теряют смысл при приложении их к отдельным частицам. Тело, состоящее из большого количества молекул можно рассматривать с микроскопической и макроскопической точек зрения.

32 В первом случае следим за поведением каждой молекулы. Во втором – рассматриваем суммарный результат по общим для данного тела характеристикам:V, и т.д. В этом случае рассматриваемое тело представляет макросистему. Макросистема и будет термодинамическим состоянием. Оно определяется Т, Р, концентрацией и т.д. и отличается от микросостояния, задаваемого положением, скоростью и направлением движения каждой отдельной частицы. Одна и та же макросистема может существовать при различном расположении и различной энергии отдельных частиц, определяющих микросостояние системы. Число микросостояний, с помощью которых может быть осуществлено данное макросостояние, называется термодинамической вероятностью (W).

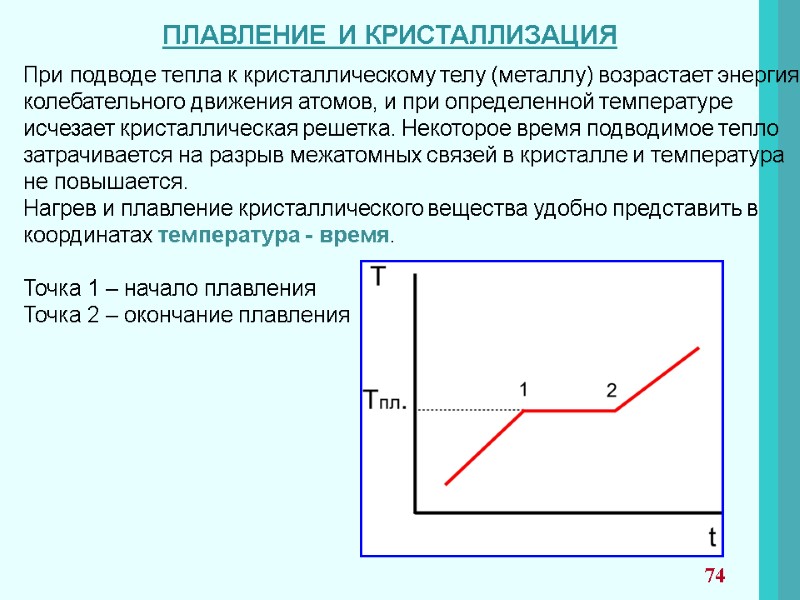
33 ФОРМУЛА БОЛЬЦМАНА Дж/К 1/моль Реальный физический смысл энтропии: она является мерой вероятности термодинамического состояния тел и систем. При создании системы из двух систем с вероятностями , ее вероятность равна произведению . Отсюда Поскольку энтропия - функция состояния, она может быть представлена в виде функции параметров состояния Р, V, Т и т.д., ее можно связать с теплотой обратимого процесса. В этом случае энтропия – функция состояния, приращение которой в ходе обратимого процесса равно отношению элементарного количества полученной системой теплоты к термодинамической температуре системы.

34 Для необратимых процессов Для общего случая обратимых и необратимых процессов можно объединить в соотношения: . Эти соотношения лежат в основе применения энтропии в термодинамике. Изменение энтропии может ответить на вопрос о возможности самопроизвольного процесса. , т.к. ИЗОЛИРОВАННАЯ СИСТЕМА Если процесс возможен, если - нет. Всякий самопроизвольный (необратимый) процесс в изолированной системе связан с увеличением энтропии. Для неизолированных систем величина может быть положительной, отрицательной или равной нулю и не может служить критерием для определения возможности самопроизвольного процесса.

35 Все реальные системы неизолированные, подавляющее большинство из них являются открытыми. Для таких систем только с помощью энтропии нельзя оценить направление процесса. Вводятся еще две термодинамические функции состояния - энергия Гельмгольца(А) и энергия Гиббса(G), с их помощью появляется возможность определять условия самопроизвольных и равновесных процессов в неизолированных системах. или или Поясним смысл приведенных уравнений и их правых частей. Предположим, что система имеет температуру Т, а температура окружающей среды ,причем . . Система остывает и отдает тепло окружающей среде, равное dU при V=const, и равное dH при P=const, ее конечная температура- . В этих условиях система сообщает внешней среде только часть своей внутренней энергии, которую называют свободной энергией. СВОБОДНАЯ ЭНЕРГИЯ

36 В изобарно-изотермических условиях она выступает в форме энергии Гиббса, в изохорно-изотермических- энергии Гельмгольца. Таким образом, энергия Гиббса (энергия Гельмгольца)- это часть внутренней энергии, которую система может отдать окружающей среде. Именно поэтому ее называют «свободной». Основная часть внутренней энергии системы, равная теплоте ее нагрева от абсолютного нуля до , остается в системе и не может быть использована вне системы. Эта часть энергии как бы «заперта» в системе , поэтому ее называют связанной энергией. Связанная энергия равна произведению температуры на изменение энтропии , то есть или Итак, энергия Гиббса и энергия Гельмгольца определяют ту часть теплоты (энергии), которую система может отдать. Она равна суммарному запасу энергии системы за вычетом той энергии, которая остается в системе.

37 Величина возрастает по мере объединения частиц, увеличивается при сжатии газа, конденсации пара, затвердевании жидкости, переходе газа в твердое состояние, синтезе молекул из атомов и т.д. Величина ( энтропийный фактор) отражает противоположную тенденцию- стремление частиц к дезинтеграции, переход от порядка к беспорядку, от меньшего беспорядка к большому. К процессам, увеличивающим энтропию, относятся: расширение газа, испарение жидкости, переход твердого тела в газообразное состояние, плавление, растворение и т.д Величина отражает стремление системы к беспорядку при повышении температуры. Случай, когда энтальпийный и энтропийный факторы уравновешивают друг друга, то есть выражает состояние равновесия химических и физико-химических процессов. Если энтропия является критерием направленности самопроизвольного процесса в изолированных системах, то неравенства или характеризуют самопроизвольный процесс в неизолированных системах. Поскольку в реальной жизни физико-химические процессы происходят чаще при P=const, чем при V=const, то значение энергии Гиббса в практических расчетах применяют значительно чаще, чем энергию Гельмгольца.

СТАНДАРТНАЯ ЭНЕРГИЯ ГИББСА СТАНДАРТНОЙ ЭНЕРГИЕЙ ГИББСА соединения называется изменение Энергии ГИББСА реакции образования одного моля соединения из простых веществ при 298 К и давлении Величины стандартных энергий Гиббса образования соединений представлены в термодинамических таблицах. Па С помощью величины можно рассчитывать свободные энергии любых реакций при любых температурах и давлениях. Стандартные энергии Гиббса простых веществ принимаются равными нулю. Например, стандартная энергия Гиббса водяного пара равна -229 кДж/моль. Это означает, что для реакции , проходящей при 298 К и Па, произошло уменьшение на 229 кДж, 38

что свидетельствует о том, что в данных условиях реакция может идти самопроизвольно. Стандартную энергию Гиббса реакции можно рассчитать по стандартным теплотам образования веществ, участвующих в реакции, и по стандартным энтропиям. Тепловой эффект реакции равен: Изменение энтропии реакции: Стандартная энергия Гиббса реакции: 39

ПРИМЕР. Определить стандартную энергию Гиббса при Из справочника находим: кДж/моль; кДж/моль; кДж/моль, тогда: кДж/моль. Результат расчета показывает, что в стандартных условиях данная реакция самопроизвольно может идти только в обратном направлении. 40

ХИМИЧЕСКИЙ ПОТЕНЦИАЛ До сих пор при анализе систем, химических реакций их участники рассматривались как индивидуальные вещества, не влияющие друг на друга. Это позволяло рассчитывать тепловые эффекты реакций, изменения энтропии и свободной энергии. В реальных системах существует взаимное влияние одних участников реакции на свойства других. Химическую реакцию можно рассматривать, как добавка в систему продуктов реакции и удаление исходных веществ. Количество взаимодействующих веществ и продуктов реакции оценивается числом молей (n). В результате реакции изменяются количества молей участников, поэтому изменяется и внутренняя энергия системы и другие функции состояния: Зависимость величин этих функций от числа молей компонентов, характеризует «химический потенциал». Так, частные производные энергии Гиббса по одному из изменяющихся компонентов - i и есть химический потенциал этого компонента - 41

То есть, химический потенциал вещества (компонента) в системе, есть изменение энергии Гиббса системы при увеличении в ней на один моль количества данного вещества, при неизменности Р,Т, постоянстве количества всех остальных компонентов (веществ). Химический потенциал характеризует «скорость» изменения свободной энергии системы при добавлении в систему одного моля i – того компонента. В отличие от других интенсивных параметров системы таких как Р, Т, др. химический потенциал нельзя измерить непосредственно. Частные производные от экстенсивных свойств (V, G, S и др.) по при постоянстве Р, Т и называются парциальными величинами. и является парциальной мольной энергией Гиббса. Таким образом 42

Для однокомпонентной системы вместо приведенного выражения можно записать мольная энергия Гиббса компонента (индивидуального вещества). Па. Тогда Для компонента смеси идеального газа, находящегося в нестандартных условиях, химический потенциал i –го компонента при температуре Т и 298 К соответственно. - парциальное давление компонентов в газовой смеси. Мольную энергию Гиббса можно привести к стандартным условиям: 298 К, 43

ЛЕКЦИЯ 3 ХИМИЧЕСКОЕ РАВНОВЕСИЕ Равновесное состояние в термодинамических процессах характеризуется признаками: Неизменностью равновесного состояния системы при сохранении внешних условий. Устойчивостью равновесия. Это означает самопроизвольное восстановление равновесия после прекращения внешнего воздействия, вызвавшего незначительное отклонение системы от положения равновесия. Динамическим характером равновесия. Равновесие устанавливается и сохраняется вследствие равенства скоростей прямого и обратного процессов. Возможностью подхода к состоянию равновесия с двух противоположных сторон. Минимальным значением в изобарно-изотермических процессах. 44

КОНСТАНТА РАВНОВЕСИЯ Рассмотрим гомогенную газовую реакцию, находящуюся в состоянии равновесия аА + вВ = сС + dD а, в, с, d – стехиометрические коэффициенты. При Т = const в состоянии равновесия между парциальными давлениями компонентов газовой смеси устанавливается постоянное соотношение. Это соотношение является выражением закона действующих масс. Константа равновесия реакции равна: Таким образом, константа равновесия – есть отношение произведений парциальных давлений продуктов реакции к произведению парциальных давлений исходных веществ, взятых в степенях, равных стехиометрическим коэффициентам реакции. зависит только от температуры и от природы взаимодействующих частиц. 45

46 Для гетерогенных реакций, в которых помимо газообразных компонентов участвуют вещества в конденсированных (твердых или жидких) фазах, в выражение константы равновесия парциальные давления паров этих веществ не входят. Это правило действует, если конденсированные фазы не образуют растворов. Рассмотрим реакцию Оксид железа и железо находятся в реакции в твердом состоянии, и для этой реакции константа равновесия запишется как Равновесие достигается при определенном соотношении независимо от относительных и абсолютных количеств FeO , Fe. Для реакции диссоциации карбоната кальция в которой и - твердые фазы, не образующие растворов, Если конденсированные фазы образуют растворы, то в выражение вводят активности или концентрации.

47 УРАВНЕНИЕ ИЗОТЕРМЫ ХИМИЧЕСКОЙ РЕАКЦИИ Известно, что направление химической реакции определяется знаком изменения энергии Гиббса. Если , то реакция идет в прямом направлении ( слева направо), если , то реакция самопроизвольно должна идти в обратном направлении, если , то система находится в состоянии равновесия. Рассмотрим реакцию при постоянных Р и Т, но в условиях, отличных от равновесных. Уравнение изотермы химической реакции позволяет определить величину для такого случая и определить направление химической реакции. где - парциальные давления компонентов в исходной газовой смеси.

МЕРА ХИМИЧЕСКОГО СРОДСТВА Химическое сродство веществ (компонентов) – это их способность вступать в химическое взаимодействие. За меру химического сродства принимают величину изменения энергии Гиббса реакции. Чем отрицательнее , тем сильнее сродство. Чтобы сравнивать сродство веществ, реакции между ними рассматривают в одинаковых стандартных условиях, т.е. при парциальных давлениях каждого компонента гомогенной реакции равных Па. Для реакции в уравнении изотермы химической реакции в этом случае и уравнение запишется как . 48

ЗАВИСИМОСТЬ КОНСТАНТЫ РАВНОВЕСИЯ ОТ ТЕМПЕРАТУРЫ Уравнение, связывающее изменение с температурой при Р=const, носит название ИЗОБАРЫ химической реакции. Уравнение показывает, что знак производной определяется знаком теплового эффекта реакции. Если производная положительна, то функция является возрастающей. Таким образом, Для эндотермических реакций, для которых , возрастает с ростом температуры. уменьшается с ростом температуры. не зависит от температуры. Для экзотермических реакций , В тех случаях, когда тепловой эффект реакции очень мал (близок к нулю) , 49

Если близко к нулю или рассматривается небольшой . интервал, можно принять Тогда, после интегрирования уравнения получим В-константа интегрирования. Отсюда следует, что график зависимости представляет прямую линию. Если известны для нескольких температур, то, построив график в координатах можно определить константу интегрирования и величину теплового эффекта. Эту же зависимость от Т, можно получить используя известные выражения: температурный 50

Записав И поделив обе части уравнения на (-RT), получим или в общем виде где , . 51 51

ПРИНЦИП Ле Шателье (принцип смещения равновесия). Формулировка: Равновесие смещается в направлении, обратном оказанному на систему внешнему воздействию. Применяя принцип Ле Шателье, можно качественно определить влияние температуры и давления на положение равновесия и предсказать, какие условия будут способствовать протеканию процесса в желаемом направлении. Если в процессе образуется большее число газообразных молей веществ, чем вступает в реакцию, то для смещения равновесия вправо необходимо понижать давление в системе. Если процесс идет с уменьшением числа молей газообразных компонентов, то чтобы повысить его эффективность, нужно повысить давление в системе. Для эндотермических процессов ( ) для смещения равновесия вправо, то есть для более полного протекания процесса, необходимо повышение температуры. Для экзотермических процессов ( )протеканию процесса будет способствовать охлаждение системы. 52

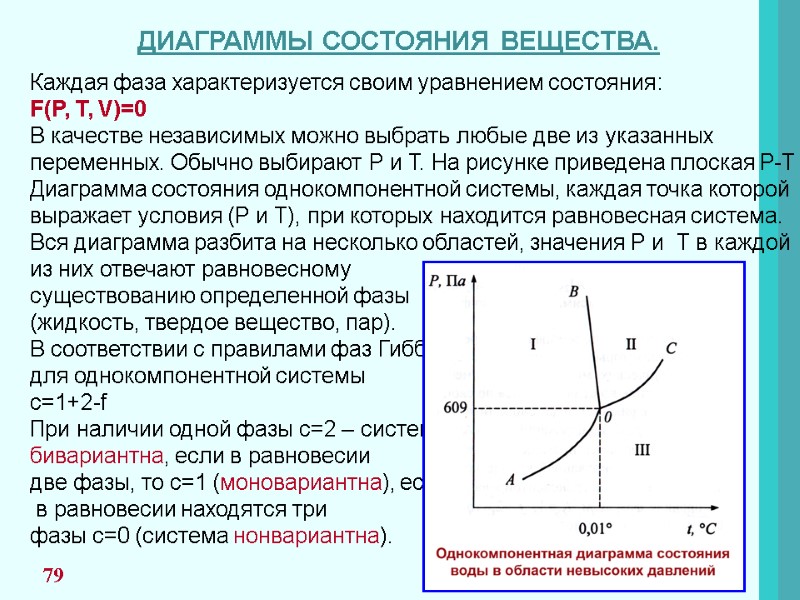
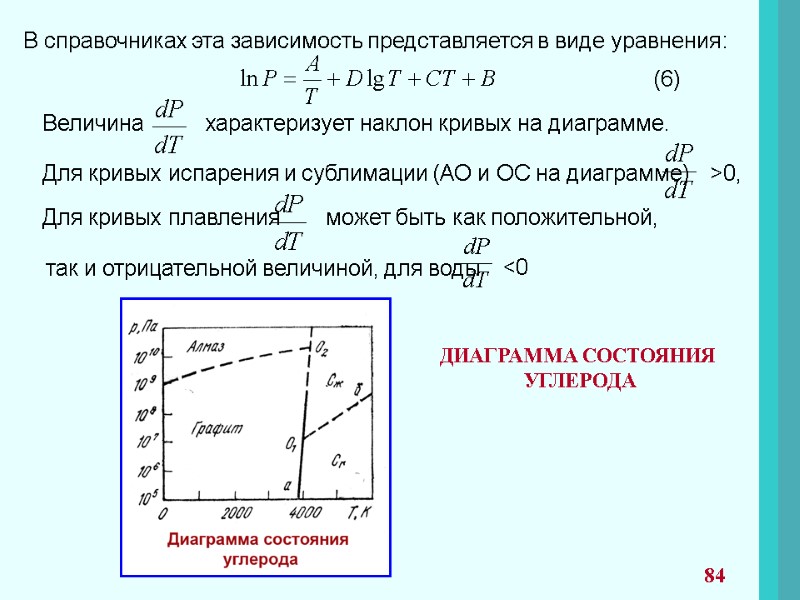
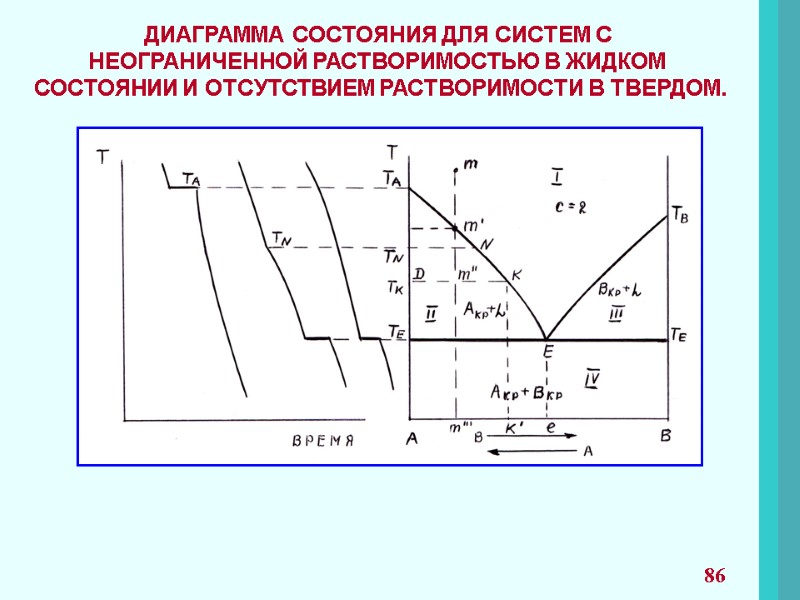
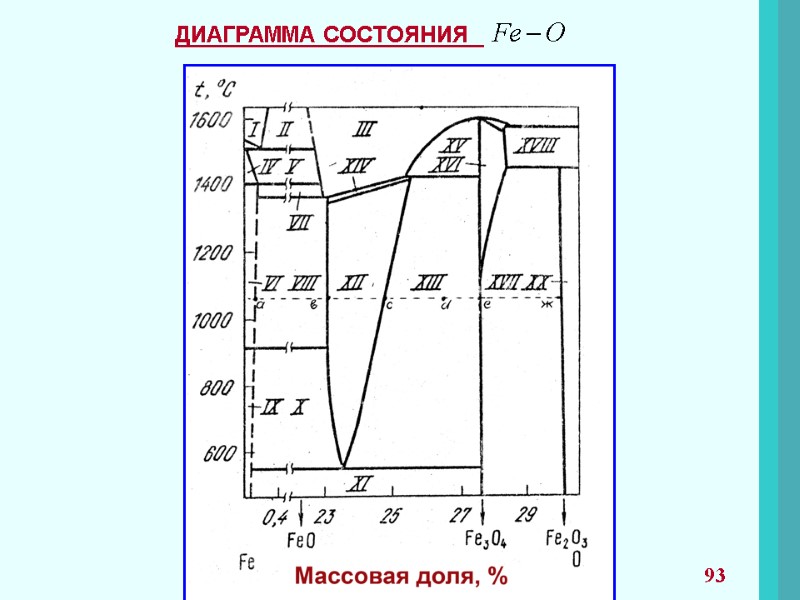
ПРАВИЛО ФАЗ ГИББСА При рассмотрении систем со многими компонентами необходимо знать число фаз, существующих при равновесии, и изменение числа фаз при изменении одного из параметров системы. Правило фаз представляет уравнение: С = К + n – f C – число степеней свободы; К – число компонентов; n – параметры системы; f – число фаз. Число компонентов К – число индивидуальных веществ, входящих в систему, за вычетом числа химических уравнений, связывающих эти вещества. 53

Число степеней свободы С – это число параметров(T, P, концентрации), которые полностью определяют состояние системы при равновесии и которые можно менять в определенных пределах без изменения числа и природы фаз. Часто n=2 (T, P). Если рассматриваются системы с конденсированными фазами, где давление часто не оказывает влияние на состояние системы, правило фаз принимает вид. С = К + 1 – f Число степеней свободы Правило фаз используют при рассмотрении диаграмм состояний и применят для анализа систем, в которых проходят химические превращения. и не может быть меньше нуля. 54

В пределах производства материалов, в частности металлов и сплавов, активно участвуют газовые атмосферы. Источники и процессы ее получения могут быть различны. Так, в металлургии для получения тепла и высоких температур широко используют процессы горения. Под горением понимают прежде всего реакции взаимодействия веществ с кислородом, источником которого часто служит воздух. Используется твердое топливо (кокс), газообразные (газ природный, генераторный, доменный и т.д. ) и жидкое (мазут). В твердом топливе важнейшей горючей составляющей является углерод (С), а в газообразном . и СОСТАВ И СВОЙСТВА ВЫСОКОТЕМПЕРАТУРНЫХ ГАЗОВЫХ АТМОСФЕР Приведем несколько реакций 55

Атмосферы промышленных установок содержат иногда , концентрации могут значительно отличаться. Приведенные реакции и их термодинамические характеристики относят к температурам, не превышающим 2500 К, при которых еще не получают развития явления диссоциации на атомы, радикалы, ионы. В результате реакций формируются состав и свойства газовой фазы. Газовая атмосфера может быть окислительной, восстановительной, нейтральной по отношению к металлам и соединениям, способной науглероживать, азотировать и обезуглероживать металл. Рассмотрим две гомогенные реакции горения (в обратном ) направлении – реакции диссоциации ; Дж/моль(1) ; Дж/моль (2) В соответствие с принципом смещения равновесий реакции полнее протекают с повышением давления и понижением температуры ( ). 56

По правилу фаз при числе компонентов К=2 для однофазной газовой смеси (f=1) и при двух внешних параметрах (P,T) число степеней равно С = К + n – Ф = 2 + 2 – 1 = 3 (3) Это означает, что можно произвольно менять три параметра и это не отразится на числе фаз системы. Для химических реакций это означает, что равновесный состав газовых атмосфер ( ) и ( ) определяются тремя независимыми переменными. Рассмотрим последовательность реакции равновесного состава газовой смеси ( ) – известны Учитывая что получаем , что позволяет рассчитать величину . 57

нужно иметь третье уравнение или задаться величиной одного из парциальных давлений компонентов. Константа равновесия связана со степенью диссоциации Можем составить два уравнения (4) (5) Для нахождения (отношение числа распавшихся молей к их исходному числу). Предположим: в исходном состоянии имеем один моль . После диссоциации в соответствие с реакцией образуется молей , молей и молей . В результате образуется следующее число молей: 58 (6)

Используя связь парциального давления i-го компонента газовой смеси с числом молей получим выражения для парциальных давлений всех трех компонентов. Подставим выражения (8) – (10) в уравнение (4) 59 (7) (8) (9) (10) (11)

Из литературных данных известно: при , , тогда можно записать или Полученное соотношение и является третьим уравнением системы Для характеристики окислительно-восстановительных свойств газовой фазы используется кислородный потенциал Кислородный потенциал газовой фазы - есть разность химических потенциалов кислорода при давлении И стандартном состоянии , то есть при Поскольку 60 и Из уравнения (4) получим выражение для расчета кислородного потенциала газовой смеси при определенных . (13) (12)

61 Если исходный состав газовой смеси отличается от равновесного, то направление протекания реакций определяется с помощью уравнения изотермы реакции.

ОКИСЛИТЕЛЬНО-ВОССТАНОВИТЕЛЬНЫЕ СВОЙСТВА ГАЗОВОЙ ФАЗЫ ПО ОТНОШЕНИЮ К МЕТАЛЛАМ И ИХ ОКСИДАМ В реакциях образования оксидов с учетом одного моля кислорода Если Ме и МеО не образуют растворов тогда , то есть, стандартное изменение энергии Гиббса равно кислородному потенциалу системы Ме - МеО. Кислородные потенциалы газовых фаз можно сравнивать с кислородными потенциалами Ме – МеО. , газовая фаза, металл и оксид металла находятся в равновесии. Если , происходит окисление металла и образование оксида. Если Если , кислород из системы Ме – МеО должен переходить в газовую фазу, то есть должно происходить выделение металла. 62

63 НИЗКОТЕМПЕРАТУРНАЯ ПЛАЗМА. СОСТАВ, СВОЙСТВА, ПРИМЕНЕНИЕ Область существования веществ в твердом и жидком состояниях при нормальном давлении не превышает 4000 - 5000 К. Область существования молекул не намного превышает эту температуру (7000-8000 К). При 10 000 К молекулы отсутствуют, а существуют только атомы, причем, при этих температурах часть ионизируется. Температуры 30 000 – 100 000 К и выше соответствуют полной ионизации. Для газов температуры начала ионизации и полной ионизации составляют: для водорода – 9000 – 30 000 К. для для

64 Различают высокотемпературную (горячую) и низкотемпературную (холодную) плазму. В 1923 г Ленгмюр впервые ввел термин ПЛАЗМА для обозначения полностью ионизированного газа В настоящее время этот термин распространен на частично ионизированные газы, находящиеся при температурах ниже 10 000 К Низкотемпературная плазма – это ионизированный газ, состоящий из большого числа положительно и отрицательно заряженных частиц, а также нейтральных частиц. Важнейшее отличие свойств плазмы от свойств обычной газовой атмосферы состоит в большей роли электромагнитных сил при переносе и взаимодействии ее частиц. Заряженные частицы в отличие от нейтральных, взаимодействуют друг с другом на больших расстояниях, особенно в сфере разряженной плазмы и в условиях вакуума.

65 Плазма характеризуется степенью ионизации и температурой. Степень ионизации определяется отношением количества ионов к исходному количеству частиц n в долях единицы или процентах Степень ионизации в высокотемпературной плазме приближается к 100%, что соответствует плазменному состоянию веществ в недрах солнца. Частицы в плазме обладают энергией 1 ... эВ. Поскольку 1 эВ соответствует энергии теплового движения при температуре 11600 К, область существования такой плазмы находится в интервале температур . Используемая в технике низкотемпературная плазма имеет степень ионизации на уровне 1%, а температура составляет 5000 – 30 000 К. Степень ионизации плазмы зависит от температуры и давления – с повышением температуры и понижением давления степень ионизации увеличивается. Образование низкотемпературной плазмы происходит при неупругих соударениях частиц газа.

66 Различают три типа ионизации: Ионизация ионами Ионизация молекулами (А) Ионизация электронами (е) Понятие «температура газа» имеет конкретный физический смысл в случае термодинамического равновесия системы и характеризует среднюю химическую энергию частиц газа. Полное термодинамическое равновесие в реальной плазме не достигается вследствие неравномерности излучения плазмы, а также в результате постоянного взаимодействия со средой, которое приводит к образованию потоков энергии. Можно говорить только о локальном термическом равновесии то есть о равенстве температур электронов., ионов, нейтральных атомов и молекул в небольшой области вблизи рассматриваемой точки. В реальном плазменном факеле температура меняется по сечению и по длине плазменной струи. Поэтому плазму характеризуют не одним значением температур по объему, а полем температур.

67 Термодинамический расчет состава плазмы включает определение парциальных давлений компонентов при известных величинах температуры и общего давления в небольшой области равновесной плазмы. Рассматриваются реакции диссоциации двухатомных газов на атомы. И реакции ионизации атомов В качестве плазмообразующих газов в технике используются одноатомные Ar , He и двухатомные подвергающиеся электрической ионизации.

68 Устройства, в которых электрическая энергия превращается в тепловую энергию низкотемпературной плазмы, называются плазмотронами. Наиболее распространены дуговые плазмотроны постоянного тока. Между катодом ( вольфрам, графит) и анодом зажигают дугу, а в межэлектродный промежуток подают плазмообразующий газ. Под действием газа дуга выдувается в канал сопла и сжимается. Это вызывает рост температуры и увеличение ионизации. СХЕМЫ ПЛАЗМОТРОНОВ а б а - поток газа параллелен оси дуги б - поток газа направлен по касательной в камеру дуги

69 ПЛАЗМОТРОНЫ высоковольтные (2000-6000 В, 50-500 А) низковольтные (100-800 В, 2000-10 000 А). более длинная дуга, развитая поверхность газа более концентрированное выделение энергии прямого действия косвенного действия анодом является обрабатываемый плазмой материал – жидкая сталь в печи, свариваемый или подвергаемый резке материал анодом является корпус плазмотрона, а нагрев осуществляется выходящим из сопла плазменным факелом. Большинство плазмотронов работает на постоянном токе.

70 Области применения плазмотронов. ХИМИЧЕСКАЯ ПРОМЫШЛЕННОСТЬ высокая температура плазмы позволяет Проводить реакции в газовой фазе с большой скоростью и полнотой. МЕТАЛЛУРГИЯ плавление и переплав металлов, особенно тугоплавких, сварка и резка металлов, плазменное напыление антикоррозийных, жаростойких и износостойких покрытий получение порошков необходимой чистоты и дисперсии, выращивание монокристаллов

71 Плазменная сварка и резка металлов Плазмотроны постоянного тока прямого действия Катодом является графитовый электрод анодом –свариваемый или разрезаемый металл. Применяется для цветных металлов и нержавеющих сталей при больших толщинах металла. Напыления и нанесения покрытий Плазмотроны постоянного тока косвенного действия. Напыляемый материал вводится в состав катода и при его плавлении поступает в виде мелких капель в плазменный факел, направленный на изделие, на которое нужно нанести покрытие. Если материал покрытия не электропроводен, он может быть введен в виде порошка в факел. Плазменное бурение горных пород Плазмотроны косвенного действия. Выходящий из плазмотрона факел плазмы вызывает резкий местный перегрев породы, что приводит к ее растрескиванию и разрушению на куски.

Лекция 4 ФАЗОВЫЕ ПРЕВРАЩЕНИЯ Одно и то же вещество может находиться в разных фазах, причем при определенных условиях разные фазы одного и того же вещества могут находиться в равновесии друг с другом. Процессы перехода вещества из одной фазы в другую, не сопровождающиеся химическими реакциями, называются фазовыми превращениями. Фазовое равновесие означает одновременное сосуществование термодинамически равновесных фаз в гетерогенной системе: Жидкость-пар, Твердое-жидкое, Жидкость-жидкость(несмешивающиеся). К фазовым превращениям относятся: Плавление Кристаллизация Испарение и конденсация Возгонка Изменение кристаллической модификации и магнитного состояния 72

Фазовые превращения, сопровождающиеся выделением или поглощением теплоты, которые называются скрытой теплотой превращения, относят к фазовым переходам первого рода. Переход вещества из одной кристаллической модификации в другую, когда нет выделения или поглощения тепла, относят к фазовым переходам второго рода. Основной характеристикой фазовых переходов является «точка перехода», т.е. температура, при которой разные фазы одного и того же вещества находятся в равновесии. 1539 ºС – температура плавления железа, в равновесии существует твердая и жидкая фаза. 73

ПЛАВЛЕНИЕ И КРИСТАЛЛИЗАЦИЯ При подводе тепла к кристаллическому телу (металлу) возрастает энергия колебательного движения атомов, и при определенной температуре исчезает кристаллическая решетка. Некоторое время подводимое тепло затрачивается на разрыв межатомных связей в кристалле и температура не повышается. Нагрев и плавление кристаллического вещества удобно представить в координатах температура - время. Точка 1 – начало плавления Точка 2 – окончание плавления 74

Аморфные тела представляют собой переохлажденные жидкости и не имеют определенной температуры перехода из твердого состояния в жидкое. Этот переход совершается непрерывно, а не скачком, поскольку жидкости и аморфные тела различаются лишь степенью подвижности молекул. При плавлении обычно объем тела возрастает на 3-6% Затрачиваемое при плавлении тепло называется теплотой плавления. Теплота плавления составляет не более 10% от теплоты сублимации. Некоторые вещества уменьшают свой объем при плавлении: Si, Ge, Bi, Sb. Это же наблюдается при плавлении льда. При охлаждении кристаллизация часто начинается при некотором переохлаждении жидкости, что связано с образованием зародышей кристаллизации и ростом кристаллов. При кристаллизации выделяется такое же количество теплоты, что и при плавлении. Температура плавления зависит от давления. 75

ИСПАРЕНИЕ И КОНДЕНСАЦИЯ Переход жидкости в газообразное (парообразное) состояние называется испарением, переход в газообразное состояние твердого тела – сублимацией. При испарении или сублимации вещество покидают наиболее быстро двигающиеся частицы, вследствие чего средняя энергия остающихся частиц уменьшается и тело охлаждается. Для поддержания постоянной температуры у тела, которое испаряется или сублимирует, к нему нужно непрерывно подводить тепло. Количество теплоты, которое нужно передать единице массы вещества, чтобы превратить его в пар, находящийся при той же температуре, что и само вещество, называется удельной теплотой испарения (или сублимацией). При конденсации вся теплота, которая затрачена на испарение вещества, возвращается обратно и конденсат (жидкость или твердое тело) нагревается. 76

Что означает равновесие жидкость- пар? При испарении всегда имеет место обратный процесс, когда частицы вещества (атомы, молекулы) из паровой фазы переходят в жидкую (или твердую). При каком-то определенном давлении пара количество покидающих жидкость частиц и возвращающихся в нее станут равными. Начиная с этого момента при Т=const плотность пара становится неизменной. Это подвижное равновесие будет оставаться неизменным, если останутся неизменными объем и температура системы. Пар, находящийся в равновесии со своей жидкостью, называется насыщенным. Давление, при котором существует равновесие, называется давлением (упругостью) насыщенного пара. 77

Важнейшей характеристикой является точка кипения вещества - температура, при которой давление насыщенного пара становится равным одной атмосфере. Пар, при определенном давлении, имеющий по сравнению с насыщенным паром более высокую температуру, называется перегретым паром, более низкую – пересыщенным паром. Состояние пересыщенного пара неустойчиво, обычно самопроизвольно наступает конденсация и пар становится насыщенным. Температура, при которой перегретый пар при Р=const становится насыщенным называется точкой росы. При этой температуре начинается конденсация пара, на стенках сосуда и образуется жидкая фаза-роса. Перегретый пар при Р=1 атм. подчиняется закону идеальных газов. Фазовые равновесия лучше всего представить в виде диаграмм состояния. Строятся фазовые диаграммы на основе экспериментальных данных. Диаграммы состояния определяют равновесные состояния в которых вещество при неизменных внешних условиях может пребывать сколь угодно долго. 78

Каждая фаза характеризуется своим уравнением состояния: F(P, T, V)=0 В качестве независимых можно выбрать любые две из указанных переменных. Обычно выбирают Р и Т. На рисунке приведена плоская Р-Т Диаграмма состояния однокомпонентной системы, каждая точка которой выражает условия (Р и Т), при которых находится равновесная система. Вся диаграмма разбита на несколько областей, значения Р и Т в каждой из них отвечают равновесному существованию определенной фазы (жидкость, твердое вещество, пар). В соответствии с правилами фаз Гиббса для однокомпонентной системы с=1+2-f При наличии одной фазы с=2 – система бивариантна, если в равновесии две фазы, то с=1 (моновариантна), если в равновесии находятся три фазы с=0 (система нонвариантна). ДИАГРАММЫ СОСТОЯНИЯ ВЕЩЕСТВА. 79

ДИАГРАММА СОСТОЯНИЯ ВОДЫ Область I, ограниченная линиями АО и ОВ – это твердая фаза-лед. При любых температурах и давлениях, отвечающим этой области, устойчиво существует только лед. Если в эти условия поместить пар или жидкую воду, то они превратятся в лед. Область II, ограниченная ВО и ОС, отвечает условиям существования жидкой воды. Область III, ограниченная линиями АО и ОС, отвечает условиям существования паровой фазы. Поскольку для каждой их областей с=2, это означает, что в пределах каждой области можно произвольно изменять температуру и давление без изменения числа фаз. 80

Кривая ОВ соответствует условиям равновесия: лед-вода, кривая ОС – условиям равновесия: вода - пар, кривая АО – условиям равновесия: лед – пар. Каждая из точек на этих кривых соответствует одновариантной системе с=1+2-2=1, т.е. можно произвольно менять только температуру или только давление. Причем, каждой определенной температуре соответствует только одно определенное давление и наоборот. В точке О, называемой тройной точкой, кривые АО, ВО и СО сходятся. Эта точка отвечает условию трехфазного равновесия, с=0, система нонвариантна. Координаты тройной точки воды: t=0,0098 ºС, Р=609 Па. При изменении температуры или давления одна из фаз исчезает, и мы окажемся на линии (двухфазное равновесие) или в одной из трех областей (однофазное равновесие). 81

УРАВНЕНИЕ КЛАПЕЙРОНА – КЛАУЗИУСА. Закономерности фазовых переходов описывает уравнение Клапейрона-Клаузиуса, представляющее зависимость Р от Т при равновесии двух любых фаз. (1) - теплота фазового перехода Так, при испарении жидкости и конденсации пара (кривая ОС) (2) - удельная теплота испарения. - давление насыщенного, т. е. равновесного с жидкой фазой, пара. - объем моля вещества в парообразном состоянии. - объем моля вещества в конденсированном (жидком) состоянии. Поскольку , то величиной можно пренебречь. 82

Допустив, что пар подчиняется уравнению состояния идеального газа в виде: , уравнение (2) можно записать: или (3) Предположив, что , после интегрирования или (4) Если исследуется большой интервал температур, то следует учитывать зависимость от температуры. Если зависимость приводится в виде , то получим: (5) 83

В справочниках эта зависимость представляется в виде уравнения: (6) Величина характеризует наклон кривых на диаграмме. Для кривых испарения и сублимации (АО и ОС на диаграмме) >0, Для кривых плавления так и отрицательной величиной, для воды <0 может быть как положительной, ДИАГРАММА СОСТОЯНИЯ УГЛЕРОДА 84

ДИАГРАММЫ СОСТОЯНИЯ ДВУХКОМПОНЕНТНЫХ СИСТЕМ. Для создания новых материалов и технологий их производства важнейшей задачей является знание связи между составом и свойствами сложных систем. В металлургии, например, важнейшими свойствами являются температура плавления фаз, температура равновесия между твердыми и жидкими фазами и их зависимость от состава. Диаграммы состояния двухкомпонентных систем позволяют определять число и вид фаз, находящихся в равновесии при определенных условиях, массовые соотношения между фазами для любой температуры. 85

ДИАГРАММА СОСТОЯНИЯ ДЛЯ СИСТЕМ С НЕОГРАНИЧЕННОЙ РАСТВОРИМОСТЬЮ В ЖИДКОМ СОСТОЯНИИ И ОТСУТСТВИЕМ РАСТВОРИМОСТИ В ТВЕРДОМ. 86

Слева представлены на рисунке кривые охлаждения, поясняющие методику построения диаграммы. и соответственно температуры плавления компонент А и В. Это же следует и из правила фаз Гиббса: при что и температура должна быть константой. Температура затвердевания- температура равновесная. Координаты диаграммы: Ордината-температура, Абсцисса-ось составов. Слева чистый компонент А, в этой точке концентрация компонента В 0%. Справа 100% В и соответственно 0% А. Этому типу диаграмм соответствуют системы: Pb – Ag Cd – Bi CaO – MgO NaCl – KCl и др. Наличие остановки на кривой 1 при Т= показывает, что при Р=const Затвердевание происходит в изотермических условиях (Т=const). с=1+1-2=0, это означает, 87

ДИАГРАММА СОСТОЯНИЯ ДЛЯ СИСТЕМ С НЕОГРАНИЧЕННОЙ РАСТВОРИМОСТЬЮ В ЖИДКОМ И ТВЕРДОМ СОСТОЯНИИ. Подобный тип диаграмм имеют системы: Fe – Ni Cu – Ni Ag – Au Ge – Si FeO – MnO 88

ДИАГРАММА СОСТОЯНИЯ ДЛЯ СИСТЕМ С ПРОЧНЫМ ХИМИЧЕСКИМ СОЕДИНЕНИЕМ. 89

ПРАВИЛО РЫЧАГА. С помощью диаграмм состояния можно определять составы и вид равновесных фаз, но и количественное соотношение между ними. Это делается с помощью правила рычага. МАССЫ СОСУЩЕСТВУЮЩИХ ФАЗ ОБРАТНО ПРОПОРЦИОНАЛЬНЫ ОТРЕЗКАМ, НА КОТОРЫЕ ДЕЛИТ КОННОДУ ФИГУРАТИВНАЯ ТОЧКА. КОННОДА СОЕДИНЯЕТ ТОЧКИ, ОТВЕЧАЮЩИЕ СОСТАВАМ ЭТИХ ФАЗ. Для первой диаграммы: Длина отрезка Dm``пропорциональна количеству жидкой фазы, состав которой определяется точкой К, а длина отрезка m``K пропорциональна количеству твердой фазы А. Если известно общее количество двухкомпонентного вещества (сплава) Q, то Из уравнения правила рычага находим, исключив, например , 90

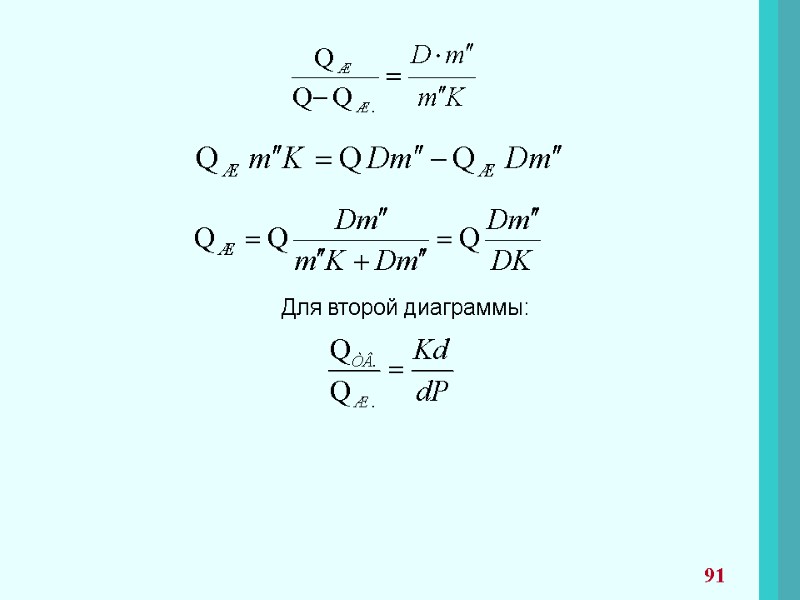Для второй диаграммы: 91

ДИАГРАММА СОСТОЯНИЯ 92

ДИАГРАММА СОСТОЯНИЯ 93

РАСТВОРЫ. КОНЦЕНТРАЦИЯ. ПАРЦИАЛЬНЫЕ МОЛЬНЫЕ ВЕЛИЧИНЫ. Раствором называется однородная, состоящая из 2-х и более веществ система, состав которой может в определенных пределах непрерывно изменяться. Раствор – однофазная система. Химические соединения также однородны, но их состав изменять непрерывно нельзя, так как они подчиняются законам кратных соотношений. Образование растворов сопровождается уменьшением свободной энергии и является самопроизвольным процессом. Частицы компонентов растворов взаимодействуют между собой. В растворах двух сжиженных газов гелия и аргона взаимодействие имеет физический характер, в других часто химический или тот и другой. Из-за взаимодействия компонентов, находящихся в растворе, их поведение отличается от поведения компонентов в «чистом» состоянии. ЛЕКЦИЯ 5 94

95 Для выражения состава раствора на практике часто используют массовые доли ( % по массе ), в теории – мольные (атомные) доли и проценты. В металлургии концентрация компонента i в жидком металле обозначается: lil или i , в оксидном расплаве (i) В числителе число молей компонента в знаменателе – сумма чисел молей всех компонентов раствора. - концентрация компонента i ( % по массе ) - молекулярная ( атомная ) масса компонента i

96 Под молем раствора понимают такое количество раствора, в котором числа молей компонентов равны их мольным долям ( ), а потому сумма чисел молей компонентов равна 1. Раствор имеет свои свойства. Вклад компонентов раствора в эти свойства оценивают с помощью парциальных мольных величин, под которыми понимают частные производные от экстенсивных свойств раствора (зависят от количества вещества: V, H, S, G и т.д.) по числу молей данного компонента ( при Т=const, P=const, ) = т.е. Т.е. представляет собой приращение свойства бесконечно большого количества раствора при добавлении 1 моля i-го компонента. Парциальные мольные величины являются интенсивными характеристиками. Они зависят не от количества раствора , а от его концентрации.

97 Особое место среди парциальных мольных величин занимает химический потенциал компонента = - означает переход компонента i из раствора в паровую фазу. , Величина характеризует стремление компонента покинуть раствор или, наоборот, перейти в него из другой фазы. ПРИМЕР - означает переход компонента i из паровой фазы в раствор. Поскольку в газовой фазе , а при равновесии: то химический потенциал компонента в растворе связан с его парциальным давлением в газовой фазе pi

98 ИДЕАЛЬНЫЕ РАСТВОРЫ. ЗАКОНЫ РАУЛЯ И ГЕНРИ. Основой для описания свойств реальных растворов являются 2 закона: Рауля и Генри. Идеальные растворы – это модели растворов, в которых законы Рауля и Генри выполняются с абсолютной точностью. Оба закона устанавливают зависимость давления пара компонента над раствором от концентрации этого компонента в растворе. Сначала эти законы были установлены опытным путем. Оказалось, что для реальных растворов они выполняются только для ограниченных концентраций компонентов в растворе. Потом были разработаны модели идеальных растворов, в которых законы выполняются с абсолютной точностью для любых концентраций компонентов.

99 Рассмотрим зависимость давления пара одного из компонентов бинарного (двухкомпонентного) раствора от его концентрации на примере системы Fe – Cu Из рисунка видно, что давление пара над раствором всегда меньше давления пара над чистой медью, но повышается при увеличении концентрации меди в расплаве. Проведенные на графике две линии отвечают двум типам идеальных растворов. Согласно этому закону давление пара компонента прямо пропорционально его мольной доле. В идеальном растворе 1-го типа действует закон Рауля. ( линия 1 ). Где - давление пара над чистой медью (Ncu=1) - мольная доля меди в растворе

100 Идеальные растворы первого типа называют совершенными. К совершенным растворам близки реальные растворы, образованные из компонентов, мало отличающихся своими физико-химическими свойствами: Fe – Mn, Fe – Co, FeO – MnO и другие. Возможность описания зависимости Pi от Ni для реальных растворов зависит от требуемой точности: с меньшей точностью можно описать большее количество реальных растворов и посчитать их близкими к совершенным. Для системы Fe – Cu, PCu подчиняется закону Рауля только в небольшой области концентраций вблизи чистой меди. При остальных концентрациях наблюдаются положительные отклонения от закона Рауля – реальное значение PCu больше теоретического. Характер отклонения от закона Рауля ( положительный или отрицательный) связан с химической природой компонентов раствора. Если компоненты проявляют склонность к химическому взаимодействию, например, образовывать соединения, то такой раствор имеет отрицательное отклонение.

101 ПРИМЕР Fe – Si, Fe – Al, Fe – Ti, Fe – V и другие На диаграммах этих систем видно, что с понижением температуры там образуются соединения. Если между компонентами преимущественно действуют силы отталкивания ( Fe – Cu ), то отклонения от закона Рауля будут положительными. При сильных положительных отклонениях наблюдается расслоение на две несмешивающиеся жидкости. ПРИМЕР Fe – Ag, Fe – Pb. Идеальным раствором 2-го типа является разбавленный раствор, в котором согласно закону Генри, давление пара растворенного компонента прямо пропорционально его концентрации ( линия 2 ).

102 Компонент i не является растворителем. константа ( постоянная ) Генри зависит от природы компонентов раствора и от выбранных единиц выражения концентраций. концентрация растворенного компонента Она может быть выражена в любых единицах, в том числе и в % по массе. В общем случае Но для совершенных растворов, если концентрации выражены в мольных долях. Концентрационный интервал, в котором реальные растворы подчиняются закону Генри, колеблется от долей процента до нескольких процентов.

103 ТЕРМОДИНАМИЧЕСКАЯ АКТИВНОСТЬ Для реальных растворов количественной характеристикой, учитывающей как концентрацию компонента, так и его взаимодействие с другими компонентами раствора является активность. Под активностью компонента в растворе понимают отношение парциального давления пара компонента над раствором к давлению пара этого же вещества, находящегося в стандартном состоянии . Очевидно, что в стандартном состоянии активность равна 1. За стандартное состояние можно принять чистый компонент и связь между и выражает соотношение Тогда - коэффициент активности

104 Если соблюдается закон Рауля, то как следует из приведенных уравнений: и , и При отрицательных отклонениях от закона Рауля При положительных отклонениях Коэффициент активности количественно характеризует отличие реального раствора от идеального при определенной концентрации. Для системы Fe – Cu (см. рис.) это отличие проявляется наиболее сильно в разбавленном растворе и постепенно уменьшается с увеличением концентрации ( NCu ). Поэтому в бесконечно разбавленном растворе коэффициент активности по отношению к чистому компоненту ( ) С увеличением концентрации приближается к единице. имеет , как правило, максимальное или минимальное значение ( в зависимости от знака отклонения от идеального

105 Наряду с рассмотренным способом определения активности существует другой способ, в котором рассматриваются отклонения от закона Генри. За стандартное состояние компонента в этом случае принимают идеальный разбавленный раствор с концентрацией . Если выражено в % по массе, то стандартным состоянием является 1 %-ый раствор, подчиняющийся закону Генри. Активность, определенная вторым способом, обозначается . Согласно общему определению активности в стандартном состоянии, Если раствор подчиняется закону Генри, то при других концентрациях компонентов в растворе =1 может быть >1 и <1

106 Для описания отклонений реальных растворов от закона Генри служит коэффициент активности В области идеального разбавленного раствора При положительных отклонениях от закона Генри При отрицательных отклонениях . В конкретном случае стандартные состояния выбирают из соображений удобства. Если нужно учесть отличие свойств растворенных компонентов от свойств чистых веществ, то за стандартное состояние принимают «чистый компонент». Для систем с ограниченной растворимостью в качестве стандартного состояния принимают 1%-ый идеальный разбавленный раствор. Также делают для расплавов с небольшой концентрацией растворимых компонентов. - концентрация i-го компонента металлического расплава, % масс. Итак:

107 РЕАЛЬНЫЕ РАСТВОРЫ. ПАРАМЕТРЫ ВЗАИМОДЕЙСТВИЯ. Для описания поведения компонентов в реальных растворах используют уравнения для идеальных растворов, заменяя концентрации активностями. Если за основу принимают уравнения для совершенного раствора, когда за стандартное состояние принимают чистый компонент, выражение для химического потенциала имеет вид: -химический потенциал компонента в стандартном состоянии ( при ) -активность компоненты в растворе - коэффициент активности -мольная доля компонента

108 Изменение свободной энергии компонента при изотермическом переходе из стандартного состояния (чистое вещество) в раствор с концентрацией составляет: Первое слагаемое уравнения представляет собой избыточную свободную энергию растворения, т.е.

109 Разложение функции в ряд Тейлора вблизи точки, отвечающей ( стандартное состояние- чистый компонент) чистому растворителю приводит к выражению: коэффициент активности компонента i в бесконечно разбавленном растворе. R -остаточный член разложения 1 - растворитель n -общее число растворенных компонентов i, j, k -компоненты -мольная доля растворителя

110 Входящие в уравнение производные называются молярными параметрами взаимодействия первого и второго порядков и обозначаются - молярный параметр взаимодействия компонента i первого порядка. молярные параметры взаимодействия компонента i второго порядка. Отсюда:

111 Для практических расчетов за стандартное состояние удобнее принимать гипотетический однопроцентный идеальный раствор i –того компонента в растворе 1. В этом случае химический потенциал компонента i равен - химический потенциал компонента i в гипотетическом однопроцентном растворе - активность компонента по Генри - концентрация i компонента в растворе ( расплаве) в массовых %- - коэффициент активности

112 Преобразования функции аналогичные тем, что были сделаны с функцией приводят к уравнению: при

113 Свободный член в уравнении отсутствует, т.к. в стандартном состоянии =1 и Производные уравнения называются массовыми параметрами взаимодействия первого и второго порядков и обозначаются соответственно . массовый параметр взаимодействия компонента i с компонентом j первого порядка. массовый параметр взаимодействия компонента i с компонентом j второго порядка. массовый перекрестный параметр взаимодействия компонента i второго порядка. Уравнение для fi

114 Для металлургических растворов, растворителями в которых являются железо (стали), никель, медь, кобальт (сплавы) величины параметров взаимодействия для определенных температур представлены в таблицах ( Падерин С. Н., Серов Г. В. Физика-химия металлов и неметаллических материалов. М.: МИСиС, 2007.-94 с (№586)) Обычно температурная зависимость параметров взаимодействия имеет вид А и В – компоненты, Т – температура, К.

115 ИСПОЛЬЗОВАНИЕ ПАРАМЕТРОВ ВЗАИМОДЕЙСТВИЯ В РАСЧЕТАХ КОЭФФИЦИЕНТОВ АКТИВНОСТЕЙ И АКТИВНОСТЕЙ КОМПОНЕНТОВ МЕТАЛЛИЧЕСКИХ РАСТВОРОВ. Из теории следует, что коэффициент активности i -того компонента в расплаве сложного состава равен: коэффициенты активности, определяющие влияние компонентов j,k,m...n на коэффициент активности компонента i,т.е. . При логарифмировании приведенного выражения получим: массовые параметры взаимодействия первого порядка концентрации компонентов j, k ,m, ... ,n в расплаве в массовых %. или где

ПРИМЕР РАСЧЕТА Допустим, что металлический раствор содержит 80,0 % Fe , 10,0 %Ni 9,5 % Cr, 0,1 %C, 0,39% Mn, 0,007% O, T=1873 K. Отсюда коэффициент активности кислорода равен: Из таблицы при Т=1873 К Тогда: Активность кислорода 116 , , , ,