ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ Кинематика материальной точки Электронный

ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ

Кинематика материальной точки Электронный конспект для студентов всех специальностей Преподаватель: Савицкая А. В.

библиография основные понятия примеры решения задач - кинематика поступательного движения - кинематика вращательного движения применение теоретический материал история лабораторные работы проверь свои знания

1. Кинематика материальной точки Основные характеристики движения материальной точки Материальная точка – тело, размерами которого можно пренебречь по сравнению с расстояниями других тел. Положение материальной точки определяется по отношению к какому-либо другому, произвольно выбранному телу, которое называется телом отсчета. Тело отсчета, система координат, прибор для измерения времени – образуют систему отсчета. В декартовой системе координат положение материальной точки, задается: , где – радиус-вектор, проведенный из начала системы координат в данную точку.

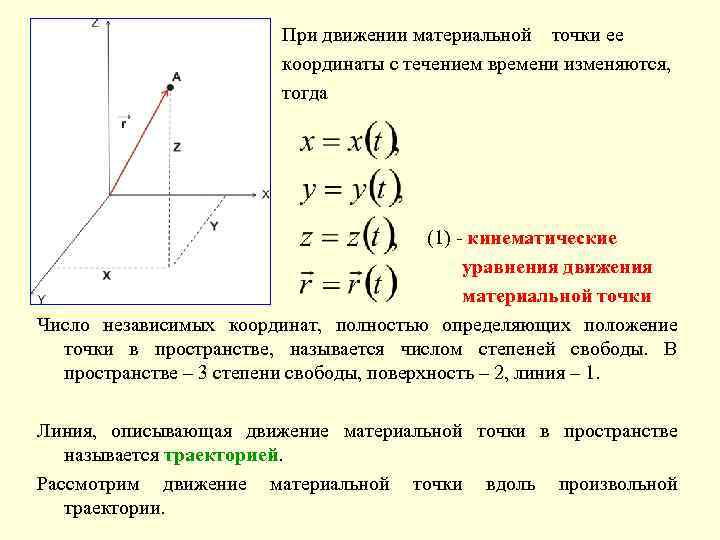При движении материальной точки ее координаты с течением времени изменяются, тогда (1) - кинематические уравнения движения материальной точки Число независимых координат, полностью определяющих положение точки в пространстве, называется числом степеней свободы. В пространстве – 3 степени свободы, поверхность – 2, линия – 1. Линия, описывающая движение материальной точки в пространстве называется траекторией. Рассмотрим движение материальной точки вдоль произвольной траектории.

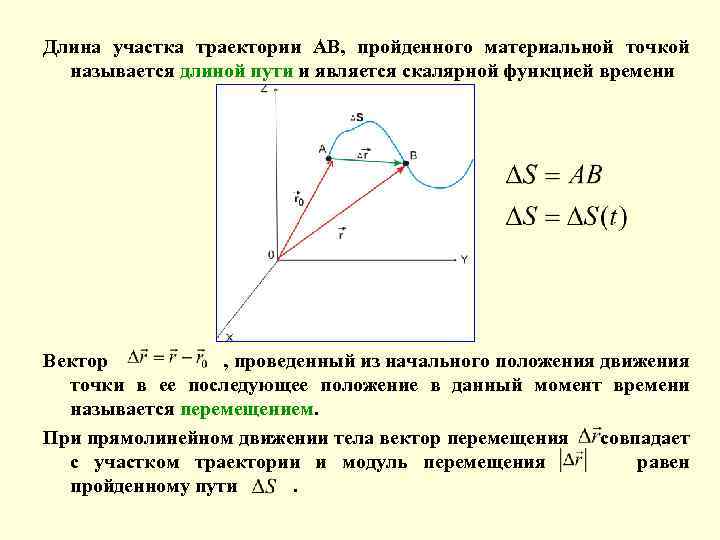Длина участка траектории АВ, пройденного материальной точкой называется длиной пути и является скалярной функцией времени Вектор , проведенный из начального положения движения точки в ее последующее положение в данный момент времени называется перемещением. При прямолинейном движении тела вектор перемещения совпадает с участком траектории и модуль перемещения равен пройденному пути.

Кинематическая характеристика движения – скорость Скорость – векторная физическая величина являющаяся мерой быстроты движения тела и численно равная перемещению, совершаемому телом за единицу времени. Пусть материальная точка движется по какой-либо криволинейной траектории. В течение – малого промежутка времени точка пройдет путь и получит элементарное перемещение. (2) – вектор средней скорости Направление будет совпадать с направлением. При уменьшении средняя скорость стремится к предельному значению, которое называется мгновенной скоростью. (3)

Мгновенная скорость – векторная физическая величина, равная первой производной радиус-вектора по времени. Вектор скорости направлен по касательной к траектории в сторону движения тела. Таким образом, модуль мгновенной скорости равен первой производной пути по времени: (4) При неравномерном движении модуль мгновенной скорости с течением времени изменяется. В этом случае можно определить среднюю скорость неравномерного движения: (5) Из рисунка видно, что. Из формулы (4) следует, что (6). Проинтегрируем левую и правую часть уравнения (6) по времени в пределах от до , найдем длину пути, пройденного материальной точкой (телом) за время :

(7) При равномерном движении числовое значение мгновенной скорости является величиной постоянной, а значит, ее можно вынести за знак интеграла: Длина пути, пройденная материальной точкой за промежуток времени от до определяется выражением:

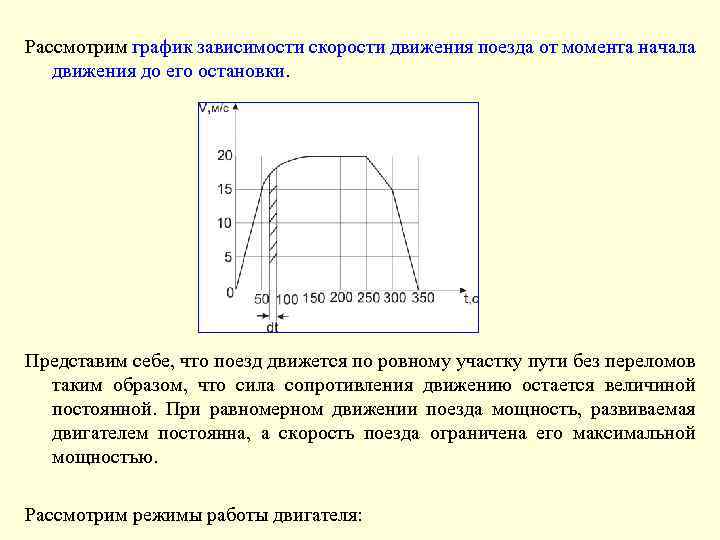Рассмотрим график зависимости скорости движения поезда от момента начала движения до его остановки. Представим себе, что поезд движется по ровному участку пути без переломов таким образом, что сила сопротивления движению остается величиной постоянной. При равномерном движении поезда мощность, развиваемая двигателем постоянна, а скорость поезда ограничена его максимальной мощностью. Рассмотрим режимы работы двигателя:

1. Режим разгона при постоянной силе тяги. Это равноускоренное движение. Скорость нарастает прямо пропорционально времени движения. 2. Режим разгона при постоянной мощности. Он наступает, после достижения поездом критической скорости, при этом потребляемая мощность двигателя достигает номинального значения, а ускорение уменьшается. 3. Режим равномерного движения при постоянной скорости, равной ее максимальному значению. Он наступает, когда при постоянной мощности с ростом скорости движения поезда сила тяги начинает уменьшаться до величины, равной силе сопротивления. 4. Режим выбега. Движение поезда происходит при отключенных тяговых двигателях под действием силы сопротивления движению. Движение является равнозамедленным. Данный режим позволяет уменьшать скорость движения поезда, причем скорость уменьшается по линейному закону. 5. Режим торможения. Производится для остановки поезда. Движение происходит под действием сил торможения и сопротивления. Если силы торможения постоянны, то это равнозамедленное движение с ускорением, которое больше, чем при выбеге.

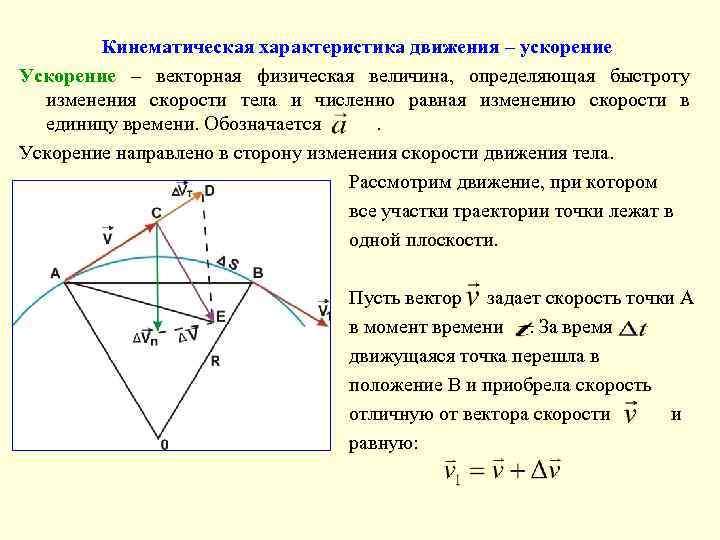Кинематическая характеристика движения – ускорение Ускорение – векторная физическая величина, определяющая быстроту изменения скорости тела и численно равная изменению скорости в единицу времени. Обозначается. Ускорение направлено в сторону изменения скорости движения тела. Рассмотрим движение, при котором все участки траектории точки лежат в одной плоскости. Пусть вектор задает скорость точки А в момент времени. За время движущаяся точка перешла в положение В и приобрела скорость отличную от вектора скорости и равную:

Обозначим - единичный вектор, перпендикулярный касательной и направленный к центру, а через - единичный вектор, параллельный мгновенной скорости. Средним ускорением неравномерного движения в интервале от до называется векторная физическая величина, равная отношению изменения скорости к интервалу времени , (8) Мгновенное ускорение – есть первая производная скорости по времени. (9) Разложим вектор на две составляющие (см. рис. ): Из точки А отложим , - определяет изменение скорости за время по модулю, то есть. вектора характеризует изменение скорости за время по направлению.

(10) - нормальная составляющая ускорения (центростремительное ускорение), направлена по нормали к траектории к центру ее кривизны. - тангенциальная составляющая ускорения, направлена по касательной к траектории движения тела. (11) Полное ускорение тела – геометрическая сумма тангенциальной и нормальной составляющих. (12) Модуль вектора полного ускорения (13)

Частные случаи: 1) , – прямолинейное равномерное движение 2) – прямолинейное равнопеременное движение (14) Если , Из (15) : Проинтегрируем 3) 4) 5) 6) 7) , , , , то обозначив (16). и , получим (15) (17) – прямолинейное движение с переменным ускорением – равномерное движение по окружности - равномерное криволинейное движение – криволинейное равнопеременное движение – криволинейное движение с переменным ускорением.

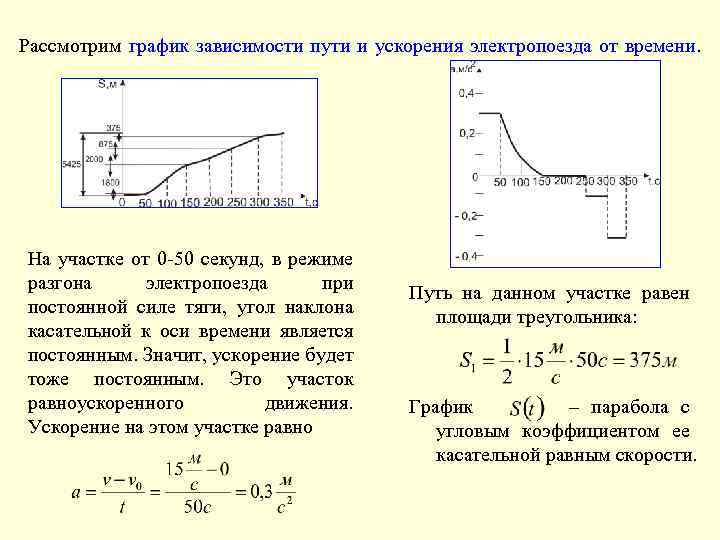Рассмотрим график зависимости пути и ускорения электропоезда от времени. На участке от 0 -50 секунд, в режиме разгона электропоезда при постоянной силе тяги, угол наклона касательной к оси времени является постоянным. Значит, ускорение будет тоже постоянным. Это участок равноускоренного движения. Ускорение на этом участке равно Путь на данном участке равен площади треугольника: График – парабола с угловым коэффициентом ее касательной равным скорости.

На участке от 50 -150 с, в режиме разгона при постоянной мощности, скорость электропоезда возрастает, достигая максимального значения. Угловой коэффициент касательной к оси времени и, соответственно, ускорение постепенно уменьшаются до нуля. Путь можно определить по площади криволинейной трапеции, разбив ее на маленькие квадратики, или рассчитать приближенно как произведение средней скорости на этом участке на время движения электропоезда на данном участке. Тогда, На участке от 150 -250 с, устанавливается режим равномерного движения с максимальной скоростью. Ускорения нет. График – прямая линия, так как угловой коэффициент постоянен. Путь равен площади прямоугольника:

На участке от 250 -300 с, происходит движение электропоезда накатом, в режиме выбега. Скорость уменьшается по линейному закону. Движение является равнозамедленным. Рассчитаем ускорение электропоезда на этом участке: Путь на этом участке равен площади трапеции: На участке от 300 -350 с, в режиме торможения, скорость уменьшается по линейному закону до нуля при остановке. Движение является равнозамедленным. Рассчитаем ускорение электропоезда на данном участке: Путь равен площади треугольника

Общий путь движения электропоезда равен сумме путей на его отдельных участках: Средняя скорость движения электропоезда равна отношению общего пути ко времени движения, то есть

Измерение скорости и ускорения вагона При скатывании вагона с сортировочной горки возникает необходимость определения скорости и ускорения вагона при движении под горкой. Для этого создается измерительный участок длиной L, разделенный на две половины. Далее измеряется время прохождения вагоном каждого из участков и При постоянном уклоне участка ускорение вагона будет постоянно. Зависимость скорости от времени является линейной. Пусть скорость движения вагона на входе в измерительный участок равна. Скорость входа на границу между половинами участка будет равна Запишем уравнение пути при равноускоренном движении вагона на каждой из половин участка:

(18) (19) Уравнения (18) и (19) содержат две неизвестные величины: скорость входа на измерительный участок и ускорение вагона на участке. Выразив из уравнения (18) скорость и подставив в уравнение (19), получим расчетную формулу для ускорения: (20) Затем, подставив полученное выражение для ускорения в формулу скорости входа на измерительный участок, получим (21) Таким образом, по измеренным значениям времени движения на первой и второй половинах участка можно рассчитать скорость и ускорение вагона.

Движение материальной точки по окружности

Движение материальной точки вокруг неподвижной оси Рассмотрим движение твердого тела, которое вращается вокруг неподвижной оси. Отдельные точки этого тела будут описывать окружности, центры которых лежат на оси вращения. Пусть тело движется по окружности радиусом R. Элементарные повороты можно рассматривать как вектор или.

Модуль вектора равен углу поворота, а его направление совпадает с направлением поступательного движения острия винта. Вращение головки винта происходит в направлении движения материальной точки (тела) по окружности. Это правило в физике носит название правила правого винта.

Угловая скорость – векторная физическая величина, равная первой производной угла поворота тела по времени. (1) - псевдовектор (вектор, направление которого связывается с направлением вращения тела; он не имеет определенной точки приложения и может откладываться из любой точки оси вращения). Направление вектора угловой скорости определяется по правилу правого винта. Единица измерения:

Линейная скорость: (2) Если ω=const, то вращение равномерное. Его характеризуют с помощью периода вращения, частоты вращения тела. Обозначим Т – период – время, за которое точка совершает один полный оборот, то есть поворачивается на угол. Тогда, (3) Обозначим n – частота вращения – число полных оборотов в единицу времени. (4)

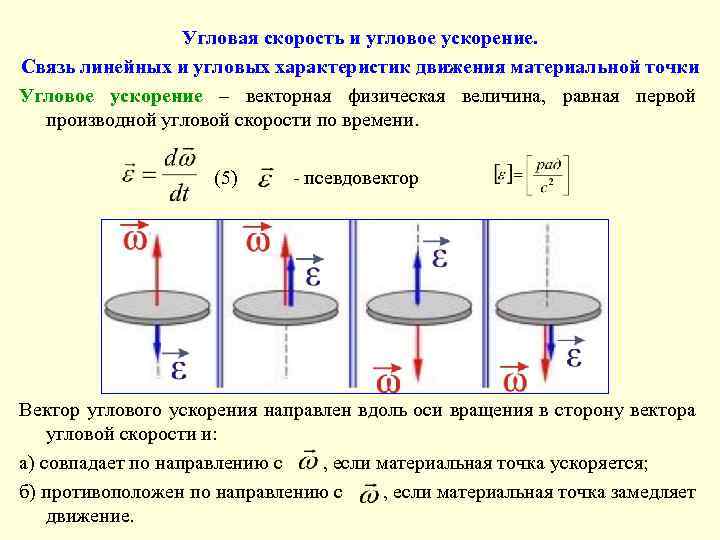Угловая скорость и угловое ускорение. Связь линейных и угловых характеристик движения материальной точки Угловое ускорение – векторная физическая величина, равная первой производной угловой скорости по времени. (5) - псевдовектор Вектор углового ускорения направлен вдоль оси вращения в сторону вектора угловой скорости и: а) совпадает по направлению с , если материальная точка ускоряется; б) противоположен по направлению с , если материальная точка замедляет движение.

Найдем связь линейных и угловых характеристик движения материальной точки (тела): Таким образом, (6) – связь линейного и углового ускорения тела. Вычислим тангенциальную составляющую ускорения: Таким образом, (7). Вычислим нормальную составляющую ускорения: Таким образом, (8).

Таблица соотношения характеристик поступательного и вращательного движений Поступательное движение Вращательное движение Перемещение (угол поворота) Скорость Ускорение Связь Длина пути, пройденного точкой по дуге окружности радиуса R: Угол поворота: Линейная скорость: Угловая скорость: Тангенциальная составляющая ускорения: Нормальная составляющая ускорения: Угловое ускорение:

Поступательное движение Вращательное движение Законы движения Равномерное движение: Равнопеременное движение: , где - начальная линейная скорость. , где - начальная угловая скорость.

Вращательное движение

Динамика материальной точки

Первый закон И. Ньютона. Инерциальные системы отсчета (ИСО) Динамика – раздел механики, изучающий связь между взаимодействием тел и изменением характера движения. Большая заслуга в области механики принадлежит И. Ньютону. Исследования по механике были изложены им в большом труде «Математические начала натуральной философии» , вышедшем в свет в 1687 году. Первый закон Ньютона Всякое тело сохраняет состояние покоя или равномерного прямолинейного движения пока оно не будет выведено из этого состояния воздействием других тел. Свойства тел сохранять состояние покоя или прямолинейного равномерного движения называется свойством инерции. Первый закон Ньютона – закон инерции.

Ньютон как физик признавал принцип относительности движений. Он приводил пример с наблюдением за движением падающего мяча на плывущем судне. Для наблюдателя на судне мяч падает вертикально. Наблюдатель же, находящийся на берегу, видит, что мяч, следуя за движением судна, описывает в воздухе криволинейный путь. Следовательно, описание движения мяча относительно координат, связанных с палубой судна, на котором находится наблюдатель, ничем не будет отличаться от описания движения мяча, подбрасываемого наблюдателем на берегу. Такие системы носят название инерциальных. Ньютон установил, что человек, находящийся в ИСО, не может установить своего движения, если кажется, что движутся окружающие его тела. Но если система находится в ускоренном движении, то это может быть установлено находящимися в ней наблюдателями.

Установим различие между инерциальной и неинерциальной системами отсчета на примере движущегося поезда: Если система координат связана с поездом, то есть перемещается вместе с ним по отношению к поверхности Земли, то для человека, находящегося в поезде, закон Ньютона оказывается применимым только до тех пор, пока поезд находится в покое или прямолинейном равномерном движении. При изменении скорости (например, при резком торможении), некоторые предметы станут опрокидываться, слетать с полок, хотя на них не действуют никакие другие силы. То же происходит при быстром возрастании скорости и при переходе поезда на криволинейный участок пути. Для наблюдателя, находящегося на Земле и пользующегося системой отсчета, связанной с Землей, все явления в поезде будут происходить в полном соответствии с законом инерции. Следовательно, система координат, связанная с Землей, будет инерциальной.

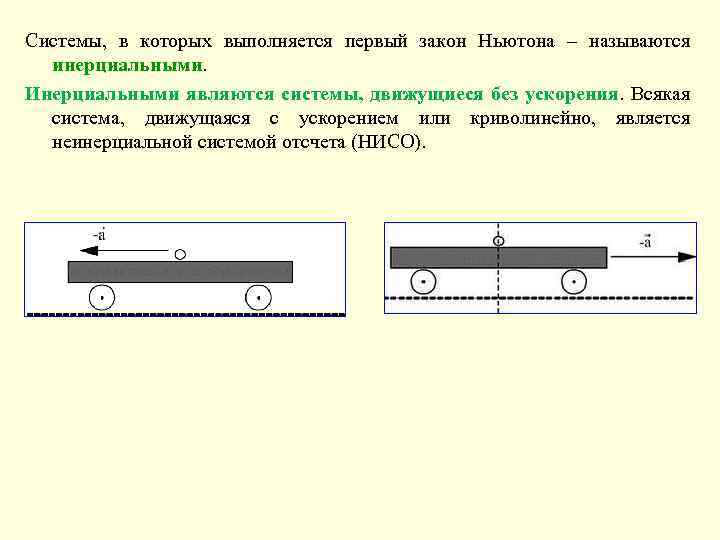Системы, в которых выполняется первый закон Ньютона – называются инерциальными. Инерциальными являются системы, движущиеся без ускорения. Всякая система, движущаяся с ускорением или криволинейно, является неинерциальной системой отсчета (НИСО).

Понятие о силе и ее измерении. Силы в природе. Фундаментальные взаимодействия Заслуга Ньютона состоит в том, что именно он впервые ввел понятие «сила» . Сила – обобщенная мера реальных взаимодействий. Сила – векторная физическая величина, являющаяся мерой взаимодействия тел и численно равная произведению массы тела на сообщаемое этой силой ускорение. Обозначается: F (1) В результате действия силы, тело приобретает ускорение или изменяет свою форму и размеры. Сила характеризуется точкой приложения и направлением. Единица измерения: Физический смысл: 1 Ньютон – сила, с которой телу массой 1 кг сообщается ускорение в 1 м/с2.

Сила упругости – возникает при упругой деформации. (2) - закон Гука (3), где – k - коэффициент упругости пружины – смещение. Закон Гука справедлив в диапазоне небольших деформаций, когда внутренние напряжения в материале тел меньше предела упругости материала. При превышении предела упругости происходит необратимое удлинение тела, пластическое течение материала тела. Пружины, рессоры используются в вагонах и локомотивах как упругие элементы подвески для смягчения ударов колес о стыки рельсов, в автосцепках для смягчения ударов при сцеплении вагонов.

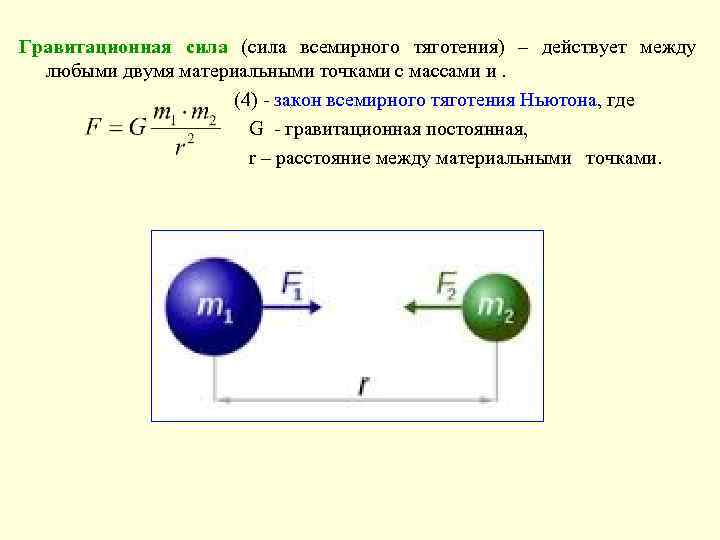Гравитационная сила (сила всемирного тяготения) – действует между любыми двумя материальными точками с массами и. (4) - закон всемирного тяготения Ньютона, где G - гравитационная постоянная, r – расстояние между материальными точками.

Сила тяжести – сила, с которой Земля вследствие земного притяжения притягивает к себе все тела. Точка приложения силы тяжести всегда находится в центре тела. Направлена сила тяжести вертикально вниз к центру Земли. Вычисляется: (5), где g - ускорение свободного падания. Вес тела – это сила, с которой тело давит на опору или растягивает подвес. Точка приложения веса тела находится на опоре или подвесе. Вес тела направлен также как и сила тяжести, вертикально вниз. (6)

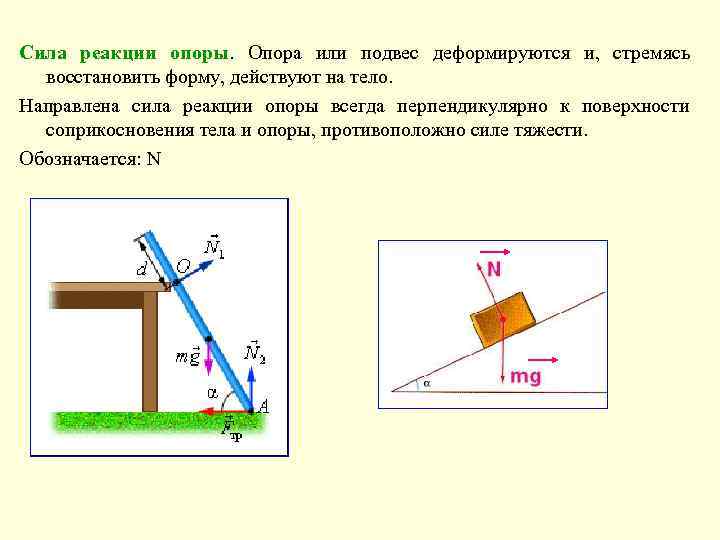Сила реакции опоры. Опора или подвес деформируются и, стремясь восстановить форму, действуют на тело. Направлена сила реакции опоры всегда перпендикулярно к поверхности соприкосновения тела и опоры, противоположно силе тяжести. Обозначается: N

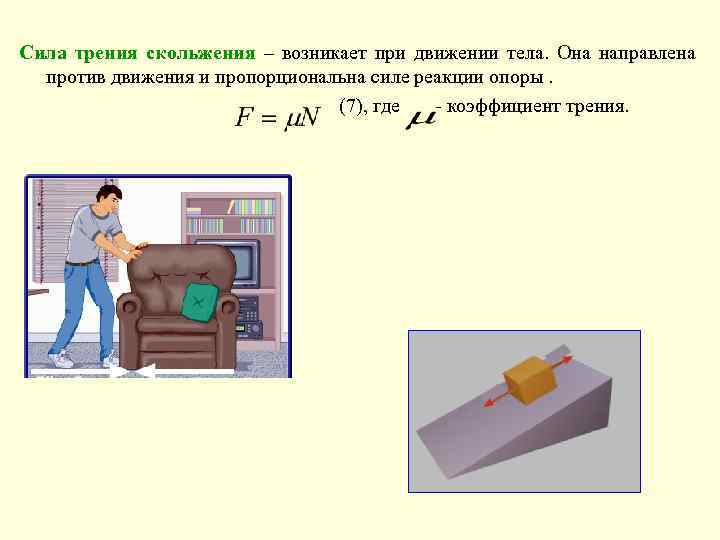Сила трения скольжения – возникает при движении тела. Она направлена против движения и пропорциональна силе реакции опоры. (7), где - коэффициент трения.

Фундаментальные взаимодействия Вид взаимодействия Поле- переносчик взаимодействия Интенсивность взаимодействия Расстояние, на котором взаимодействие является определяющим Объекты, существующие благодаря взаимодействию ядра атомов сильное поле ядерных сил кулоновская сила, электромагнитное обеспечивающая существование атома 1 10 -2 - 10 -4 10 -13 м ∞ молекулы, атомы, элементарные частицы кварки, лептоны слабое гравитационное β- распад гравитационное 10 -40 ∞ космические объекты, галактики, их системы

Современная наука установила только три вида существующих в природе сил. Это гравитационная сила, электромагнитная и ядерная. Таким образом, сил в природе – три, взаимодействия – три, и как будет показано далее законов Ньютона тоже три.

Второй закон И. Ньютона. Масса тела. Принцип независимости сил. Второй закон Ньютона – основной закон динамики поступательного движения. В результате взаимодействия тел, они либо деформируются, либо приобретают ускорение. (8) – второй закон Ньютона Ускорение тела прямо пропорционально действующей силе и обратно пропорционально массе этого тела. (9) – динамическое уравнение движения (10) Учитывая, что масса тела есть величина постоянная, то в выражении (10) ее можно внести под знак производной: (11)

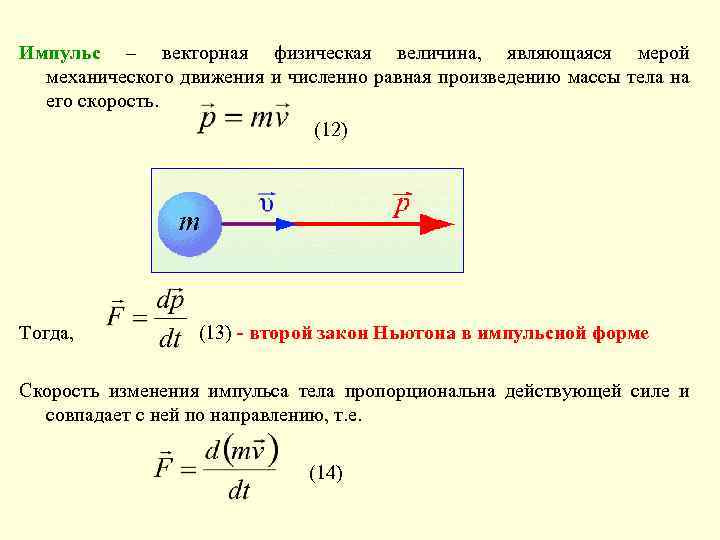Импульс – векторная физическая величина, являющаяся мерой механического движения и численно равная произведению массы тела на его скорость. (12) Тогда, (13) - второй закон Ньютона в импульсной форме Скорость изменения импульса тела пропорциональна действующей силе и совпадает с ней по направлению, т. е. (14)

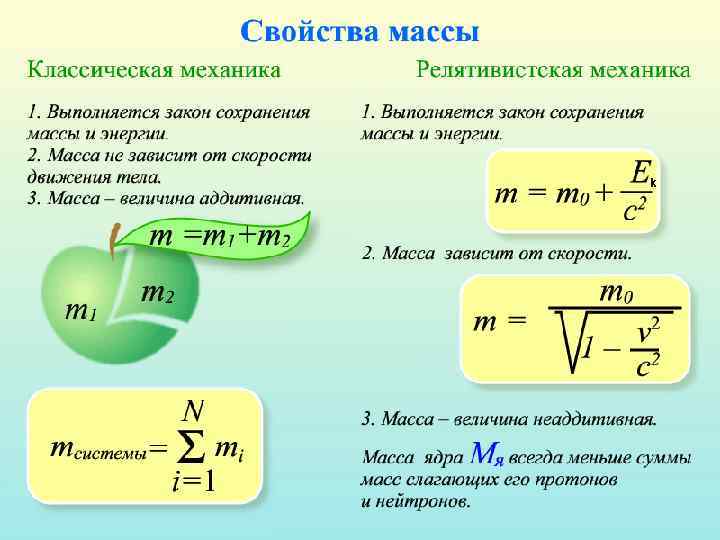
Масса – это скалярная физическая величина, являющаяся мерой инертности тел и численно равная отношению силы, действующей на тело к сообщаемой этой силой ускорению. (15) Единица измерения: . Одним из важнейших положений теории относительности является выяснение связи массы тела со скоростью его движения. Классическая механика (механика Ньютона) исходила из предположения о том, что. Теория относительности исходила из предположения о том, что масса тела, движущегося относительно наблюдателя со скоростью может быть найдена по формуле: - масса неподвижного относительно наблюдателя тела, - скорость света в вакууме. (16) – формула Эйнштейна

– доказал М. В. Ломоносов (1760 г. диссертация «Рассуждение о твердости и о жидкости тел» ). Масса тела обладает свойством аддитивности: масса тела представляет собой сумму масс составляющих тело частей. В механике большое значение имеет принцип независимости сил: если на тело действует несколько сил, то каждая из них сообщает телу ускорение согласно (8) такое, как если бы других сил не было. (17) – принцип независимости сил Принцип независимости сил позволяет разложить силы и ускорения на составляющие, что значительно упрощает решение задач. Если на материальную точку действует сразу несколько сил, то, согласно принципу независимости сил, под силой во втором законе Ньютона понимают результирующую силу.

Третий закон И. Ньютона Силы, с которыми тела действуют друг на друга, всегда равны по модулю и противоположны по направлению. (18) – третий закон Ньютона – сила, действующая на первое тело со стороны второго тела - сила, действующая на второе тело со стороны первого. Особенности выполнения третьего закона Ньютона: 1) Силы приложены к разным телам 2) Силы всегда действуют парами 3) Силы одной природы.

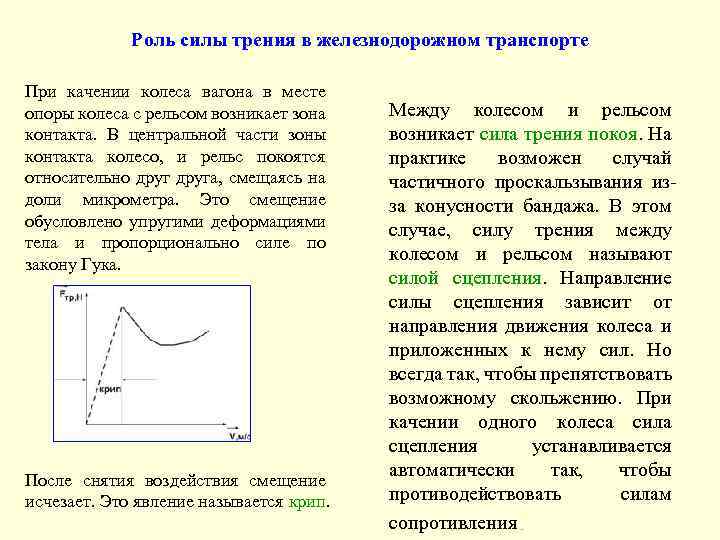Роль силы трения в железнодорожном транспорте При качении колеса вагона в месте опоры колеса с рельсом возникает зона контакта. В центральной части зоны контакта колесо, и рельс покоятся относительно друга, смещаясь на доли микрометра. Это смещение обусловлено упругими деформациями тела и пропорционально силе по закону Гука. После снятия воздействия смещение исчезает. Это явление называется крип. Между колесом и рельсом возникает сила трения покоя. На практике возможен случай частичного проскальзывания изза конусности бандажа. В этом случае, силу трения между колесом и рельсом называют силой сцепления. Направление силы сцепления зависит от направления движения колеса и приложенных к нему сил. Но всегда так, чтобы препятствовать возможному скольжению. При качении одного колеса сила сцепления устанавливается автоматически так, чтобы противодействовать силам сопротивления.

Рассмотрим качение колеса по рельсу. Как было сказано выше, при качении колеса по рельсу происходит деформация, как колеса, так и рельса. Из-за остаточных деформаций уровень рельса за колесом оказывается ниже, чем перед колесом, поэтому колесо при движении должно все время закатываться на подъем. Распределение давления на колесо со стороны рельса оказывается несимметричным: спереди давление больше, а сзади меньше. Точка приложения реакции действия рельса на колесо смещена вперед на небольшое расстояние - b. Сила трения качения пропорциональна силе давления рельса на колесо и определяется: (19) , где - коэффициент трения качения (он зависит от упругости и твердости материала рельса и колеса, и уменьшается с увеличением размеров колеса).

Рассмотрим силу торможения поезда – это сила трения всех тормозящих колес с рельсами. По своей природе это либо сила трения покоя, являющаяся силой сцепления в случае не проскальзывания колеса по рельсу, либо сила трения скольжения при проскальзывании колеса. Силы трения скольжения между бандажом колеса и тормозными колодками создают момент сил трения, который противодействует вращению колеса при его качении по рельсу. При стремлении колеса перестать вращаться, колесо толкает рельс вперед от себя с силой трения рельс. Эта сила приводит к смещению или угону рельсов. А рельс толкает колесо назад с такой же по величине силой трения, которая является силой торможения колеса.

Движение поезда в режиме постоянной силы тяги При движении поезда между станциями поезд можно рассматривать как материальную точку. Движение поезда является поступательным, а значит можно применить основной закон динамики - второй закон Ньютона. Рассмотрим силы, действующие на поезд. На поезд со стороны Земли действует сила тяжести поезда (включая и силу тяжести локомотива). Со стороны рельсов на поезд действуют сила тяги локомотива, направленная по касательной к рельсам, в сторону движения, силы нормального давления (силы реакции опоры) на колеса состава и локомотива, а также в направлении против движения – сила сопротивления качению всех колес поезда. Силы взаимодействия в сцепках между локомотивом и составом, между вагонами являются внутренними силами. Они действуют парами и компенсируют друга таким образом, что существенного влияния на движение поезда не оказывают.

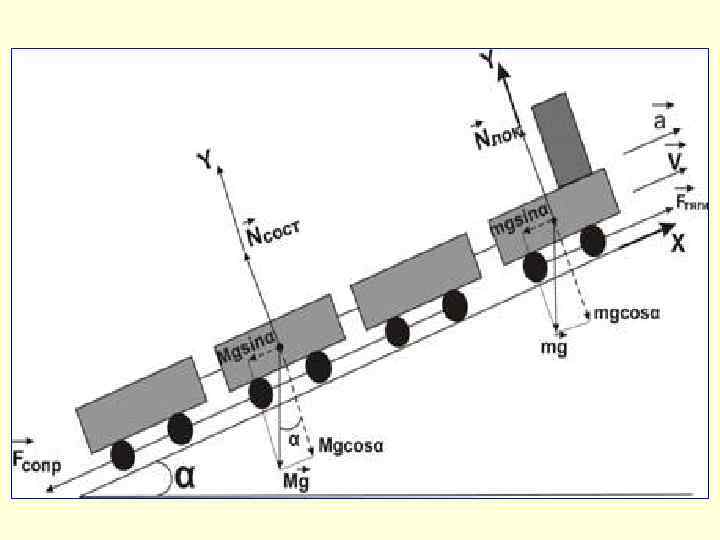
Произведение массы поезда на ускорение поступательного движения равно векторной сумме всех сил, действующих на локомотив и состав. Найдем силу сопротивления всех колес поезда вместе с локомотивом: Уклон железнодорожных путей измеряется как отношение подъема на длину пути. Он не превышает 10 м на 1 км. При движении вверх на подъем, уклон положителен, при спуске – отрицателен. Получим расчетное уравнение для ускорения поезда под действием постоянной силы тяги:

Сила тяги локомотива может изменяться в широких пределах: от нуля до предельной силы сцепления. Обычно, в начале движения поезда, чтобы быстрее набрать скорость, сила тяги локомотива устанавливается равной предельному значению. В этом режиме движение происходит с постепенным увеличением мощности тяговых двигателей. Найдем предельную силу тяги как произведение коэффициента сцепления на силу реакции опоры колес локомотива на рельсы: При , предельная сила тяги будет пропорциональна силе тяжести локомотива, то есть Максимальное ускорение поезда будет равно

Для повышения эффективности перевозок массу состава желательно увеличивать. Поэтому на практике определяют предельную массу поезда для движения на данном перегоне. Рассматривают самый тяжелый участок перегона с наиболее крутым подъемом, а также начало движения, когда коэффициент сопротивления после стоянки больше, чем в движении. Расчетную массу поезда можно определить по формуле: Для увеличения массы состава, необходимо либо увеличивать массу локомотива, применяя несколько локомотивов, либо увеличивать коэффициент сцепления ведущих колес с рельсами. Для этого подсыпают песок под колеса, но это имеет отрицательный аспект, так как приводит к износу колес и рельс. Для облегчения начала движения, состав стараются располагать под уклон. Во время стоянки состава из-за выдавливания смазки коэффициент трения в подшипниках скольжения возрастает в разы, для уменьшения трения подшипники скольжения заменяют роликовыми. Или: локомотивом состав толкается назад, так, чтобы автосцепки вагонов сжались, затем при движении локомотива вперед поочередно сдвигают вагоны.

Динамика системы материальной точки

Основные понятия Системой материальных точек называют любую систему, состоящую из n объектов. Силы взаимодействия тел системы между собой называются внутренними. Силы взаимодействия тел системы с телами не входящими в систему называются внешними. Центром масс системы материальных точек является воображаемая точка, положение которой характеризует распределение массы этой системы. (1) (2)

(3) - формулы для вычисления координат центра масс

Замкнутая система. Закон сохранения импульса в замкнутой системе тел. Систему называют замкнутой, если сумма всех внешних сил равна нулю (если влиянием внешних сил можно пренебречь). Рассмотрим механическую систему, состоящую из n – материальных тел. Запишем второй закон Ньютона для каждого из n тел механической системы, обозначим внутреннюю силу, действующую на i – ое тело со стороны k-го – через : Производная импульса механической системы по времени равна геометрической сумме внешних сил, (4) действующих на систему (5)

Сумма всех внутренних сил будет равна нулю, тогда по третьему закону Ньютона имеем: Тогда (6 ) – полный импульс системы материальных точек. Таким образом, или (7) – закон сохранения импульса. Полный импульс замкнутой системы материальных точек есть величина постоянная.

Движение центра масс. Постоянство скорости центра масс замкнутой системы Перепишем уравнения (3) следующим образом: Продифференцируем по времени: (8) (9) Обозначим: Используя формулы: получим

(10) Тогда, (11) Полный импульс системы материальных точек равен произведению масс всей системы на скорость центра масс.

Продифференцируем по времени: (12) – второй закон Ньютона для системы материальных точек Система материальных точек движется так, как двигалась бы одна материальная точка с массой равной массе всей системы, со скоростью равной скорости центра масс. Практическое применение уравнения (12): мы не можем дать ответа на вопрос как будет двигаться каждая материальная точка, но можем ответить на вопрос, как будет двигаться центр масс системы материальных точек. Если система является замкнутой, то , . Получим: (13) – теорема о движении центра масс Центр масс замкнутой системы материальных точек движется равномерно и прямолинейно. Или: за счет одних внутренних сил положение центра масс системы материальных точек изменить невозможно.

Энергия, работа и мощность в механике Основные понятия Термин «энергия» был введен в 50–х годах XIX в. шотландским инженером и физиком, одним из создателей механической термодинамики, членом Лондонского Королевского общества Ранкином Уильямом Джоном Макуори. Термин «энергия» он применял в сочетании с термином «потенциальная» : «потенциальная энергия» . Энергия – это количественная мера движения материи во всех формах этого движения. В зависимости от того, какие формы движения, присущие данной материальной системе, могут в данных условиях превращаться в механическое движение тел, говорят о разных формах энергии.

Формы энергии: 1. Механическая (механическое движение). 2. Внутренняя (молекулярно-тепловое движение). 3. Электромагнитная. 4. Ядерная. 5. Атомная.

Впервые термин «работа» был введен в науку в 1826 году французским ученым Понселе, хотя содержание понятия использовалось намного раньше. Единица измерения: Работа – это мера изменения энергии тела под действием силы. Рассмотрим элементарное перемещение материальной точки, на которую действует постоянная сила (см. рис). Элементарная работа данной силы будет определяться: (1) – элементарная работа Работа – это скалярная физическая величина, являющаяся мерой изменения энергии тела под действием силы и численно равная произведению вектора силы на перемещение. На участке 1 -2 работу можно вычислить: (2)

Работа силы на участке траектории 1 -2 равна алгебраической сумме элементарных работ на отдельных бесконечно малых участках пути. Зависимость силы от перемещения представлена графически. На графике искомая работа определяется площадью заштрихованной фигуры. (3) (4)

Частные случаи: 1. Если 2. Если 3. Если на тело действует несколько сил (например, две), то работа результирующей силы (как было сказано выше), равна алгебраической сумме работ, совершаемых каждой силой в отдельности, то есть Т. о. (5) Единица измерения работы: – джоуль. 1 Дж – это работа, совершаемая силой 1 Н на пути 1 м.

Мощность – это скалярная физическая величина, являющаяся мерой скорости совершения работы и численно равная: (6) Если за время телом была совершена работа , то средняя мощность за это время выразится формулой: (7) Мощность в данный момент времени будет определяться по (8): В том случае, когда при работе двигателя с постоянной мощностью имеет место равномерное движение со скоростью, формула (8) может быть легко преобразована. Используя формулу для определения пройденного пути из кинематики, получим: (9) Единица измерения мощности: – ватт. 1 Вт – мощность, при которой за время 1 с совершается работа 1 Дж. В технике мощность иногда выражается в лошадиных силах: 1 л. с. =736 Вт.

Кинетическая энергия тела. Связь кинетической энергии тела и работы Как известно, из курса средней школы энергия является величиной относительной. Где - масса покоя частицы , с – скорость света в вакууме, - энергия частицы, - масса частицы в системе отсчета, относительно которой она движется со скоростью V. Обозначим - энергия покоя, тогда (10) - кинетическая энергия тела Выведем известную в физике формулу для нахождения кинетической энергии тела.

, при , получим (11) – кинетическая энергия тела

Кинетическая энергия – это энергия механического движения тела. Она зависит от массы и скорости движущегося тела. Кинетическая энергия системы есть функция состояния ее движения. 1. Кинетическая энергия величина относительная. 2. Кинетическая энергия величина аддитивная. 3. Если скорость тела растет, то кинетическая энергия – увеличивается за счет работы силы, вызывающей увеличение скорости; если скорость тела падает, то энергия тела передается тормозящей системе, при этом кинетическая энергия полностью или частично переходит в другие виды энергий, чаще всего во внутреннюю.

Рассмотрим связь между кинетической энергий и работой совершаемой телом. Используя второй закон Ньютона, а также формулу для определения скорости тела из кинематики, получим: , умножим обе части уравнения на . Проинтегрируем левую и правую части уравнения: , где Таким образом, (12)

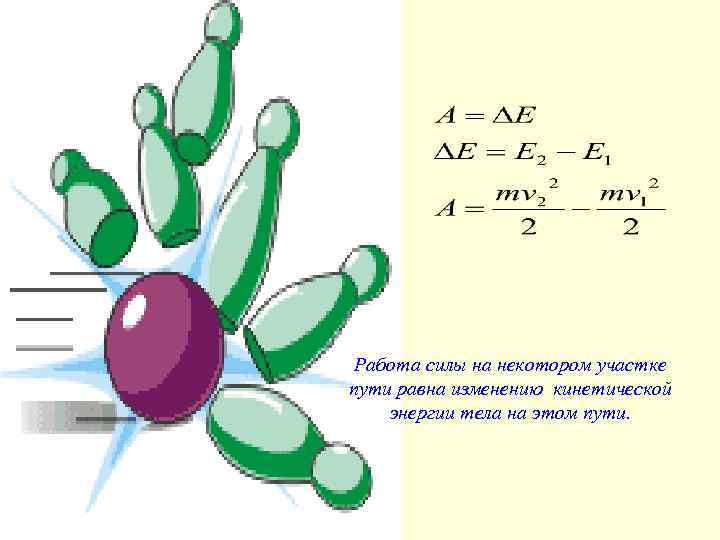Работа силы на некотором участке пути равна изменению кинетической энергии тела на этом пути.

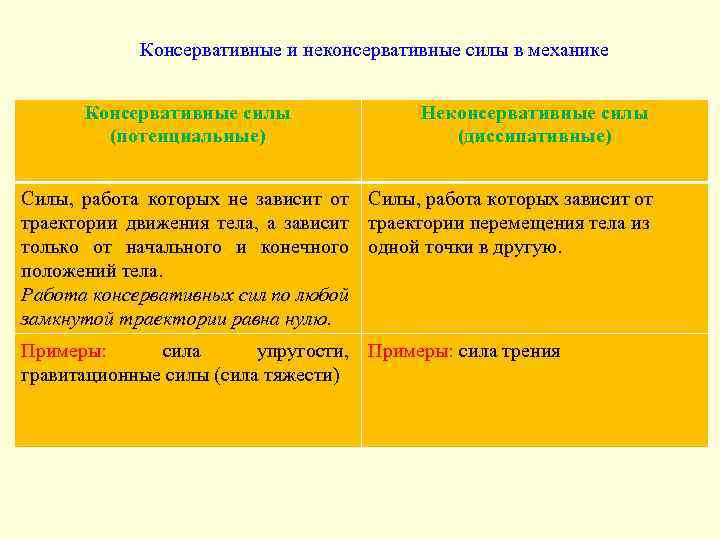Консервативные и неконсервативные силы в механике Консервативные силы (потенциальные) Неконсервативные силы (диссипативные) Силы, работа которых не зависит от Силы, работа которых зависит от траектории движения тела, а зависит траектории перемещения тела из только от начального и конечного одной точки в другую. положений тела. Работа консервативных сил по любой замкнутой траектории равна нулю. Примеры: сила упругости, Примеры: сила трения гравитационные силы (сила тяжести)

Потенциальная энергия и её связь с приложенной к телу силой

Закон сохранения энергии в замкнутой консервативной и неконсервативной системе

Удар шаров: упругий и неупругий Удар – процесс кратковременного столкновения двух и более тел. Силы взаимодействия между сталкивающимися телами – велики, поэтому внешними силами, действующими на нах можно пренебречь. Значит, систему тел можно рассматривать как замкнутую и применить к ней законы сохранения. Тела во время удара деформируются. Кинетическая энергия соударяющихся тел преобразуется в энергию упругой деформации. Центральный удар – при котором тела, до удара движутся вдоль одной прямой, проходящей через центры масс.

Абсолютно упругий удар Абсолютно неупругий удар Столкновение двух тел, в результате которого у взаимодействующих тел не остается никаких деформаций, кинетическая энергия – сохраняется. Столкновения двух тел, в результате которого тела деформируются пластически, движутся совместно, как единое целое. Часть кинетической энергии превращается в работу пластической деформации, кинетическая энергия не сохраняется. Закон сохранения импульса: Закон сохранения кинетической энергии: Если , то Закон сохранения кинетической энергии: Решая данные уравнения, получим: или Если , то и

Применение закона сохранения импульса при сцеплении вагонов Локомотив и вагоны сцепляются для совместного движения в поезд. Сцепление вагонов происходит с помощью автосцепок. Автосцепка предназначена для автоматического сцепления вагонов в состав, передачи тяговых продольных усилий при движении, смягчения сил удара между вагонами при сцепке и движении. Рассмотрим механизм работы устройства автосцепки. Автосцепка состоит из корпуса, в котором находится замок и поглощающий аппарат. Поглощающий аппарат имеет пружину и гаситель колебаний. При сцеплении пружина начинает сжиматься, обеспечивая смягчение силы удара. В гасителе механическая энергия колебаний вагонов превращается в работу сил трения клина при скольжении по корпусу, когда на клин давит конус (см. рис. ). При обратном ходе под действием пружин трение почти отсутствует, и автосцепка возвращается в исходное положение.

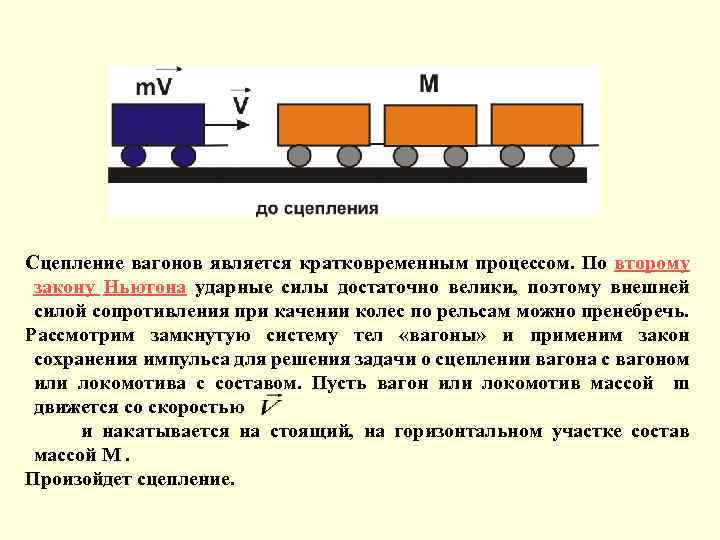Сцепление вагонов является кратковременным процессом. По второму закону Ньютона ударные силы достаточно велики, поэтому внешней силой сопротивления при качении колес по рельсам можно пренебречь. Рассмотрим замкнутую систему тел «вагоны» и применим закон сохранения импульса для решения задачи о сцеплении вагона с вагоном или локомотива с составом. Пусть вагон или локомотив массой m движется со скоростью и накатывается на стоящий, на горизонтальном участке состав массой М. Произойдет сцепление.

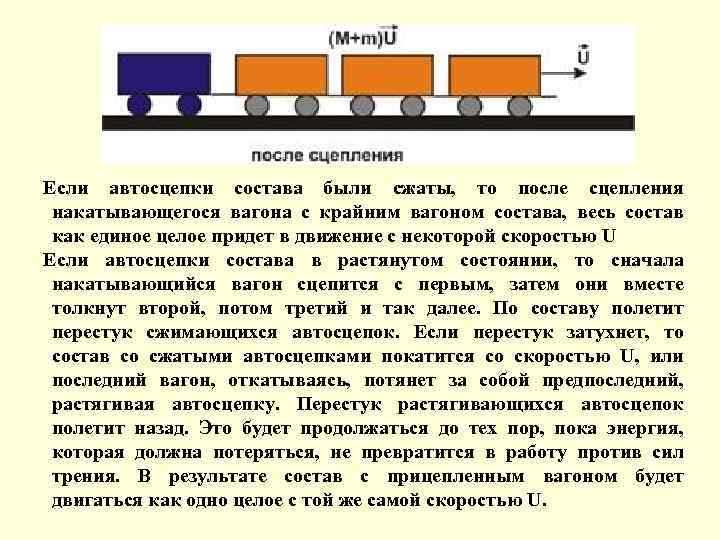Если автосцепки состава были сжаты, то после сцепления накатывающегося вагона с крайним вагоном состава, весь состав как единое целое придет в движение с некоторой скоростью U Если автосцепки состава в растянутом состоянии, то сначала накатывающийся вагон сцепится с первым, затем они вместе толкнут второй, потом третий и так далее. По составу полетит перестук сжимающихся автосцепок. Если перестук затухнет, то состав со сжатыми автосцепками покатится со скоростью U, или последний вагон, откатываясь, потянет за собой предпоследний, растягивая автосцепку. Перестук растягивающихся автосцепок полетит назад. Это будет продолжаться до тех пор, пока энергия, которая должна потеряться, не превратится в работу против сил трения. В результате состав с прицепленным вагоном будет двигаться как одно целое с той же самой скоростью U.

Определим скорость U после сцепления. Для этого применим закон сохранения импульса в проекции на направление движения: , т. е. импульс скатывающегося вагона до сцепления равен суммарному импульсу вагона с составом после сцепления. Отсюда скорость движения состава после сцепления будет равна Совместное движение вагонов после сцепления является признаком неупругого удара. При сцеплении вагонов часть кинетической энергии накатывающегося вагона превращается в энергию сжатия пружин автосцепок, а часть в работу против сил трения в поглощающих механизмах автосцепок и сил трения при качении колес. Если сцепление вагонов произошло, то потери кинетической энергии частично превратятся в потенциальную энергию сжатых пружин автосцепок, а остальная часть энергии рассеется в виде теплоты в окружающее пространство.

Потери кинетической энергии в процессе сцепления вагонов: Если масса состава велика, то налетающий вагон практически остановится после сцепления и вся кинетическая энергия будет потеряна. Если сцепляется один вагон такой же массы, как и накатывающийся, то потери энергии на сцепление равны половине кинетической энергии. Если накатывается сцеп из нескольких вагонов на один вагон, то скорость после сцепления изменится незначительно и потери энергии будут незначительными. На практике для надежности сцепления с составом скорость порожних вагонов после скатывания с сортировочной горки устанавливается более высокой, чем груженых. Если сцепление вагонов не произошло, пружины будут отталкивать выгоны друг от друга. Взаимодействие будет происходить как при упругом ударе. При этом энергия деформации пружин автосцепок превратится в кинетическую энергию разъезжающихся вагонов. Если сталкиваются два одинаковых вагона, то движущийся после удара вагон останавливается, а стоящий начинает двигаться с той же скоростью. Если вагон накатывается на состав большой массы, то после удара он откатывается назад практически с такой же скоростью.

Рекуперация энергии При торможении поезда перед остановкой или при движении поезда вниз по затяжному спуску с возрастанием скорости выше расчетной желательно, чтобы часть или вся механическая энергия поезда снова превратилась в электрическую энергию и вернулась в контактную сеть, либо энергию аккумулировать. Процесс возврата энергии, потребленной локомотивом обратно источнику энергии через контактную сеть, называется рекуперацией энергии. Рассмотрим движение поезда массой M вниз по спуску высотой над некоторым уровнем отсчета. Скорость движения поезда изменяется от начальной до конечной скорости. Так как при движении поезда действует сила сопротивления, механическая энергия не сохраняется, а частично превращается во внутреннюю энергию, в теплоту. В замкнутой системе тел «поезд – Земля» выполняется закон сохранения механической энергии: начальная потенциальная и кинетическая энергии поезда в исходной точке при движении превращаются в работу против сил трения качения на пути S, в работу вращения якорей тяговых двигателей в режиме генерации электроэнергии W; в конце спуска поезда остается кинетическая и потенциальная энергии при высоте конечной точки:

Откуда энергия, которую можно отдать в контактную сеть При торможении на горизонтальном участке ( рекуперации может быть получена за кинетической энергии. счет ), энергия уменьшения При движении с постоянной скоростью на спуске ( ), энергия рекуперации может быть получена за счет уменьшения потенциальной энергии поезда, кроме потерь механической энергии на работу сил трения. Таким образом, применение рекуперации энергии является выгодным для электропоездов. Экономия электроэнергии может достигать 20 %. Не истираются тормозные колодки, колеса и рельсы.

Работа и мощность двигателей в железнодорожном транспорте Мощность, развиваемая локомотивом, равна произведению силы тяги на скорость движения. При движении локомотива в режиме постоянной силы тяги, мощность растет пропорционально скорости движения, и наоборот, при движении локомотива в режиме постоянной мощности сила тяги с ростом скорости уменьшается. Это объясняется тем, что сила отталкивания колесом убегающего назад рельса уменьшается с увеличением скорости рельса. Рассмотрим зависимость мощности и совершаемую тяговыми двигателями работу от режима движения поезда на перегоне между станциями. 1. Режим разгона при трогании. Будем считать, что сила тяги – постоянна и близка к предельной силе сцепления ведущих колес локомотива с рельсами. Движение при постоянной силе тяги является равноускоренным. Предельная сила тяги будет определяться: , где m – масса локомотива - коэффициент сцепления

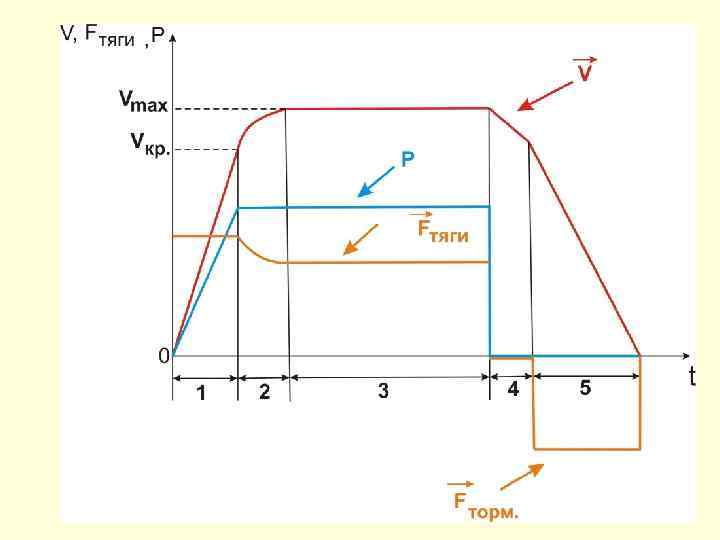
В идеальном случае бесступенчатого плавного регулирования мощность растет прямо пропорционально скорости и времени движения: Мощность тяговых двигателей увеличивают переключением двигателей с последовательного соединения на параллельно-последовательное и параллельное, а также в промежутках между переключениями с помощью пускового реостата. Поэтому регулирование получается ступенчатым. На практике мощность увеличивают таким образом, чтобы не допустить буксования. Равноускоренное движение при разгоне происходит до тех пор, пока при некоторой скорости, которая называется критической, мощность тяговых двигателей не достигнет номинального значения. После этого движение переходит в режим движения с постоянной мощностью. Определим критическую скорость:

Работа тяговых двигателей в рассмотренном режиме превращается в кинетическую и потенциальную энергии поезда и работу против сил сопротивления. На графике зависимости мощности от времени работа равна площади треугольника, то есть , где t - время разгона 2. Режим разгона при постоянной мощности. Как было показано выше, под действием силы тяги поезд движется равноускоренно. Скорость поезда постепенно увеличивается, а сила тяги уменьшается, т. е. Сила тяги в этом режиме ограничена по мощности. Значит, ускорение становится все меньше и, наконец, скорость достигает своего максимального значения. Когда сила тяги будет равна силе сопротивления, режим разгона закончится т. е. и Работа тяговых двигателей в режиме разгона при постоянной мощности будет определяться как произведение номинальной мощности на время движения, то есть

3. Режим равномерного движения с максимальной скоростью. При данном режиме ускорение отсутствует, так как сила тяги компенсирует силу сопротивления движению. Движение происходит при постоянной номинальной мощности тяговых двигателей и достигает наименьшего значения. Максимальная скорость движения поезда будет зависеть от номинальной мощности и силы тяги. 4. Режим выбега Выбег (движение накатом) – это движение поезда с отключенными тяговыми двигателями и без применения тормозов. Режим выбега применяется для снижения скорости перед активным торможением. При данном режиме тяговые двигатели отключены. Кинетическая энергия уменьшается и превращается в работу против силы сопротивления и скатывающей силы: , где i - уклон дороги Если движение происходит не на подъеме, а на спуске , то уклон отрицателен и становится больше, чем коэффициент трения качения. В этом случае режим выбега не осуществим.

5. Режим торможения. Применяется для остановки поезда. Тяговые двигатели отключены. Включена тормозная система локомотива или всего поезда. Для всех тормозящих колес сила торможения равна сумме сил торможения колес и регулируется давлением воздуха в тормозных цилиндрах. В случае экстренного торможения сила торможения равна произведению коэффициента сцепления на силу тяжести поезда: или при торможении только одним локомотивом: Помогают торможению поезда сила сопротивления и скатывающая сила при движении на подъеме. При этом кинетическая энергия уменьшается до нуля в момент остановки, превращаясь в работу против сил сопротивления и, рассеивается в виде теплоты в колодках, колесах или окружающем пространстве. Работа при торможении будет определяться:

Определим тормозной путь до остановки поезда, используя формулу для вычисления предельной силы торможения, получим: Тормозной путь при торможении поезда только локомотивом будет определяться: От эффективности и надежности торможения зависит безопасность движения, а также производительность перевозок.

Динамика вращательного движения Момент силы относительно произвольного центра Как известно из кинематики вращательного движения , Запишем второй закон И. Ньютона, перейдем от линейных величин к угловым: (*) умножим (*) векторно на : , где - псевдовектор, направление которого совпадает с направлением поступательного движения правого винта при его вращении от к. Модуль момента силы определяется: , где - угол между и ; - плечо силы (кратчайшее расстояние между линией действия силы и точкой О. Момент силы относительно произвольного центра будет определяться: Момент силы – физическая векторная величина, являющаяся мерой взаимодействия тел при вращательном движении и численно равная векторному произведению. Это аналог силы.

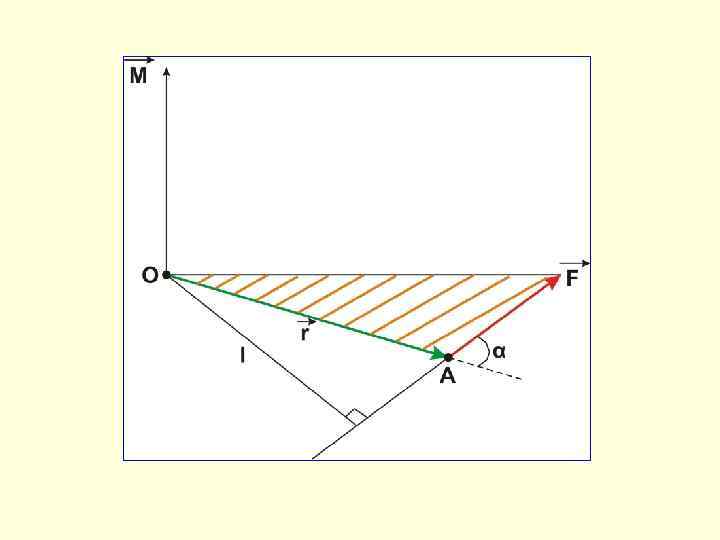
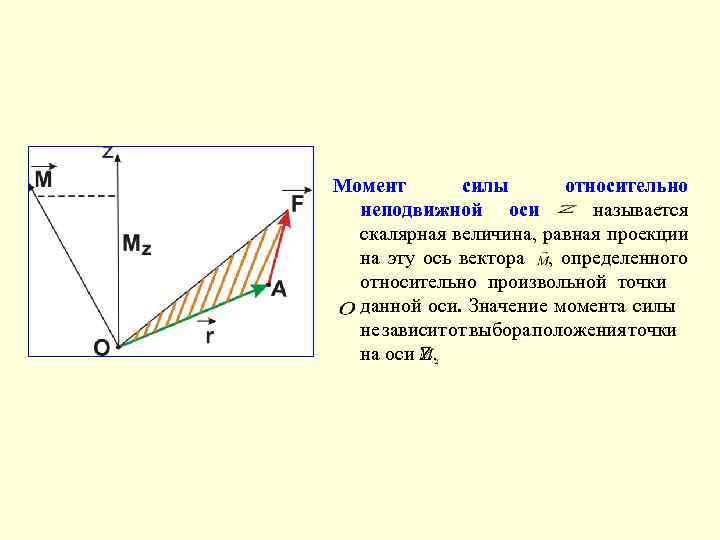Момент силы относительно неподвижной оси называется скалярная величина, равная проекции на эту ось вектора , определенного относительно произвольной точки данной оси. Значение момента силы не зависит от выбора положения точки на оси Z.

Момент инерции материальной точки – физическая скалярная величина, являющаяся мерой инертности при вращательном движении и численно равная произведению массы на квадрат расстояния до центра вращения. Это аналог массы. – момент инерции Если ось Z совпадает с главной осью инерции, проходящей через центр масс, то имеет место равенство, представляющее собой второй закон Ньютона для вращательного движения материальной точки: Сопоставим формулу второго закона Ньютона для поступательного движения материальной точки с полученной формулой для вращательного движения: Поступательное движение Вращательное движение

Момент импульса материальной точки Обозначим произведение , тогда - момент импульса Момент импульса материальной точки – векторная физическая величина, являющаяся мерой вращательного движения тел и численно равная векторному произведению. , где - псевдовектор, направление которого совпадает с направлением поступательного движения правого винта при его вращении от к. Модуль вектора момента импульса равен: , где - угол между векторами и ; - плечо вектора относительно точки О. Момент импульса относительно неподвижной оси Z называется скалярная величина, равная проекции на эту ось вектора момента импульса, определенного относительно точки О данной оси. Момент импульса не зависит от положения точки О на оси Z. уравнение динамики вращательного движения твердого тела: производная момента импульса твердого тела относительно оси равна моменту сил относительно той же оси

Закон сохранения момента импульса замкнутой системы Рассмотрим случай, когда материальная точка совершает вращательное движение под действием центральной силы. Если момент внешних сил равен нулю, тогда получим: Значит, Момент импульса материальной точки движущейся под действием центральной силы есть величина постоянная. Следствия: 1. Так как момент импульса – векторная величина, то траектория точки – плоская кривая. Вектор в каждый момент времени перпендикулярен к плоскости, образованной векторами и. Если , эта плоскость будет фиксированной. Таким образом, при движении частицы в центральном поле сил ее радиус-вектор остается все время в одной плоскости. В этой же плоскости лежит все время вектор. 2. Если , то. 3. - траектория точки – эллипс

Рассмотрим участок траектории движения частицы. За время dt радиус-вектор частицы описывает заштрихованную площадь d. S. Эта площадь равна половине площади параллелограмма, построенного на векторах и. Таким образом, площадь заштрихованного треугольника равна: Площадь, описываемая радиус-вектором частицы в единицу времени, называется секториальной скоростью. При секториальная скорость частицы – есть величина постоянная. Если мы имеем систему, состоящую из n – материальных точек, тогда полный импульс системы будет определяться: При этом суммарный момент всех внутренних сил равен нулю, то есть Если система является замкнутой, то внешними силами можно пренебречь, значит, суммарный момент импульса замкнутой системы материальных точек есть величина – постоянная.

Применение закона сохранения момента импульса 1. В спорте. Гимнасты при поворотах тела в воздухе, в фигурном катании для увеличения угловой скорости. 2. Образование воронок в воде, завихрений в воздухе.

Связь законов сохранения с фундаментальными свойствами пространства и времени. Роль законов сохранения в физике Время однородно – закон сохранения энергии. Пространство – однородно – закон сохранения импульса. Пространство изотропно – закон сохранения момента импульса Таким образом, законы сохранения – отражение свойств пространства и времени, это фундаментальные законы природы, они имеют большое методологическое значение.

Динамика твердого тела Основные понятия Абсолютно твердым телом называют тело, при движении которого расстояние между любыми его двумя точками не меняется. Поступательным называется такое движение абсолютно твердого тела, при котором прямая, соединяющая две любые его точки перемещается параллельно самой себе. Вращательным называется такое движение абсолютно твердого тела, при котором все точки тела описывают концентрические окружности (имеют общий центр). Плоским движением называется такое движение абсолютно твердого тела, при котором все точки тела перемещаются в параллельных плоскостях. Геометрическое место точек не участвующих во вращении называется осью вращения. Плоскость, перпендикулярная оси вращения называется плоскостью вращения.

Рассмотрим движение цилиндра, катящегося без скольжения по плоскости. Его можно рассматривать как поступательное движение со скоростью и одновременное вращение с угловой скоростью вокруг оси О, либо как поступательное движение со скоростью и вращение с той же угловой скоростью вокруг оси , либо, как одно только вращение с той же угловой скоростью вокруг оси. Назвав систему отсчета, относительно которой мы рассматриваем сложное движение твердого тела, неподвижной, движение тела можно представить как вращение с угловой скоростью в системе отсчета, которая движется относительно неподвижной системы поступательно со скоростью. Линейная скорость точки с радиус-вектором, обусловленная вращением твердого тела будет иметь вид: радиусвектором, обусловленная вращением твердого тела Тогда скорость точки при сложном движении:

Элементарное перемещение твердого тела при плоском движении всегда можно представить как поворот вокруг некоторой оси, называемой мгновенной осью вращения. Эта ось может лежать в пределах тела, либо вне его. В нашем примере мгновенная ось совпадает с линией касания цилиндра с плоскостью. При качении цилиндра мгновенная ось перемещается как по плоскости, так и по поверхности цилиндра. Число степеней свободы – это число возможных движений тела. Или Число степеней свободы – это число независимых координат, с помощью которых может быть задано положение тела в данный момент времени. Ограничения, накладываемые на траекторию движения тела называются связями, а движение без ограничений – называется свободным.

Кинетическая энергия вращающегося тела. Момент инерции и момент импульса твердого тела Пусть некоторое тело В вращается около неподвижной оси, проходящей через точку О и направленной перпендикулярно плоскости чертежа. Разобьем все тело на отдельные весьма малые части, массы которых обозначены Их линейные скорости а радиусы Полная кинетическая энергия тела будет равна Если, пользуясь формулой , выразив линейную скорость каждой точки через угловую, получим

Величина, равная сумме произведений масс отдельных частиц тела на квадраты их расстояний до оси вращения, носит название момента инерции тела относительно этой оси. Момент инерции обозначается буквой J, тогда формула запишется в виде Кинетическая энергия вращающегося тела относительно неподвижной оси равна половине произведения его момента инерции относительно этой оси на квадрат угловой скорости. Формула аналогична формуле кинетической энергии поступательного движения. Момент инерции тела аналогичен массе тела и характеризует инертность тела при вращательном движении. Роль линейной скорости играет угловая скорость.

Найдем момент инерции однородного полого цилиндра или обруча относительно его геометрической оси, считая, что вся его масса сосредоточена на ободе. Разобьем его на отдельные части и по формуле: Найдем момент инерции. Так как все частицы расположены на одинаковом расстоянии от оси, равном радиусу r цилиндра, то можно вынести за скобку, тогда Но сумма масс всех частиц цилиндра равна его массе m. Следовательно, Значительно труднее найти момент инерции других тел, частицы которых находятся на разных расстояниях от оси вращения. Математика с помощью интегрального исчисления позволяет вычислить моменты инерции различных тел определенной геометрической формы.

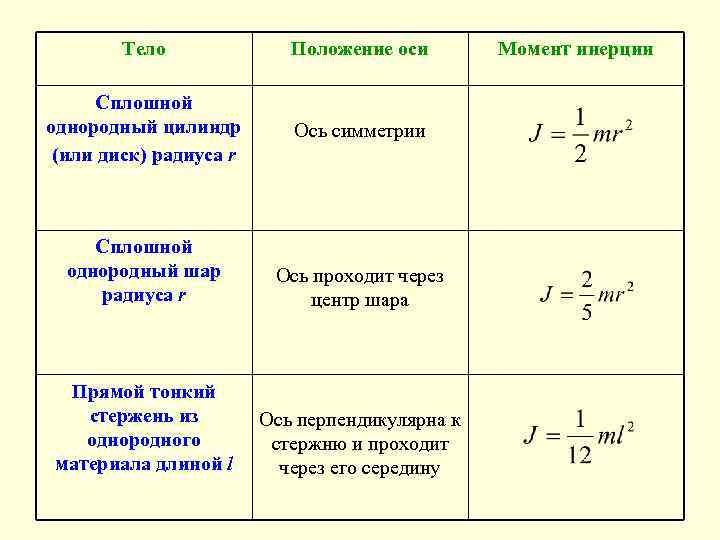Тело Положение оси Сплошной однородный цилиндр (или диск) радиуса r Ось симметрии Сплошной однородный шар радиуса r Ось проходит через центр шара Прямой тонкий стержень из однородного материала длиной l Ось перпендикулярна к стержню и проходит через его середину Момент инерции

Моменты инерции тел, приведенные в таблице, даны относительно осей, проходящих через центры инерции (центры масс) соответствующих тел. Чтобы найти момент инерции тела относительно произвольной оси, надо к моменту инерции относительно оси, проходящей через центр инерции на расстоянии от произвольной оси и параллельной заданному направлению прибавить массу m тела, умноженную на квадрат расстояния между осями. Полная кинетическая энергия катящегося тела, например, цилиндра, складывается из энергий его поступательного и вращательного движений: - угловая скорость цилиндра, вращающегося вокруг своей геометрической оси; - линейная скорость поступательного перемещения самой оси.

Законы Ньютона для вращательного движения твердого тела Вокруг неподвижной оси О может вращаться вал К. Пусть к его ободу приложена постоянная касательная сила F. Если за время t точка приложения этой силы перемещается на расстояние S, то работа силы F будет равна При отсутствии сопротивлений работа А равна изменению кинетической энергии вала, так как вал под действием постоянной силы приходит в равноускоренное вращательное движение: где и - угловые скорости вала соответственно до начала действия силы F и через время t. Расстояние , пройденное точкой приложения силы, согласно формуле точек обода вала, т. е. равно перемещению

Угловой путь равен произведению средней угловой скорости время движения t. Так как или на то Сокращая обе части равенства на имеем Произведение есть момент силы относительно оси вращения Поэтому запишем или но так как отношение Откуда есть угловое ускорение то - второй закон Ньютона для вращательного движения. т. е. угловое ускорение прямо пропорционально моменту силы и обратно пропорционально моменту инерции тела.

• В случае, если на тело не действуют внешние силы, то и т. е. угловая скорость вращающего тела при отсутствии действия на него внешних сил сохраняется неизменной. Сделанное заключение выражает первый закон Ньютона для вращательного движения. • Формула может быть переписана следующим образом: • Величина, равная произведению момента силы на время его действия, носит название импульса момента силы, а произведению момента инерции тела на угловую скорость, - момента импульса (количества движения).

Закон сохранения момента импульса замкнутой системы и его проявление • Если на вращающееся тело не действуют внешние силы, то выражение обращается в нуль. В таком случае и правая часть равенства делается равной нулю, т. е. • Если у вращающегося тела вследствие внутренних причин происходит изменение момента инерции, то выражение сохраняет силу, т. е • Момент импульса вращающегося тела при отсутствии действия на него внешних сил сохраняется неизменным, т. е. при возрастании момента инерции тела уменьшается угловая скорость, а произведение сохраняется постоянным. Это заключение носит название закона сохранения момента импульса. •

Закон сохранения момента импульса успешно иллюстрируется на приборе, предложенном выдающимся русским ученым Н. Е. Жуковским и получившим название скамьи Жуковского. Легкая платформа в форме диска может вращаться с малым трением вокруг вертикальной оси. Человек становится на платформу и вытягивает руки. Его приводят во вращательное движение. При опускании рук вниз уменьшается его момент инерции , а следовательно, возрастает угловая скорость так как произведение Если человек держит в руках массивные гири, то при опускании рук происходит более значительное изменение момента инерции и возрастание угловой скорости еще более заметно. Сделанное заключение для одного тела может быть распространено и на систему тел. Сумма моментов импульсов всех тел замкнутой системы сохраняется неизменной, т. е.

Таблица соотношения характеристик поступательного и вращательного движений твердого тела Поступательное движение Вращательное движение Мера инертности m J Мера взаимодействия Мера механического движения Второй закон Ньютона

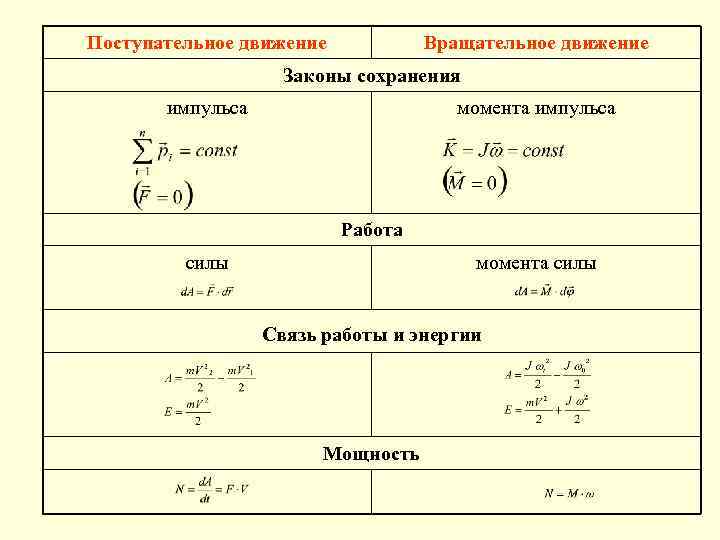Поступательное движение Вращательное движение Законы сохранения импульса момента импульса Работа силы момента силы Связь работы и энергии Мощность

Свободные оси вращения. Устройство гироскопа. Для того чтобы сохранить положение оси вращения твердого тела с течением времени неизменным, используют подшипники, в которых она удерживается. Существуют оси вращения тел, которые не изменяют своей ориентации в пространстве без действия на нее внешних сил. Такие оси называются свободными осями вращения. В любом теле существуют три взаимно перпендикулярные оси, проходящие через центр масс тела, которые могут служить свободными осями. Они называются главными осями инерции тела). Например, главные оси инерции однородного прямоугольного параллелепипеда проходят через центры противоположных граней. Свойство свободных осей сохранять свое положение в пространстве широко применяется в технике. Гироскопы – массивные однородные тела, вращающиеся с большой угловой скоростью около своей оси симметрии, являющейся свободной осью.

Так как трение в подшипниках мало, то, пока гироскоп неподвижен, его оси можно придать любое направление. Если начать гироскоп быстро вращать и поворачивать его подставку, то ось гироскопа сохраняет свое положение в пространстве неизменной. Это объясняется с помощью основного закона динамики вращательного движения. Чтобы ось гироскопа изменила свое направление в пространстве, необходимо, чтобы момент внешних сил не был равен нулю. Это явление в физике называется гироскопическим эффектом. Если ось гироскопа закреплена подшипниками, то из-за гироскопического эффекта возникают гироскопические силы, действующие на опоры, в которых вращается ось гироскопа. Гироскопы применяют в различных навигационных приборах, а также для поддержания заданного направления движения транспортных средств. Впервые гироскоп применил Ж. Фуко для объяснения доказательства вращения Земли.

Движение колеса вагона б) качение представляет собой вращение вокруг мгновенной оси; мгновенная ось вращения проходит через точки касания колесной пары с рельсами. Для колеса угловая скорость равна: При движении вагона его колеса катятся по рельсам. Качение можно представить двумя способами: а) точки колеса участвуют в двух видах движения – перемещаются поступательно вместе с вагоном со скоростью и вращаются относительно оси колеса с угловой скоростью ; точка касания колеса с рельсом должна быть неподвижна относительно рельса, если нет проскальзывания. Из предложенного способа следует, что скорости поступательного и вращательного движений точки касания равны (см. рис. ) и противоположно направлены, то есть

Ускорение точек колеса определяется векторной суммой переносного ускорения, равного ускорению оси колеса или вагона, касательного и нормального ускорений относительно оси: При качении колеса точки поверхности бандажа движутся относительно рельса по криволинейной траектории. Уравнение траектории можно представить геометрически как координату некоторой точки D в зависимости от угла поворота колеса. Найдем абсциссу и ординату точки: - угол поворота колеса относительно оси. Эта кривая в геометрии называется циклоидой. Расстояние, проходимое колесом за полный оборот, равно .

Колебания и волны Основные характеристики механических колебаний Колебательным называется такой процесс, при котором материальная точка (тело) периодически, через равные промежутки времени возвращается к началу координат. Колебательное движение очень распространено в природе и технике. Движение маятника в часах, поршня в цилиндре насоса, двигателя внутреннего сгорания, вибрация мостов, дрожание струн в музыкальных инструментах, качания вагона на пружинах. При этом колебания могут быть как полезными (работа часов) так и вредными (колебания моста при движении по нему поезда, вибрация крыльев самолета при его полете). Поэтому важно правильно понимать природу колебательных процессов. Теория колебаний получила широкое применение в работах П. Н. Лебедева, Л. И. Мандельштама, А. Г. Столетова и др. Физическая природа колебаний весьма разнообразна. Выделяют четыре типа колебаний: Свободные колебания – совершаются за счет первоначально сообщенной энергии при отсутствии внешних воздействий на колебательную систему (колебания шарика, подвешенного на нити – математический маятник; колебания тела около неподвижной горизонтальной оси – физический маятник; колебания подвешенного к пружине груза – пружинный маятник).

Вынужденные колебания – совершаются за счет внешней периодически изменяющейся силы (колебания вагона в результате прохождения колесами стыков рельс). Автоколебания – колеблющаяся система сама управляет внешним воздействием (маятник наручных механических часов получает толчки в определенные моменты времени за счет закрученной пружины). Параметрические колебания – периодическое изменение, каких либо параметров колеблющейся системы (например, длины маятника).

Рассмотрим основные характеристики колебательного процесса: Период – время, в течение которого колебательная система совершает одно полное колебание. Обозначается T, измеряется в секундах (с). Частота – число колебаний, совершаемых в единицу времени. Обозначается. Измеряется в герцах (Гц). Пусть за время t колебательная система совершает N колебаний, тогда Амплитуда – максимальное отклонение тела от положения равновесия. Обозначается A. Измеряется в единицах длины (см, м, мм). Фаза – величина, измеряемая долей периода, прошедшей от начала колебания. Обозначается. Безразмерная величина.

Гармонические колебания. Уравнение гармонических колебаний Простейшим типом колебаний являются гармонические колебания. Гармонические колебания – это колебания, при которых колеблющаяся величина изменяется со временем по закону синуса или косинуса. Гармонические колебания описываются уравнением: где - смещение, A – амплитуда, - круговая (циклическая частота), - начальная фаза колебаний. Запишем выражение для скорости и ускорения колеблющейся материальной точки. Для этого найдем первую и вторую производную по времени от уравнения гармонических колебаний Знак «-» в формуле означает, что ускорение направлено в сторону, противоположную смещению.

Рассмотрим, как изменяются с течением времени величины. Составим таблицу, полагая, что. t x V 0 ωA 0 T/4 A 0 T/2 0 -ωA ¾T -A 0 T 0 ωA рисунке: a 0 Зависимости x и V от t графически представлены на 0 0 Таким образом, скорость имеет максимальное значение, когда гармонически колеблющаяся точка проходит положение равновесия, а ускорение максимально в ее крайних положениях.

Найдем силу, под влиянием которой точка совершает гармоническое колебание, используя второй закон И. Ньютона: Обозначим: Силу, вызывающую гармоническое колебание, называют возвращающей силой. Из уравнения получаем динамическое определение гармонического колебания: гармоническое колебание есть колебание точки около среднего положения под действием силы, пропорциональной смещению и направленной в сторону среднего положения.

Энергия колеблющегося тела Колеблющаяся материальная точка обладает кинетической энергией, которая определяется по формуле: Так, как скорость равна , то В крайних положениях кинетическая энергия равна нулю, в среднем положении она имеет максимальное значение. Колеблющаяся точка будет обладать и потенциальной энергией, смещенной относительно положения равновесия на величину x ; измеряется работой внешних сил, которая была произведена для того, чтобы вызвать это смещение, то есть

Потенциальная энергия колеблющейся точки максимальна в крайних положениях и равна нулю в положении равновесия. Полная энергия: Заменяя , получим: Таким образом, энергия тела, совершающего гармоническое колебание, прямо пропорциональна массе тела, квадрату амплитуды и квадрату частоты колебаний.

Маятник. Виды маятников Маятник – твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной оси. Принято различать пружинный, математический и физический маятники. Вид маятника Определение пружинный Тело Рисунок Основные формулы для расчета… массой m подвешенное на абсолютно упругой пружине и совершающее гармонические колебания под действием упругой силы. математиче ский Величина упругой силы: Уравнение движения маятника: . Циклическая частота: Период: Потенциальная энергия: Идеализированная система, состоящая из тела массой m, подвешенного на нерастяжимой нити и совершающая колебания под действием силы тяжести. Момент возвращающей силы: (при Циклическая частота: Период: Момент инерции: где l - длина маятника. )

Вид маятника Определени е физический Любое твердое тело, свободно вращающееся вокруг неподвижной горизонтально й оси, не проходящей через его центр тяжести Рисунок Основные формулы для расчета… Момент возвращающей силы где I - момент инерции маятника относительно оси, проходящей через точку подвеса; l - расстояние между точкой подвеса и центром масс маятника; возвращающая сила, где «-» показывает, что и всегда противоположны; соответствует малым отклонениям маятника от положения равновесия. Циклическая частота: Период: где - приведенная длина Приведенная длина – это длина такого математического маятника, период колебаний которого совпадает с периодом колебаний физического маятника.

Сложение однонаправленных колебаний одинаковой частоты Пусть материальная точка одновременно участвует в двух гармонических колебаниях, происходящих по одной прямой. Уравнения этих колебаний будут иметь вид: Амплитуды и начальные фазы этих колебаний разные, круговая частота одна и та же, так как период одинаковый. Результирующее колебание равно сумме колебаний, т. е. Заменяя и их выражениями и применяя известные тригонометрические формулы, получаем Обозначим: Из уравнения следует: или Таким образом, в результате сложений двух гармонических колебаний одного периода, происходящих по одной прямой, получается гармоническое колебание такого же периода, происходящее по этой же прямой.

Амплитуду и начальную фазу результирующего колебания можно найти при помощи системы уравнений. Поделим почленно эти два уравнения Возведем обе части уравнения в квадрат и сложим их, получим: или Анализ уравнения: амплитуда результирующего колебания зависит от разности фаз складываемых колебаний. 1. Амплитуда будет максимальна и равна сумме амплитуд, когда т. е. когда разность фаз равна четному числу : , где , 2. Амплитуда будет минимальна и равна разности амплитуд, если разность фаз складываемых колебаний равна нечетному числу : , где

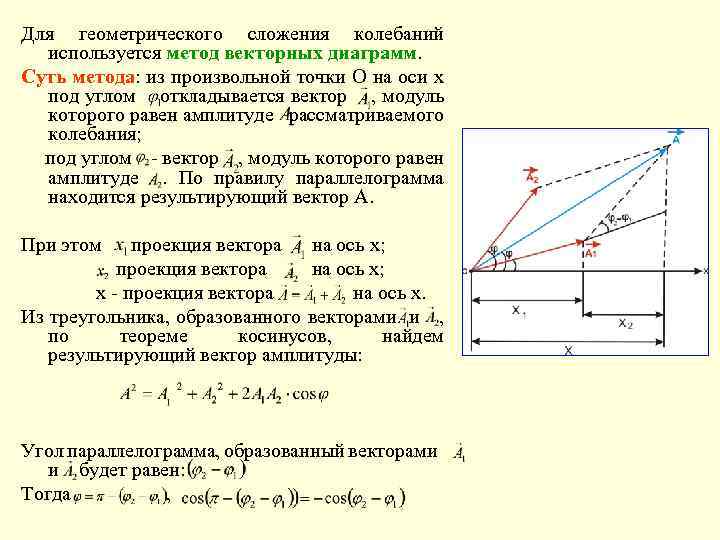Для геометрического сложения колебаний используется метод векторных диаграмм. Суть метода: из произвольной точки О на оси х под углом откладывается вектор , модуль которого равен амплитуде рассматриваемого колебания; под углом - вектор , модуль которого равен амплитуде. По правилу параллелограмма находится результирующий вектор A. При этом проекция вектора на ось x; x - проекция вектора на ось x. Из треугольника, образованного векторами и , по теореме косинусов, найдем результирующий вектор амплитуды: Угол параллелограмма, образованный векторами и будет равен: Тогда ,

Сложение взаимно перпендикулярных гармонических колебаний Пусть складываются два взаимно перпендикулярных колебания одинакового периода. Их уравнения будут иметь вид Траектория результирующего движения будет расположена в прямоугольнике, стороны которого параллельны осям координат и равны и. Для того, чтобы получить уравнение траектории, надо из уравнений исключить время. Рассмотрим частные случаи: 1. Пусть. Поделим почленно уравнения, получим Траектория представляет собой прямую, проходящую в I и III четвертях. 2. Пусть разность фаз колебаний равна , т. е. , Перепишем первое уравнение системы следующим образом: . Поделим почленно уравнения системы, получим: Траектория представляет собой прямую, проходящую во II и IV четвертях.

3. Пусть , . Первое уравнение системы можно представить в виде Система уравнений будет иметь вид: - уравнение эллипса

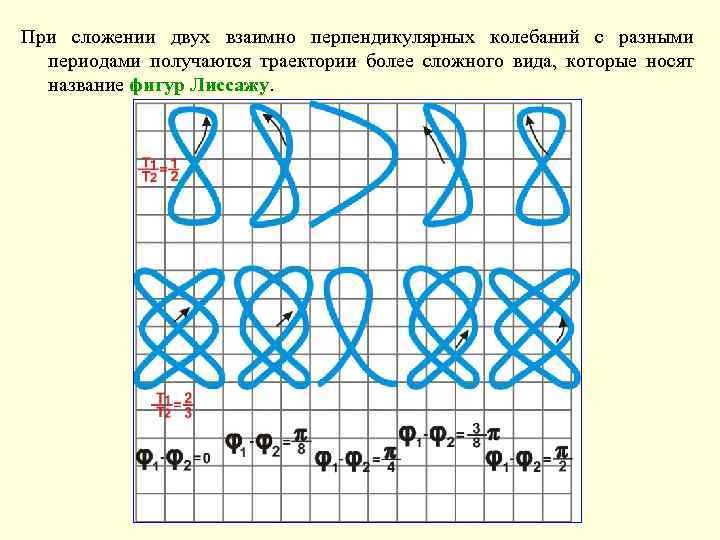При сложении двух взаимно перпендикулярных колебаний с разными периодами получаются траектории более сложного вида, которые носят название фигур Лиссажу.

Биения Рассмотрим сложение колебаний, происходящих по одному направлению с одинаковыми амплитудами, но с разными частотами мало отличающимися друг от друга. Уравнения этих колебаний имеют вид , при этом. Амплитуда результирующего колебания зависит от разности фаз складываемых колебаний, и будет меняться с течением времени. Так как разность фаз складываемых колебаний переменна, то за начало отсчета времени примем тот момент, при котором фазы обоих колебаний одинаковы. В этом случае начальные фазы равны нулю и уравнения примут вид Результирующее смещение x равно: Таким образом, получилось колебание со средней угловой частотой , так как и мало отличаются друг от друга, и медленно меняющейся с течением времени амплитудой A , равной Такие колебания называются биениями.

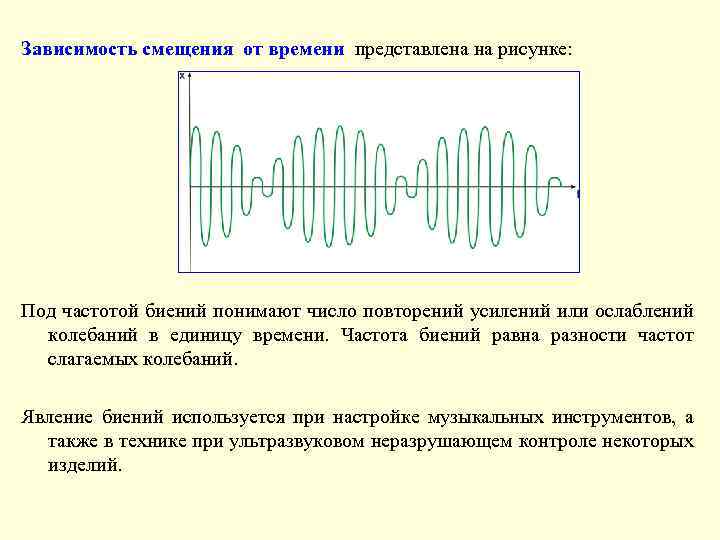Зависимость смещения от времени представлена на рисунке: Под частотой биений понимают число повторений усилений или ослаблений колебаний в единицу времени. Частота биений равна разности частот слагаемых колебаний. Явление биений используется при настройке музыкальных инструментов, а также в технике при ультразвуковом неразрушающем контроле некоторых изделий.

Затухающие и вынужденные колебания вагона Затухающие колебания – это колебания, амплитуда которых со временем уменьшается. Причиной затухания является действие сил сопротивления. Так как избавиться от сил сопротивления невозможно, то собственные колебания тела всегда являются затухающими. Для пружинного маятника массой m, совершающего малые колебания под действием упругой силы равной , сила трения пропорциональна скорости, то есть где r - коэффициент сопротивления. Знак «-» показывает, что сила трения и скорость направлены в противоположные стороны. Тогда, при данных условиях уравнение будет иметь вид: поделим почленно на m обе части уравнения, получим – дифференциальное однородное уравнение второго порядка.

Обозначим: С учетом введенных обозначений, получим – дифференциальное уравнение простейшей колебательной системы с трением. Решением уравнения будет являться уравнение вида: Опыт показывает, что скорость убывания амплитуды со временем пропорциональна самой амплитуде, то есть (*), где - коэффициент затухания, равный Решим уравнение (*), для этого разделим переменные и проинтегрируем:

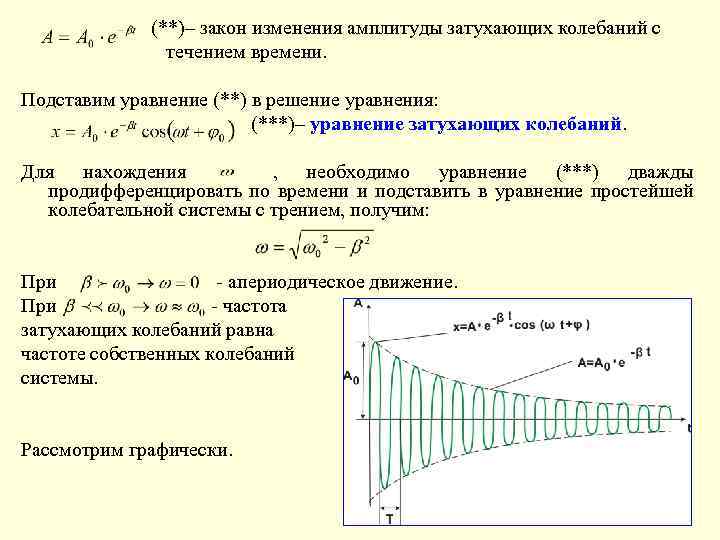(**)– закон изменения амплитуды затухающих колебаний с течением времени. Подставим уравнение (**) в решение уравнения: (***)– уравнение затухающих колебаний. Для нахождения , необходимо уравнение (***) дважды продифференцировать по времени и подставить в уравнение простейшей колебательной системы с трением, получим: При - апериодическое движение. При - частота затухающих колебаний равна частоте собственных колебаний системы. Рассмотрим графически.

1. 2. Параметры, характеризующие затухающие колебания. - коэффициент затухания. - логарифмический декремент затухания (логарифм отношения двух последовательных амплитуд колебаний). 3. Время релаксации - (время, за которое амплитуда колебаний убывает в e раз). – величина, обратная времени, за которое амплитуда убывает в e раз. Покажем, что - величина, обратная числу колебаний, по истечении которых амплитуда убывает в e раз. 4. Добротность - , равна. Добротность пропорциональна числу колебаний, совершаемых системой за время релаксации.

Затухание колебаний для вагона является необходимым, иначе, получив толчок, вагон бы мог совершать колебания сколь угодно долго, пока другой толчок в противофазе не прекратил бы их. На практике для увеличения степени затухания колебаний вагонов и локомотивов применяют амортизаторы. Амортизаторы – это устройства для гашения колебаний. Для гашения колебаний вагона применяются гидравлические амортизаторы, в которых сила сопротивления создается при протекании жидкости через узкое отверстие в поршне гидроцилиндра. Можно гасить колебания и с помощью фрикционных поглощающих механизмов, действие которых основано на трении деталей (например, листов рессор друг о друга) или использовать резиноподобные детали подвески, в которых энергия теряется вследствие внутреннего трения в материале.

Вынужденные колебания – это колебания, происходящие под действием внешней периодически изменяющейся силы. Для того, чтобы колебания были незатухающими, необходимо пополнять потери энергии. Такое пополнение возможно с помощью какого-либо периодически действующего фактора, изменяющегося по гармоническому закону – внешней вынуждающей силы где - частота вынуждающей силы Закон движения для пружинного маятника запишется в виде поделим почленно на m обе части уравнения, получим Используя и , придем к уравнению – дифференциальное уравнение вынужденных колебаний.

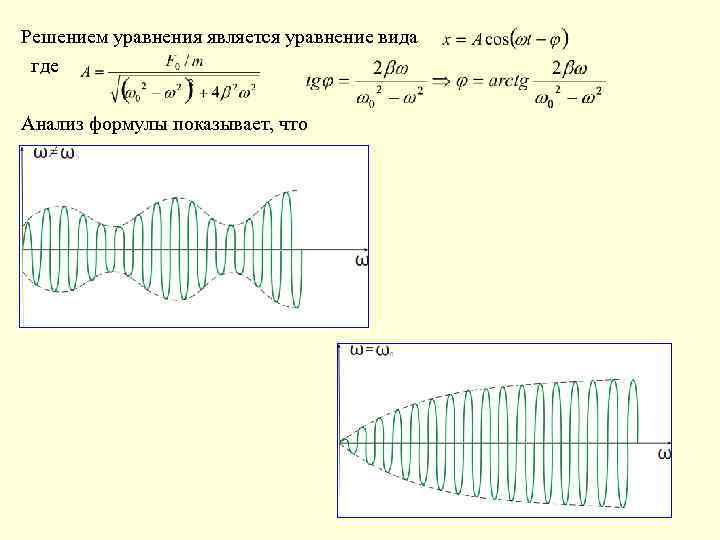Решением уравнения является уравнение вида где Анализ формулы показывает, что

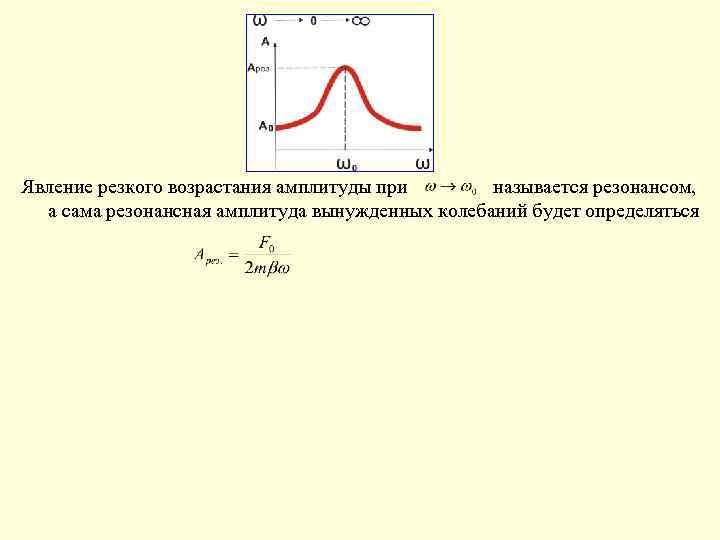Явление резкого возрастания амплитуды при называется резонансом, а сама резонансная амплитуда вынужденных колебаний будет определяться

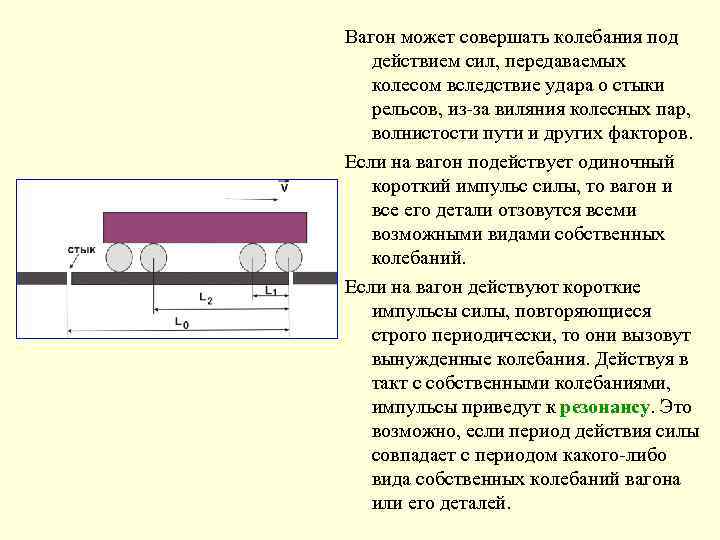Вагон может совершать колебания под действием сил, передаваемых колесом вследствие удара о стыки рельсов, из-за виляния колесных пар, волнистости пути и других факторов. Если на вагон подействует одиночный короткий импульс силы, то вагон и все его детали отзовутся всеми возможными видами собственных колебаний. Если на вагон действуют короткие импульсы силы, повторяющиеся строго периодически, то они вызовут вынужденные колебания. Действуя в такт с собственными колебаниями, импульсы приведут к резонансу. Это возможно, если период действия силы совпадает с периодом какого-либо вида собственных колебаний вагона или его деталей.