Физические основы электроники Часть 1 История развития электроники

Физические основы электроники Часть 1. История развития электроники. Кристаллическая решётка. Зонная теория твёрдого тела. Понятие электронной эмиссии металлов в вакууме.

Литература 1. 2. 3. 4. • Толмачёв В. В. , Скрипник Ф. В. Физические основы электроники. Учебное пособие. - Москва - Ижевск: Институт компьютерных исследований, 2011. - 496 с Россадо Л. Физическая электроника и микроэлектроника. Учебное пособие для вузов. – М. : Высшая школа, 1991. - 352 с Шалимова К. В. Физика полупроводников. Учебник для вузов. - М. : Энергоатомиздат, 1983. - 392 с Электронные приборы. Учебник для вузов. Под ред. Г. Г. Шишкина. - М. : Энергоатомиздат, 1989. - 489 с Егоров, Н. М. Электроника. Версия 1. 0 [Электронный ресурс] : конспект лекций /Н. М. Егоров. – Красноярск : ИПК СФУ, 2008. 2

3

Поколения элементной базы 1. электровакуумные приборы (1904, 1907) 2. дискретные полупроводниковые приборы (1948) 3. интегральные микросхемы (1958) 4. наноэлектроника (198 х) 4

Кристаллическая решётка Бравэ Вектор R = n 1 a+ n 2 b + n 3 c, 1 – простая кубическая, 2 – гранецентрированная кубическая 5

Полупроводники • III, IV, V, VI группах Периодической системы элементов Менделеева: Si, Ge, Ga. As, In. P, Se, Te и другие • внутренние оболочки атомов полностью заполнены электронами • на внешних оболочках располагаются валентные электроны • валентные электроны слабее связаны с ядром, могут легко разорвать связь • валентные электроны обеспечивают тепло- и электропроводность 6

Кристаллическая решётка полупроводников решетка типа алмаза: две гранецентрированые кубические решетки, сдвинутые одна относительно другой на 1/4 главной диагонали • Ковалентные (парноэлектронные) связи 7

Кристаллография. 1. Положение одного из атомов выбирают за начало координат, от которого проводят координатные оси в направлениях основных векторов (a, b, c). 2. Точки пересечения воображаемой кристаллографической плоскости с этими координатными осями выражают целыми числами, приняв за единицу длины основных векторов 3. Величины, обратные этим числам, умножают на их минимальный общий знаменатель, получая простейшую последовательность целых чисел. Эти числа обозначаются h, k, l, и их запись в круглых скобках будет индексами Миллера для данной кристаллографической плоскости. Для рис. 1. 5 получилось 8

Кристаллография. Индекс Миллера (1/1, 1/3, 1/2)*6=(6, 2, 3) 2 9

Крсталлографические плоскости кубической решётки 10

Кристаллическая решётка Ga. As (в плоскости) 11

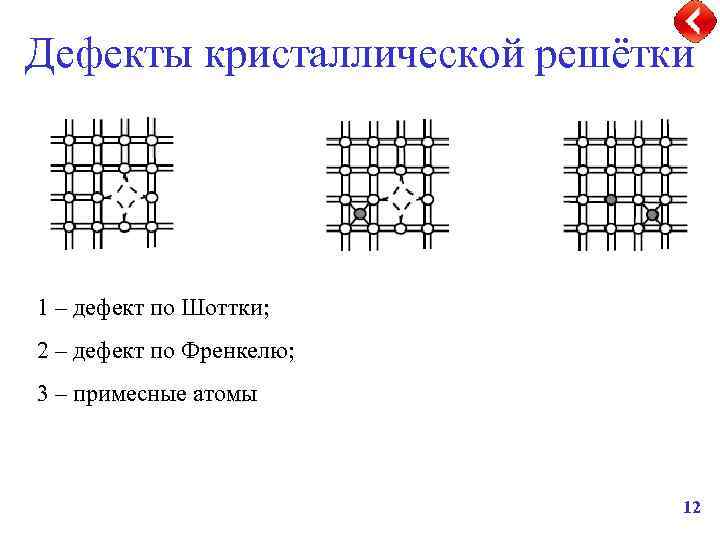Дефекты кристаллической решётки 1 – дефект по Шоттки; 2 – дефект по Френкелю; 3 – примесные атомы 12

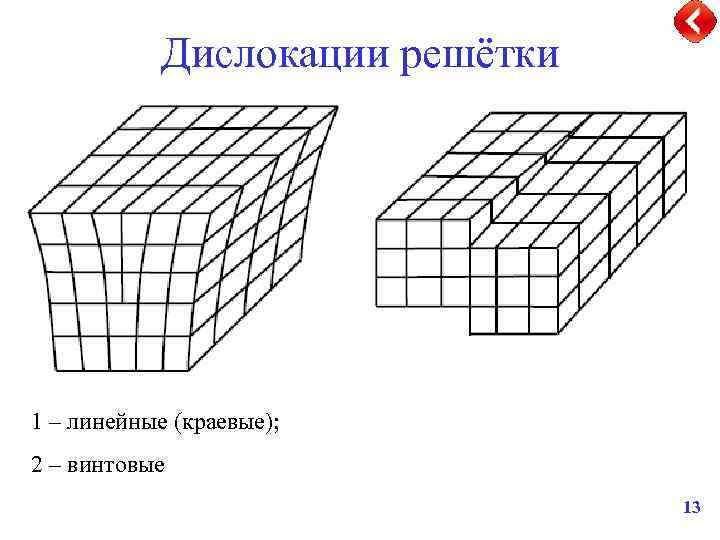Дислокации решётки 1 – линейные (краевые); 2 – винтовые 13

Краевые эффекты решётки • Край – грубое нарушение структуры КР • Восстановление равновесия: – Уплотнение структуры (перестройка поверхности) – Притяжение (адсорбция) чужеродных атомов • Краевая структура отличается от объёмной структуры КР! 14

ЗОННАЯ ТЕОРИЯ ТВЕРДОГО ТЕЛА • Задача - математически описать поведение заряженной частицы (например, электрона) в кристалле. • Математическая модель должна учитывать большинство эффектов, обусловленных влиянием кристаллической решетки. 15

«Падающий электрон» F 1=e 2/r 2 - Кулоновская сила притяжения F 2 =mv 2/r – центробежная сила F 1 = -F 2 v=(e 2/mr)1/2 ~106 м/с Запасённая энергия: E = -e 2/2 r Интенсивность излучения I = 2 e 2 r 2 / 3 C 3 Через τ ≈ r/v*(C/V)3 (τ ≈ 10– 10 c) электрон упадёт на ядро… 16

Квантовая механика • позволяет объяснить закономерности поведения заряженных частиц внутри твердого тела. (Макс Планк, Нильс Бор, Луи де Бройль, Вернер Гейзенберг, Эрвин Шредингер, Вольфганг Паули, Поль Дирак, Энрико Ферми, Макс Борн) 17

Обратная решётка • упорядоченная совокупность точек, представляющая собой безразмерные значения волнового вектора, нормированные к импульсу частицы: k = p/ђ. 18

Волновая теория • Волны Де Бройля (1924): • Уравнение Шредингера (1926) где Ψ(x)– волновая функция электрона; E – кинетическая энергия электрона; V(x) – потенциальная энергия электрона; m – масса электрона. 19

Модель Зоммерфельда Потенциальная энергия электрона в металле: Предполагается, что внутри проводника поля взаимно компенсируются, а на краю есть «ограничивающее» поле 20

Модель Кронига – Пенни Потенциальная энергия электрона в металле (предполагается движение в переменном поле, создаваемом ядрами атомов) Уравнение Шредингера: где V(x) – периодический потенциал; Ψ(x) – волновая функция электрона. 21

Волновые зоны E(k) k 22

Энергетические зоны полупроводника 23

Вероятность заполнения энергетического уровня а)Максвелла-Больцмана б)Ферми-Дирака 24

Зонная диаграмма, функция распределения и концентрация носителей в собственном п/п 25

Зонная диаграмма, функция распределения и концентрация носителей в п/п n-типа 26

Зонная диаграмма, функция распределения и концентрация носителей в п/п p-типа 27

Зонная структура металла и диэлектрика 28

Краевой эффект металл-вакуум • Нет окислов • Нет диффузии • Притяжение ядер уменьшается пропорционально r 2 • Столкновения (с электронами и ядрами) минимальны 29

Электронная эмиссия(1) T 0 T >> T 0 30

Электронная эмиссия(2) U 0=0 + U 0>>0 + 31