ФИЗИЧЕСКАЯ ХИМИЯ ЭКСТРЕМАЛЬНЫХ ВОЗДЕЙСТВИЙ — Газы при высоких

ФИЗИЧЕСКАЯ ХИМИЯ ЭКСТРЕМАЛЬНЫХ ВОЗДЕЙСТВИЙ - Газы при высоких давлениях - Равновесия в гетерогенных системах -Диаграммы состояния - Фазовые переходы - Кинетика гетерогенных реакций

Литература 1. Калашников Я. А. Физическая химия веществ при высоких давлениях. М. , Высшая школа, 1987 2. Циклис Д. С. Плотные газы. М. , Химия, 1977 3. Герасимов Я. И. Курс физической химии. Т. 1. М. , Химия, 1970 4. Вест А. Химия твердого тела. Часть 1. М. , Мир, 1988 5. Третьяков Ю. Д. Твердофазные реакции. М. , Химия, 1978 6. Гоникберг М. Г. Химическое равновесие и скорость реакций при высоких давлениях. М. АН СССР, 1960 7. Учебные материалы на сайте www. chem. msu. ru 8. Варгафтик Н. Б. Справочник по теплофизическим свойствам газов и жидкостей. М. , Наука, 1972

Термодинамические параметры – величины, характеризующие макроскопическое состояние тел объем (v), температура (Т), давление (р), энтальпия (Н), теплоемкость (С) и др. Изменение одних вызывает изменение других (не обязательно всех) Для решения этих уравнений нужна зависимость f(p, V, T)=0 Уравнение состояния: функциональная зависимость между давлением, объемом и температурой Не выводится из основных законов термодинамики! Определяется: - эмпирически (экспериментальное измерение p, V, T) -из теоретических соображений

Идеальные газы p. V=RT - между молекулами газа нет взаимодействия - молекулы являются материальными точками ( имеют бесконечно малый размер) Экспериментально: выполняется только для очень разряженных газов!

Идеальные газы Мольные объемы газов при 1 атм и 273 K (22, 414 л) Газ Vm, л* моль-1 H 2 22, 43 CO 2 22, 26 He 22, 43 N 2 O 22, 25 Ne 22, 42 H 2 O 22, 14 F 2 22, 42 NH 3 22, 08 N 2 22, 40 Cl 2 22, 02 CO 22, 40 SO 2 21, 89 O 2 22, 39 C 4 H 10 21, 50 CH 4 22, 36 O 3 21, 60 Отклонение от идеальности: H 2, He, Ar, N 2, O 2 (низкая температура кипения) – до 2 % при р =10 атм CO 2, SO 2, CH 4 (высокая температура кипения) – > 1% уже при р = 1 атм

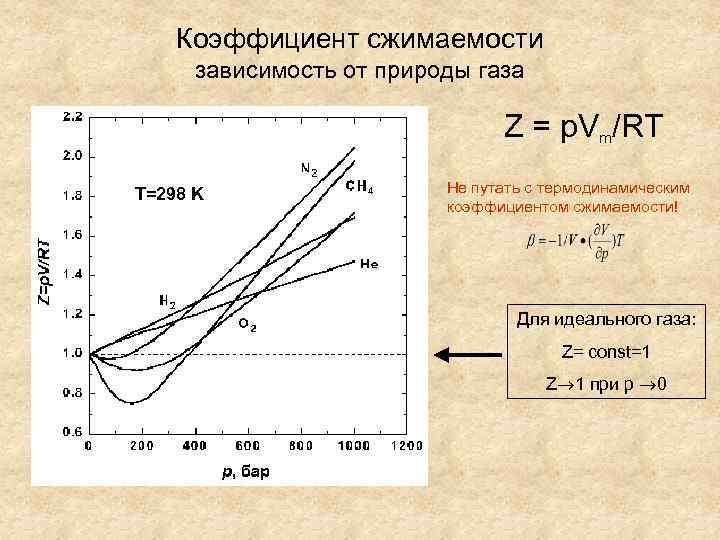Коэффициент сжимаемости зависимость от природы газа Z = p. Vm/RT T=298 K Не путать с термодинамическим коэффициентом сжимаемости! Для идеального газа: Z= const=1 Z 1 при р 0

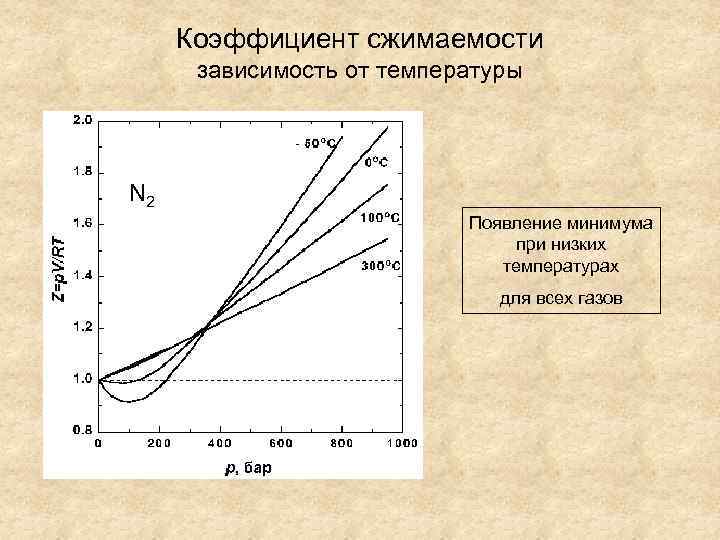Коэффициент сжимаемости зависимость от температуры T=298 N 2 K Появление минимума при низких температурах для всех газов

Критические явления Критические константы газов Газ Vc, мл* моль He 5, 21 2, 27 57, 76 44, 44 26, 9 41, 74 Ar 150, 72 48, 0 75, 25 Kr 209, 4 54, 3 92, 24 Xe 289, 75 58, 0 118, 8 H 2 33, 3 13, 0 65, 0 N 2 126, 1 34, 0 89, 5 O 2 154, 4 50, 5 73, 4 CO 2 304, 2 73, 8 94, 0 CH 4 190, 7 46, 0 99, 0 C 2 H 4 ср. = ( ж + п)/2 = А+ВТ Pc, бар Ne СО 2 Tc, K 282, 4 50, 4 129, 0 Правило Кальете-Матиаса -1

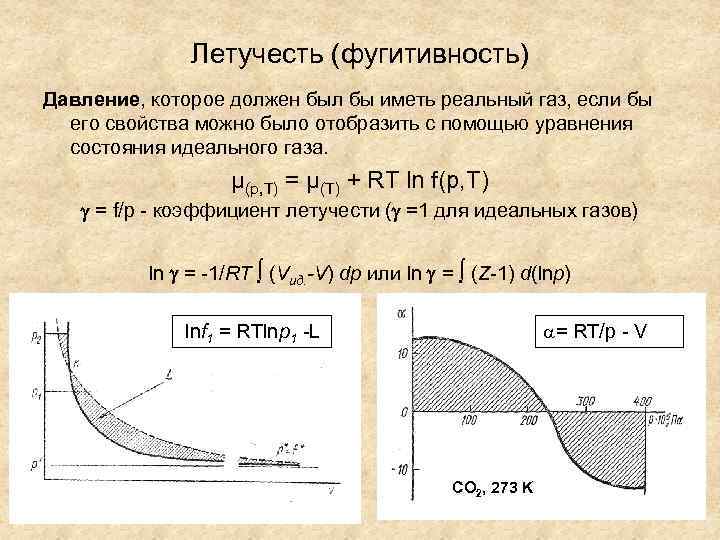Летучесть (фугитивность) Давление, которое должен был бы иметь реальный газ, если бы его свойства можно было отобразить с помощью уравнения состояния идеального газа. μ(p, T) = μ(T) + RT ln f(p, T) = f/p - коэффициент летучести ( =1 для идеальных газов) ln = -1/RT ∫ (Vид. -V) dp или ln = ∫ (Z-1) d(lnp) a= RT/p - V lnf 1 = RTlnp 1 -L CO 2, 273 K

Значения летучести газов р, бар f. CO 2, бар +60 о. С f. Н 2, бар -75 о. С 25 23, 2 25, 4 100 70, 4 107, 3 300 112 380 При р= 1000 бар, Т=0 о. С NH 3 - f = 204 бар СО - f = 2600 бар Значения летучести водорода/азота р, кбар Температура, о. С 25 50 100 3 19/47 16/41 12/36 5 103/645 80/475 51/295 10 2800/171700 1770/89870 832/31570 Плотность (г/см 3) Н 2: жидкий - 0, 071, твердый -0, 081 газ (65 o. C, 15 кбар) - 0. 13

Реальные газы Уравнение Ван-дер-Ваальса 1864 г. , Дюпре: поправка, учитывающая собственный объем молекул p(V-b)=RT 1873 г. , Ван-дер-Ваальс: силы притяжения между молекулами газа пропорциональны r 6 (или V 2) (p + a/V 2)(V-b)=RT a, b –константы, зависящие от природы газа Не зависят от температуры и давления!

Константы Ван-дер-Вальса Газ a, л 2 *бар* моль-2 He 0, 03457 23, 70 NO 1, 358 27, 89 Ne 0, 2135 17, 09 NO 2 5, 354 44, 24 Ar 1, 363 32, 19 H 2 O 5, 536 30, 49 Kr 2, 349 39, 78 H 2 S 4, 490 42, 87 Xe 4, 250 51, 05 NH 3 4, 225 37, 07 H 2 0, 2476 26, 61 SO 2 6, 803 56, 36 N 2 1, 408 39, 13 CH 4 2, 283 42, 78 O 2 1, 378 31, 83 C 2 H 4 4, 530 5, 714 Cl 2 6, 579 56, 22 C 2 H 6 5, 562 63, 80 CO 1, 505 39, 85 C 3 H 8 8, 779 84, 45 CO 2 3, 640 42, 67 C 6 H 6 18, 24 115, 4 b, см 3 * моль-1 Газ a, л 2 * бар* моль-2 b, см 3 * моль-1

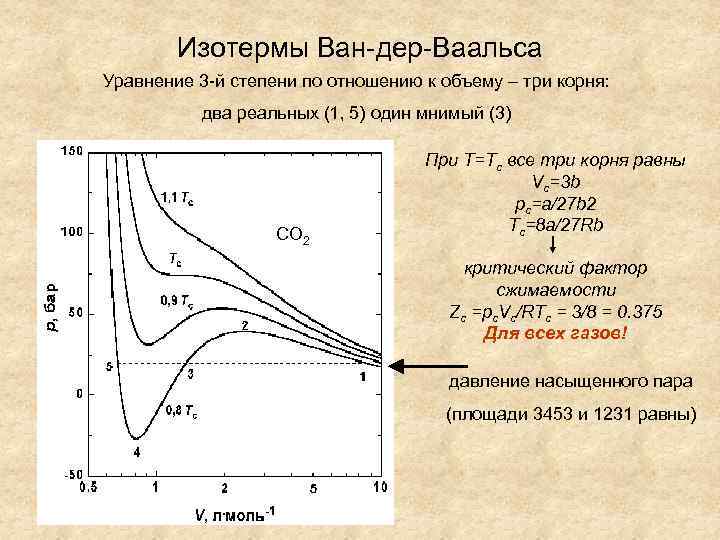Изотермы Ван-дер-Ваальса Уравнение 3 -й степени по отношению к объему – три корня: два реальных (1, 5) один мнимый (3) СО 2 При Т=Тс все три корня равны Vc=3 b pc=a/27 b 2 Tc=8 a/27 Rb критический фактор сжимаемости Zc =pc. Vc/RTc = 3/8 = 0. 375 Для всех газов! давление насыщенного пара (площади 3453 и 1231 равны)

Модификации уравнения Ван-дер-Ваальса Универсальные Уравнение Бертло (p + a'/TV 2)(V - b) = RT Уравнение Битти-Бриджмена p. V 2 = RT[V+B 0(1 -b/V)](1 -c/VT 3) - A 0(1 -a/V) Азот, 0 о. С, 100 МПа p. V/RT= 1. 000 (и. г. ); 2. 442 (В-д-В); 1. 650 (Б); 2. 010 (Б-Б) эксп. 2. 068 Для отдельных газов Уравнение Хеммеса (для водорода) [p + a(p)/va(T)] [v - b(p)] = RT a(p) = exp[a 1+a 2 ln(p)-exp(a 3+a 4 ln(p))] b(p) = biln(p)i (T) = 0 + 1 T + 2 T 2

Вириальное уравнение состояния Вместо минимального числа параметров - бесконечные ряды p. Vm = RT(1 + B 2/Vm + B 3/(Vm)2 +. . . ) или p. Vm = RT (1 + B 2'p + B 3'p 2 +. . . ) Единственное уравнение состояния, имеющее строгую теоретическую основу: вириальные коэффициенты можно выразить через силы межмолекулярного взаимодействия (второй - парные, третий тройные и т. д. ) B 2 /Vm >> B 3 /(Vm)2 >>. . . При низких температурах В 2<0 При высоких температурах В 2 → 0 (проходя через положительный максимум)

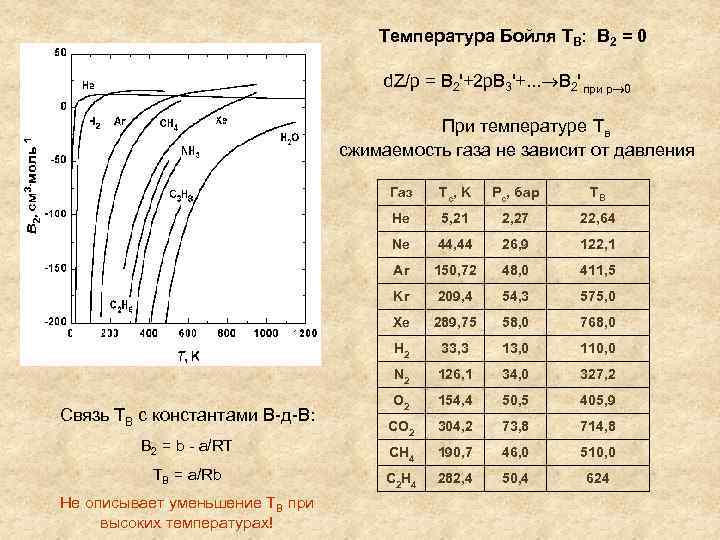Температура Бойля ТВ: В 2 = 0 d. Z/p = B 2'+2 p. B 3'+. . . B 2' при р 0 При температуре Тв сжимаемость газа не зависит от давления Газ 2, 27 22, 64 44, 44 26, 9 122, 1 150, 72 48, 0 411, 5 Kr 209, 4 54, 3 575, 0 Xe 289, 75 58, 0 768, 0 H 2 33, 3 13, 0 110, 0 N 2 Не описывает уменьшение ТВ при высоких температурах! 5, 21 Ar TB = a/Rb ТВ Ne B 2 = b - a/RT Pc, бар He Связь ТВ с константами В-д-В: Tc, K 126, 1 34, 0 327, 2 O 2 154, 4 50, 5 405, 9 CO 2 304, 2 73, 8 714, 8 CH 4 190, 7 46, 0 510, 0 C 2 H 4 282, 4 50, 4 624

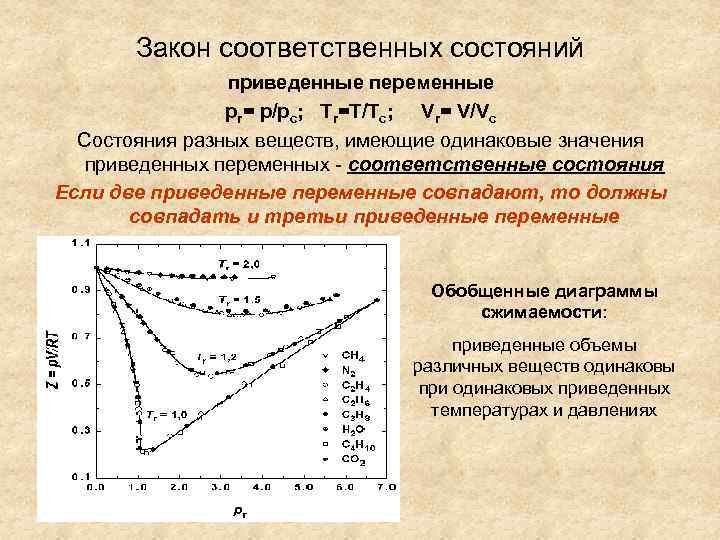Закон соответственных состояний приведенные переменные pr= p/pc; Tr=T/Tc; Vr= V/Vc Состояния разных веществ, имеющие одинаковые значения приведенных переменных - соответственные состояния Если две приведенные переменные совпадают, то должны совпадать и третьи приведенные переменные Обобщенные диаграммы сжимаемости: приведенные объемы различных веществ одинаковы при одинаковых приведенных температурах и давлениях

Квантовые флюиды водород Т 0 с, K 43, 6 p 0 c, бар 20, 5 V 0 c, см 3/моль 51, 5 гелий 10, 47 6, 76 37, 5 T*c = T 0 c/[1+(C 1/MT)] p*c = p 0 c[1+(C 2/MT)] V*c = 0, 292 RT*c/p*c C 1=21, 8 K; C 2=44, 2 K, M - молекулярная масса неон 45, 5 27, 26 40, 3

Газы при сверхвысоких давлениях Уравнение Тейта V = V 0 [1 + C ln (B+p)/(B+p 0)] V 0 - начальный объем при давлении р0, принятом за нуль отсчета Выведено для жидкостей и твердых тел → применимо для сильно сжатых (плотных) газов (р0 ≈ 2 -3 кбар) B = (2760/Tr) -2660 C = 0, 38 - 0, 0594 (1/Tr) Точность (отклонение расчетных значений от экспериментальных) 2 -3% при давлениях до 10 -20 кбар

Смеси газов при высоких давлениях Парциальное давление - давление, которое имел бы чистый компонент, находясь при тех же массе, объеме и температуре, как и в смеси. Парциальный объем - объем, который занимал бы чистый компонент, находясь при таких же массе, давлении и температуре, как и в смеси. Идеальные газы - аддитивность: pi = pχi ; Vi = V χi pc' = Σ χipic Реальные газы: fi = fio χi Фазовые равновесия в системах газ - газ Система азот - аммиак

Баротропное явление Две несмешивающиеся флюидные фазы А и В с разной плотностью При повышении давления может меняться знак соотношения VA/VB→ перераспределение фаз в объеме Пример: р He (Tc =5 K) + H 2 (Tc =33 K) Т=20 K, р= 1 атм Гелий - г (вверху), водород - ж (внизу) Т=20 K, р= 50 атм ρН 2 > ρНe Гелий - г (внизу), водород - ж(вверху)

Газ Vm, л* моль-1 H 2 22, 43 CO 2 22, 26 He 22, 43 N 2 O 22, 25 Ne 22, 42 H 2 O 22, 14 F 2 22, 42 NH 3 22, 08 N 2 22, 40 Cl 2 22, 02 CO 22, 40 SO 2 21, 89 O 2 22, 39 C 4 H 10 21, 50 CH 4 22, 36 O 3 21, 60 Определите факторы сжимаемости (Z = p. Vm/RT) для водорода и аммиака при 1 атм и 273 К. Как они изменятся при повышении температуры при 1 атм? При повышении давления до 100 атм при 273 К?

Расставьте в порядке возрастания коэффициенты летучести азота при следующих условиях: 1 - 150 бар, 0 о. С 2 - 100 бар, -50 о. С 3 - 220 бар, -50 о. С 4 - 350 бар, 100 о. С 5 - 350 бар, 0 о. С

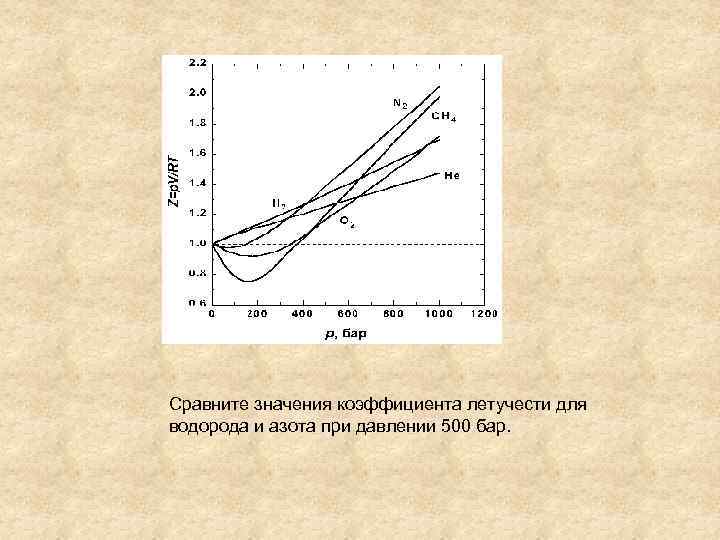Сравните значения коэффициента летучести для водорода и азота при давлении 500 бар.

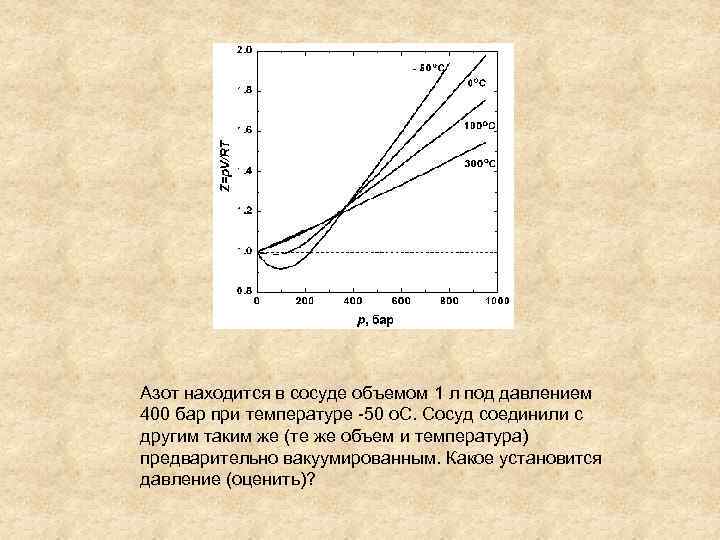Азот находится в сосуде объемом 1 л под давлением 400 бар при температуре -50 о. С. Сосуд соединили с другим таким же (те же объем и температура) предварительно вакуумированным. Какое установится давление (оценить)?

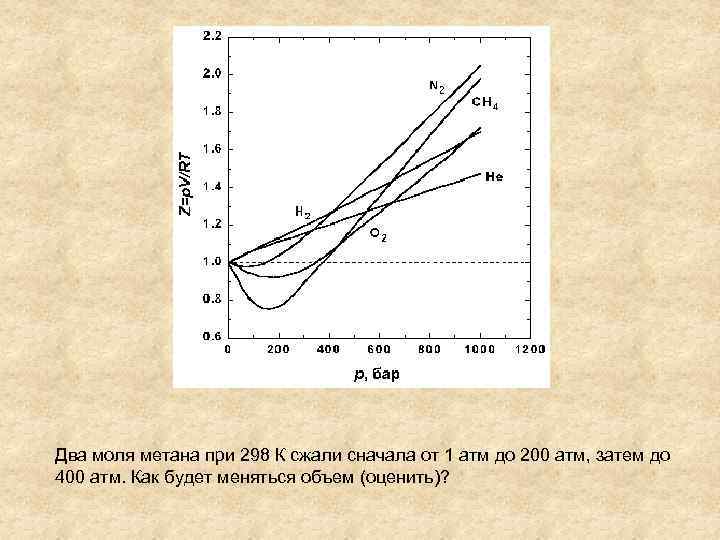Два моля метана при 298 К сжали сначала от 1 атм до 200 атм, затем до 400 атм. Как будет меняться объем (оценить)?