ФИЗИЧЕСКАЯ ОПТИКА для заочников.pptx
- Количество слайдов: 102
 ФИЗИЧЕСКАЯ ОПТИКА Для заочников
ФИЗИЧЕСКАЯ ОПТИКА Для заочников
 1. Волновое уравнение для электромагнитных волн и его решение.
1. Волновое уравнение для электромагнитных волн и его решение.
 • Процесс распространения колебаний в упругой среде называется волной • При распространении волны частицы не движутся вместе с волной, а колеблются около своих положений равновесия • Основное свойство волн – перенос энергии без переноса вещества
• Процесс распространения колебаний в упругой среде называется волной • При распространении волны частицы не движутся вместе с волной, а колеблются около своих положений равновесия • Основное свойство волн – перенос энергии без переноса вещества
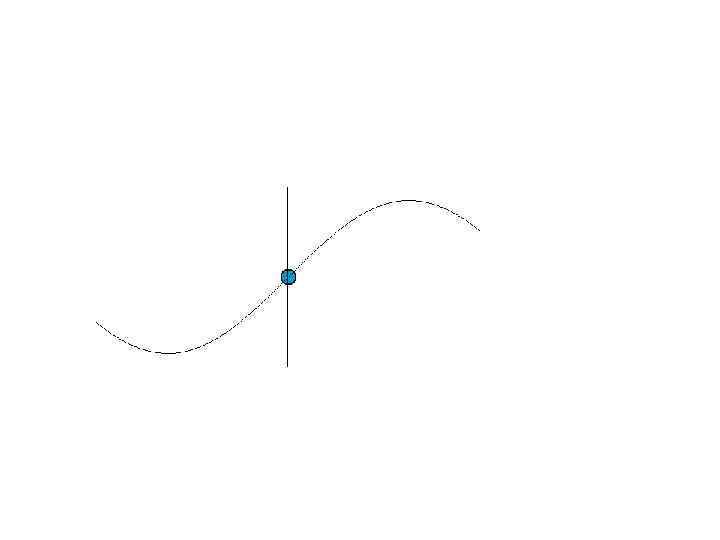
 • Продольные волны – частицы колеблются в направлении распространения волны
• Продольные волны – частицы колеблются в направлении распространения волны
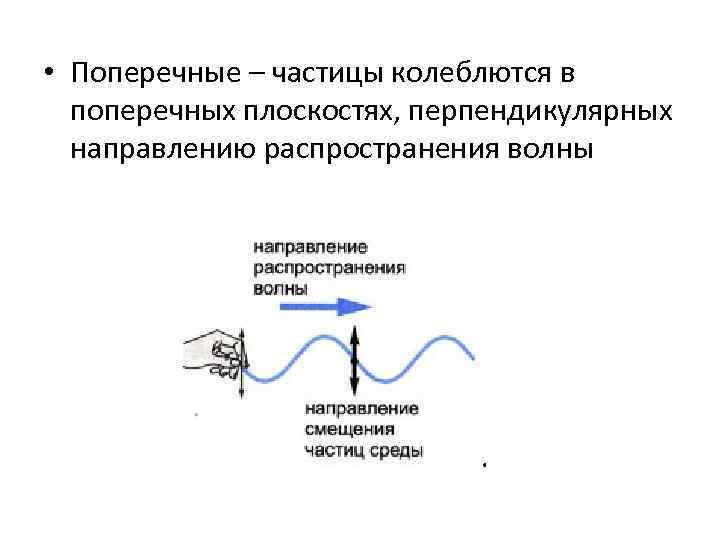 • Поперечные – частицы колеблются в поперечных плоскостях, перпендикулярных направлению распространения волны
• Поперечные – частицы колеблются в поперечных плоскостях, перпендикулярных направлению распространения волны
 • Геометрическое место точек, колеблющихся в одинаковой фазе, называют волновой поверхностью
• Геометрическое место точек, колеблющихся в одинаковой фазе, называют волновой поверхностью
 • Если волновая поверхность плоская, то волна называется плоской
• Если волновая поверхность плоская, то волна называется плоской
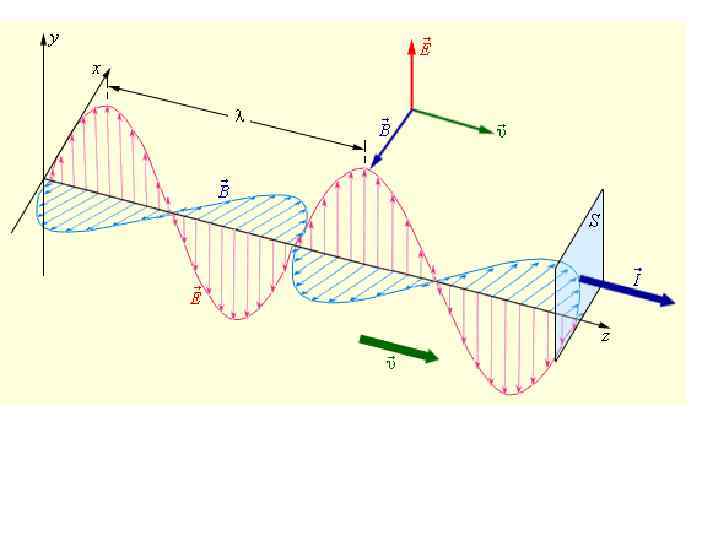
 • Электромагнитные волны поперечны – векторы E и B перпендикулярны другу и лежат в плоскости, перпендикулярной направлению распространения волны
• Электромагнитные волны поперечны – векторы E и B перпендикулярны другу и лежат в плоскости, перпендикулярной направлению распространения волны
 Волновое уравнение
Волновое уравнение
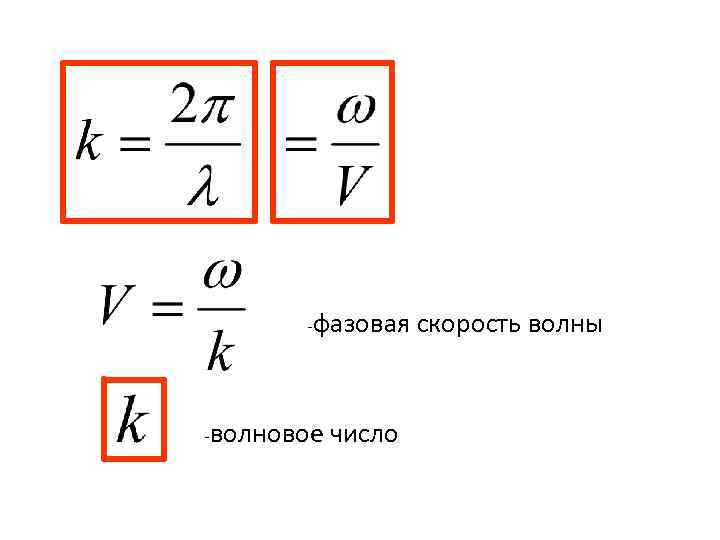 -фазовая -волновое число скорость волны
-фазовая -волновое число скорость волны
 2. Скорость света в среде • V - фазовая скорость
2. Скорость света в среде • V - фазовая скорость
 Оптическая длина пути
Оптическая длина пути
 3. ИНТЕРФЕРЕЦИЯ СВЕТОВЫХ ВОЛН
3. ИНТЕРФЕРЕЦИЯ СВЕТОВЫХ ВОЛН
 • ПРИ НАЛОЖЕНИИ ДВУХ И БОЛЕЕ КОГЕРЕНТНЫХ ВОЛН ПРОИСХОДИТ ПЕРЕРАСПРЕДЕЛЕНИЕ ИНТЕНСИВНОСТИ, ПРИ ЭТОМ НАБЛЮДАЮТСЯ МАКСИМУМЫ И МИНИМУМЫ ( СВЕТЛЫЕ И ТЕМНЫЕ ПОЛОСЫ) – ИНТЕРФЕРЕНЦИЯ СВЕТА
• ПРИ НАЛОЖЕНИИ ДВУХ И БОЛЕЕ КОГЕРЕНТНЫХ ВОЛН ПРОИСХОДИТ ПЕРЕРАСПРЕДЕЛЕНИЕ ИНТЕНСИВНОСТИ, ПРИ ЭТОМ НАБЛЮДАЮТСЯ МАКСИМУМЫ И МИНИМУМЫ ( СВЕТЛЫЕ И ТЕМНЫЕ ПОЛОСЫ) – ИНТЕРФЕРЕНЦИЯ СВЕТА
 • Когерентные волны – волны разность фаз которых не меняется с течением времени • Монохроматичекие волны – волны одной постоянной частоты
• Когерентные волны – волны разность фаз которых не меняется с течением времени • Монохроматичекие волны – волны одной постоянной частоты

 • Пусть интерференция наблюдается в некоторой точке, до которой первая волна прошла расстояние s 1 в среде с показателем преломления n 1, а вторая волна – s 2, n 2
• Пусть интерференция наблюдается в некоторой точке, до которой первая волна прошла расстояние s 1 в среде с показателем преломления n 1, а вторая волна – s 2, n 2
 • Первая волна возбудит колебания n Вторая волна
• Первая волна возбудит колебания n Вторая волна
 Разность фаз колебаний
Разность фаз колебаний
 - оптическая длина пути - разность хода
- оптическая длина пути - разность хода
 -условие максимума -( светлые полосы)
-условие максимума -( светлые полосы)
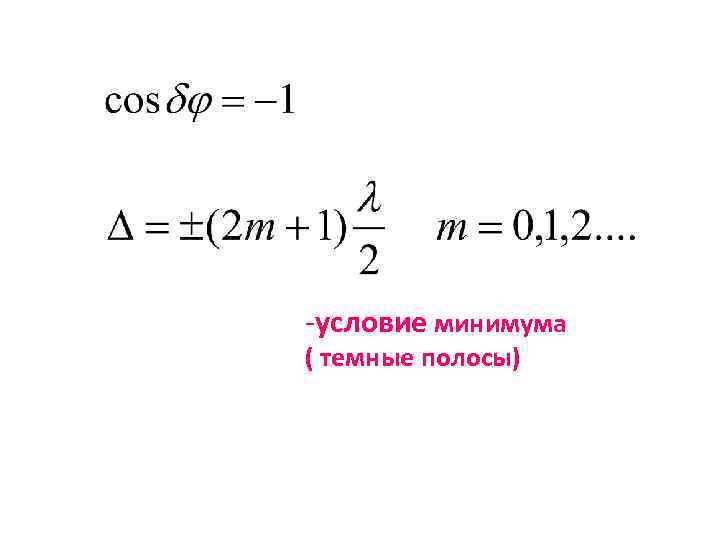 -условие минимума ( темные полосы)
-условие минимума ( темные полосы)
 4. РАСЧЕТ ИНТЕРФЕРЕНЦИОННОЙ КАРТИНЫ ОТ ДВУХ ИСТОЧНИКОВ
4. РАСЧЕТ ИНТЕРФЕРЕНЦИОННОЙ КАРТИНЫ ОТ ДВУХ ИСТОЧНИКОВ

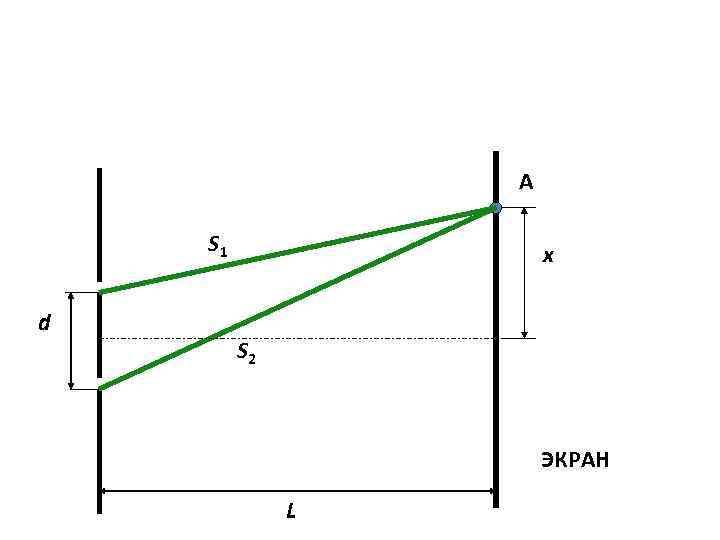 А S 1 d x S 2 ЭКРАН L
А S 1 d x S 2 ЭКРАН L
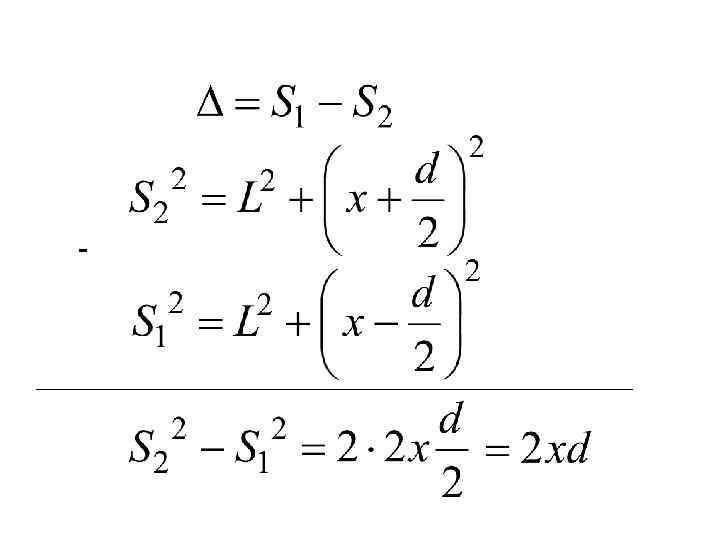 -
-
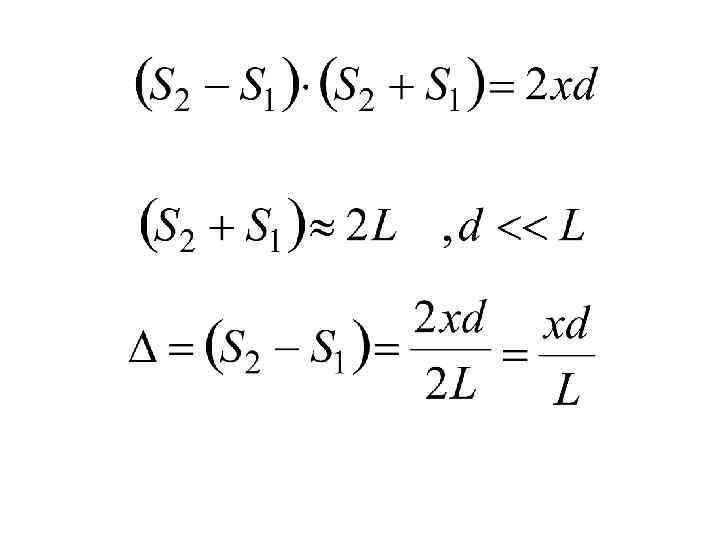
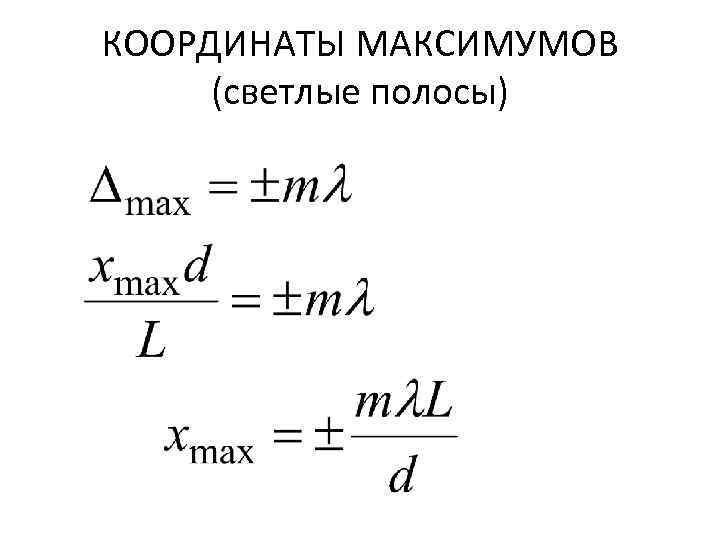 КООРДИНАТЫ МАКСИМУМОВ (светлые полосы)
КООРДИНАТЫ МАКСИМУМОВ (светлые полосы)
 КООРДИНАТЫ МИНИМУМОВ (темные полосы)
КООРДИНАТЫ МИНИМУМОВ (темные полосы)
 ИНТЕРФЕРЕНЦИЯ ПРИ ОТРАЖЕНИИ ОТ ТОНКИХ ПЛАСТИНОК
ИНТЕРФЕРЕНЦИЯ ПРИ ОТРАЖЕНИИ ОТ ТОНКИХ ПЛАСТИНОК

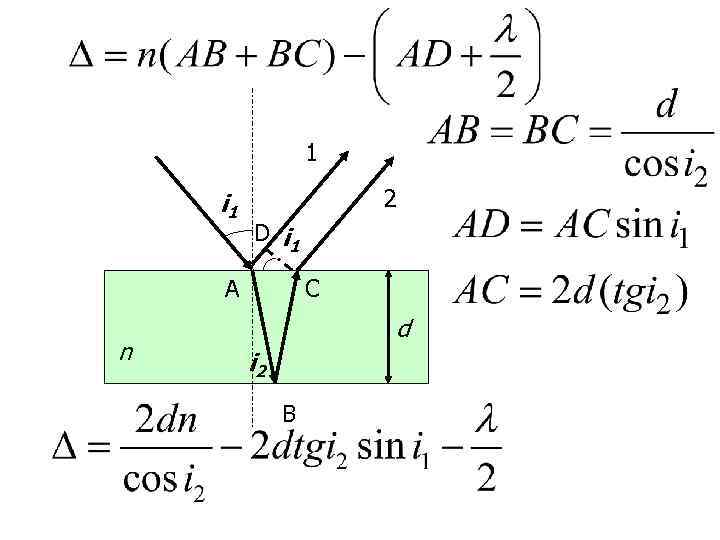 1 i 1 2 D i 1 А n С d i 2 В
1 i 1 2 D i 1 А n С d i 2 В
 • У отраженной от верхней поверхности волны фаза изменяется на π, что эквивалентно появлению дополнительной разности хода λ/2
• У отраженной от верхней поверхности волны фаза изменяется на π, что эквивалентно появлению дополнительной разности хода λ/2

 УСЛОВИЕ МАКСИМУМОВ
УСЛОВИЕ МАКСИМУМОВ
 УСЛОВИЕ МИНИМУМОВ
УСЛОВИЕ МИНИМУМОВ
 6. ДИФРАКЦИЯ СВЕТА
6. ДИФРАКЦИЯ СВЕТА
 Дифракция – огибание волной препятствия
Дифракция – огибание волной препятствия
 ПРИНЦИП ГЮЙГЕНСА • Любая точка, до которой доходит волна, служит источником вторичных волн, а огибающая этих волн дает положение волнового фронта в следующий момент времени
ПРИНЦИП ГЮЙГЕНСА • Любая точка, до которой доходит волна, служит источником вторичных волн, а огибающая этих волн дает положение волнового фронта в следующий момент времени
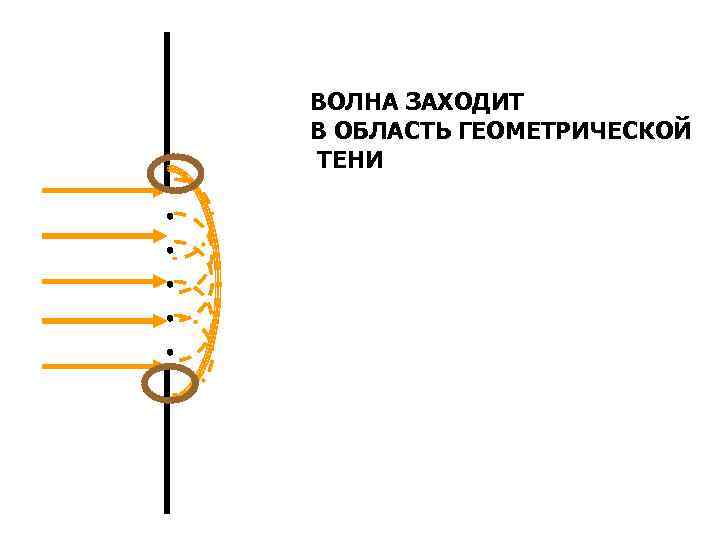 ВОЛНА ЗАХОДИТ В ОБЛАСТЬ ГЕОМЕТРИЧЕСКОЙ ТЕНИ
ВОЛНА ЗАХОДИТ В ОБЛАСТЬ ГЕОМЕТРИЧЕСКОЙ ТЕНИ
 • ПРИНЦИП ГЮЙГЕНСА • указывает лишь направление распространения волны • не рассматривает интенсивности распространяющихся волн • не может объяснить прямолинейное распространение света
• ПРИНЦИП ГЮЙГЕНСА • указывает лишь направление распространения волны • не рассматривает интенсивности распространяющихся волн • не может объяснить прямолинейное распространение света
 ПРИНЦИП ГЮЙГЕНСА ФРЕНЕЛЯ
ПРИНЦИП ГЮЙГЕНСА ФРЕНЕЛЯ
 • Световая волна, возбуждаемая каким-либо источником, может быть представлена как результат суперпозиции когерентных вторичных волн
• Световая волна, возбуждаемая каким-либо источником, может быть представлена как результат суперпозиции когерентных вторичных волн
 МЕТОД ЗОН ФРЕНЕЛЯ
МЕТОД ЗОН ФРЕНЕЛЯ
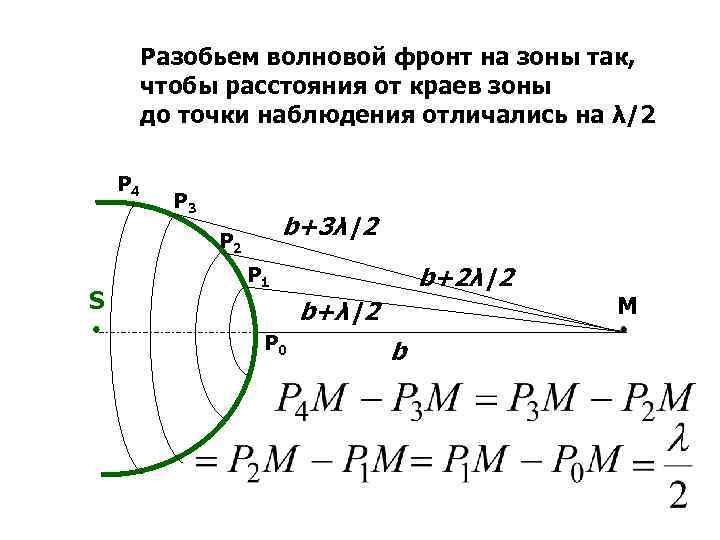 Разобьем волновой фронт на зоны так, чтобы расстояния от краев зоны до точки наблюдения отличались на λ/2 Р 4 Р 3 b+3λ|2 Р 2 S b+2λ|2 Р 1 b+λ|2 Р 0 b M
Разобьем волновой фронт на зоны так, чтобы расстояния от краев зоны до точки наблюдения отличались на λ/2 Р 4 Р 3 b+3λ|2 Р 2 S b+2λ|2 Р 1 b+λ|2 Р 0 b M
 радиус внешней границы m зоны Френеля
радиус внешней границы m зоны Френеля
 • a – расстояние от источника до волновой поверхности • b - расстояние от волновой поверхности до точки наблюдения
• a – расстояние от источника до волновой поверхности • b - расстояние от волновой поверхности до точки наблюдения
 • Если источник света находится на бесконечности (плоская волна)
• Если источник света находится на бесконечности (плоская волна)
 7. ДИФРАКЦИЯ ФРАУНГОФЕРА НА ОДНОЙ ЩЕЛИ
7. ДИФРАКЦИЯ ФРАУНГОФЕРА НА ОДНОЙ ЩЕЛИ
 • Дифракция Фраунгофера – дифракция плоских волн (источник расположен на бесконечности)
• Дифракция Фраунгофера – дифракция плоских волн (источник расположен на бесконечности)
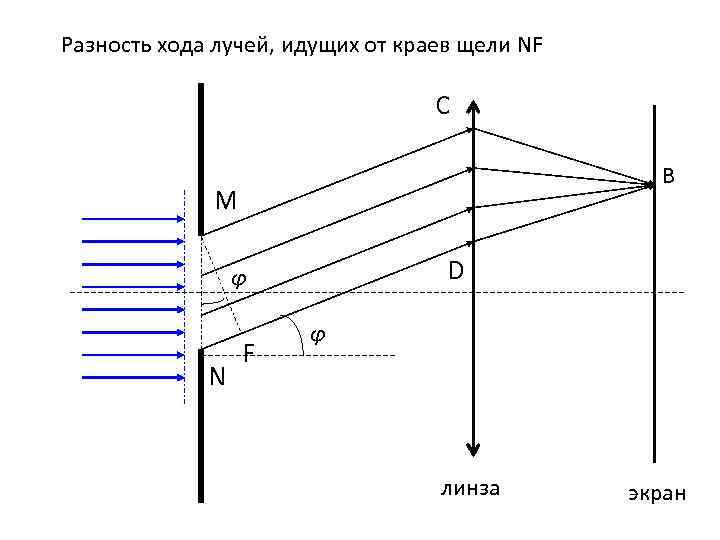 Разность хода лучей, идущих от краев щели NF C В M D φ N F φ линза экран
Разность хода лучей, идущих от краев щели NF C В M D φ N F φ линза экран
 • Разобьем мысленно щель на зоны Френеля , имеющие вид полос • Разность хода от краев зоны λ/2 • Амплитуды вторичных волн будут равны между собой • При интерференции волн от соседних зон они гасят друга
• Разобьем мысленно щель на зоны Френеля , имеющие вид полос • Разность хода от краев зоны λ/2 • Амплитуды вторичных волн будут равны между собой • При интерференции волн от соседних зон они гасят друга
 Если число зон Френеля четное – наблюдается дифракционный минимум, так как волны от соседних зон гасят друга
Если число зон Френеля четное – наблюдается дифракционный минимум, так как волны от соседних зон гасят друга
 Если число зон Френеля нечетное – наблюдается дифракционный максимум
Если число зон Френеля нечетное – наблюдается дифракционный максимум
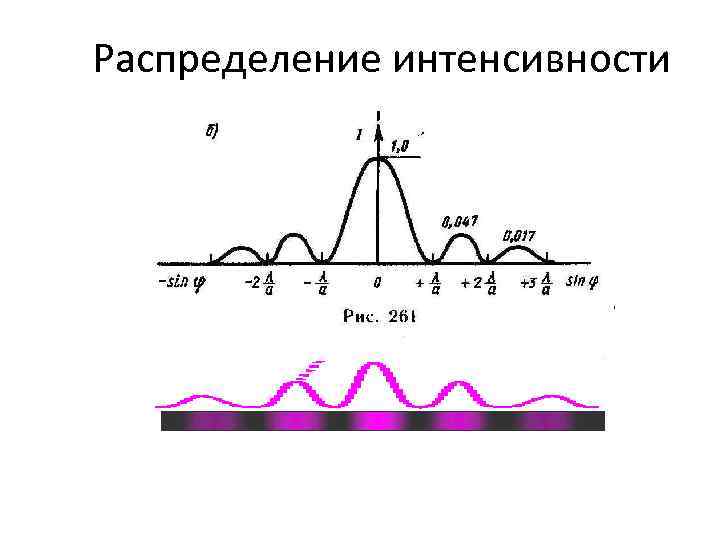 Распределение интенсивности
Распределение интенсивности
 ДИФРАКЦИЯ ФРАУНГОФЕРА НА ДИФРАКЦИОННОЙ РЕШЕТКЕ
ДИФРАКЦИЯ ФРАУНГОФЕРА НА ДИФРАКЦИОННОЙ РЕШЕТКЕ
 • Дифракционная решетка – система параллельных щелей равной ширины, разделенных между собой непрозрачными промежутками
• Дифракционная решетка – система параллельных щелей равной ширины, разделенных между собой непрозрачными промежутками
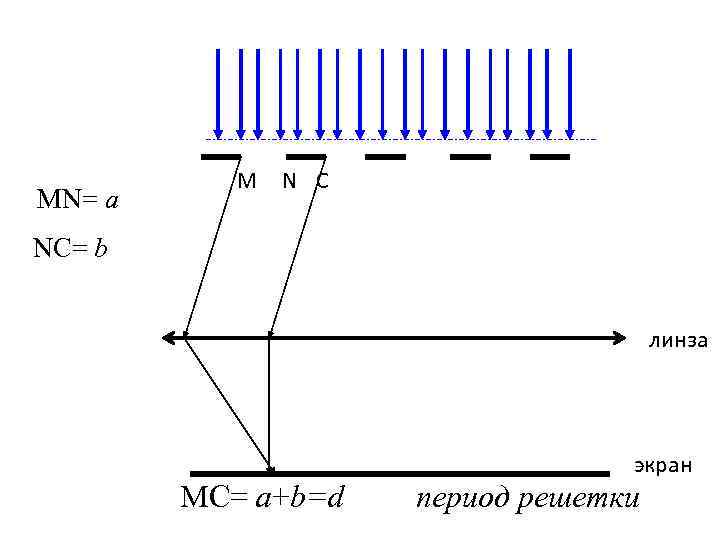 MN= a M N C NC= b линза MC= a+b=d экран период решетки
MN= a M N C NC= b линза MC= a+b=d экран период решетки
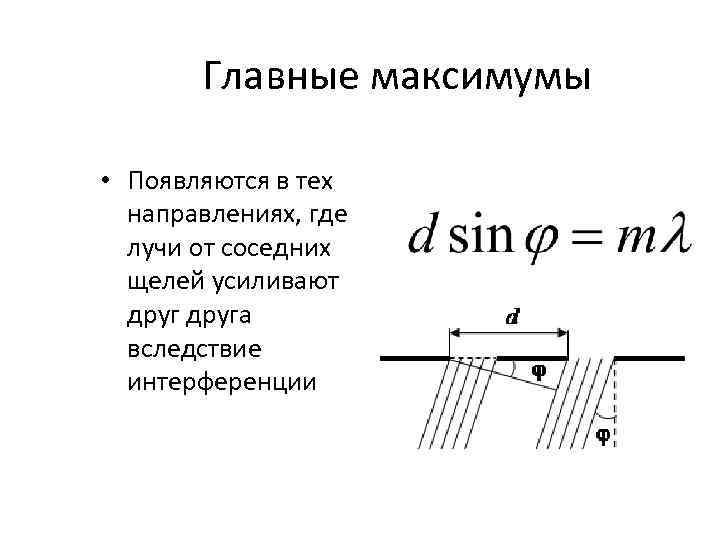 Главные максимумы • Появляются в тех направлениях, где лучи от соседних щелей усиливают друга вследствие интерференции
Главные максимумы • Появляются в тех направлениях, где лучи от соседних щелей усиливают друга вследствие интерференции
 • При наблюдается центральный максимум n n По обе стороны от центрального максимума располагаются главные максимумы 1 порядка, 2 порядка и т. д. Количество главных максимумов ограничено
• При наблюдается центральный максимум n n По обе стороны от центрального максимума располагаются главные максимумы 1 порядка, 2 порядка и т. д. Количество главных максимумов ограничено
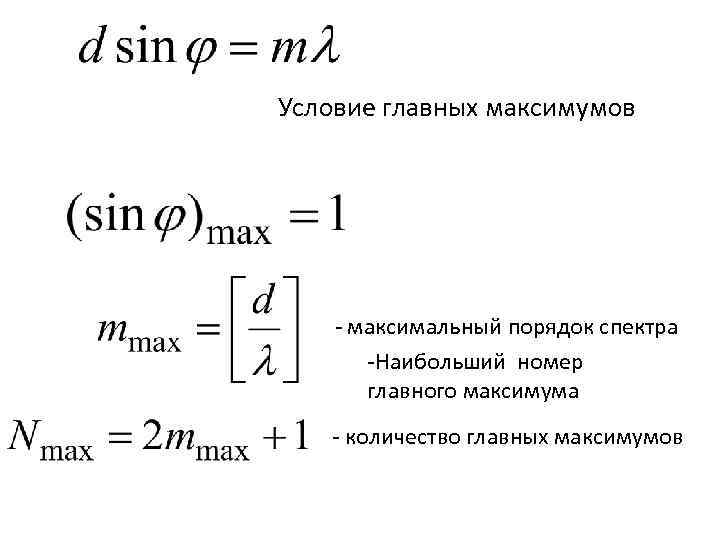 Условие главных максимумов - максимальный порядок спектра -Наибольший номер главного максимума - количество главных максимумов
Условие главных максимумов - максимальный порядок спектра -Наибольший номер главного максимума - количество главных максимумов
 • В тех направлениях, где одна щель дает минимум , то и другая щель также дает минимум • Эти минимумы называются главными
• В тех направлениях, где одна щель дает минимум , то и другая щель также дает минимум • Эти минимумы называются главными
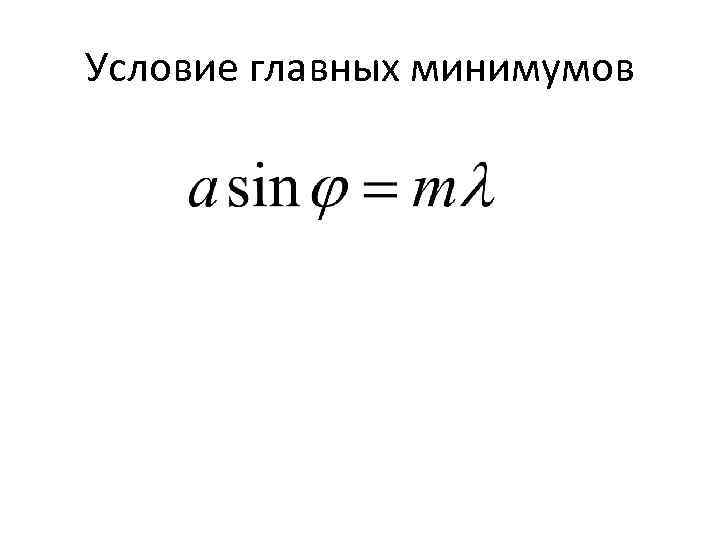 Условие главных минимумов
Условие главных минимумов
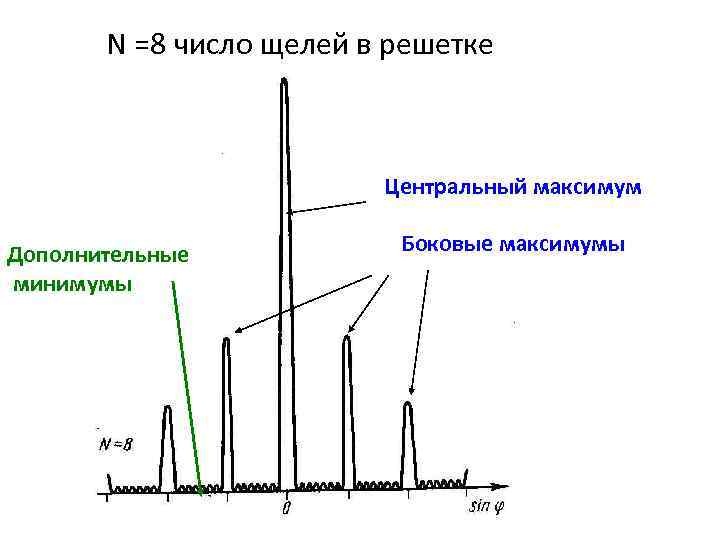 N =8 число щелей в решетке Центральный максимум Дополнительные минимумы Боковые максимумы
N =8 число щелей в решетке Центральный максимум Дополнительные минимумы Боковые максимумы
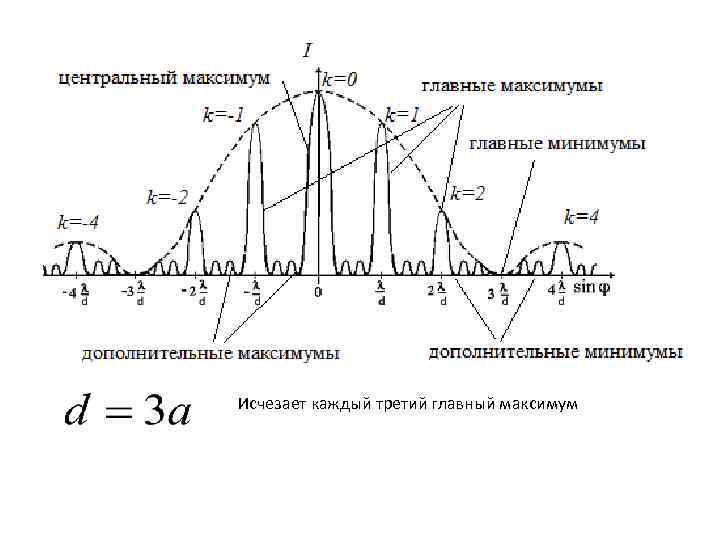 Исчезает каждый третий главный максимум
Исчезает каждый третий главный максимум
 Дифракция белого света на дифракционной решетке • Появляются в тех направлениях, где лучи от соседних щелей гасят друга вследствие интерференции • Между двумя главными максимумами располагается (N-1) дополнительный минимум
Дифракция белого света на дифракционной решетке • Появляются в тех направлениях, где лучи от соседних щелей гасят друга вследствие интерференции • Между двумя главными максимумами располагается (N-1) дополнительный минимум
 9. ПОЛЯРИЗАЦИЯ
9. ПОЛЯРИЗАЦИЯ
 - световой вектор • Волна, в которой колебания светового вектора какимлибо образом упорядочены, называется ПОЛЯРИЗОВАННОЙ. • Если световой вектор колеблется в одной плоскости, то волна называется ПЛОСКО- (ЛИНЕЙНО) ПОЛЯРИЗОВАННОЙ • Если световой вектор вращается вокруг направления распространения волны, причем его конец описывает эллипс, то волна называется ЭЛЛИПТИЧЕСКИПОЛЯРИЗОВАННОЙ
- световой вектор • Волна, в которой колебания светового вектора какимлибо образом упорядочены, называется ПОЛЯРИЗОВАННОЙ. • Если световой вектор колеблется в одной плоскости, то волна называется ПЛОСКО- (ЛИНЕЙНО) ПОЛЯРИЗОВАННОЙ • Если световой вектор вращается вокруг направления распространения волны, причем его конец описывает эллипс, то волна называется ЭЛЛИПТИЧЕСКИПОЛЯРИЗОВАННОЙ
 • Свет, испускаемый обычными источниками (солнечный свет, излучение ламп накаливания ), неполяризован. • Неполяризованный свет называют также естественным светом.
• Свет, испускаемый обычными источниками (солнечный свет, излучение ламп накаливания ), неполяризован. • Неполяризованный свет называют также естественным светом.
 ПОЛЯРИЗАТОРЫ • ПОЛЯРИЗАТОР – прибор для превращения естественного света в поляризованный • Поляризатор пропускает колебания параллельные ПЛОСКОСТИ ПРОПУСКАНИЯ ПОЛЯРИЗАТОРА
ПОЛЯРИЗАТОРЫ • ПОЛЯРИЗАТОР – прибор для превращения естественного света в поляризованный • Поляризатор пропускает колебания параллельные ПЛОСКОСТИ ПРОПУСКАНИЯ ПОЛЯРИЗАТОРА
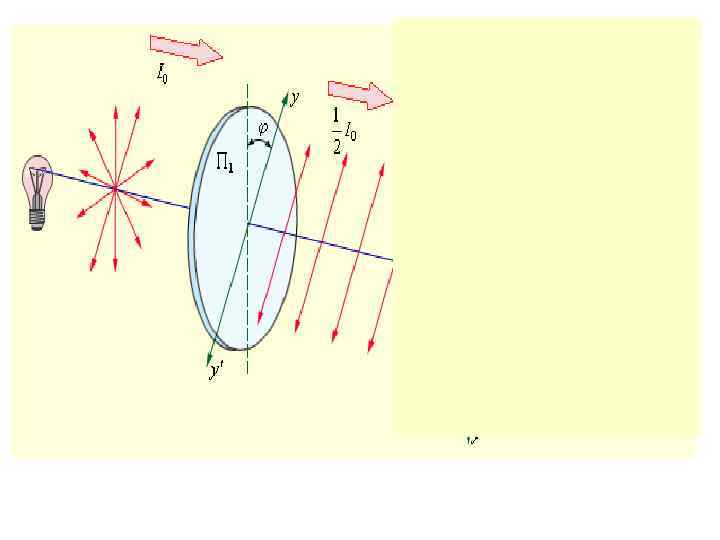
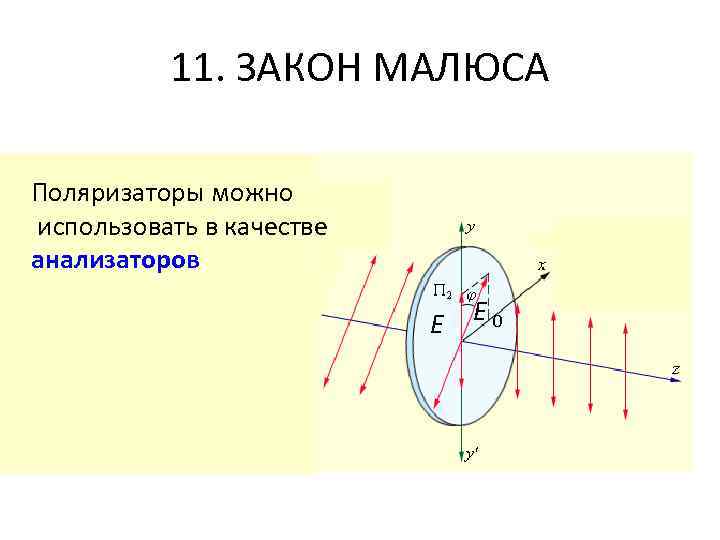 11. ЗАКОН МАЛЮСА Поляризаторы можно использовать в качестве анализаторов Е Е 0
11. ЗАКОН МАЛЮСА Поляризаторы можно использовать в качестве анализаторов Е Е 0
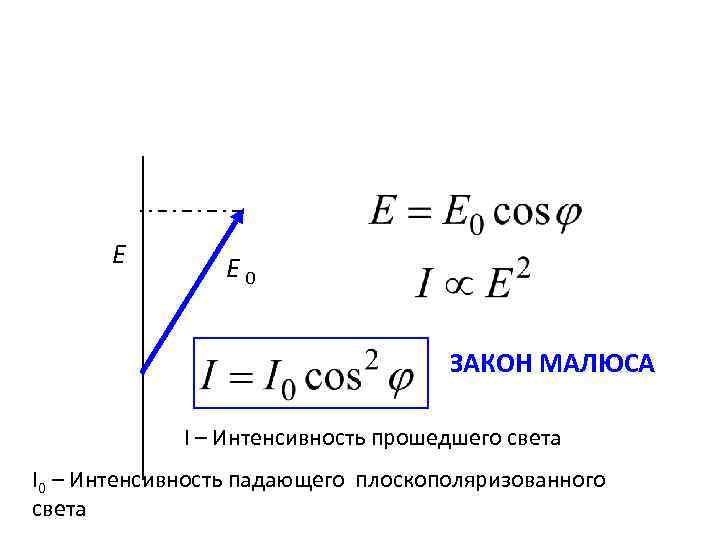 Е Е 0 ЗАКОН МАЛЮСА I – Интенсивность прошедшего света I 0 – Интенсивность падающего плоскополяризованного света
Е Е 0 ЗАКОН МАЛЮСА I – Интенсивность прошедшего света I 0 – Интенсивность падающего плоскополяризованного света
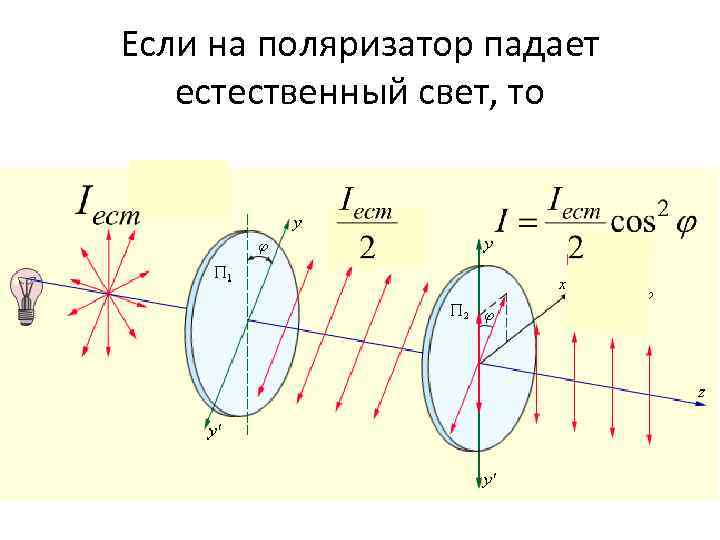 Если на поляризатор падает естественный свет, то
Если на поляризатор падает естественный свет, то
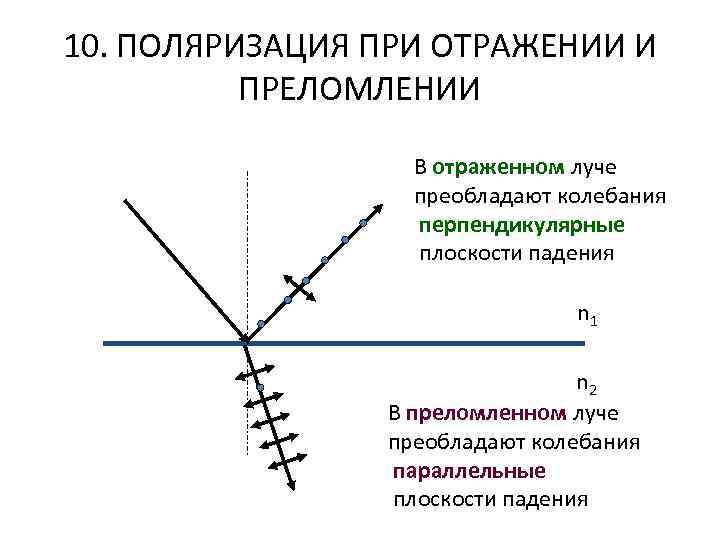 10. ПОЛЯРИЗАЦИЯ ПРИ ОТРАЖЕНИИ И ПРЕЛОМЛЕНИИ В отраженном луче преобладают колебания перпендикулярные плоскости падения n 1 n 2 В преломленном луче преобладают колебания параллельные плоскости падения
10. ПОЛЯРИЗАЦИЯ ПРИ ОТРАЖЕНИИ И ПРЕЛОМЛЕНИИ В отраженном луче преобладают колебания перпендикулярные плоскости падения n 1 n 2 В преломленном луче преобладают колебания параллельные плоскости падения
 УГОЛ БРЮСТЕРА • При некотором угле падения отраженный свет полностью поляризован • Этот угол называется углом Брюстера
УГОЛ БРЮСТЕРА • При некотором угле падения отраженный свет полностью поляризован • Этот угол называется углом Брюстера
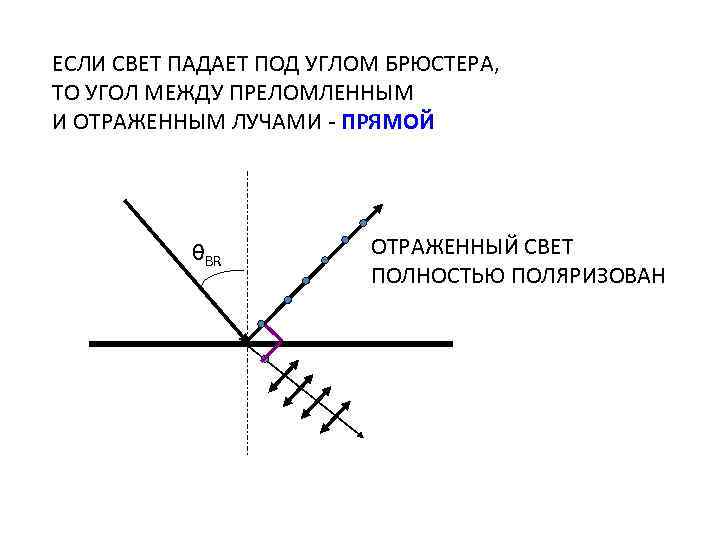 ЕСЛИ СВЕТ ПАДАЕТ ПОД УГЛОМ БРЮСТЕРА, ТО УГОЛ МЕЖДУ ПРЕЛОМЛЕННЫМ И ОТРАЖЕННЫМ ЛУЧАМИ - ПРЯМОЙ θBR ОТРАЖЕННЫЙ СВЕТ ПОЛНОСТЬЮ ПОЛЯРИЗОВАН
ЕСЛИ СВЕТ ПАДАЕТ ПОД УГЛОМ БРЮСТЕРА, ТО УГОЛ МЕЖДУ ПРЕЛОМЛЕННЫМ И ОТРАЖЕННЫМ ЛУЧАМИ - ПРЯМОЙ θBR ОТРАЖЕННЫЙ СВЕТ ПОЛНОСТЬЮ ПОЛЯРИЗОВАН
 12. ТЕПЛОВОЕ ИЗЛУЧЕНИЕ И ЕГО ХАРАКТЕРИСТИКИ
12. ТЕПЛОВОЕ ИЗЛУЧЕНИЕ И ЕГО ХАРАКТЕРИСТИКИ
 • Свечение тел, обусловленное нагреванием называется ТЕПЛОВЫМ ИЗЛУЧЕНИЕМ • Совершается за счет энергии теплового движения атомов и молекул • Характеризуется сплошным спектром • При высоких температурах излучаются короткие волны • При низких температурах - длинные
• Свечение тел, обусловленное нагреванием называется ТЕПЛОВЫМ ИЗЛУЧЕНИЕМ • Совершается за счет энергии теплового движения атомов и молекул • Характеризуется сплошным спектром • При высоких температурах излучаются короткие волны • При низких температурах - длинные
 • ТЕПЛОВОЕ ИЗЛУЧЕНИЕ - РАВНОВЕСНОЕ ИЗЛУЧЕНИЕ • ( т. е сколько энергии в ед. времени излучается столько же и поглощается)
• ТЕПЛОВОЕ ИЗЛУЧЕНИЕ - РАВНОВЕСНОЕ ИЗЛУЧЕНИЕ • ( т. е сколько энергии в ед. времени излучается столько же и поглощается)
 Абсолютно черное тело • При любой температуре полностью поглощает падающее излучение в любом диапазоне частот
Абсолютно черное тело • При любой температуре полностью поглощает падающее излучение в любом диапазоне частот
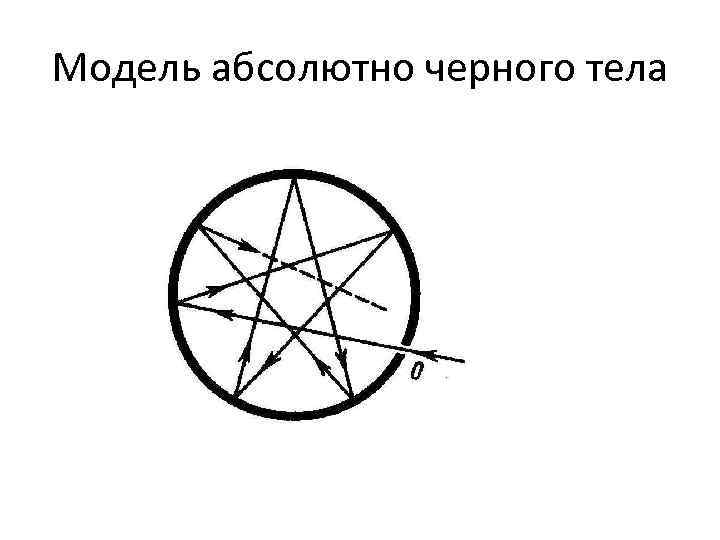 Модель абсолютно черного тела
Модель абсолютно черного тела
 Серое тело • Поглощательная способность меньше 1, но одинакова для всех частот и зависит только от температуры
Серое тело • Поглощательная способность меньше 1, но одинакова для всех частот и зависит только от температуры
 Закон Стефана-Больцмана • Энергетическая светимость черного тела пропорциональна четвертой степени температуры Вт/м 2 К 4
Закон Стефана-Больцмана • Энергетическая светимость черного тела пропорциональна четвертой степени температуры Вт/м 2 К 4
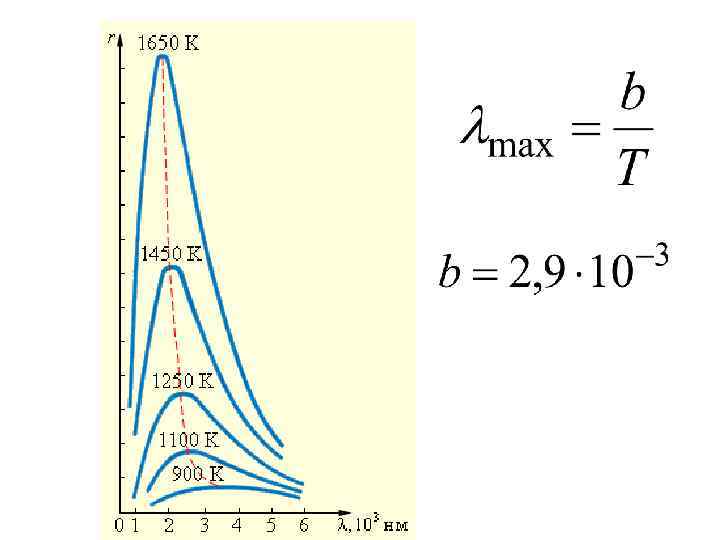
 Закон смещения Вина
Закон смещения Вина
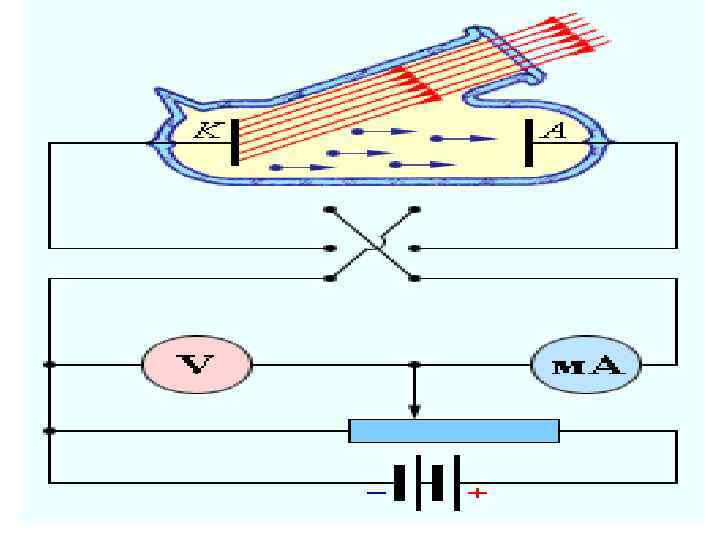
 13. ФОТОЭФФЕКТ • Внешний фотоэффект – вырывание электронов вещества под действием электромагнитного излучения
13. ФОТОЭФФЕКТ • Внешний фотоэффект – вырывание электронов вещества под действием электромагнитного излучения
 • ФОТОЭФФЕКТ НЕВОЗМОЖНО ОБЪЯСНИТЬ С КЛАССИЧЕСКОЙ ТОЧКИ ЗРЕНИЯ
• ФОТОЭФФЕКТ НЕВОЗМОЖНО ОБЪЯСНИТЬ С КЛАССИЧЕСКОЙ ТОЧКИ ЗРЕНИЯ
 УРАВНЕНИЕ ЭЙНШТЕЙНА • Свет не только испускается, но распространяется и поглощается отдельными порциями – КВАНТАМИ • Кванты электромагнитного излучения наз. ФОТОНАМИ • Энергия одного кванта
УРАВНЕНИЕ ЭЙНШТЕЙНА • Свет не только испускается, но распространяется и поглощается отдельными порциями – КВАНТАМИ • Кванты электромагнитного излучения наз. ФОТОНАМИ • Энергия одного кванта
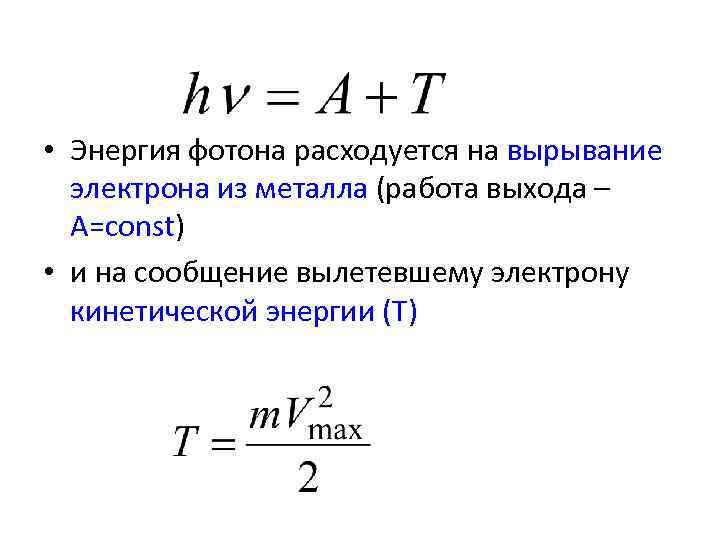 • Энергия фотона расходуется на вырывание электрона из металла (работа выхода – A=const) • и на сообщение вылетевшему электрону кинетической энергии (Т)
• Энергия фотона расходуется на вырывание электрона из металла (работа выхода – A=const) • и на сообщение вылетевшему электрону кинетической энергии (Т)
 CУЩЕСТВУЕТ КРАСНАЯ ГРАНИЦА ФОТОЭФФЕКТА, Т. е. МИНИМАЛЬНАЯ ЧАСТОТА ПАДАЮЩЕГО СВЕТА , ПРИ КОТОРОЙ ЕЩЕ ВОЗМОЖЕН ФОТОЭФФЕКТ
CУЩЕСТВУЕТ КРАСНАЯ ГРАНИЦА ФОТОЭФФЕКТА, Т. е. МИНИМАЛЬНАЯ ЧАСТОТА ПАДАЮЩЕГО СВЕТА , ПРИ КОТОРОЙ ЕЩЕ ВОЗМОЖЕН ФОТОЭФФЕКТ
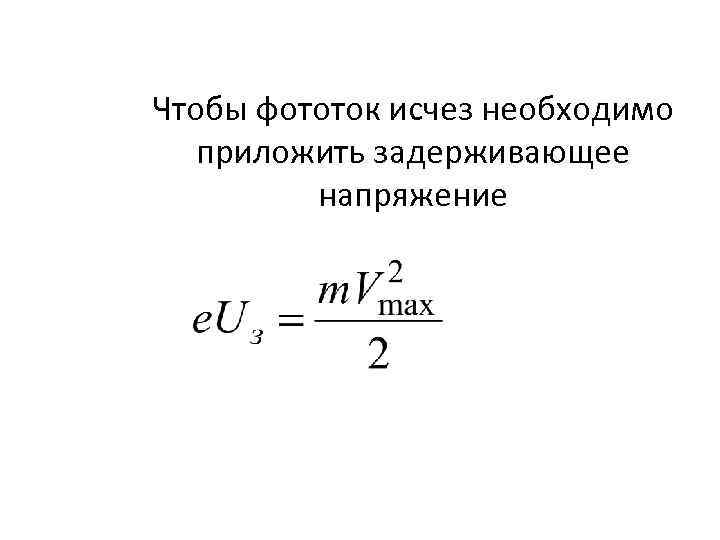 Чтобы фототок исчез необходимо приложить задерживающее напряжение
Чтобы фототок исчез необходимо приложить задерживающее напряжение
 14. ЭФФЕКТ КОМПТОНА
14. ЭФФЕКТ КОМПТОНА
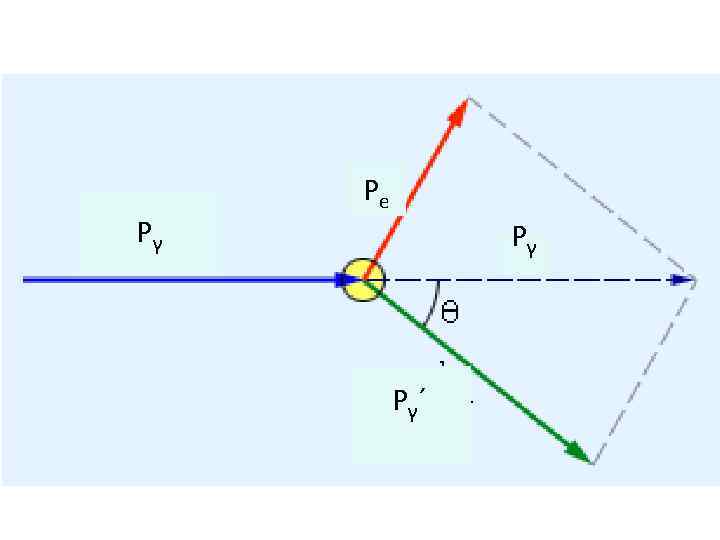
 • Упругое рассеяние коротковолнового рентгеновского излучения на свободных (или слабо связанных с атомами) электронах вещества. • При этом наблюдается увеличение длины волны рассеянного излучения в зависимости от угла рассеяния
• Упругое рассеяние коротковолнового рентгеновского излучения на свободных (или слабо связанных с атомами) электронах вещества. • При этом наблюдается увеличение длины волны рассеянного излучения в зависимости от угла рассеяния
 Pγ Pe Pγ P γ´
Pγ Pe Pγ P γ´
 • Pe – Импульс электрона после столкновения • Pγ ´– Импульс фотона после столкновения • Pγ – Импульс фотона до столкновения
• Pe – Импульс электрона после столкновения • Pγ ´– Импульс фотона после столкновения • Pγ – Импульс фотона до столкновения
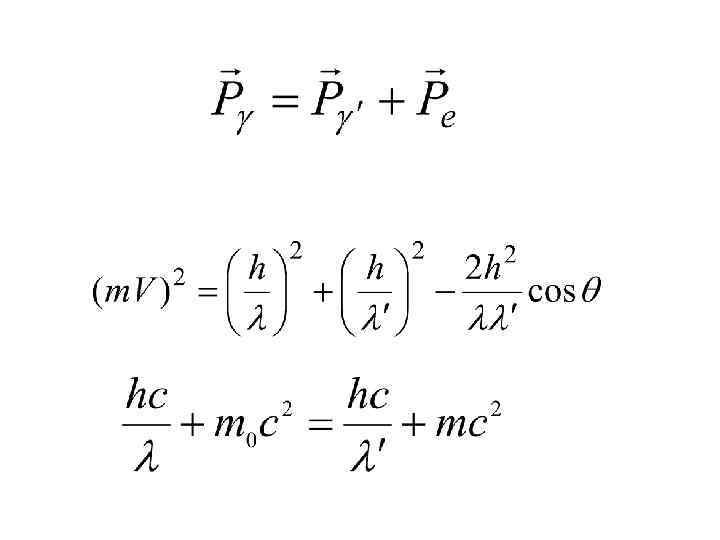
 Закон сохранения энергии - Энергия падающего фотона - Энергия рассеянного фотона - Энергия покоящегося электрона - Энергия электрона отдачи
Закон сохранения энергии - Энергия падающего фотона - Энергия рассеянного фотона - Энергия покоящегося электрона - Энергия электрона отдачи
 Изменение длины волны Θ – угол рассеяния пм – комптоновская длина волны
Изменение длины волны Θ – угол рассеяния пм – комптоновская длина волны


