физхимия.ppt
- Количество слайдов: 73

ФИЗИЧЕСКАЯ И КОЛЛОИДНАЯ ХИМИЯ Крисюк Борис Эдуардович

Рекомендованная литература. l l l К. И. Евстратова, Н. И. Купина, Е. Е. Малахова, Физическая и коллоидная химия, М. , Высшая школа, 1990, 487 с. В. В. Белик, К. И. Киенская, Физическая и коллоидная химия, М. , Академия, 2006, 288 с. С. И. Левченков, Физическая и коллоидная химия, лекции, http: //www. physchem. chimfak. rsu. ru/Source/PCC/i ndex. html

Основы химической термодинамики. l Системой будем называть тело или группу тел, отделенных от окружающей среды реальной или мысленной границей. Система называется термодинамической если между ее элементами происходит обмен энергией, веществом. l Окружающая среда – это все то, что находится в контакте с системой. l Открытая система может обмениваться с окружающей средой и энергией, и веществом, закрытая – только энергией, а изолированная не обменивается ничем. l Фаза – это часть системы, отделенная от нее поверхностью раздела фаз и характеризующаяся одинаковыми физическими свойствами во всех ее точках. Если система состоит из одной фазы, она называется гомогенной. Гетерогенная система состоит из нескольких фаз.

l Совокупность всех физических и химических свойств системы характеризует ее термодинамическое состояние. l Состояние системы характеризуют термодинамическими параметрам, которые можно экспериментально измерить. l Параметры, значения которых не зависят от массы (температура, давление, плотность, концентрация и др. ), называются интенсивными. l экстенсивные параметры зависят от массы (объем, масса, внутренняя энергия, теплоемкость и др. ).

Основные термодинамические функции состояний. Внутренняя энергия и энтальпия. l Внутренняя энергия (U) характеризует общий запас энергии системы. U = U 2 – U 1 l Энтальпия (H) это энергия системы при постоянном давлении, она равна сумме внутренней энергии и потенциальной энергии системы в целом: H = U + p. V

Теплота и работа. l Передача энергии от одной системы к другой осуществляется в виде теплоты (Q) и работы (A). Теплотой называют передачу энергии от системы к системе в виде неупорядоченного хаотического движения атомов и молекул. В противоположность этому работа – передача энергии путем упорядоченного движения элементов системы (например, газ двигает поршень). l Теплота и работа характеризуют не энергию, а лишь формы ее передачи, поэтому они зависят от пути процесса и не являются функциями состояния.

Нулевой закон термодинамики. l Нулевой закон термодинамики гласит, что если каждая из систем А и B находятся в равновесии с системой C, то они находятся и в равновесии друг с другом:

Первый закон термодинамики l Первый закон (начало) термодинамики является следствием закона сохранения энергии и имеет несколько формулировок: l - энергия изолированной системы постоянна - вечный двигатель первого рода (работающий без затрат энергии) невозможен - энергия не исчезает и не возникает из ничего, переход ее из одного вида в другой происходит в строго эквивалентных количествах l l l Первое начало термодинамики является постулатом

– Из последнего определения следует: l – Q = U + A то есть, подводимое к системе тепло идет на изменение ее внутренней энергии и на совершение ею работы. Таким образом, если реакция протекает при постоянном объеме Q = U, а при постоянном давлении Q = Н.

Законы термохимии l l Стандартная теплота образования вещества( Н 0 f ) – это тепловой эффект реакции образования 1 моля данного вещества из простых веществ или элементов в стандартных условиях (Р = 105 Па и Т = 298 К). Стандартной теплотой сгорания ( Н 0 с) называют тепловой эффект реакции сжигания 1 моля вещества до простейших оксидов в атмосфере кислорода и при стандартных условиях.

Закон Гесса l l l Тепловой эффект реакции – это количество теплоты, выделившееся или поглотившееся в ходе реакции. закон Гесса: Тепловой эффект реакции не зависит от пути процесса и определяется только конечным и начальным состоянием.

Следствия из закона Гесса. – – 1. Тепловой эффект прямой реакции равен по величине и противоположен по знаку тепловому эффекту обратной реакции (закон Лавуазье Лапласа). 2. Для двух реакций, имеющих одинаковые исходные, но разные конечные состояния, разность тепловых эффектов есть тепловой эффект перехода из одного конечного состояния в другое. Пример: l l С + О 2 → СО + ½О 2 С + О 2 → СО 2 СО + ½О 2 → СО 2 Тогда: Н 3 = Н 2 – Н 1. ( Н 1) ( Н 2) ( Н 3)

Следствия из закона Гесса. l l 3. Для двух реакций, имеющих разное исходное, но одинаковое конечное состояние, разность тепловых эффектов равна теплоте перехода из одного исходного состояния в другое. Пример: l Салмаз + О 2 → СО 2 ( Н 1) l Сграфит + О 2 → СО 2 ( Н 2) l Салмаз → Сграфит ( Н 3) Тогда: Н 3 = Н 1 – Н 2. 4. Тепловой эффект реакции при стандартных условиях равен разности между суммами стандартных теплот образования продуктов и реагентов, умноженных на соответствующие стехиометрические коэффициенты i: l Н 0 = i Н 0 f, прод i Н 0 f, реаг 5. Тепловой эффект реакции при стандартных условиях равен разности между суммами стандартных теплот сгорания реагентов и продуктов, умноженных на соответствующие стехиометрические коэффициенты i: l Н 0 = i Н 0 с, реаг. i Н 0 с, прод

Задачи на закон Гесса – Задача 1. Рассчитать тепловой эффект реакции (все реагенты – газ): l CH 4 + CO 2 = 2 CO + 2 H 2 – Стандартные теплоты образования: Н 0 f, 1 = 74, 85 к. Дж/моль; Н 0 f, 2 = 393, 51; Н 0 f, 3 = 110, 5; Н 0 f, 4 = 0 (простое вещество). – Решение: Н 0 = i Н 0 f, прод i Н 0 f, реаг = 2( 110, 5 + 0) – ( 74, 85 – 393, 51) = +247, 4 Ответ: +247, 4 к. Дж/моль – эндотермический процесс. – –

Второе начало термодинамики. Энтропия. l l l Понятие об энтропии ввел Клаузиус, рассматривая цикл Карно, для к. п. д. которого можно записать выражение: – = (Q 1 – Q 2)/Q 1 = (T 1 – T 2)/T 1 где Q 1 теплота, полученная системой от нагревателя температурой Т 1 , а Q 2 – теплота, отданная нагревателю при температуре системы Т 2. Из этого равенства: Q 1 / T 1 + Q 2 / T 2 = 0 для замкнутого цикла. Но любой произвольный цикл можно представить как сумму бесконечно малых циклов Карно. Это означает, что для произвольного цикла Q/ T = 0, и существует функция состояния S, для которой: l d. S = Q/ T

l Это выражение второго закона термодинамики для произвольного обратимого процесса. Для необратимого процесса знак равенства l заменяется на неравенство и в общем случае: l d. S ≥ Q/ T Это означает, что любая форма энергии может полностью перейти в теплоту, тогда как теплота может преобразоваться в энергию лишь частично. Иначе говоря, внутреннюю энергию системы можно представить себе как сумму «свободной» и «связанной» энергий, причем свободная может быть затрачена на работу, а связанная может преобразовываться только в тепло. И энтропия характеризует ту часть энергии системы, которую нельзя превратить в работу. l

l Постулат Планка при абсолютном нуле энтропия идеального кристалла S 0 равна нулю. l Изменение стандартной энтропии в химических реакциях S 0 (точно также как и изменение энтальпии) равно разности между суммами стандартных энтропий продуктов и реагентов, умноженных на соответствующие стехиометрические коэффициенты: l S 0 = i S 0 f, прод i S 0 f, реаг

Существует несколько формулировок второго начала: l l l теплота не может самопроизвольно переходить от более холодного тела к более горячему (Клаузиус) вечный двигатель второго рода (который превращает всю теплоту в работу) невозможен (Оствальд). Закон Больцмана: S = S 2 – S 1 = k ln (W 2/W 1) где W термодинамическая вероятность, определяемая как число микросостояний, составляющих данное макросостояние системы. Значение W тем больше, чем более неупорядоченным или неопределенным является это состояние.

Термодинамические потенциалы. l l l Энтропия определяет направление процесса в изолированной системе. Для закрытых систем аналогичными функциями являются термодинамические потенциалы: потенциал (энергия) Гиббса (G) и потенциал Гельмгольца (A): G = H – TS A = U TS Потенциал Гиббса характеризует часть энергии системы, которая может быть превращена в работу в изобарно изотермических условиях. Аналогично – потенциал Гельмгольца – для изохорно изотермических условий. G = H – T S Если для какого либо процесса G 0, то он может идти в прямом направлении, если G 0 – возможен обратный процесс. Если G = 0, система находится в положении равновесия.

Химический потенциал l l При протекании реакции в открытых системах может меняться состав и масса каждого компонента. Тогда учесть это можно с помощью еще одного потенциала – химического. Хим. потенциал i го компонента системы i определяется соотношением: l G/ ni = d I , где ni – число молей этого компонента. Химический потенциал определяет переход массы системы из одного компонента в другой. Массообмен происходит вплоть до выравнивания химических потенциалов во всем объеме. Для реакций – при достижении равновесия происходит выравнивание химических потенциалов. Тогда G: l G = прод ni I реаг ni I А химический потенциал каждого компонента равен: l I = I 0 + RT ln ai , где ai – активность (концентрация) этого компонента, а I 0 – стандартный химический потенциал вещества.

Химическая кинетика. Формальная кинетика. Для реакции A + B C ее скорость v есть: v = d[A]/dt = d[B]/dt = d[C]/dt l В общем случае для реакции a. A + b. B + c. C + … скорость реакции связана с концентрациями по закону действующих масс: v = k [A]a[B]b[C]c … l Закон действующих масс: скорость химической реакции равна произведению константы скорости на концентрации реагентов в степенях соответствующих стехиометрических коэффициентов. l

Равновесие. l l Для обратимой реакции a. A + b. B c. C + d. D в соответствии с законом действующих масс скорость прямой реакции равна v пр = kпр [A]a[B]b , а скорость обратной реакции vобр = kобр [C]c[D]d. Тогда в условиях равновесия v пр = vобр, или kпр / kобр = [C]c[D]d / [A]a[B]b = Kр l Величина Kр равная отношению констант скорости прямой и обратной реакции носит название константы равновесия.

Изотерма химической реакции. l До достижения равновесия: G = прод ni I реаг ni I Подставим в это выражение I = I 0 + RT ln ai для каждого реагента. После приведения подобных членов получим: G = (c C 0 + d D 0 a A 0 b B 0) + RT(c ln [C] + d ln [D] – a ln [A] – b ln [B]) При достижении равновесия G = 0, тогда (c C 0 + d D 0 a A 0 b B 0) = RT(c ln [C 0] + d ln [D 0] – a ln [A 0] – b ln [B 0]) где Сi 0 – равновесные значения концентраций. Но отношение концентраций под логарифмом в левой части этого уравнения равно константе равновесия Kр. То есть, (c C 0 + d D 0 a A 0 b B 0) = RT ln Kр

Изотерма химической реакции. Тогда получаем уравнение изотермы (уравнение Вант Гоффа): G = RT { ln ([C]c[D]d / [A]a[B]b) – ln Kр} которое позволяет определить направление реакции до достижения равновесия.

Молекулярность реакции. l Молекулярность химической реакции – это число реагирующих молекул. По молекулярности реакции делятся на моно- би- и тримолекулярные. К мономолекулярным относятся реакции типа: A B или A B + C. Это реакции перестройки структуры (диспропорционирования) или распада (разложения) молекулы. Бимолекулярные реакции типа A + B С или 2 A В. Значительно более редки тримолекулярные реакции, так как для их осуществления требуется столкновение сразу трех частиц, что маловероятно.

Порядок реакции. l Порядок реакции равен сумме степеней при концентрациях в уравнении для скорости реакции. Порядок реакции может быть нулевым, первым, вторым, третьим, а также дробным и любым другим. Порядок и молекулярность реакции могут совпадать только для простых одностадийных реакций, которые протекают именно так, как записано в уравнении реакции.

Причины несовпадения порядка и молекулярности. l Рассмотрим реакцию A + B С. Для нее кинетическое уравнение: v = k [A] [B] и это бимолекулярная реакция второго порядка. Но если [A] [B], то вещество В в ходе реакции расходуется полностью, тогда как концентрация вещества А практически не изменяется, то есть [A] = const. Тогда произведение константы скорости на [A] есть величина постоянная и ее можно считать новой константой скорости: v = k [A] [B] = k [B]. Таким образом, бимолекулярная реакция при условии [A] [B] становится реакцией первого порядка.

Кинетические особенности простейших одностадийных реакций 1. Реакции нулевого порядка. l l Для реакции нулевого порядка кинетическое уравнение: d. C/dt = k Разделим переменные и проинтегрируем: d. C = k dt C = k t + D, где D – константа интегрирования. Ее значение определим из начальных условий при t = 0: C 0 = D (C 0 – начальная концентрация). Окончательно интегральная форма кинетического уравнения для реакции нулевого порядка принимает вид: l C 0 C = kt Отсюда период полупревращения (T 1/2 время, за которое концентрация реагирующих веществ изменяется в 2 раза) для реакции нулевого порядка T 1/2 = С 0 / 2 k, то есть он пропорционален начальной концентрации.

2. Реакции первого порядка. l l Для реакции первого порядка кинетическое уравнение: d. C/dt = k C Как и раньше, разделим переменные и проинтегрируем: d. C/C = k dt ln C = k t + D , Начальные условия: при t = 0 ln C 0 = D (обозначения те же). Интегральная форма кинетического уравнения для реакции первого порядка принимает вид: ln (C 0 / C) = kt Период полупревращения для реакции первого порядка T 1/2 = ln 2 / k и не зависит от начальной концентрации.

3. Реакции второго порядка. l l Кинетическое уравнение здесь имеет вид: d. C/dt = k C 2 Далее: d. C/C 2 = k dt 1/C = k t + D , Значение D из начальных условий при t = 0: 1/C 0 = D. И интегральная форма кинетического уравнения для реакции второго порядка: 1/С – 1/C 0 = kt Для этой реакции T 1/2 = (k C 0) 1, то есть обратно пропорционален начальной концентрации.
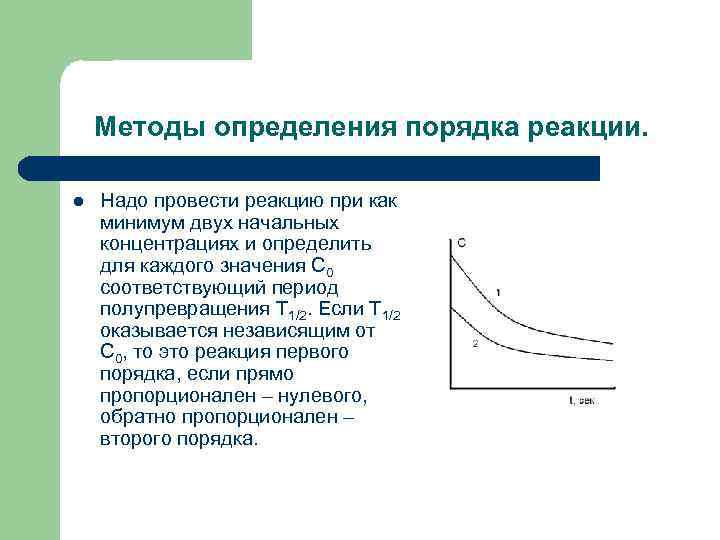
Методы определения порядка реакции. l Надо провести реакцию при как минимум двух начальных концентрациях и определить для каждого значения С 0 соответствующий период полупревращения Т 1/2. Если Т 1/2 оказывается независящим от С 0, то это реакция первого порядка, если прямо пропорционален – нулевого, обратно пропорционален – второго порядка.

Определение порядка реакции по спрямлению кинетических кривых l Другой способ определения порядка реакции заключается в подборе координат, в которых кинетические кривые спрямляются. Так для реакции первого порядка кинетические кривые спрямляются в координатах ln C t, а для реакции второго порядка – в координатах 1/C t. При этом тангенс угла наклона прямой в обоих случаях пропорционален соответствующей константе скорости (см. интегральные формы кинетических кривых).

Зависимость константы скорости от температуры. l правило Вант-Гоффа: - повышение температуры на 100 вызывает увеличение константы скорости в 2 4 раза. Любая реакция протекает через некие стадии, называемые элементарным актом. Элементарным актом реакции называется единичный акт взаимодействия или превращения частиц (молекул, радикалов, ионов, атомов), в результате которого образуются новые частицы продуктов реакции или промежуточных соединений: A B +C [A…B…C] A + B C
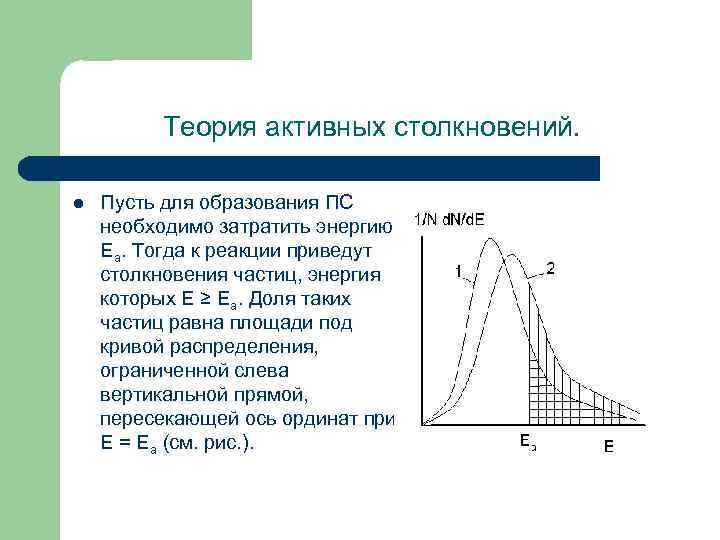
Теория активных столкновений. l Пусть для образования ПС необходимо затратить энергию Еа. Тогда к реакции приведут столкновения частиц, энергия которых Е ≥ Еа. Доля таких частиц равна площади под кривой распределения, ограниченной слева вертикальной прямой, пересекающей ось ординат при Е = Еа (см. рис. ).

Уравнение Аррениуса. l Зависимость константы скорости от температуры : k = Z exp ( Еа / RT ) где параметр Z называется предэкспоненциальным множителем, а Еа – энергией активации. Энергия активации – это минимальная энергия, которой должны обладать сталкивающиеся частицы чтобы произошла реакция.
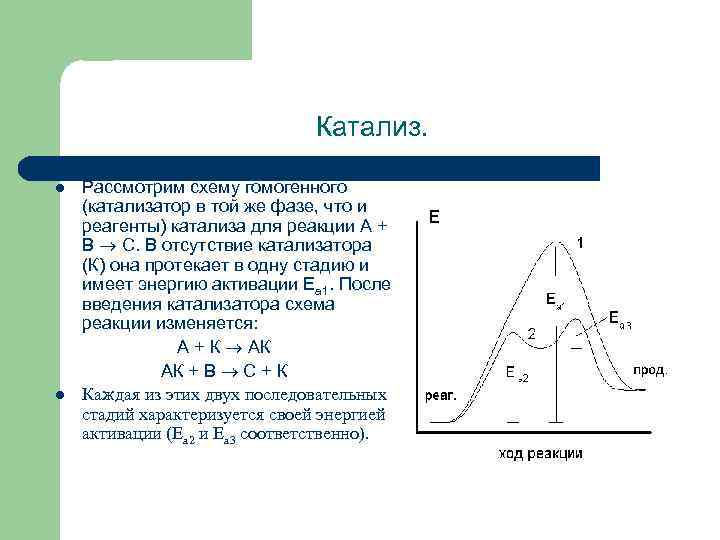
Катализ. l l Рассмотрим схему гомогенного (катализатор в той же фазе, что и реагенты) катализа для реакции A + B C. В отсутствие катализатора (К) она протекает в одну стадию и имеет энергию активации Еа 1. После введения катализатора схема реакции изменяется: A + К АК AК + B C + К Каждая из этих двух последовательных стадий характеризуется своей энергией активации (Еа 2 и Еа 3 соответственно).

АВТОКАТАЛИЗ l l l Наиболее распространенным примером гомогенного катализа является кислотный катализ, при котором катализатором является катион водорода Н+. Гидролиз: СН 3 СООС 2 Н 5 + Н+ СН 3 СООН+С 2 Н 5+ Н 2 О СН 3 СООН + С 2 Н 5 ОН + Н+ l В нейтральной среде: l СН 3 СООС 2 Н 5 + Н 2 О СН 3 СООН + С 2 Н 5 ОН

Ферментативный катализ. Схема k 1 E + S ES k 1 k 2 ES → E + P Для полной характеристики ферментативного процесса введено понятие о константе Михаэлиса (Km): Km = (k 1 + k 2) / k 1 , которая является отношением суммы констант скоростей расходования комплекса в двух направлениях к константе скорости его (комплекса) образования. В ходе ферментативной реакции энзим существует в двух формах – в свободной E и связанной ES. Скорость ферментативной реакции описывается следующим уравнением: V = Vmax[S] / (Km + [S]) Здесь представлена зависимость начальной скорости реакции V от концентрации субстрата [S] при постоянной концентрации фермента [E]. Vmax = k 2 [E]

Фазовые равновесия l l l Систему, состоящую из нескольких фаз, называют гетерогенной, а равновесие, устанав ливающееся в такой системе, — гетерогенным или фазовым. Компонентом называют индивидуальное химическое вещество, которое является составной частью системы, может быть выделено из нее и существовать самостоятельно. Числом компонентов (К) называют наименьшее число индиви дуальных химических веществ (компонентов), необходимое для формирования всех фаз термодинамической системы.

l Каждый компонент может существовать независимо от других компонентов. l Не все составные части системы учитываются при расчете числа компонентов. Например, в водном растворе поваренной соли имеется несколько видов частиц (Н 2 О, Н+, Сl-, ОН- и Na+), но всего два компонента (Na. Сl и Н 2 О). l Если вещества, образующие систему, не взаимодействуют друг с другом, то число компонентов равно числу R веществ в системе. При химических взаимодействиях K меньше R на число связей g между веществами, то есть на число независимых уравнений реакции. Например, в системе Са. СО 3 = Са. О + СО 2 g = 1, и соответственно К = 3 – 1 = 2.

Расчет числа степеней свободы l l l Состояние системы характеризуют числом степеней свободы (вариантностью). Число степеней свободы (С) – это число термодинамических параметров, определяющих состояние системы, которые можно изменять не изменяя при этом числа и природы фаз в системе. Правило фаз Гиббса: С=К–Ф+n

Однокомпонентные системы l при фазовых переходах (равновесие Тв Ж, или Ж Г): d. P/d. T = Hфп / (Tфп Vфп) Это уравнение Клапейрона – Клаузиуса. Если один компонент газ, то Vфп = Vг d. P/d. T = P Hфп / (RTфп)

Если пренебречь зависимостью Hфп от Т, то: ln ( P 2 / P 1 ) = Hфп/ R ( 1/T 1 – 1/T 2 )
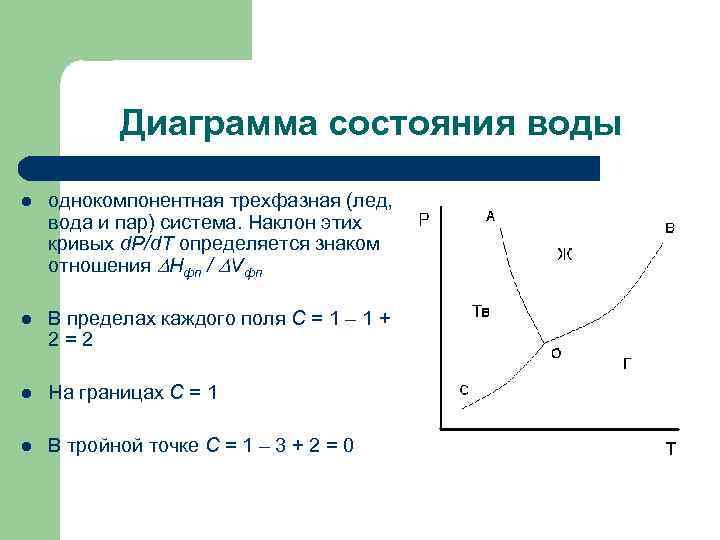
Диаграмма состояния воды l однокомпонентная трехфазная (лед, вода и пар) система. Наклон этих кривых d. P/d. T определяется знаком отношения Hфп / Vфп l В пределах каждого поля С = 1 – 1 + 2=2 l На границах С = 1 l В тройной точке С = 1 – 3 + 2 = 0

Растворы l l Растворы бывают истинными и коллоидными. В истинных растворах растворенное вещество содержится в виде атомов, молекул или ионов, в коллоидном – виде частиц другой фазы. Истинные растворы бывают идеальные (если в них нет взаимодейсвия компонентов) и реальные.

l Массовая доля ( i) – отношение массы i го компонента к общей массе системы. Массовый процент – масса i го растворенного вещества (в г) в 100 г раствора. l Объемная доля ( i) отношение объема i го компонента к общему объему системы. Мольная доля (Mi) – отношение количества молей i го компонента к общему числу молей системы. Моляльность (моляльная конценрация – mi) – отношение числа молей i го вещества к массе (в кг) растворителя. Молярность (молярная концентрация – сi) – отношение числа молей i го вещества к объему системы. Молярная концентрация эквивалента – отношение массы вещества в молярных массах эквивалента к объему системы. Молярная масса эквивалента – это произведение молярной массы на фактор эквивалентности (см. курс аналитической химии). l l

Законы идеальных растворов l Закон Вант-Гоффа: осмотическое давление пропорционально концентрации c: = с RT l Закон Рауля – относительное понижение давления насыщенного пара растворителя над раствором равно мольной доле растворенного вещества. (P 0 – P) / P 0 = M

l Если растворенное вещество летучее: Р = М АР А 0 + М ВР В 0 Но МА + МВ = 1, тогда Р = РА 0 + МВ (РВ 0 - РА 0 )

Температуры кипения и замерзания растворов l Уравнение Клапейрона Клаузиуса: P/PA 0 = Hисп Т / (R (Tкип 0)2) Но P/PA 0 = МВ , МВ = m. B / (m. B + m. A) и m. A = 1000/ А. Тогда Ткип = R (Tкип 0)2 (1000 lкип)-1 m. B = Кэб m. B Аналогично : Тз = Кз m. B

Для реальных растворов Для электролитов: (P 0 – P) / P 0 =i M , где i = 1 + ( - 1) изотонический коэффициент (коэффициент Вант Гоффа). Тогда: Ткип = i Кэб m. B и Т з = i К з m. B

Для реальных растворов двух летучих жидкостей l 1. Если энергия А В больше А А и В В (при смешении нагреваются) l 2. Если энергия А А и В В больше А В (при смешении охлаждаются)

Кривые охлаждения двухкомпонентных систем

Фазовые равновесия в двухкомпонентных гетерогенных системах Неизоморфные системы l Состав фаз – из чего состоит каждая фаза Соотношение фаз – массовые доли каждой фазы: доля твердой фазы = СО/CD доля жидкой фазы = ОD/CD l
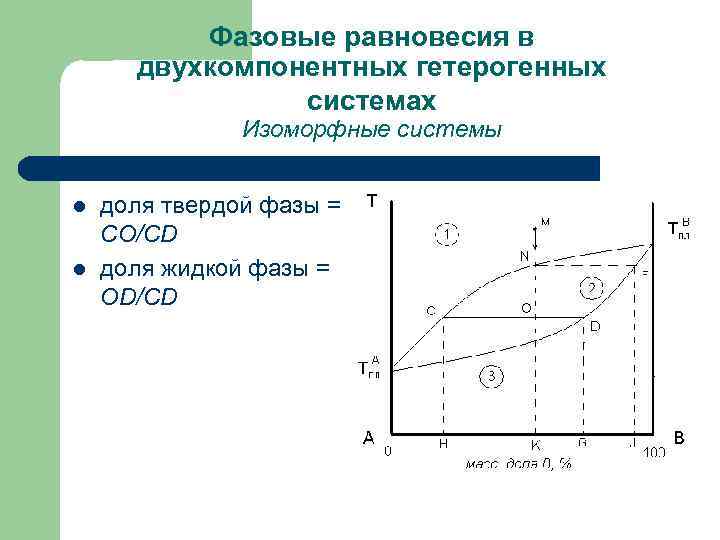
Фазовые равновесия в двухкомпонентных гетерогенных системах Изоморфные системы l l доля твердой фазы = СО/CD доля жидкой фазы = ОD/CD

Электрохимия Диссоциация и сольватация l l Для кристалла Na. Cl Hреш > 0 В растворе - ионы Na+ и Cl- Hсол 0 l Молекула воды – диполь:

l Рассмотрим диссоциацию уксусной кислоты: l CH 3 COOH H+ + CH 3 COO— l Для нее: l КД = [H+] [CH 3 COO—] / [CH 3 COOH] l Но [H+] = [CH 3 COO—] = с, тогда получаем закон разбавления Оствальда : l КД = 2 С / (1 — ) И при 1 получаем: l = (КД / С )1/2 l

Электропроводность растворов l Удельная электропроводность ( ) – это электропроводность 1 м 3 раствора, помещенного между двумя параллельными электродами площадью 1 м 2 на расстоянии 1 м. l Эквивалентная электропроводность ( ) – это электропроводность раствора, содержащего одну молярную массу эквивалента (1 кг экв) и помещенного между одинаковыми электродами, расположенными на расстоянии 1 м.

l электропроводность пропорциональна силе токов, создаваемых при данных условиях движением катионов (i. K) и анионов (i. A). Эти токи, в свою очередь, пропорциональны скорости ионов (UK и UA): i. K = С F UK и i. А = С F UА. Тогда: l l = С F ( UK + UA ) = С ( l. K + l. A ) Где l. K и l. A – подвижность (Ом. м 2/моль)

l Значения l. K и l. A для всех ионов (4 – 7)*10 -3, но для ионов ОН— и Н+ она 20 и 35*10 -3. l Эстафетный механизм миграции: Н 3 О + + Н 2 О + Н 3 О + ОН— + Н 2 О + ОН—
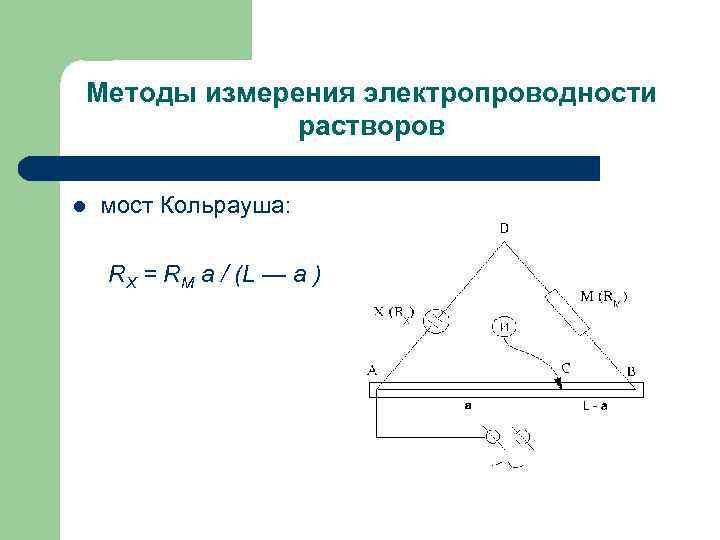
Методы измерения электропроводности растворов l мост Кольрауша: RX = RM a / (L — a )
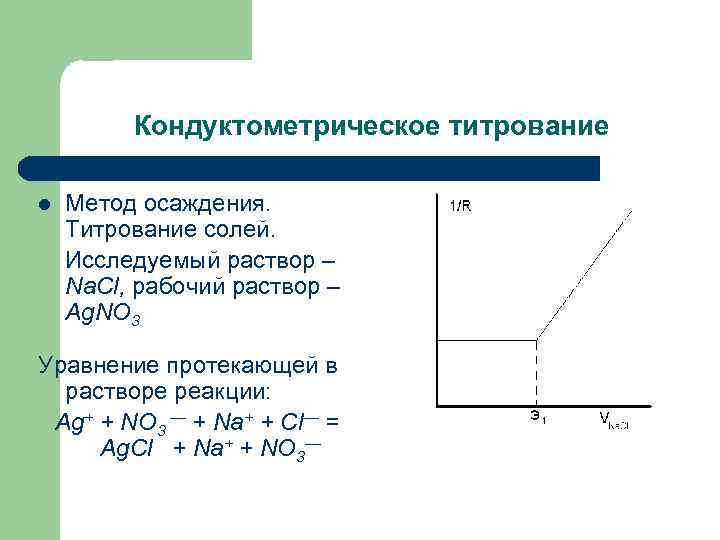
Кондуктометрическое титрование l Метод осаждения. Титрование солей. Исследуемый раствор – Na. Сl, рабочий раствор – Ag. NO 3 Уравнение протекающей в растворе реакции: Ag+ + NO 3 — + Na+ + Cl— = Ag. Cl + Na+ + NO 3—
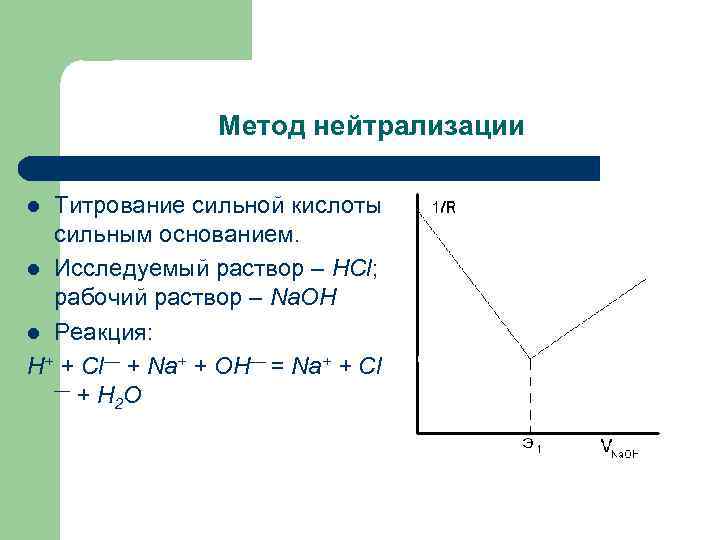
Метод нейтрализации Титрование сильной кислоты сильным основанием. l Исследуемый раствор – HCl; рабочий раствор – Na. OH l Реакция: H+ + Cl— + Na+ + OH— = Na+ + Cl — + H O 2 l
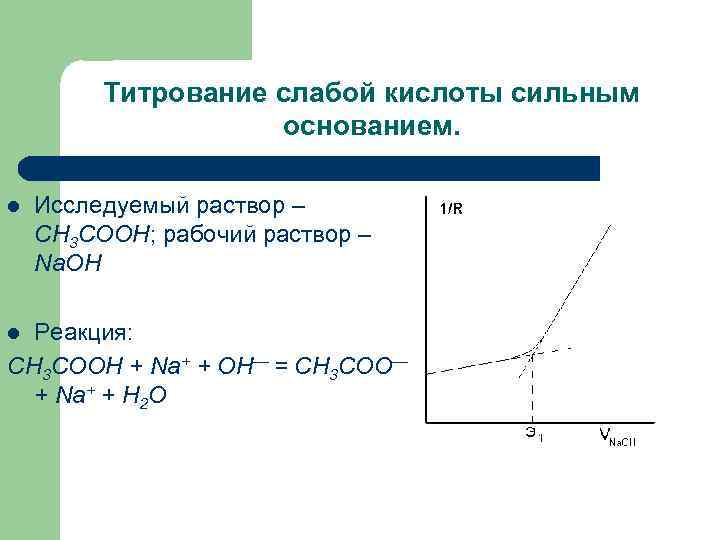
Титрование слабой кислоты сильным основанием. l Исследуемый раствор – CH 3 COOH; рабочий раствор – Na. OH Реакция: CH 3 COOН + Na+ + OH— = CH 3 COO— + Na+ + H 2 O l

Электродные процессы и электродвижущая сила ДЭС и изменение потенциала на поверхности Ag в растворе Ag. NO 3.

Работа переноса заряда в одной фазе z F , где z – заряд катиона, F – число Фарадея, – потенциал. l l l В условиях равновесия между фазами: 1 + z F 1 = 2 + z F 2 где 1 и 2 – значения хим. потенциалов катиона в решетке и растворе. Отсюда можно рассчитать значение скачка потенциала на поверхности металла: = ( 1 2) / z F Для раствора = 0 + RT ln a. К, где a. К – активность катиона в растворе. Хим. потенциал иона в кристаллической решетке – величина постоянная, тогда: = 0 + (RT / z F) ln a. К l где 0 – стандартный электродный потенциал при a. К = 1. Это уравнение Нернста Тюрина.

Когда есть окисленная и восстановленная форма, уравнение Нернста Тюрина принимает вид: = 0 + (RT / z F) ln (aок / aвос) Здесь aок и aвос – активности окисл. и восст. форм. l l l Виды электродов. Электрод первого рода металл погруженный в раствор собственной соли. Обозначение: металл|соль (Ag|Ag. NO 3 или Cu|Cu. SO 4). Окислительно восстановительный процесс типа: l Ag+ + e- Ag 0 или Cu 2+ + 2 e- Cu 0 Эти электроды обратимы по катиону. Направление процесса зависит от направления тока в электроде. Процесс, идущий слева направо – восстановление, обратный – окисление. Достоинство простота, недостаток – нестабильность.

Электроды второго рода металл, покрытый малорастворимой солью этого же металла и погруженный в раствор соли с тем же анионом, что и малорастворимая соль. l хлорсеребряный и хлорсвинцовый электроды обозначаются: Ag|Ag. Cl|KCl и Pb|Pb. Cl 2|KCl. они обратимы по аниону и на электроде происходит реакция: Ag. Cl + e- Ag 0 + Clуравнение Нернста Тюрина: = 0 - (RT / z F) ln a. А

окислительно-восстановительные электроды l металл является только переносчиком электронов, процесс же окисления – восстановления протекает между ионами в растворе. Потенциалопределяющий процесс записывают в виде Ох + ze- Red l Хингидронный электрод : Pt|X, H 2 X, H+ или Pt|Хг, H+. Х + 2 Н+ + 2 е- Н 2 Х l Уравнение Нернста Тюрина для него принимает вид: l = 0 + (RT / z F) ln ([X] [H+]2 / [H 2 X] ) = 0 + (RT / F) ln ([H+] ) = 0 – (2. 303 RT / F) р. Н

Водородный электрод 2 Н+ + 2 е- Н 2 Уравнение Нернста Тюрина : l l Н 2 = 0 Н 2 + (RT / z F) ln ([H+]2 /РН 2) Н 2 = - (2. 303 RT / F) р. Н = = - 0. 0591 p. H

Гальванические элементы l Гальванический элемент устройство из двух электродов, в котором химическая энергия преобразуется в электрическую l l В нем внешняя и внутренняя цепь Обозначение первый электрод||второй электрод l Элемент Якоби Даниэля: Cu|Cu. SO 4||Zn. SO 4|Zn или Cu|Cu. SO 4||KCl||Zn. SO 4|Zn

Электродые процессы l l На Zn электроде (термодинамически необратимо): Zn 0 Zn 2+ + 2 e- (окисление) На Cu электроде (термодинамически необратимо): Сu 2++ 2 е- Сu 0 (восстановление) И суммарный токообразующий процесс: Zn 0 + Сu 2+ Zn 2+ + Сu 0 При замыкании цепи элемента возникает ЭДС (Е): Е = + - -

Определение ЭДС гальванических элементов l В состоянии равновесия: ЕX = ЕW АС 1/АС

Водородная шкала стандартных потенциалов l 0 = 0 для водородного электрода. l В шкале верхние места Li+, Li; Zn 2+, Zn. Это наиболее отрицательные ионы по отношению в водороду. l Расположенные в порядке уменьшения отрицательности, стандартные потенциалы электродов образуют ряд напряжений металлов.
физхимия.ppt