FIXED-INCOME SECURITIES LECTURE 5 Term Structure of Interest

FIXED-INCOME SECURITIES LECTURE 5 Term Structure of Interest Rates 1

1、Factors that affect risk premium Yn = Rf, n + DP + LP + TA + CALLP + COND Where: Yn = yield of an n-day security Rf, n = yield on an n-day Treasury (risk-free) security DP = default premium (credit risk) LP = liquidity premium TA = adjustment for tax status CALLP = call feature premium COND = convertibility discount 2

Factors that affect risk premium n n n n Interest rate=base interest rate+risk premium Type of issuers The issuer’s perceived creditworthiness The term of the instruments Embedded option Taxability liquidity 3

Taxability of interest n n qualified municipal bonds are exempts from federal taxes. After tax yield = pretax yield (1 - marginal tax rate) 4

Determinants of the Yield Curve n n Federal Reserve sets a target level for the fed funds rate - the rate at which depository institutions make uncollaterized overnight loans to one another. Long-term rates reflect expectations of future rates and can be influenced by the outlook for monetary policy. 5

2、Term Structure of IR n n n If we knew the future IR: 0(Today) 8% 1 10% 2 11% 3 11% 6

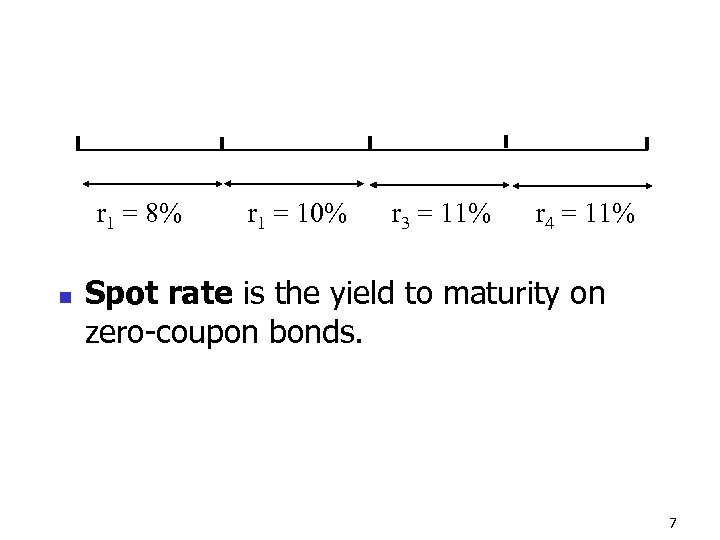r 1 = 8% n r 1 = 10% r 3 = 11% r 4 = 11% Spot rate is the yield to maturity on zero-coupon bonds. 7

SPOT RATE n SPOT RATE EQUATION: where D(t, T)= the t time market price of a pure discount bond maturing in(T-t) years， the maturity value is 1 ， = the spot rate 8

Discount factor, Spot rate Is the time t price of a zero coupon bond with face value = $1 That is D(0, T) is today’s discount factor Spot rate That is R(0, T) is today’s spot rate(today’s zero rate). 9

DISCOUNT FACTORS $X = price of bond with t-year maturity, $Y = face value = t-year discount factor = Value today of a dollar to be receive in t-years = $X/ $Y m periods per year compounding: Continuous compounding: 10

Future versus Spot Rates s 1 = 8% r 2 = 10% r 3 = 11% r 4 = 11% s 1= 8% s 2= 8. 995% s 3= 9. 66% s 4= 9. 993% 11

Do not use yield curve to price bonds n n n They can not be priced by discounting cash flow with the same yield because of different structure of CF. The Principle of No Arbitrage or The Law of One Price Use spot rates (yield on zero-coupon Treasuries) instead! 12

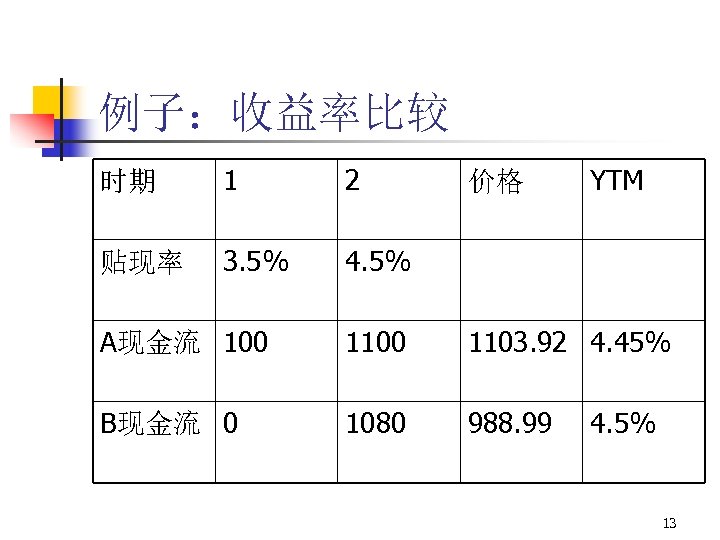例子：收益率比较 时期 1 2 贴现率 3. 5% 4. 5% 价格 YTM A现金流 100 1103. 92 4. 45% B现金流 0 1080 988. 99 4. 5% 13

Bond Yields and Spot Rates n n we can construct coupon bonds from portfolios of zeroes, and we can construct zeroes from portfolios of coupon bonds. This means that, in the absence of arbitrage, the prices of zeroes imply prices for coupon bonds and the prices of coupon bonds imply prices for zeroes. 14

Continue n Notice that the yield is a blend or a kind of average of the different zero rates associated with the cash flows. In other words, the yield must be between the highest and lowest spot rates. 15

FORWARD RATE n DEFINITION: the interest rate today that will be paid on money to be n n n borrowed at some specific future date and to be repaid at a specific more distant future date 远期利率是指从未来某个日期开始的远期债 务合约所要求的利率。 16

FORWARD RATE 1 假设某个 1年期零息债券的即期利率为 8%， 而另一个两年期的零息债券的即期利率 则为 10%。如果投资者投资1元钱在一个 两年期的零息债券上，两年后将获得 1× （1. 10） 2元。那么，从现在看，第 2年 （第 2年初到第 2年末）的远期利率是多 少呢？第 2年的远期利率可计算如下： [1×（1. 10）2/1. 08]-1=12. 04% 17

FORWARD RATE 2 f 1, 2 is the forward rate from year 1 to year 2 (1+r 3)3=(1+r 1)(1+f 1, 3)2= (1+r 1)(1+f 1, 2)(1+f 2, 3) f 1, 3 is the annualized forward rate from year 1 to year 3 18

FORWARD RATE 3 n More generally for the link between years t-1 and t: 19

Continuous Compounding (simpler formula): 20

3 、YIELD CURVES n DEFINITION: a graph that shows the YTM for zero-coupon Treasury securities of various terms (maturities) on a particular date 21

YIELD CURVES n YIELD CURVES AND TERM STRUCTURE n yield curve provides an estimate of n n the current TERM STRUCTURE OF INTEREST RATES yields change daily as YTM changes 22

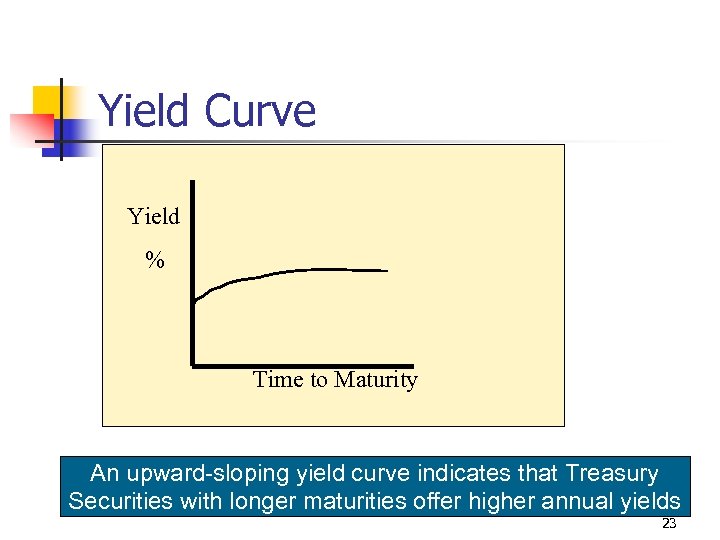Yield Curve Yield % Time to Maturity An upward-sloping yield curve indicates that Treasury Securities with longer maturities offer higher annual yields 23

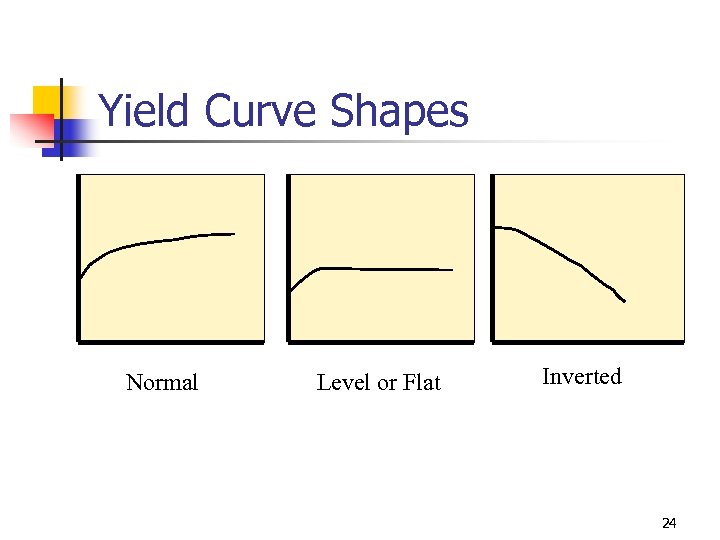Yield Curve Shapes Normal Level or Flat Inverted 24

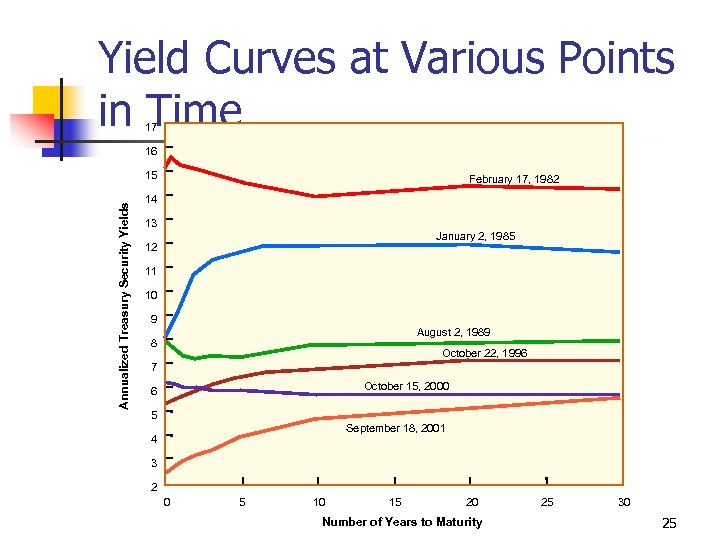Yield Curves at Various Points in Time 17 16 Annualized Treasury Security Yields 15 February 17, 1982 14 13 January 2, 1985 12 11 10 9 August 2, 1989 8 October 22, 1996 7 October 15, 2000 6 5 September 18, 2001 4 3 2 0 5 10 15 20 Number of Years to Maturity 25 30 25

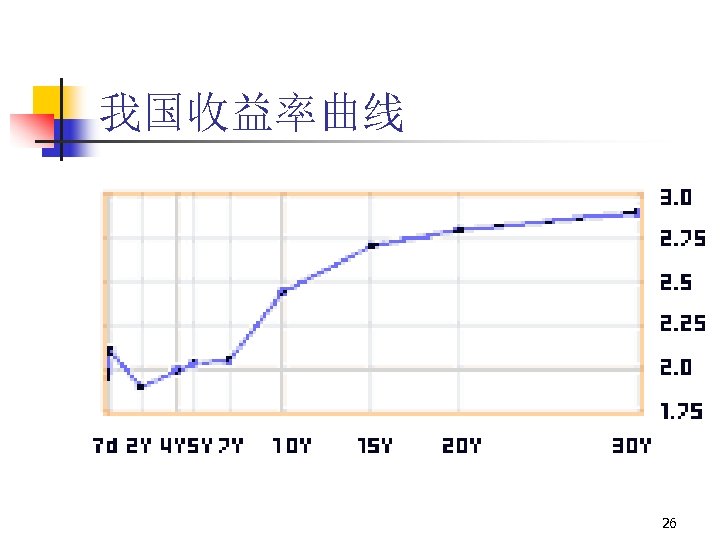我国收益率曲线 26

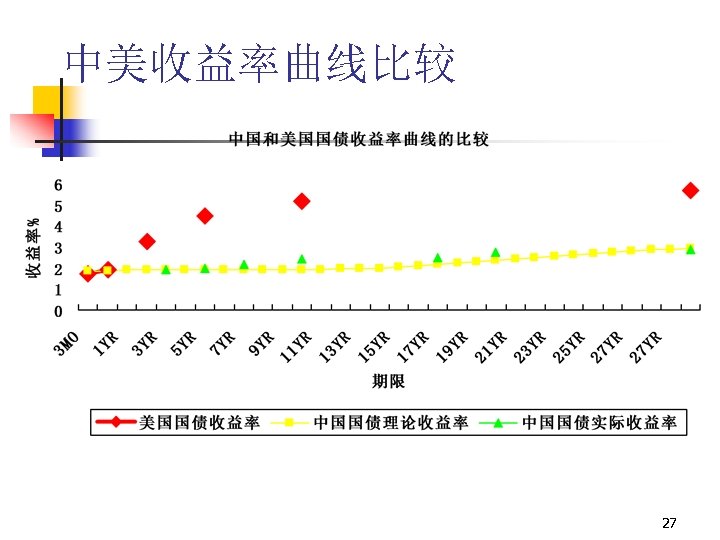中美收益率曲线比较 27

4. THE TERM STRUCTURE OF INTEREST RATES n n Term structure theory deals with the effect that time has on interest rates. It seeks to answer the question of why bonds with different maturities should have different yields. 28

TERM STRUCTURE THEORIES n THE FOUR THEORIES 1. 2. 3. 4. THE UNBIASED EXPECTATION THEORY THE LIQUIDITY PREFERENCE THEORY MARKET SEGMENTATION THEORY PREFERRED HABITAT THEORY 29

UNBIASED EXPECTATIONS n n n Basic Theory: the forward rate represents the average opinion of the expected future spot rate for the period in question in other words, the forward rate is an unbiased estimate of the future spot rate. If this theory is correct, then the shape of the yield curve is also an accurate indicator of expected future spot rates. 30

TERM STRUCTURE THEORY: Unbiased Expectations n THEORY 1: UNBIASED EXPECTATIONS n n the expected future spot rate equals the forward rate in equilibrium es 1, 2 = f 1, 2 where es 1, 2 = the expected future spot f 1, 2 = the forward rate 31

TERM STRUCTURE THEORY: Unbiased Expectations 32

TERM STRUCTURE THEORY: Unbiased Expectations n CHANGING SPOT RATES AND INFLATION n Why do investors expect rates to rise or fall in the future? n spot rates = nominal rates n because we know that the nominal rate is the real rate plus the expected rate of inflation 33

TERM STRUCTURE THEORY: Unbiased Expectations n CHANGING SPOT RATES AND INFLATION n Why do investors expect rates to rise or fall in the future? n if either the spot or the nominal rate is expected to change in the future, the spot rate will change 34

TERM STRUCTURE THEORY: Unbiased Expectations n CHANGING SPOT RATES AND INFLATION n Why do investors expect rates to rise or fall in the future? n if either the spot or the nominal rate is expected to change in the future, the spot rate will change 35

TERM STRUCTURE THEORY: Unbiased Expectations n Current conditions influence the shape of the yield curve, such that n n if deflation expected, the term structure and yield curve are downward sloping if inflation expected, the term structure and yield curve are upward sloping 36

TERM STRUCTURE THEORY: Unbiased Expectations n PROBLEMS WITH THIS THEORY: n n n upward-sloping yield curves occur more frequently Investors are not indifferent to risk Cox-Ingersoll-Ross have investigated this hypothesis and find that it is not consistent with an economic equilibrium. 37

TERM STRUCTURE THEORY: Liquidity Preference n BASIC NOTION OF THEORY n n investors primarily interested in purchasing short-term securities to reduce interest rate risk Hicks (1939) suggested that lenders demand a premium for locking up their money for long period of time. 38

TERM STRUCTURE THEORY: Liquidity Preference n BASIC NOTION OF THEORY n Price Risk n n maturity strategy is more risky than a rollover strategy to convince investors to buy longer-term securities, borrowers must pay a risk premium to the investor 39

TERM STRUCTURE THEORY: Liquidity Preference n How does this theory explain the shape of the yield curve? n rollover strategy n at the end of 2 years $1 has an expected value of $1 x (1 + s 1 ) (1 + es 1, 2 ) 40

TERM STRUCTURE THEORY: Liquidity Preference n How does this theory explain the shape of the yield curve? n whereas a maturity strategy holds that $1 x (1 + s 2 )2 n which implies with a maturity strategy, you must have a higher rate of return 41

TERM STRUCTURE THEORY: Liquidity Preference n How does this theory explain the shape of the yield curve? n Key Idea to theory: The Inequality holds (1+s 1)(1 +es 1, 2)< (1 + s 2)2 (1+s 1)(1 +es 1, 2)< (1 + s 1)（1+f 1, 2） 42

TERM STRUCTURE THEORY: Liquidity Preference n BASIC NOTION OF THEORY n Liquidity Premium Equation f 1, 2 = es 1, 2+ L 1, 2 where L is the liquidity premium 43

TERM STRUCTURE THEORY: Liquidity Preference 44

TERM STRUCTURE THEORY: Liquidity Preference n BASIC NOTION OF THEORY n Liquidity Premium n DEFINITION: the difference between the forward rate and the expected future rate 45

n n n LPT assumes that investors are not indifferent to risk. They are risk averse LPT recognises that investors demand a yield premium as compensation for investing longer-term LPT suggests that forward rates include both investors’ expectations of future spot rates and liquidity premiums. 46

n n n Since, implicit forward rates include a risk premium, then: forward rates should be higher than expected future spot rates This means that forward rates are not unbiased estimators of expected future spot rates. 47

n n With inverse yield curve, investors could still receive a risk-premium for lending long when interest rates are expected to fall. The liquidity premium causes forward rates to be consistently higher than the expected future spot rates. 48

PROBLEMS WITH LPT n n Although LPT theory is consistent with generally upward-sloping yield curve, it does not indicate the size of the risk premium Risk premium rising uniformly for all maturities may not be the case 49

TERM STRUCTURE THEORY: Liquidity Preference n SHAPES OF THE YIELD CURVE: n n n a flat yield curve means the market expects interest rates to decline an upward-sloping curve means rates are expected to any change. a downward-sloping curve means the market believes interest rates are going to decline 50

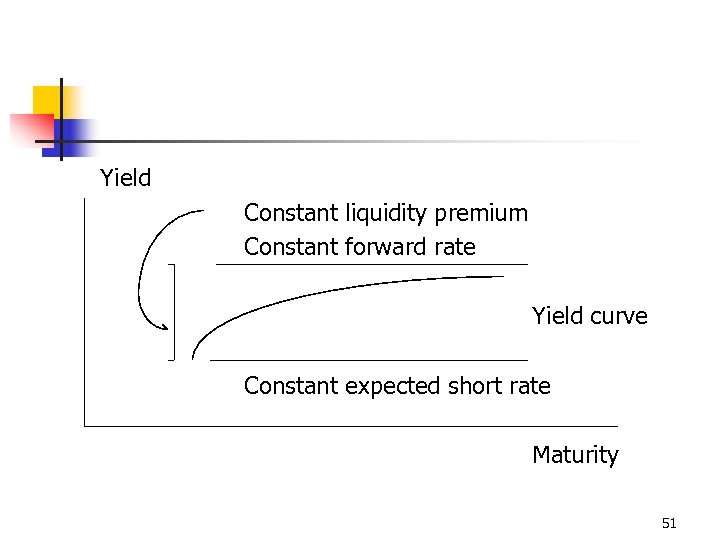Yield Constant liquidity premium Constant forward rate Yield curve Constant expected short rate Maturity 51

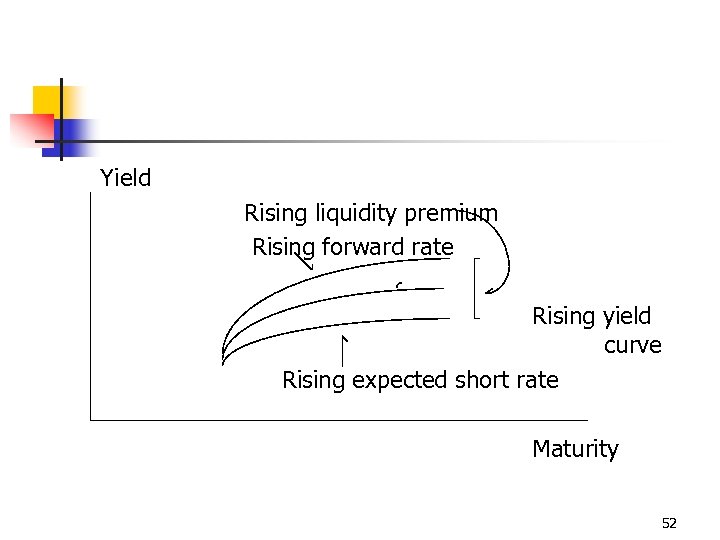Yield Rising liquidity premium Rising forward rate Rising yield curve Rising expected short rate Maturity 52

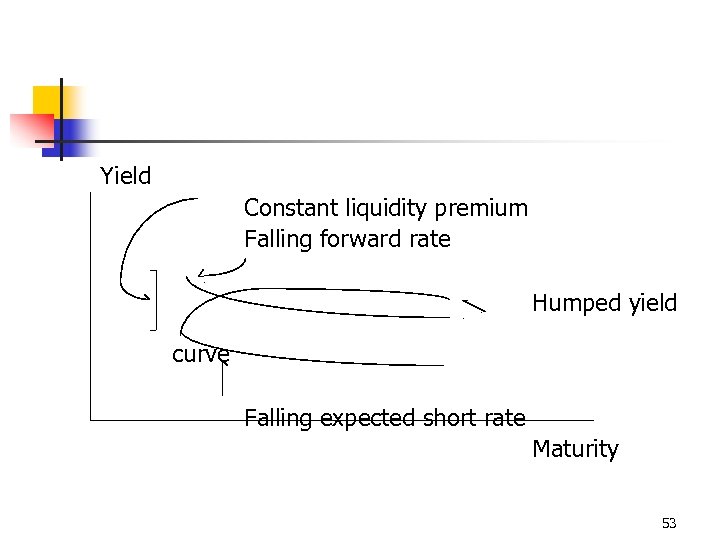Yield Constant liquidity premium Falling forward rate Humped yield curve Falling expected short rate Maturity 53

TERM STRUCTURE THEORY: Market Segmentation n BASIC NOTION OF THEORY various investors and borrowers are restricted by law, preference or custom to certain securities Theory explains the term structure of interest rates as a series of preference zones, which certain investors select depending on term to maturity. 54

The Market Segmentation Theory The market segmentation theory maintains that market participants have strong preferences for securities of a particular maturity and holds that they buy and sell securities consistent with these maturity preferences. 55

n n n Institutional investors often prefer particular maturities to match their liabilities. Banks (usually require bonds with short maturities), life insurance & pension funds (bonds with long maturities) the investors always demand specific maturities irrespective of interest rates expectations. 56

Long- and short-maturity bonds are traded in essentially distinct or segmented markets, each of which finds its own equilibrium independently. 57

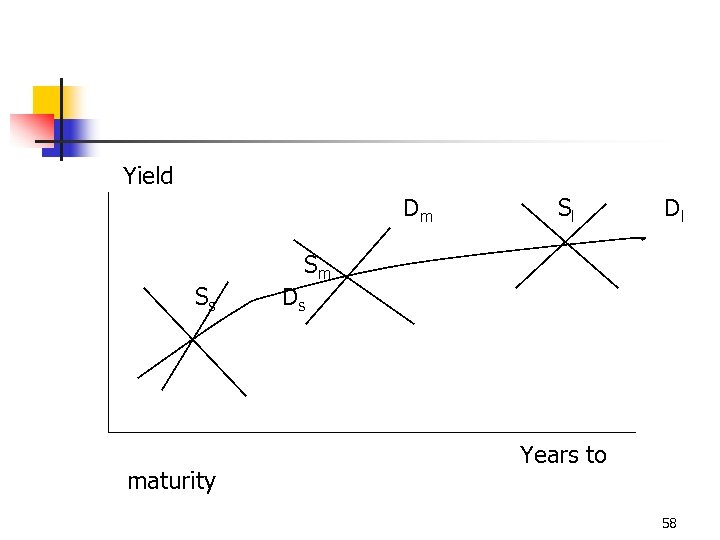Yield Dm Ss maturity Sl Dl Sm Ds Years to 58

n n According to SMH , risk aversion is strong and widespread enough, to keep borrowers and lenders in their preferred maturities. Implication: absence of arbitrage across different maturity horizon 59

TERM STRUCTURE THEORY: Market Segmentation n WHAT EXPLAINS THE SHAPE OF THE YIELD CURVE? n n Upward-sloping curves mean that supply and demand intersect for short-term is at a lower rate than longer-term funds cause: relatively greater demand for longer-term funds or a relative greater supply of shorter-term funds 60

TERM STRUCTURE THEORY: Preferred Habitat n BASIC NOTION OF THEORY: n n Investors and borrowers have segments of the market in which they prefer to operate. Theory lies between LPT and SMH 61

n PHT recognises limitations on supply for bonds with specific maturities as well as the existence of arbitrage opportunities in the market. 62

The theory argues that n n “the interest rate risk is minimised if bond maturity matches the investors planned expenditure However, investors preferred habitats are not absolute. Investors are prepared to invest in bonds with other maturities if they are adequately compensated for any additional risk exposure 63

The Preferred Habitat Theory The preferred habitat theory asserts that investors will not hold debt securities outside of their preferred habitat (maturity preference) without an additional reward in the form of a risk premium. That is, investors prefer specific maturity ranges but can be induced to switch if premiums are sufficient. 64

Preferred Habitat THEORY n When significant differences in yields exist between market segments, investors are willing to leave their desired maturity segment 65

TERM STRUCTURE THEORY: Preferred Habitat n n The term structure reflects the expectation of the future path of interest rates as well as a risk premium, but the risk premium does not necessarily rises uniformly with maturity. 66

n n The shape of the yield curve is determined by both expectations on future interest rates and a risk premium (positive or negative) to induce market participants to shift out of their preferred habitat. According to this theory, yield curves sloping up, down, being flat or humped are all possible and can be justified. 67

5、 Deriving the Zero-Coupon Yield Curve Outline n n n n General Principle Spot Rates Forward Rates Recovering the Term Structure Direct Methods Interpolation Splines 68

Yield Curve Term Structure Estimation Methods n Most popular ones are (1) Bootstrapping Method (2) Cubic-Spline Method by Mc. Culloch (1971, 1975) (3) Nelson and Siegel Exponential. Form Method (1987) 69

Last Time n n n Now, do we expect to get the same rate when borrowing/lending for a year versus 10 years? Not necessarily Term structure of interest rates 70

General Principle n n n General formula – R(0, t) is the discount rate – D(0, t) is the discount factor (present value of $1 received at date t) – Discount factor more convenient: no need to specify frequency Question: Where do we get the D(0, t) or R(0, t) from? 71

Spot Rates Q: Where do we get the D(0, t) or R(0, t) from? n – Any relevant information concerning how to price a security should be obtained from market sources n – More specifically, D(t, T) is the price at date t of a unit pure discount bond paying $1 at date T n Discount factor D(0, t) is the price of a T-Bond with unit face value and maturity t n Spot rate R(0, t) is the annualized rate on a pure discount bond: n Bad news is no such abundance of zero-coupon bonds exists in the real world n Good news is we might still be able to compute the spot rate 72

Spot Rates n n n Example of spot rate: – Consider a two-year pure discount bond that trades at $92 The two-year spot rate is: The collection of all spot rates for all maturities is: – The Term Structure of Interest Rates n 73

Recovering the Term Structure Direct Methods - Principle n Consider two securities (nominal $100): – One year pure discount bond selling at $95 – Two year 8% bond selling at $99 One-year spot rate: n Two-year spot rate: n n n 74

Recovering the Term Structure Direct Methods - Principle n n n We may “construct” a two year pure discount bond Two components: – Buy the two year bond – Shortsell. 08 units of the one year bond Cost 75

Recovering the Term Structure Direct Methods - Principle n n n Schedule of payments: This is like a two-year pure discount bond Two-year rate is again: 76

Recovering the Term Structure Direct Methods - Example n n n If you can find different bonds with same anniversary date, then you can directly get the spot rates : Coupon Maturity (year) Price Bond 1 5 1 101 Bond 2 5. 5 2 101. 5 Bond 3 5 3 99 Bond 4 6 4 100 77

Recovering the Term Structure Direct Methods - Example n n n n • Solve the following system 101 = 105 D(0, 1) 101. 5 = 5. 5 D(0, 1) + 105. 5 D(0, 2) 99 = 5 D(0, 1) + 5 D(0, 2) + 105 D(0, 3) 100 = 6 D(0, 1) + 6 D(0, 2) + 6 D(0, 3) + 106 D(0, 4) And obtain D(0, 1)=0. 9619, D(0, 2)=0. 9114, D(0, 3)=0. 85363, D(0, 4)= 0. 7890 R(0, 1)=3. 96%, R(0, 2)=4. 717%, R(0, 3)=5. 417%, R(0, 4)=6. 103% 78

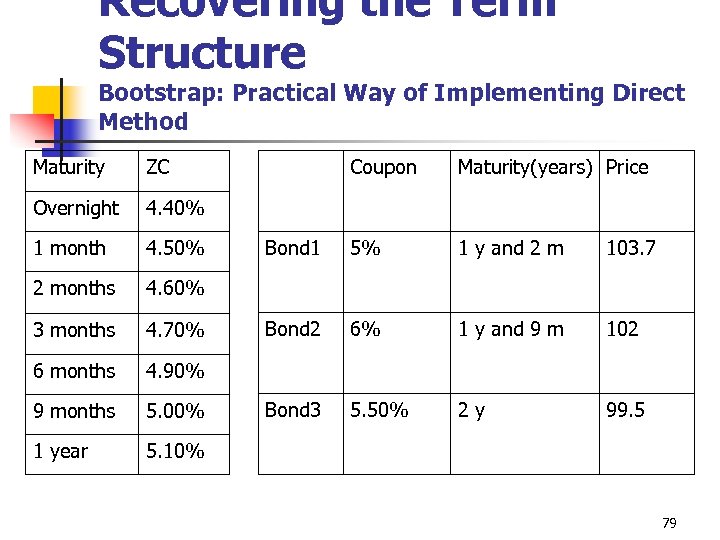Recovering the Term Structure Bootstrap: Practical Way of Implementing Direct Method Maturity ZC Overnight 4. 40% 1 month 4. 50% 2 months 4. 60% 3 months 4. 70% 6 months 4. 90% 9 months 5. 00% 1 year Coupon Maturity(years) Price Bond 1 5% 1 y and 2 m 103. 7 Bond 2 6% 1 y and 9 m 102 Bond 3 5. 50% 2 y 99. 5 5. 10% 79

Recovering the Term Structure Bootstrap: Practical Way of Implementing Direct Method n n n 1 year and 2 months rate x=5. 41% 1 year and 9 months rate y= 5. 69% 2 year rate z= 5. 69% 80

Recovering the Term Structure Interpolation - Linear n n n Interpolation – Term structure is a mapping T -> R(t, T) for all possible T – Need to interpolate Linear interpolation – We know discount rates for maturities t 1 et t 2 We are looking for the rate with maturity t such that t 1< t

Example: R(0, 3) =5. 5% and R(0, 4)=6% 82

Interpolation – Piecewise Polynomial n n n Cubic interpolation for different segments of the term structure – Define the first segment: maturities ranging from t 1 to t 4 (say 1 to 2 years) – We know R(0, t 1), R(0, t 2), R(0, t 3), R(0, t 4) The discount rate R(0, t) is defined by Impose the constraint that R(0, t 1), R(0, t 2), R(0, t 3), R(0, t 4) are on the curve 83

Recovering the Term Structure Piecewise Polynomial - Example n n n n We have computed the following rates – R(0, 1) = 3% – R(0, 2) = 5% – R(0, 3) = 5. 5% – R(0, 4) = 6% Compute the 2. 5 year rate R(0, 2. 5) = a x 2. 53 + b x 2. 52 + c x 2. 51 + d = 5. 34375% With 84

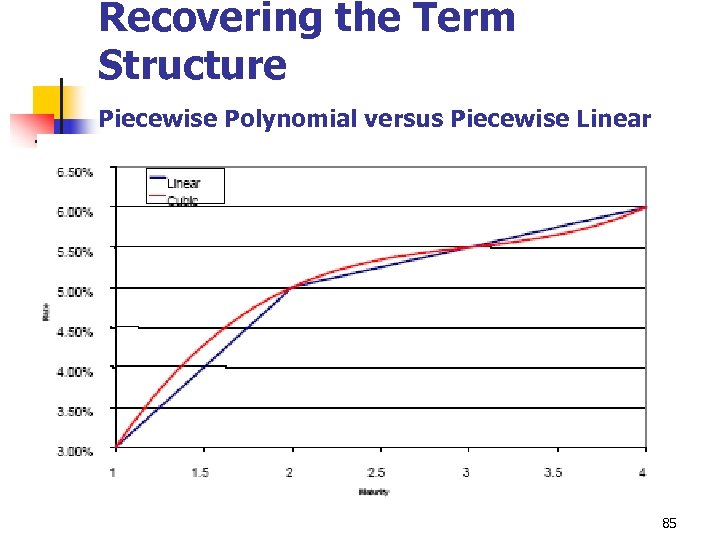Recovering the Term Structure Piecewise Polynomial versus Piecewise Linear 85

Polynomial Splines n Discount factors as polynomial splines n Impose smooth-pasting constraints n Cut down the number of parameters from 12 to 5 86

Example n n n 2006年 2月15日，票面利率为 8. 875%到 期日为 2007年 7月15日的债券价格为 106. 4元。该债券半年付息一次。 106. 4=4. 7375×d(5/12)+ 4. 7375×d(11/12)+ 104. 7375×d(17 /12) d(5/12)=d 0+c 0 (5/12)+b 0 (5/12)2 +a 0 (5/12)3 87

parsimonious models. 88