3cba0253fc1b670604e1659e1c71f4bf.ppt
- Количество слайдов: 57

 Five-Minute Check (over Lesson 12– 1) CCSS Then/Now New Vocabulary Key Concept: Angle Measures Example 1: Draw an Angle in Standard Position Example 2: Real-World Example: Draw an Angle in Standard Position Example 3: Find Coterminal Angles Key Concept: Convert Between Degrees and Radians Example 4: Convert Between Degrees and Radians Concept Summary: Degrees and Radians Key Concept: Arc Length Example 5: Real-World Example: Find Arc Length
Five-Minute Check (over Lesson 12– 1) CCSS Then/Now New Vocabulary Key Concept: Angle Measures Example 1: Draw an Angle in Standard Position Example 2: Real-World Example: Draw an Angle in Standard Position Example 3: Find Coterminal Angles Key Concept: Convert Between Degrees and Radians Example 4: Convert Between Degrees and Radians Concept Summary: Degrees and Radians Key Concept: Arc Length Example 5: Real-World Example: Find Arc Length
 Over Lesson 12– 1 Find sin , cos , and tan . A. B. C. D.
Over Lesson 12– 1 Find sin , cos , and tan . A. B. C. D.
 Over Lesson 12– 1 Find sin , cos , and tan . A. B. C. D.
Over Lesson 12– 1 Find sin , cos , and tan . A. B. C. D.
 Over Lesson 12– 1 Find csc , sec , and cot . A. B. C. D.
Over Lesson 12– 1 Find csc , sec , and cot . A. B. C. D.
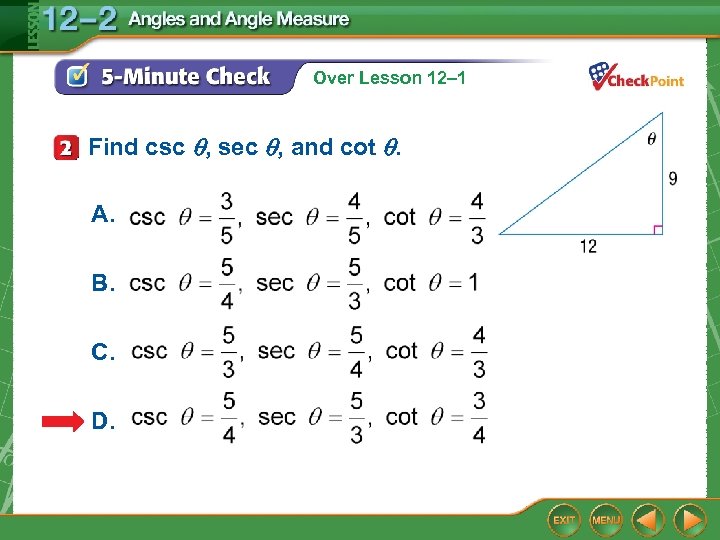 Over Lesson 12– 1 Find csc , sec , and cot . A. B. C. D.
Over Lesson 12– 1 Find csc , sec , and cot . A. B. C. D.
 Over Lesson 12– 1 Find the value of a. A. 13. 9 B. 12. 3 C. 6. 9 D. 4. 5
Over Lesson 12– 1 Find the value of a. A. 13. 9 B. 12. 3 C. 6. 9 D. 4. 5
 Over Lesson 12– 1 Find the value of a. A. 13. 9 B. 12. 3 C. 6. 9 D. 4. 5
Over Lesson 12– 1 Find the value of a. A. 13. 9 B. 12. 3 C. 6. 9 D. 4. 5
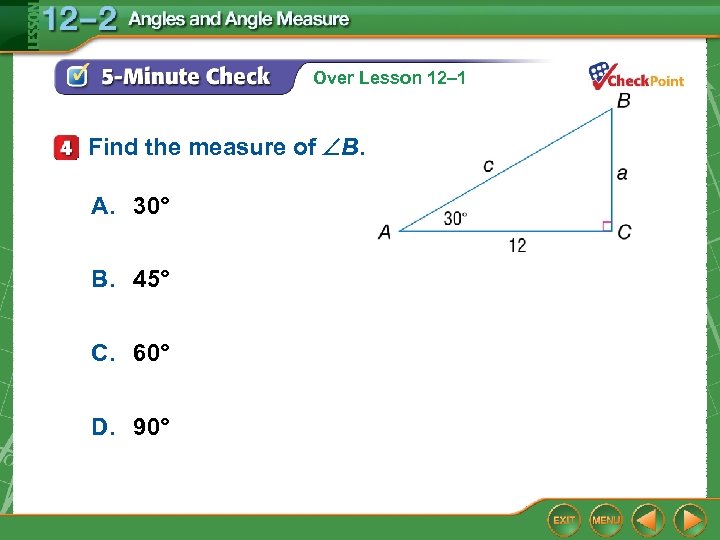 Over Lesson 12– 1 Find the measure of B. A. 30° B. 45° C. 60° D. 90°
Over Lesson 12– 1 Find the measure of B. A. 30° B. 45° C. 60° D. 90°
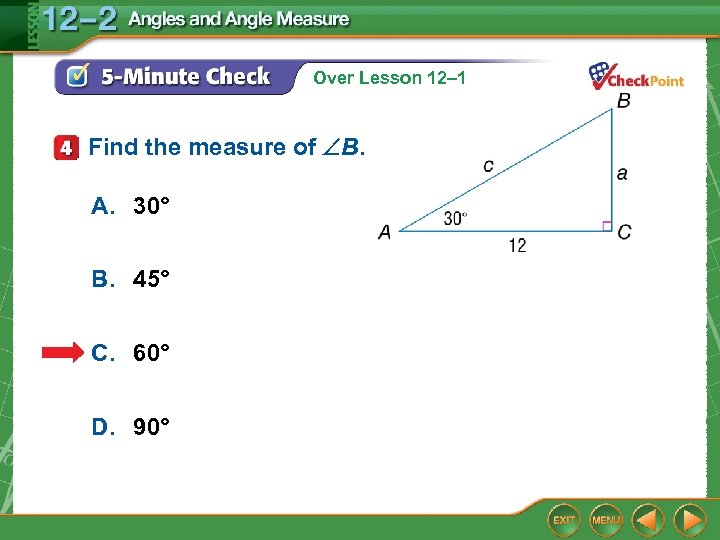 Over Lesson 12– 1 Find the measure of B. A. 30° B. 45° C. 60° D. 90°
Over Lesson 12– 1 Find the measure of B. A. 30° B. 45° C. 60° D. 90°
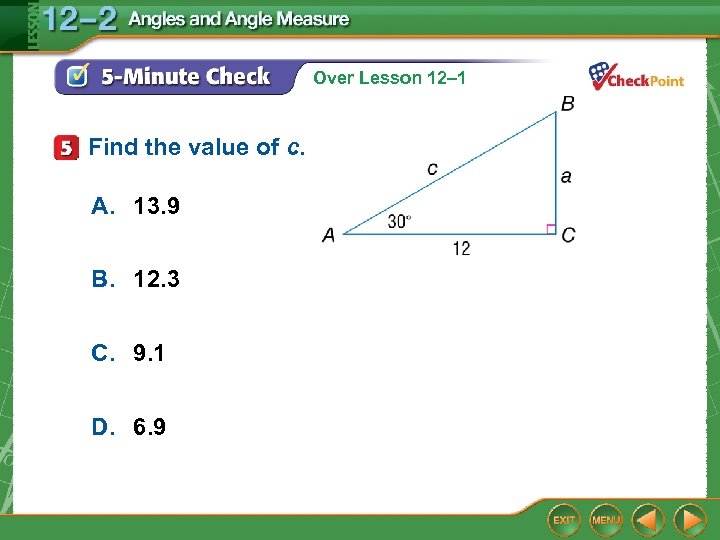 Over Lesson 12– 1 Find the value of c. A. 13. 9 B. 12. 3 C. 9. 1 D. 6. 9
Over Lesson 12– 1 Find the value of c. A. 13. 9 B. 12. 3 C. 9. 1 D. 6. 9
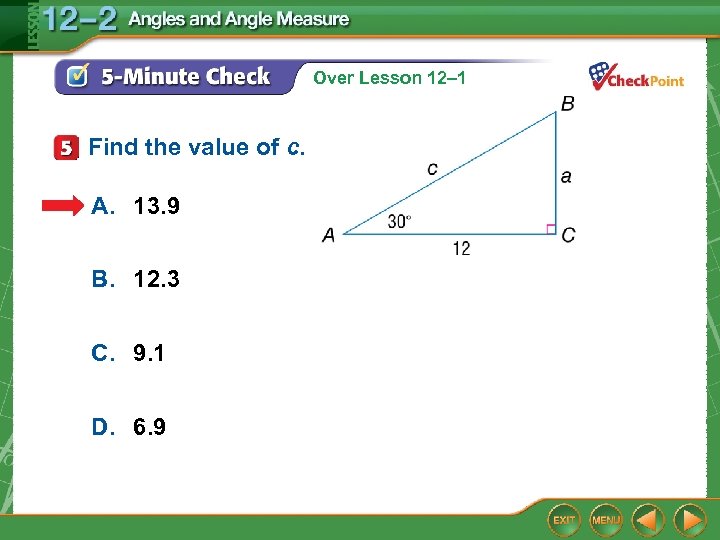 Over Lesson 12– 1 Find the value of c. A. 13. 9 B. 12. 3 C. 9. 1 D. 6. 9
Over Lesson 12– 1 Find the value of c. A. 13. 9 B. 12. 3 C. 9. 1 D. 6. 9
 Over Lesson 12– 1 David needs a ramp that rises to a height of 3 feet at a 15° angle. Write an equation for the length ℓ of the ramp. A. ℓ = 3 sin 15° B. ℓ = 3 cos 15° C. ℓ D. ℓ
Over Lesson 12– 1 David needs a ramp that rises to a height of 3 feet at a 15° angle. Write an equation for the length ℓ of the ramp. A. ℓ = 3 sin 15° B. ℓ = 3 cos 15° C. ℓ D. ℓ
 Over Lesson 12– 1 David needs a ramp that rises to a height of 3 feet at a 15° angle. Write an equation for the length ℓ of the ramp. A. ℓ = 3 sin 15° B. ℓ = 3 cos 15° C. ℓ D. ℓ
Over Lesson 12– 1 David needs a ramp that rises to a height of 3 feet at a 15° angle. Write an equation for the length ℓ of the ramp. A. ℓ = 3 sin 15° B. ℓ = 3 cos 15° C. ℓ D. ℓ
 Over Lesson 12– 1 At a construction site, the workers need to build a ramp up to the second story of a house. The angle of inclination of the ramp cannot be more than 20°. Find the length of the ramp if the distance to the second story is 15 feet. A. 5. 13 ft B. 15. 96 ft C. 41. 21 ft D. 43. 86 ft
Over Lesson 12– 1 At a construction site, the workers need to build a ramp up to the second story of a house. The angle of inclination of the ramp cannot be more than 20°. Find the length of the ramp if the distance to the second story is 15 feet. A. 5. 13 ft B. 15. 96 ft C. 41. 21 ft D. 43. 86 ft
 Over Lesson 12– 1 At a construction site, the workers need to build a ramp up to the second story of a house. The angle of inclination of the ramp cannot be more than 20°. Find the length of the ramp if the distance to the second story is 15 feet. A. 5. 13 ft B. 15. 96 ft C. 41. 21 ft D. 43. 86 ft
Over Lesson 12– 1 At a construction site, the workers need to build a ramp up to the second story of a house. The angle of inclination of the ramp cannot be more than 20°. Find the length of the ramp if the distance to the second story is 15 feet. A. 5. 13 ft B. 15. 96 ft C. 41. 21 ft D. 43. 86 ft
 Content Standards F. TF. 1 Understand radian measure of an angle as the length of the arc on the unit circle subtended by the angle. Mathematical Practices 2 Reason abstractly and quantitatively.
Content Standards F. TF. 1 Understand radian measure of an angle as the length of the arc on the unit circle subtended by the angle. Mathematical Practices 2 Reason abstractly and quantitatively.
 You used angles with degree measures. • Draw and find angles in standard position. • Convert between degree measures and radian measures.
You used angles with degree measures. • Draw and find angles in standard position. • Convert between degree measures and radian measures.
 • standard position • initial side • terminal side • coterminal angles • radian • central angle • arc length
• standard position • initial side • terminal side • coterminal angles • radian • central angle • arc length

 Draw an Angle in Standard Position A. Draw an angle with a measure of 210° in standard position. 210° = 180° + 30° Draw the terminal side of the angle 30° counterclockwise past the negative x-axis. Answer:
Draw an Angle in Standard Position A. Draw an angle with a measure of 210° in standard position. 210° = 180° + 30° Draw the terminal side of the angle 30° counterclockwise past the negative x-axis. Answer:
 Draw an Angle in Standard Position A. Draw an angle with a measure of 210° in standard position. 210° = 180° + 30° Draw the terminal side of the angle 30° counterclockwise past the negative x-axis. Answer:
Draw an Angle in Standard Position A. Draw an angle with a measure of 210° in standard position. 210° = 180° + 30° Draw the terminal side of the angle 30° counterclockwise past the negative x-axis. Answer:
 Draw an Angle in Standard Position B. Draw an angle with a measure of – 45° in standard position. The angle is negative. Draw the terminal side 45° clockwise from the positive x-axis. Answer:
Draw an Angle in Standard Position B. Draw an angle with a measure of – 45° in standard position. The angle is negative. Draw the terminal side 45° clockwise from the positive x-axis. Answer:
 Draw an Angle in Standard Position B. Draw an angle with a measure of – 45° in standard position. The angle is negative. Draw the terminal side 45° clockwise from the positive x-axis. Answer:
Draw an Angle in Standard Position B. Draw an angle with a measure of – 45° in standard position. The angle is negative. Draw the terminal side 45° clockwise from the positive x-axis. Answer:
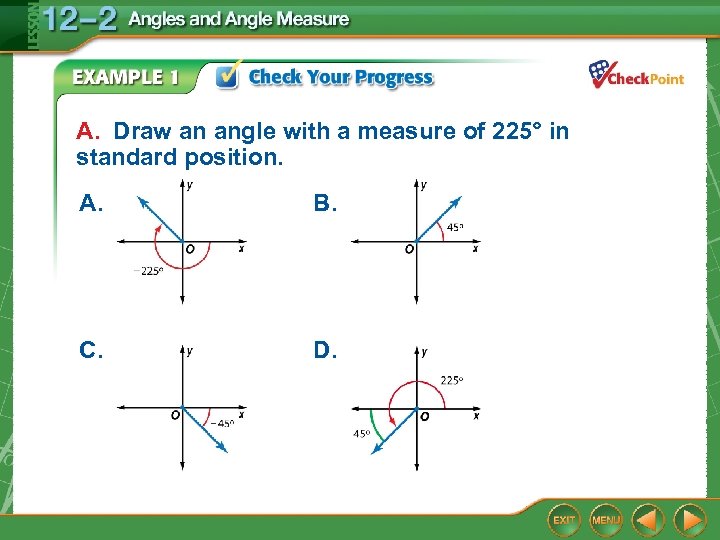 A. Draw an angle with a measure of 225° in standard position. A. B. C. D.
A. Draw an angle with a measure of 225° in standard position. A. B. C. D.
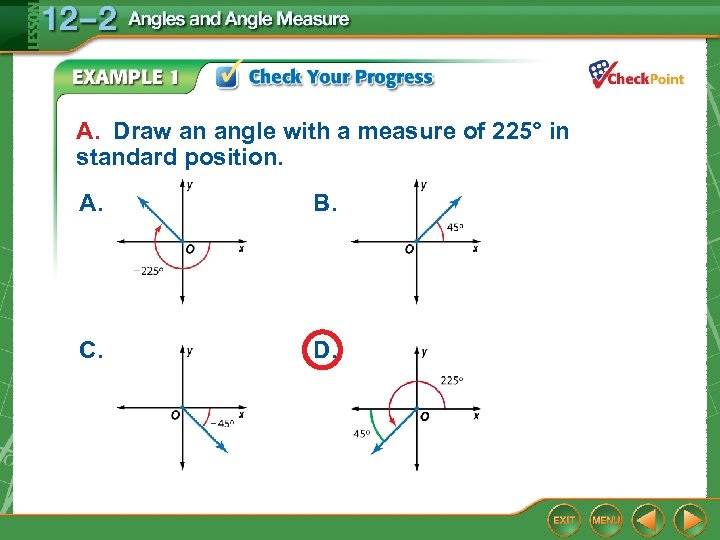 A. Draw an angle with a measure of 225° in standard position. A. B. C. D.
A. Draw an angle with a measure of 225° in standard position. A. B. C. D.
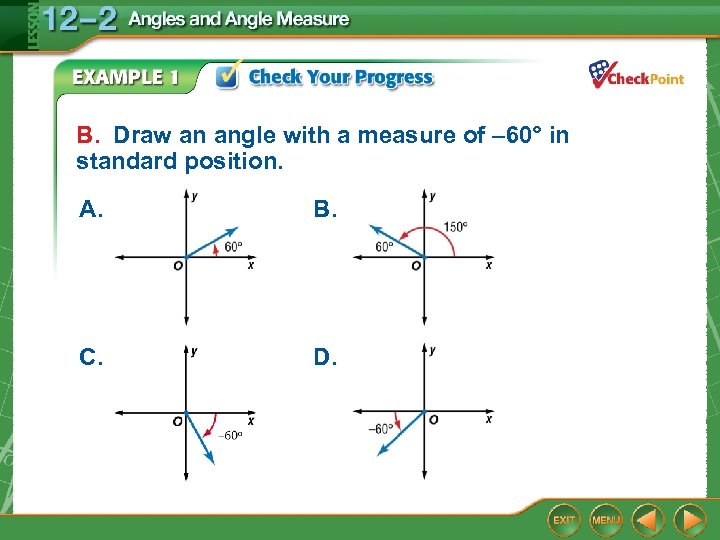 B. Draw an angle with a measure of – 60° in standard position. A. B. C. D.
B. Draw an angle with a measure of – 60° in standard position. A. B. C. D.
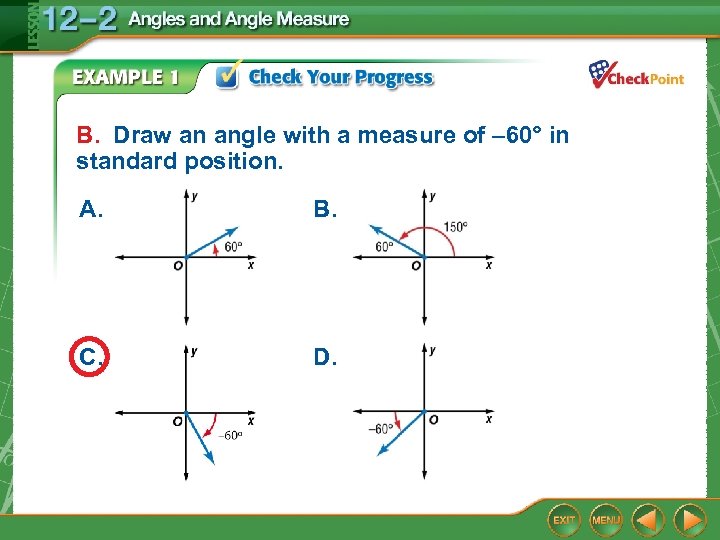 B. Draw an angle with a measure of – 60° in standard position. A. B. C. D.
B. Draw an angle with a measure of – 60° in standard position. A. B. C. D.
 Draw an Angle in Standard Position A. DIVING In a springboard diving competition, a diver made a 900 -degree rotation before slicing into the water. Draw an angle in standard position that measures 900° = 360° + 180° Draw the terminal side of the angle 180° past the positive x-axis. Answer:
Draw an Angle in Standard Position A. DIVING In a springboard diving competition, a diver made a 900 -degree rotation before slicing into the water. Draw an angle in standard position that measures 900° = 360° + 180° Draw the terminal side of the angle 180° past the positive x-axis. Answer:
 Draw an Angle in Standard Position A. DIVING In a springboard diving competition, a diver made a 900 -degree rotation before slicing into the water. Draw an angle in standard position that measures 900° = 360° + 180° Draw the terminal side of the angle 180° past the positive x-axis. Answer:
Draw an Angle in Standard Position A. DIVING In a springboard diving competition, a diver made a 900 -degree rotation before slicing into the water. Draw an angle in standard position that measures 900° = 360° + 180° Draw the terminal side of the angle 180° past the positive x-axis. Answer:
 SNOWBOARDING While riding down the mountain, a snowboarder goes off a jump and turns 600° before touching down onto the snow again. Determine how many degrees past the positive x-axis the snowboarder lands. A. 120° B. 180° C. 240° D. 300°
SNOWBOARDING While riding down the mountain, a snowboarder goes off a jump and turns 600° before touching down onto the snow again. Determine how many degrees past the positive x-axis the snowboarder lands. A. 120° B. 180° C. 240° D. 300°
 SNOWBOARDING While riding down the mountain, a snowboarder goes off a jump and turns 600° before touching down onto the snow again. Determine how many degrees past the positive x-axis the snowboarder lands. A. 120° B. 180° C. 240° D. 300°
SNOWBOARDING While riding down the mountain, a snowboarder goes off a jump and turns 600° before touching down onto the snow again. Determine how many degrees past the positive x-axis the snowboarder lands. A. 120° B. 180° C. 240° D. 300°
 Find Coterminal Angles A. Find an angle with a positive measure and an angle with a negative measure that are coterminal with 210°. positive angle: 210° + 360° = 570° negative angle: 210° – 360° = – 150° Answer:
Find Coterminal Angles A. Find an angle with a positive measure and an angle with a negative measure that are coterminal with 210°. positive angle: 210° + 360° = 570° negative angle: 210° – 360° = – 150° Answer:
 Find Coterminal Angles A. Find an angle with a positive measure and an angle with a negative measure that are coterminal with 210°. positive angle: 210° + 360° = 570° negative angle: 210° – 360° = – 150° Answer: 570° and – 150°
Find Coterminal Angles A. Find an angle with a positive measure and an angle with a negative measure that are coterminal with 210°. positive angle: 210° + 360° = 570° negative angle: 210° – 360° = – 150° Answer: 570° and – 150°
 Find Coterminal Angles B. Find an angle with a positive measure and an angle with a negative measure that are coterminal with – 120°. positive angle: 120° + 360° = 240° negative angle: 120° – 360° = – 480° Answer:
Find Coterminal Angles B. Find an angle with a positive measure and an angle with a negative measure that are coterminal with – 120°. positive angle: 120° + 360° = 240° negative angle: 120° – 360° = – 480° Answer:
 Find Coterminal Angles B. Find an angle with a positive measure and an angle with a negative measure that are coterminal with – 120°. positive angle: 120° + 360° = 240° negative angle: 120° – 360° = – 480° Answer: 240° and – 480°
Find Coterminal Angles B. Find an angle with a positive measure and an angle with a negative measure that are coterminal with – 120°. positive angle: 120° + 360° = 240° negative angle: 120° – 360° = – 480° Answer: 240° and – 480°
 A. Find an angle with a positive measure and an angle with a negative measure that are coterminal with 330°. A. – 30°, 690° B. – 30°, 630° C. – 60°, 630° D. – 60°, 720°
A. Find an angle with a positive measure and an angle with a negative measure that are coterminal with 330°. A. – 30°, 690° B. – 30°, 630° C. – 60°, 630° D. – 60°, 720°
 A. Find an angle with a positive measure and an angle with a negative measure that are coterminal with 330°. A. – 30°, 690° B. – 30°, 630° C. – 60°, 630° D. – 60°, 720°
A. Find an angle with a positive measure and an angle with a negative measure that are coterminal with 330°. A. – 30°, 690° B. – 30°, 630° C. – 60°, 630° D. – 60°, 720°
 B. Find an angle with a positive measure and an angle with a negative measure that are coterminal with – 80°. A. – 380°, 220° B. – 440°, 280° C. – 320°, 380° D. – 400°, 300°
B. Find an angle with a positive measure and an angle with a negative measure that are coterminal with – 80°. A. – 380°, 220° B. – 440°, 280° C. – 320°, 380° D. – 400°, 300°
 B. Find an angle with a positive measure and an angle with a negative measure that are coterminal with – 80°. A. – 380°, 220° B. – 440°, 280° C. – 320°, 380° D. – 400°, 300°
B. Find an angle with a positive measure and an angle with a negative measure that are coterminal with – 80°. A. – 380°, 220° B. – 440°, 280° C. – 320°, 380° D. – 400°, 300°

 Convert Between Degrees and Radians A. Rewrite 30° in radians. Answer:
Convert Between Degrees and Radians A. Rewrite 30° in radians. Answer:
 Convert Between Degrees and Radians A. Rewrite 30° in radians. Answer:
Convert Between Degrees and Radians A. Rewrite 30° in radians. Answer:
 Convert Between Degrees and Radians B. Rewrite Answer: in degrees.
Convert Between Degrees and Radians B. Rewrite Answer: in degrees.
 Convert Between Degrees and Radians B. Rewrite Answer: – 300° in degrees.
Convert Between Degrees and Radians B. Rewrite Answer: – 300° in degrees.
 A. Rewrite 45° in radians. A. B. C. D.
A. Rewrite 45° in radians. A. B. C. D.
 A. Rewrite 45° in radians. A. B. C. D.
A. Rewrite 45° in radians. A. B. C. D.
 B. Rewrite A. 70° B. 80° C. 30° D. 60° in degrees.
B. Rewrite A. 70° B. 80° C. 30° D. 60° in degrees.
 B. Rewrite A. 70° B. 80° C. 30° D. 60° in degrees.
B. Rewrite A. 70° B. 80° C. 30° D. 60° in degrees.


 Find Arc Length TRUCKS The steering wheel on a monster truck has a radius of 11 inches. How far does a point on the steering wheel travel if the wheel makes four fifths of a rotation? Step 1 Find the central angle in radians.
Find Arc Length TRUCKS The steering wheel on a monster truck has a radius of 11 inches. How far does a point on the steering wheel travel if the wheel makes four fifths of a rotation? Step 1 Find the central angle in radians.
 Find Arc Length Step 2 s = r ≈ 55. 3 in. Answer: Use the radius and the central angle to find the arc length. Write the formula for arc length. Use a calculator to simplify.
Find Arc Length Step 2 s = r ≈ 55. 3 in. Answer: Use the radius and the central angle to find the arc length. Write the formula for arc length. Use a calculator to simplify.
 Find Arc Length Step 2 s = r ≈ 55. 3 in. Use the radius and the central angle to find the arc length. Write the formula for arc length. Use a calculator to simplify. Answer: A point on the steering wheel will travel about 55. 3 inches after four fifths of a rotation.
Find Arc Length Step 2 s = r ≈ 55. 3 in. Use the radius and the central angle to find the arc length. Write the formula for arc length. Use a calculator to simplify. Answer: A point on the steering wheel will travel about 55. 3 inches after four fifths of a rotation.
 BOATS The steering wheel on a yacht has a radius of 16 inches. How far does a point on the steering wheel travel if the wheel makes five sevenths of a rotation? A. 61. 1 in. B. 64. 6 in. C. 71. 8 in. D. 74. 9 in.
BOATS The steering wheel on a yacht has a radius of 16 inches. How far does a point on the steering wheel travel if the wheel makes five sevenths of a rotation? A. 61. 1 in. B. 64. 6 in. C. 71. 8 in. D. 74. 9 in.
 BOATS The steering wheel on a yacht has a radius of 16 inches. How far does a point on the steering wheel travel if the wheel makes five sevenths of a rotation? A. 61. 1 in. B. 64. 6 in. C. 71. 8 in. D. 74. 9 in.
BOATS The steering wheel on a yacht has a radius of 16 inches. How far does a point on the steering wheel travel if the wheel makes five sevenths of a rotation? A. 61. 1 in. B. 64. 6 in. C. 71. 8 in. D. 74. 9 in.

