Finite State Verification An Emerging Technology for Validating

Finite State Verification: An Emerging Technology for Validating Software Systems Lori A. Clarke University of Massachusetts Clarke@cs. umass. edu http: //laser. cs. umass. edu/ UMASS Laboratory for Advanced Software Engineering Research

Outline of Presentation • Lay of the Land: – Testing, Theorem-proving based verification, Finite state verification(FSV) • Overview of FSV • Look at 3 Different Approaches to FSV – Model Checking – Flow Equations – Data Flow Analysis • Major Challenges to be Addressed UMASS Laboratory for Advanced Software Engineering Research

Sorry State of Affairs • Testing consumes about half the cost of s/w development • Maintenance consumes about 80% of the full life cycle costs--much of that devoted to testing • Most companies use ad hoc QA practices • Unhappy with the results; Unhappy with the cost – Failed projects – Delayed product releases UMASS Laboratory for Advanced Software Engineering Research

Testing • can: – Uncover failures – Show specifications are (not) met for specific test cases – Be an indication of overall reliability • cannot: – Prove that a program will/will not behave in a particular way UMASS Laboratory for Advanced Software Engineering Research

Must do better! • Increasing number of high assurance applications – Medical applications – Flight control software – Electronic commerce • Increasing number of complex systems – Systems of systems – Distributed systems UMASS Laboratory for Advanced Software Engineering Research

Distributed Systems • Better performance, better flexibility, but there is a cost • distributed systems are more difficult to test than sequential systems – number of execution paths can grow exponentially with the number of processes – Testing can not even demonstrate that a system works on the selected/executed test data UMASS Laboratory for Advanced Software Engineering Research

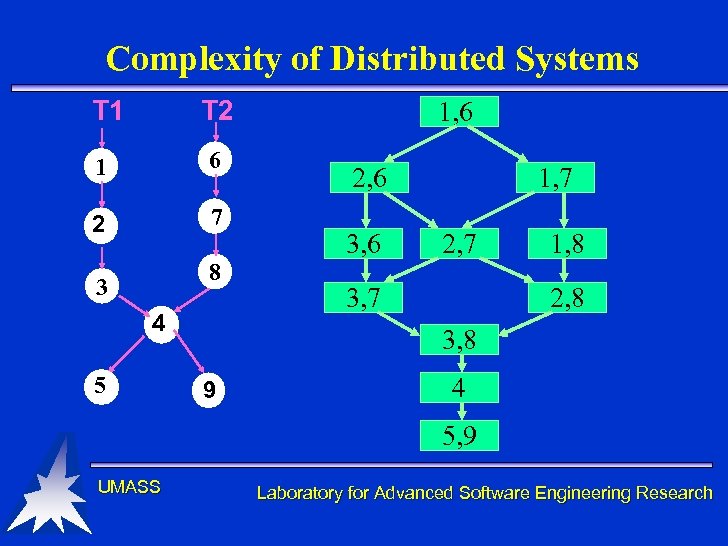Complexity of Distributed Systems T 1 T 2 1 6 2 7 8 3 4 5 1, 6 2, 6 3, 6 1, 7 2, 7 3, 7 1, 8 2, 8 3, 8 9 4 5, 9 UMASS Laboratory for Advanced Software Engineering Research

Uncertainty of Testing T 1 1 6 2 X: =1 T 2 7 1, 6 2, 6 X: =2 8 3 2, 7 3, 7 4 5 3, 6 1, 7 1, 8 2, 8 3, 8 9 X==? 4 5, 9 UMASS Laboratory for Advanced Software Engineering Research

Formal Verification: An Alternative to Testing • Theorem Proving Based Verification – Use mathematical reasoning – Prove properties about all possible executions – Difficult and error prone • Finite State Verification – Reason about a finite model of the system – Prove properties about all possible executions, but not as powerful as theorem proving – Almost a totally automated process UMASS Laboratory for Advanced Software Engineering Research

Spectrum of Difficulty Systematic Testing Ad-hoc Testing • Arbitrary testcases • Reqts based test planning UMASS Finite State Verification Theorem Proving • Requirements captured as properties • Properties guaranteed on all possible executions Laboratory for Advanced Software Engineering Research

Finite State Verification (FSV) • Holds the promise of providing a cost effective way of verifying important properties about a system – Not all faults are created equal – Invest effort into most important properties • Several promising prototypes – Reachability Based • SPIN or Symbolic Model Checking (SMV) – Flow Equations • Integer Necessary Conditions (INCA) – Data Flow Analysis • FLAVERS UMASS Laboratory for Advanced Software Engineering Research

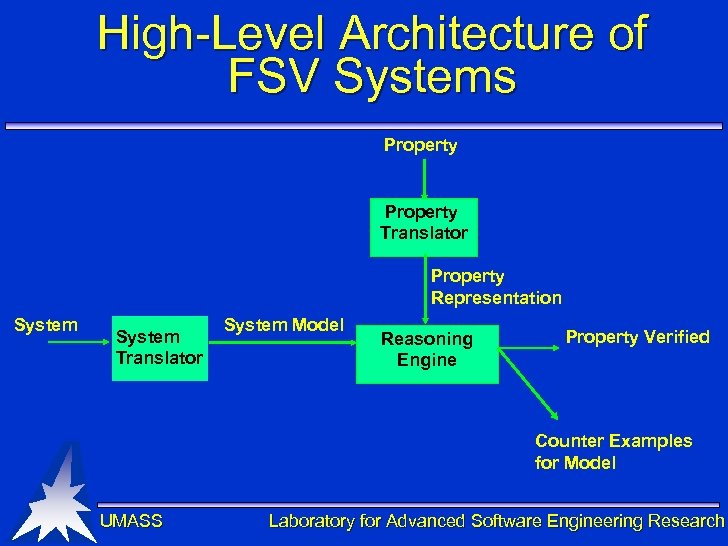High-Level Architecture of FSV Systems Property Translator Property Representation System Translator System Model Reasoning Engine Property Verified Counter Examples for Model UMASS Laboratory for Advanced Software Engineering Research

Conservative Analysis • If property verified, property holds for all possible executions of the system • If property not verified: – An error OR – A spurious result • System model abstracts information to be tractable • Conservative abstractions over-approximate behavior • If inconsistency relies upon over-approximations, then a spurious result – e. g. counter example corresponds to an infeasible path UMASS Laboratory for Advanced Software Engineering Research

System Model • Depends on property being verified • Eliminate information that does not impact the proof • Abstraction techniques allows “states” in the model to be reduced/collapsed UMASS Laboratory for Advanced Software Engineering Research

Some Properties of Properties • State-based versus event-based • Once temperature is greater than 100 degrees, lock is true • Elevator door closes before elevator moves • Single locations versus (sub)paths – Deadlock or race conditions – Sequences of states or events • Safety versus Liveness UMASS Laboratory for Advanced Software Engineering Research

A quick look at three approaches to FSV • Model Checking • Flow Equations • Data Flow Analysis Big Disclaimer! UMASS Laboratory for Advanced Software Engineering Research

Model Checking: some history • Originally proposed for hardware • Early 80’s: E. Clarke and Emerson; Quielle and Sifakis • Late 80’s: Improved algorithms and property notations (E. Clarke, Emerson, Sistla) • 90’s: Symbolic Model Checking (SMV) and other optimizations (Burch, E. Clarke, Dill, Long, and Mc. Millan) • Current: Hybrid approaches UMASS Laboratory for Advanced Software Engineering Research

Model Checking • Properties usually expressed in a temporal logic • System represented as a (possibly “abstracted”) reachability graph – State based • Reasoning engine propagates valid subformulas through the graph UMASS Laboratory for Advanced Software Engineering Research

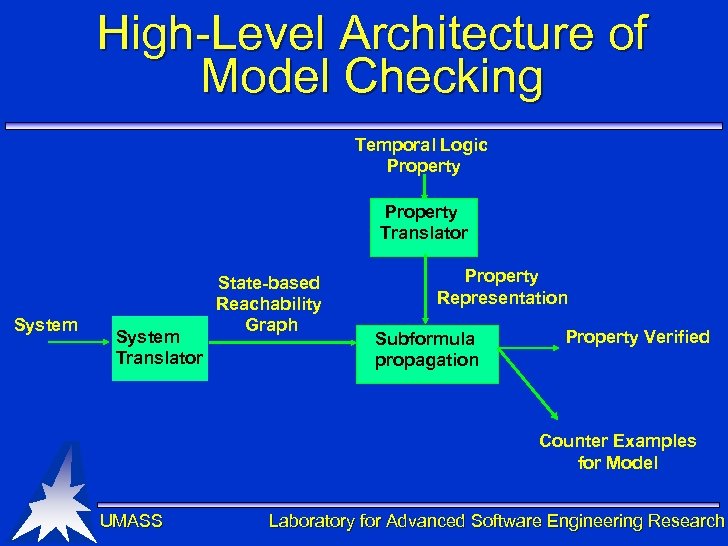High-Level Architecture of Model Checking Temporal Logic Property Translator System Translator State-based Reachability Graph Property Representation Subformula propagation Property Verified Counter Examples for Model UMASS Laboratory for Advanced Software Engineering Research

Representing Properties • CTL operators – G - globally – F - future – X- next – U - until • At a state in the model: – AG p means that for all paths from this state, p is true and will remain true – EF p means that for some path from this state, p will eventually be true UMASS Laboratory for Advanced Software Engineering Research

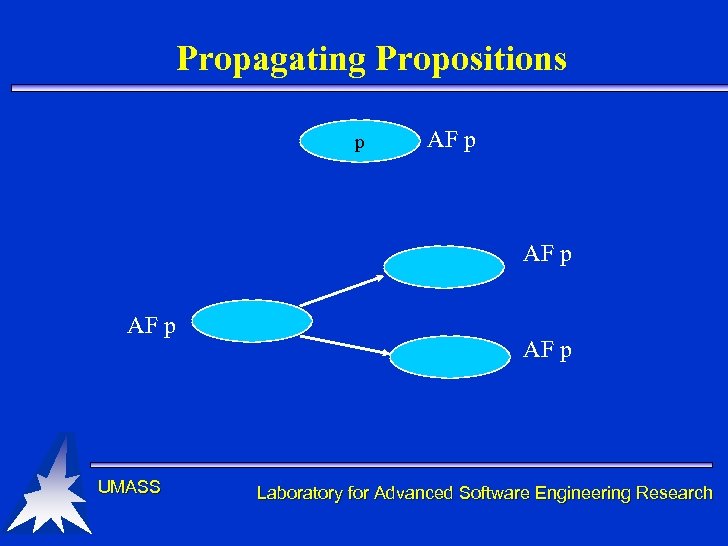Propagating Propositions p AF p UMASS AF p Laboratory for Advanced Software Engineering Research

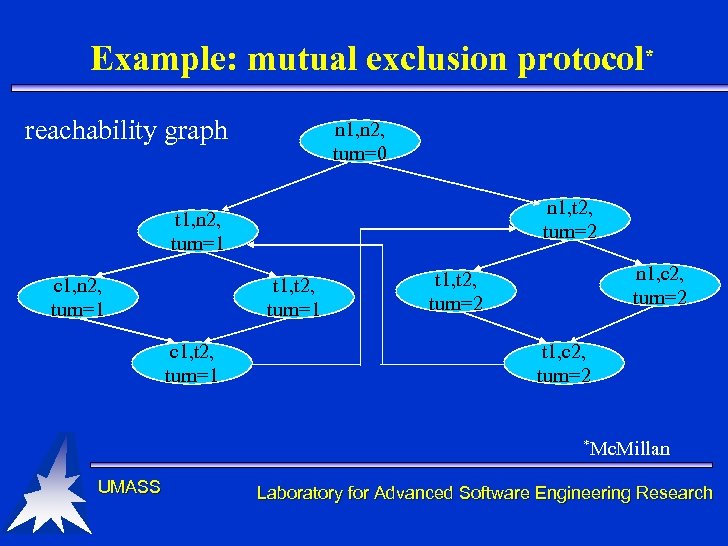Example: mutual exclusion protocol* reachability graph n 1, n 2, turn=0 n 1, t 2, turn=2 t 1, n 2, turn=1 c 1, n 2, turn=1 t 1, t 2, turn=1 c 1, t 2, turn=1 n 1, c 2, turn=2 t 1, t 2, turn=2 t 1, c 2, turn=2 *Mc. Millan UMASS Laboratory for Advanced Software Engineering Research

Example Property • AG(t 1=>AF c 1) • If process 1 tries (t 1) to get the lock then eventually it gets into its critical region (c 1) • Note, would like to prove this for all processes but FSV approaches usually must instantiate property (and system) UMASS Laboratory for Advanced Software Engineering Research

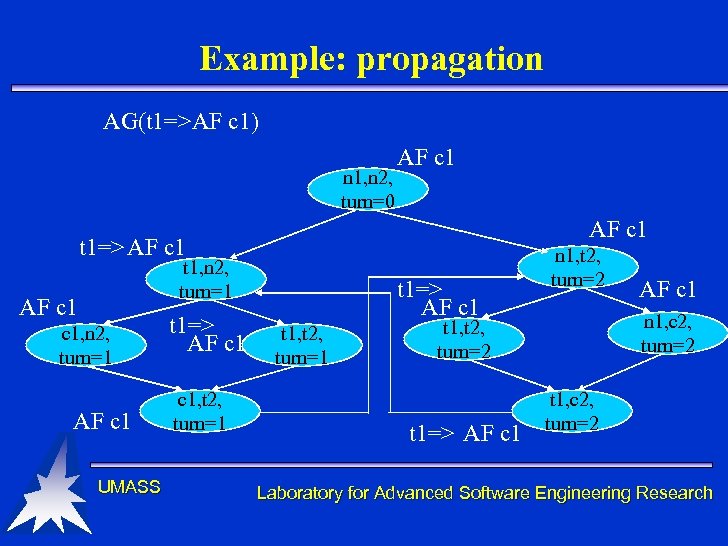Example: propagation AG(t 1=>AF c 1) n 1, n 2, turn=0 AF c 1 t 1=> AF c 1 t 1, n 2, turn=1 AF c 1 UMASS t 1=> AF c 1, t 2, turn=1 t 1=> AF c 1 t 1, t 2, turn=1 n 1, t 2, turn=2 n 1, c 2, turn=2 t 1, t 2, turn=2 t 1=> AF c 1 t 1, c 2, turn=2 Laboratory for Advanced Software Engineering Research

Formula Propagation • Propagate until no change – propagate from smaller to larger subformulas – “smart” algorithm: linear in the size of model and size of the formula • Many optimization techniques – Symbolic model checking – Use efficient algorithms that propagate subformula for sets of values UMASS Laboratory for Advanced Software Engineering Research

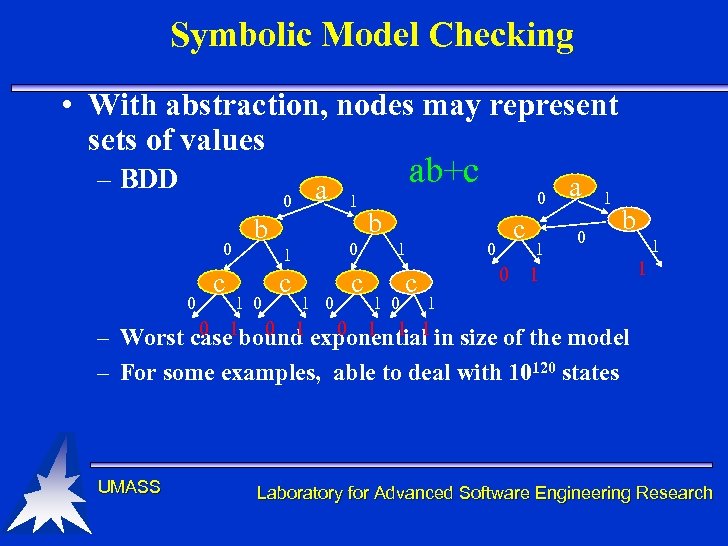Symbolic Model Checking • With abstraction, nodes may represent sets of values – BDD 0 0 0 c a b ab+c 1 1 1 0 0 c c 1 0 0 b 1 1 0 c c 0 0 1 a 0 1 b 1 1 0 0 1 1 1 – Worst case 1 bound exponential in size of the model – For some examples, able to deal with 10120 states UMASS Laboratory for Advanced Software Engineering Research

Some observations: Model Checking • Worst case bound linear in size of the model – Model exponential • Experimentally often very effective • Not clear if model checking or symbolic model checking is superior – Depends on the problem UMASS Laboratory for Advanced Software Engineering Research

Flow Equations: some history • Originally proposed for designs • Early 80’s: Initial development (Avrunin, Dillon, and Wileden) • 90’s: Optimized and extended to real-time (Avrunin, Buy, Corbett, Dillon, and Wileden) • Current: INCA prototype (Avrunin, Corbett, and Siegel) UMASS Laboratory for Advanced Software Engineering Research

Flow Equations • Model system as finite state automata • Use extended network flow inequalities to capture legal flow through a concurrent system • Represent negation of the property as a set of inequalities UMASS Laboratory for Advanced Software Engineering Research

Solving the Set of Inequalities • Determine if combined system of inequalities is consistent – Use integer linear programming • If consistent, there is a set of flows through automata that violate the property • Provides guidance for trace through the model (but may not be executable) UMASS Laboratory for Advanced Software Engineering Research

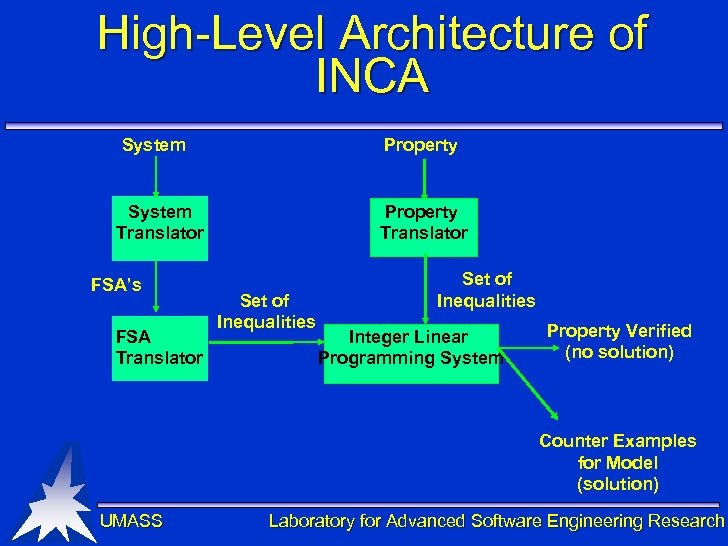High-Level Architecture of INCA System Property Translator System Translator FSA’s FSA Translator Set of Inequalities Integer Linear Programming System Property Verified (no solution) Counter Examples for Model (solution) UMASS Laboratory for Advanced Software Engineering Research

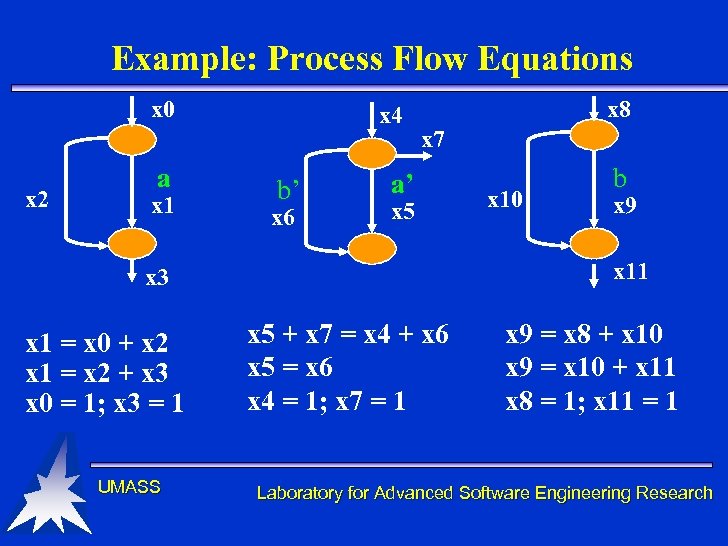Example: Process Flow Equations x 0 x 2 a x 1 x 4 b’ x 6 x 8 x 7 a’ x 5 UMASS x 9 x 11 x 3 x 1 = x 0 + x 2 x 1 = x 2 + x 3 x 0 = 1; x 3 = 1 x 10 b x 5 + x 7 = x 4 + x 6 x 5 = x 6 x 4 = 1; x 7 = 1 x 9 = x 8 + x 10 x 9 = x 10 + x 11 x 8 = 1; x 11 = 1 Laboratory for Advanced Software Engineering Research

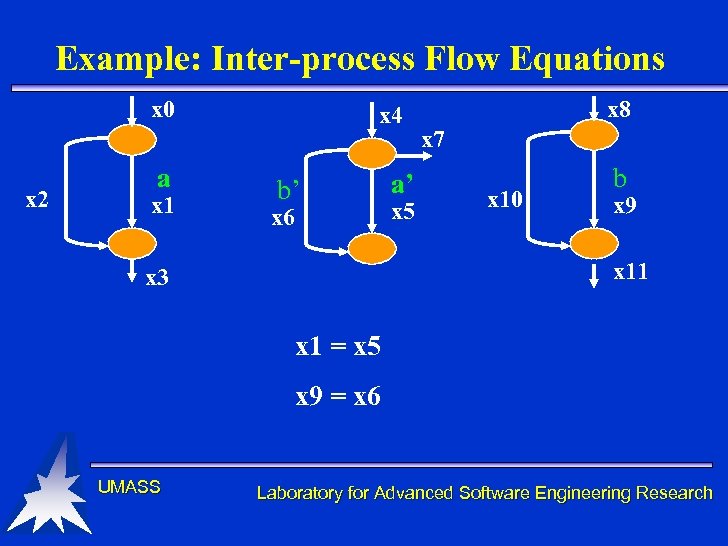Example: Inter-process Flow Equations x 0 x 2 a x 1 x 4 b’ x 6 a’ x 5 x 8 x 7 x 10 b x 9 x 11 x 3 x 1 = x 5 x 9 = x 6 UMASS Laboratory for Advanced Software Engineering Research

Solving for a property x 1 = x 0 + x 2 x 1 = x 2 + x 3 x 0 = 1; x 3 = 1 x 5 + x 7 = x 4 + x 6 x 5 = x 6 x 4 = 1; x 7 = 1 x 9 = x 8 + x 10 x 9 = x 10 + x 11 x 8 = 1; x 11=1 x 1 = x 5 x 9 =x 6 j: 0 ≤ xj UMASS Property: For all paths, event a occurs more than event b represent complement ¬(x 1 > x 9) = = (x 1 ≤ x 9) Solution exists e. g. , x 2, x 10 = 0, all other xi = 1 => property does not hold Laboratory for Advanced Software Engineering Research

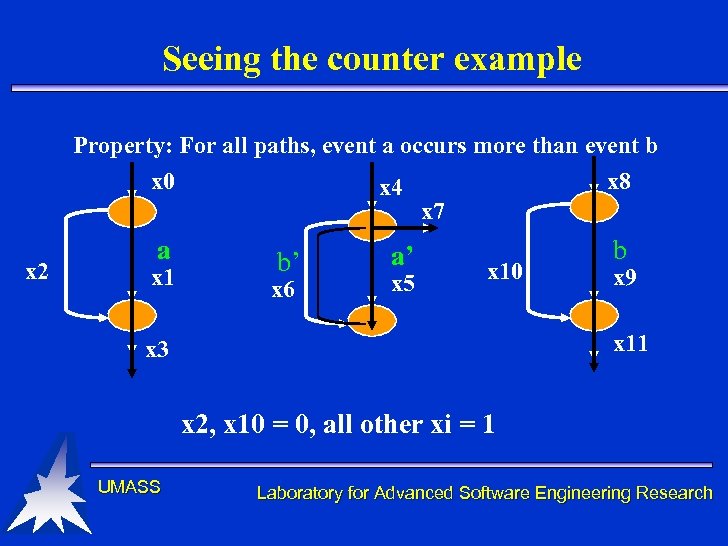Seeing the counter example Property: For all paths, event a occurs more than event b x 0 x 8 x 4 x 7 x 2 a x 1 b’ x 6 a’ x 5 x 10 b x 9 x 11 x 3 x 2, x 10 = 0, all other xi = 1 UMASS Laboratory for Advanced Software Engineering Research

Some Limitations • Integer Linear Programming has an exponential worst case bound • Inter-process order information is not preserved – only checks whether event counts are consistent – Like most static techniques, may produce spurious results UMASS Laboratory for Advanced Software Engineering Research

Some Benefits • Does not enumerate the state space! • Integer linear Programming is often very efficient – Empirical evidence: linear inequality systems usually grow linearly and take sub-exponential times to solve • In practice, INCA is usually an effective technique UMASS Laboratory for Advanced Software Engineering Research

Data Flow Based Verification: some history • Mid-70’s: Originally proposed for def-ref anomalies in FORTRAN (Osterweil and Fosdick) • Early 80’s: Extended to general properties (Olender and Osterweil) & concurrency (Taylor and Osterweil) • 90’s: Deadlock detection (Masticola and Ryder); Efficient representation of concurrency & incremental precision improvement (Dwyer and L. Clarke) • Recent: Optimizations, Java (Avrunin, L. Clarke, Cobleigh, Naumovich, and Osterweil) UMASS Laboratory for Advanced Software Engineering Research

Data Flow Analysis: FLAVERS • Represents property as a finite state automaton • System model is collection of annotated control flow graphs – Inter-process communication and interleavings are represented with additional edges – does not enumerate all reachable states – over-approximates relevant executable behaviors • Reasoning engine based on data flow analysis UMASS Laboratory for Advanced Software Engineering Research

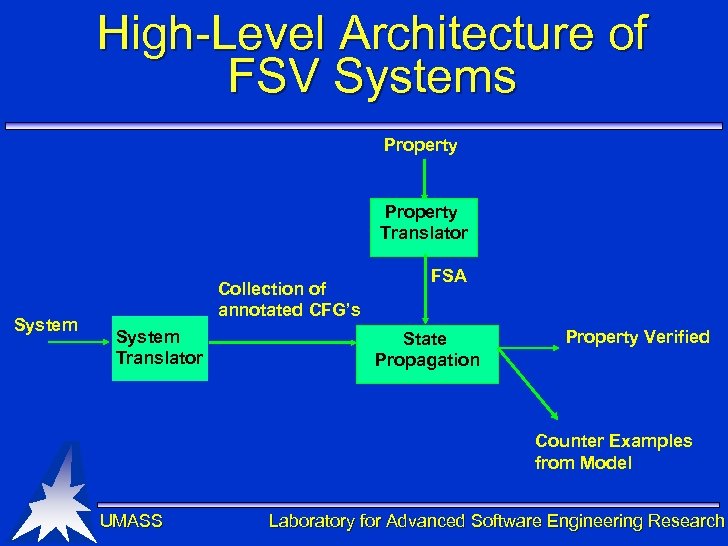High-Level Architecture of FSV Systems Property Translator System Collection of annotated CFG’s System Translator FSA State Propagation Property Verified Counter Examples from Model UMASS Laboratory for Advanced Software Engineering Research

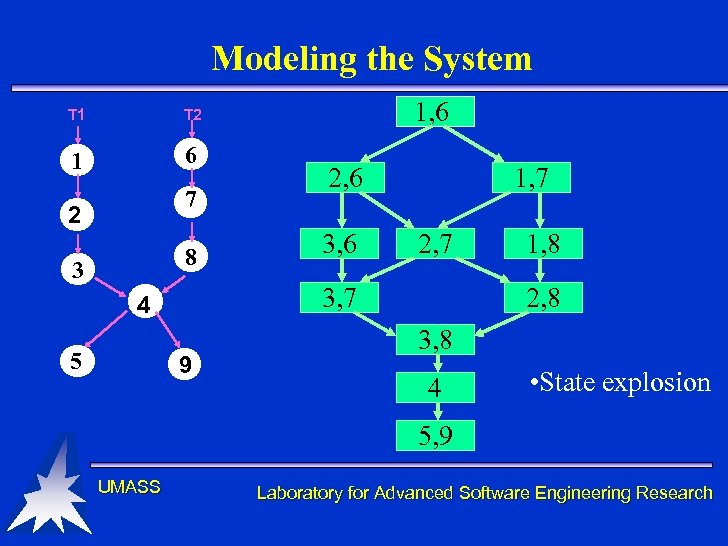Modeling the System T 1 1 6 1, 6 T 2 7 2 8 3 3, 6 1, 7 2, 7 3, 7 4 5 2, 6 9 1, 8 2, 8 3, 8 4 • State explosion 5, 9 UMASS Laboratory for Advanced Software Engineering Research

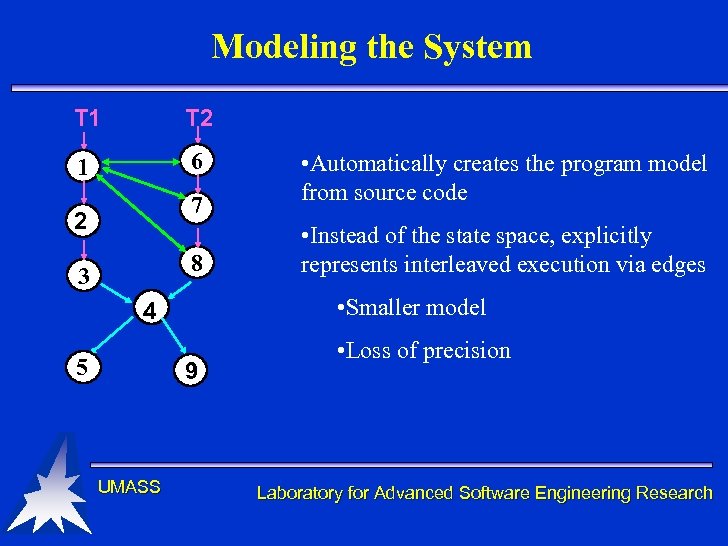Modeling the System T 1 T 2 1 6 7 2 8 3 9 UMASS • Instead of the state space, explicitly represents interleaved execution via edges • Smaller model 4 5 • Automatically creates the program model from source code • Loss of precision Laboratory for Advanced Software Engineering Research

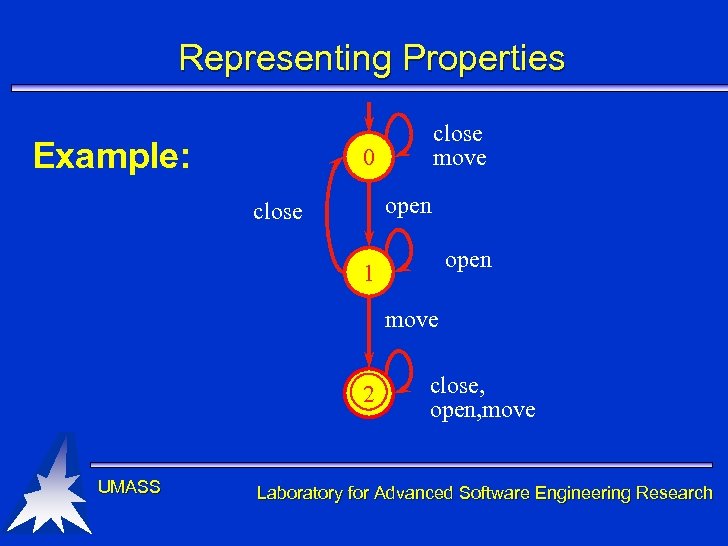Representing Properties Example: close move 0 open close open 1 move 2 UMASS close, open, move Laboratory for Advanced Software Engineering Research

State Propagation • States of the property are propagated through the model • The property is proved if only accepting (non-accepting) states are contained in the final node of the model UMASS Laboratory for Advanced Software Engineering Research

Example public static void main (String [] args) { … if (elevator. Stopped) {. . . open. Doors(); } record. State(); if (elevator. Stopped) {. . . close. Doors(); } move. To. Next. Floor(); } UMASS if open if close move Laboratory for Advanced Software Engineering Research

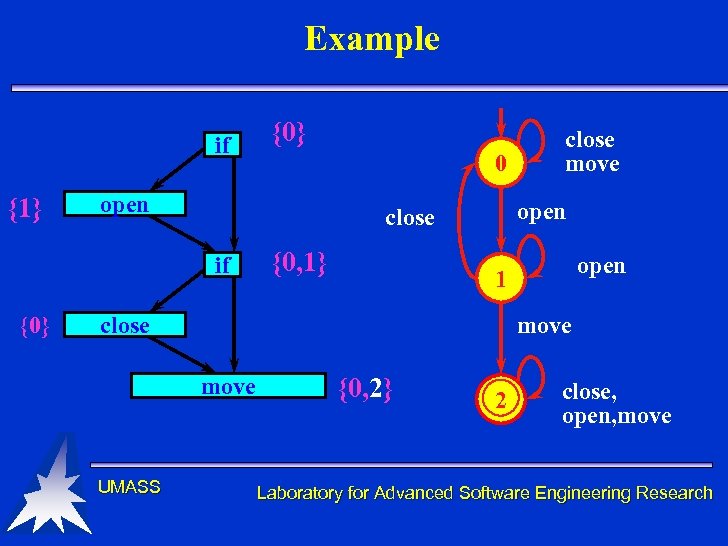Example if {1} 0 open {0, 1} open 1 move close move UMASS close move open close if {0} {0, 2} 2 close, open, move Laboratory for Advanced Software Engineering Research

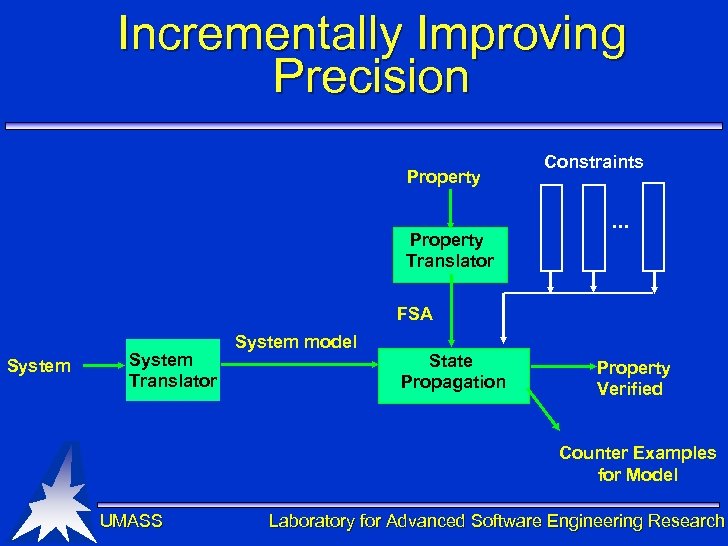Incrementally Improving Precision Property Translator Constraints . . . FSA System Translator System model State Propagation Property Verified Counter Examples for Model UMASS Laboratory for Advanced Software Engineering Research

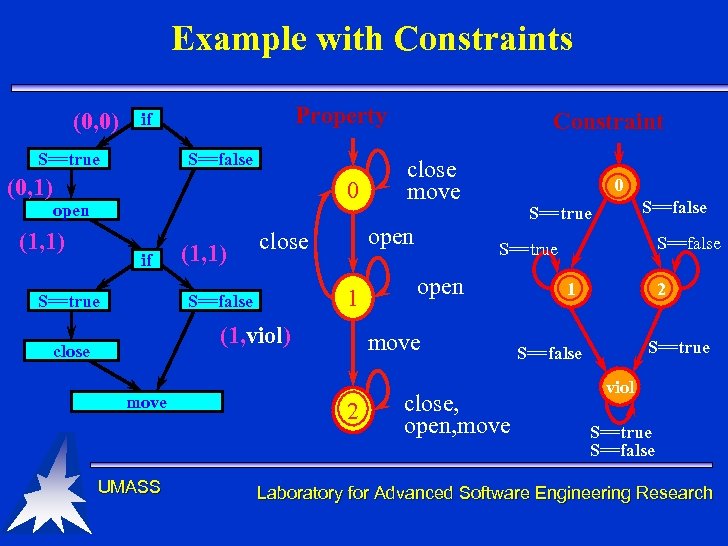Example with Constraints (0, 0) Property if S==true S==false (0, 1) 0 open (1, 1) if S==true (1, 1) 1 (1, viol) close move UMASS close move open close S==false Constraint 0 S==false S==true open move 2 S==false S==true close, open, move 1 2 S==true S==false viol S==true S==false Laboratory for Advanced Software Engineering Research

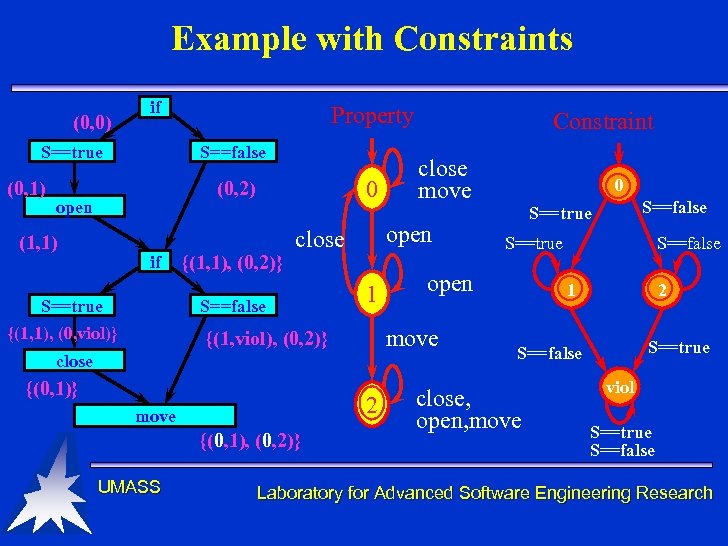Example with Constraints (0, 0) if S==true (0, 1) Property S==false 0 (0, 2) open (1, 1) if S==true {(1, 1), (0, 2)} {(1, 1), (0, viol)} 1 close 2 move {(0, 1), (0, 2)} UMASS 0 S==false S==true open move {(1, viol), (0, 2)} {(0, 1)} close move open close S==false Constraint S==false 1 2 S==true S==false close, open, move viol S==true S==false Laboratory for Advanced Software Engineering Research

Some Observations: Data Flow Analysis • Overall complexity is O(N 2 S) – N is the # nodes in the model – S is the number of states: property x constraints – Experimentally: performance subexponential • Usually requires several iterations to determine needed constraints • Constraints – Many automatically generated on request – Can be used to model other information UMASS Laboratory for Advanced Software Engineering Research

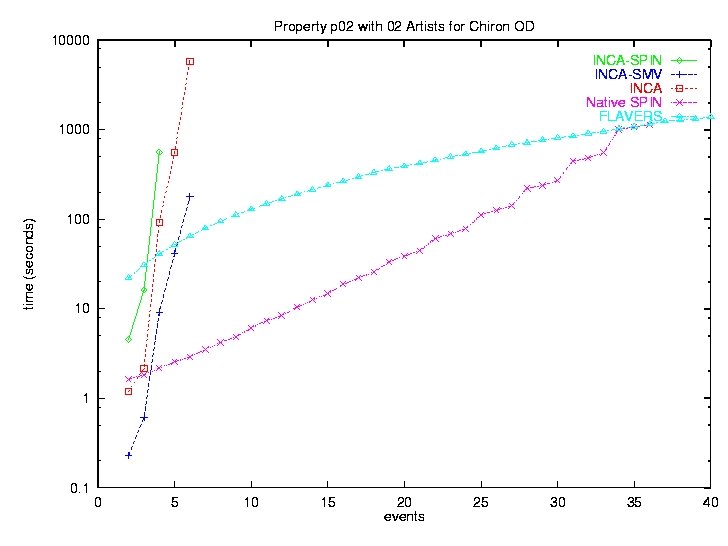
Experimental Comparisons • All these approaches are: – very effective on some problems – disappointing on some problems • Hard to predict how they will perform • Experimental results – George S. Avrunin, James C. Corbett, Matthew B. Dwyer, Corina S. Pasareanu, and Stephen F. Siegel, Comparing Finite-State Verification Techniques for Concurrent Software Very Big Disclaimer! UMASS Laboratory for Advanced Software Engineering Research

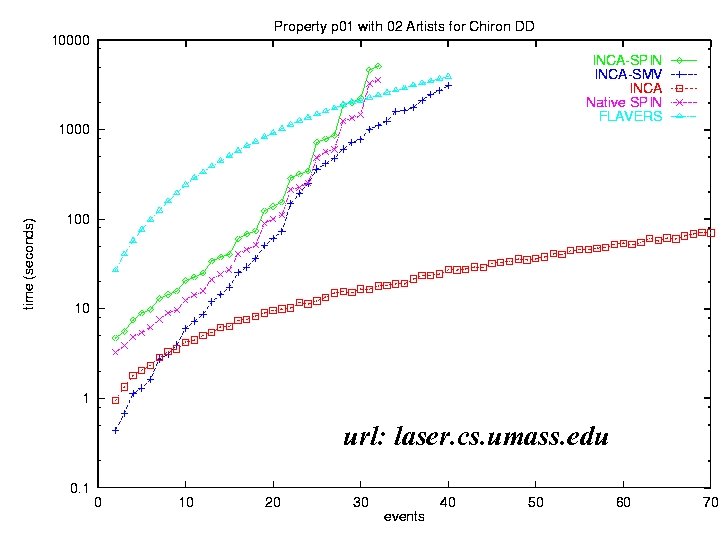url: laser. cs. umass. edu UMASS Laboratory for Advanced Software Engineering Research

Can we move beyond academic prototypes to practitioners’ tools? • Yes, but there is more work to be done – – Optimization, optimization Process support Better support for specifying properties Better support for generating, selecting, visualizing counter example traces – Better approaches for dealing with dynamism – Full support for real languages – Full lifecycle support • Integration with testing UMASS Laboratory for Advanced Software Engineering Research

Specifying Properties • It is very hard to specify properties precisely – E. g. , open and close file repeatedly • Must file always be opened? Or, IF it is opened, then it must be closed? • Can file be opened repeatedly before it is closed? • Need notations that are easy to use – Specification patterns • Need tools to help understand properties – need to test the properties UMASS Laboratory for Advanced Software Engineering Research

Counter Example Traces • Want “short” but “useful” counter examples • How to select the “next” counter example? • How to incorporate user guidance? • How to go from traces in the model to traces in the program? UMASS Laboratory for Advanced Software Engineering Research

Dynamism • FSV is a static analysis approach that deals with static models – Must create a specific instance of the model • E. g. , N philosophers => 5 philosphers – Can not handle • dynamic objects • dynamic process creation • Need hybrid techniques that integrate theorem proving with FSV UMASS Laboratory for Advanced Software Engineering Research

Support for Real Languages • Many language features have not been addressed – Aliasing – Exception handling – Event based notification UMASS Laboratory for Advanced Software Engineering Research

Lifecycle-based Verification • High-level architectural design – Extremely important for distributed systems • Detect problems early – Need to support heterogeneous interaction models • Low-level design – Additional detail leads to additional properties – Need to maintain consistency with the HLA UMASS Laboratory for Advanced Software Engineering Research

Lifecycle-based Verification (continued) • Coding – Partial systems – Incremental, compositional development/verification • Debugging – Hypothesize fault in terms of a property – FSV provides a counter example trace or invalidates hypothesis UMASS Laboratory for Advanced Software Engineering Research

Lifecycle-based verification (continued) • Testing – Generalize test cases to their corresponding property – Test planning via requirements based property specification • Regression testing – re-verify properties that should not have changed • Need efficient re-verification techniques UMASS Laboratory for Advanced Software Engineering Research

Integrating Testing and Verification • Testing and verification complement one another – verification makes assumptions that should be monitored dynamically – testing finds problems that should then be examined globally • Need to develop integrated techniques UMASS Laboratory for Advanced Software Engineering Research

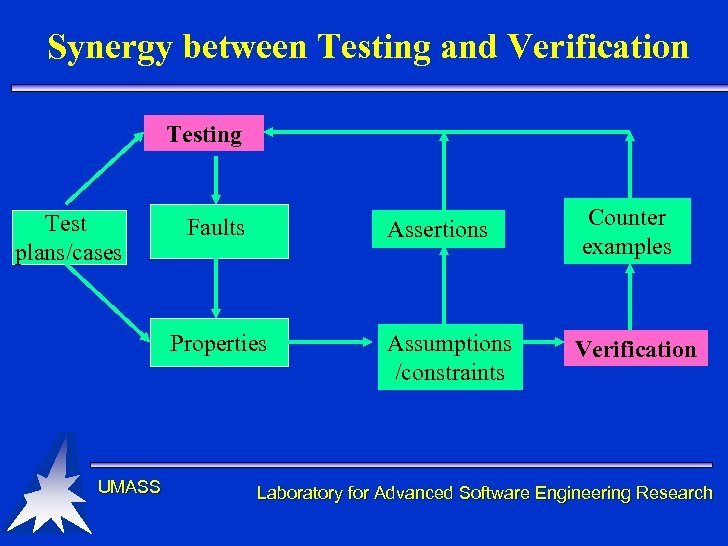Synergy between Testing and Verification Testing Test plans/cases Assertions Faults Properties UMASS Counter examples Assumptions /constraints Verification Laboratory for Advanced Software Engineering Research

Conclusions • Testing alone can not provide the assurance that is needed for many applications – especially distributed systems • FSV a promising technology – Applicable to a wide range of properties – Applicable throughout the lifecycle – Initial empirical results promising UMASS Laboratory for Advanced Software Engineering Research

Conclusion • Finite State Verification is a major paradigm shift – More difficult than testing, but not that much more difficult – Cultural resistance to doing anything different • Is the pain worth the gain? • Grand challenge: Can we lower the obstacles to adoption? UMASS Laboratory for Advanced Software Engineering Research