1698b32e3dd1d744b31a7efb7d834b49.ppt
- Количество слайдов: 40

Finding What We Want: DNS and XPath-Based Pub-Sub Zachary G. Ives University of Pennsylvania CIS 455 / 555 – Internet and Web Systems February 12, 2008

Today § Reminder: HW 1 Milestone 2 due tonight § Directories: DNS § Flooding: Gnutella § XML filtering for pub-sub: XFilter 2
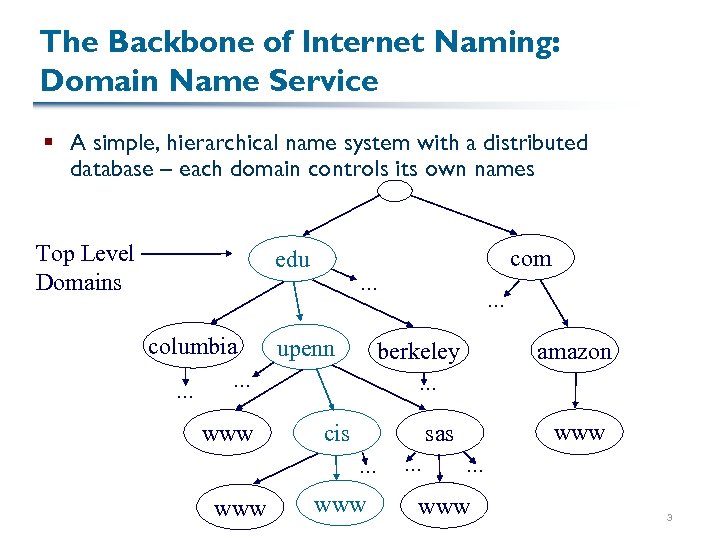
The Backbone of Internet Naming: Domain Name Service § A simple, hierarchical name system with a distributed database – each domain controls its own names Top Level Domains com edu … columbia … upenn berkeley … www amazon … cis www sas … www … … www 3

Top-Level Domains (TLDs) Mostly controlled by Network Solutions, Inc. today. com: commercial. edu: educational institution. gov: US government. mil: US military. net: networks and ISPs (now also a number of other things) §. org: other organizations § 244, 2 -letter country suffixes, e. g. , . us, . uk, . cz, . tv, … § and a bunch of new suffixes that are not very common, e. g. , . biz, . name, . pro, … § § § 4

Finding the Root 13 “root servers” store entries for all top level domains (TLDs) DNS servers have a hard-coded mapping to root servers so they can “get started” 5

Excerpt from DNS Root Server Entries This file is made available by Inter. NIC registration services under anonymous FTP as ; file /domain/named. root ; ; formerly NS. INTERNIC. NET ; . 3600000 IN NS A. ROOT-SERVERS. NET. 3600000 A 98. 41. 0. 4 ; ; formerly NS 1. ISI. EDU ; . 3600000 NS B. ROOT-SERVERS. NET. 3600000 A 128. 9. 0. 107 ; ; formerly C. PSI. NET ; . 3600000 NS C. ROOT-SERVERS. NET. 3600000 A 192. 33. 4. 12 (13 servers in total, A through M) 6

Supposing We Were to Build DNS How would we start? How is a lookup performed? (Hint: what do you need to specify when you add a client to a network that doesn’t do DHCP? ) 7

Issues in DNS § We know that everyone wants to be “mydomain”. com § How does this mesh with the assumptions inherent in our hierarchical naming system? § What happens if things move frequently? § What happens if we want to provide different behavior to different requestors (e. g. , Akamai)? 8

Directories Summarized An efficient way of finding data, assuming: § Data doesn’t change too often, hence it can be replicated and distributed § Hierarchy is relatively “wide and flat” § Caching is present, helping with repeated queries Directories generally rely on names at their core § Sometimes we want to search based on other means, e. g. , predicates or filters over content … 9

Pushing the Search to the Network: Flooding Requests – Gnutella Node A wants a data item; it asks B and C § If B and C don’t have it, they ask their neighbors, etc. § What are the implications of this model? G D H C A E F B I 10

Bringing the Data to the “Router”: Publish. Subscribe § Generally, too much data to store centrally – but perhaps we only need a central coordinator! § Interested parties register a profile with the system (often in a central server) § In, for instance, XPath! § Data gets aggregated at some sort of router or by a crawler, and then gets disseminated to individuals § Based on match between content and the profile § Data changes often, but queries don’t! 11
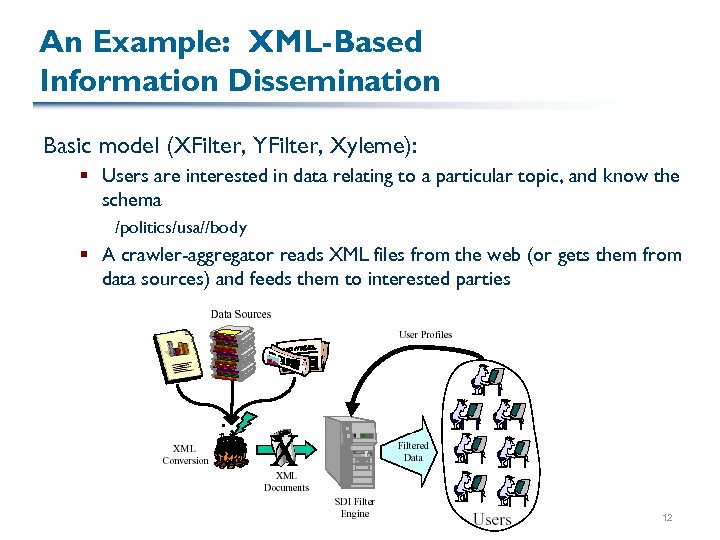
An Example: XML-Based Information Dissemination Basic model (XFilter, YFilter, Xyleme): § Users are interested in data relating to a particular topic, and know the schema /politics/usa//body § A crawler-aggregator reads XML files from the web (or gets them from data sources) and feeds them to interested parties 12
![Engine for XFilter [Altinel & Franklin 00] 13 Engine for XFilter [Altinel & Franklin 00] 13](https://present5.com/presentation/1698b32e3dd1d744b31a7efb7d834b49/image-13.jpg)
Engine for XFilter [Altinel & Franklin 00] 13

How Does It Work? § Each XPath segment is basically a subset of regular expressions over element tags § Convert into finite state automata § Parse data as it comes in – use SAX API § Match against finite state machines § Most of these systems use modified FSMs because they want to match many patterns at the same time 14

Path Nodes and FSMs § XPath parser decomposes XPath expressions into a set of path nodes § These nodes act as the states of corresponding FSM § A node in the Candidate List denotes the current state § The rest of the states are in corresponding Wait Lists § Simple FSM for /politics[@topic=“president”]/usa//body: politics Q 1_1 usa Q 1_2 body Q 1_3 15
![Decomposing Into Path Nodes Q 1=/politics[@topic=“president”]/usa//body Query ID Q 1 Q 1 Position in Decomposing Into Path Nodes Q 1=/politics[@topic=“president”]/usa//body Query ID Q 1 Q 1 Position in](https://present5.com/presentation/1698b32e3dd1d744b31a7efb7d834b49/image-16.jpg)
Decomposing Into Path Nodes Q 1=/politics[@topic=“president”]/usa//body Query ID Q 1 Q 1 Position in state machine 1 2 3 Relative Position (RP) in tree: 0 for root node if it’s not 0 1 -1 preceded by “//” 1 2 -1 -1 for any node preceded by “//” Q 1 -1 Q 1 -2 Q 1 -3 Q 2=//usa/*/body/p Q 2 1 2 -1 0 Q 2 3 1 0 Q 2 -1 Q 2 -2 Q 2 -3 Else =1+ (no of “*” nodes from predecessor node) Level: If current node has fixed distance from root, then 1+ distance Else if RP = – 1, then – 1, else 0 Finaly, Next. Path. Node. Set points to next node 16
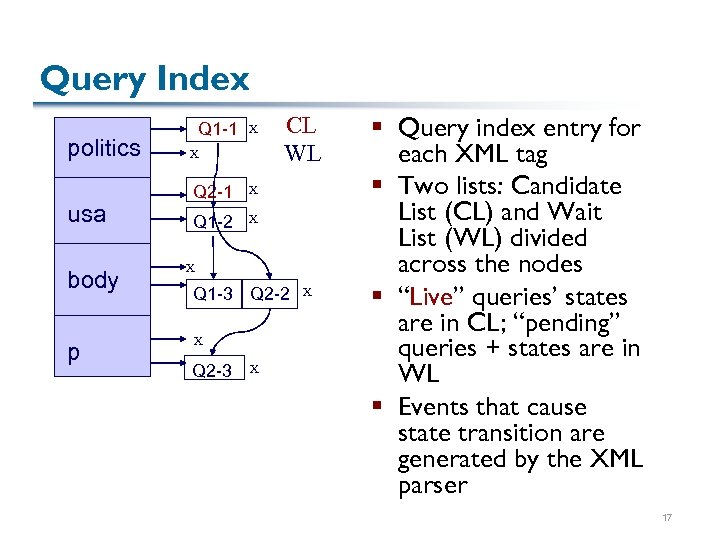
Query Index politics usa body p Q 1 -1 X X Q 2 -1 X Q 1 -2 CL WL X X Q 1 -3 Q 2 -2 X Q 2 -3 X X § Query index entry for each XML tag § Two lists: Candidate List (CL) and Wait List (WL) divided across the nodes § “Live” queries’ states are in CL; “pending” queries + states are in WL § Events that cause state transition are generated by the XML parser 17
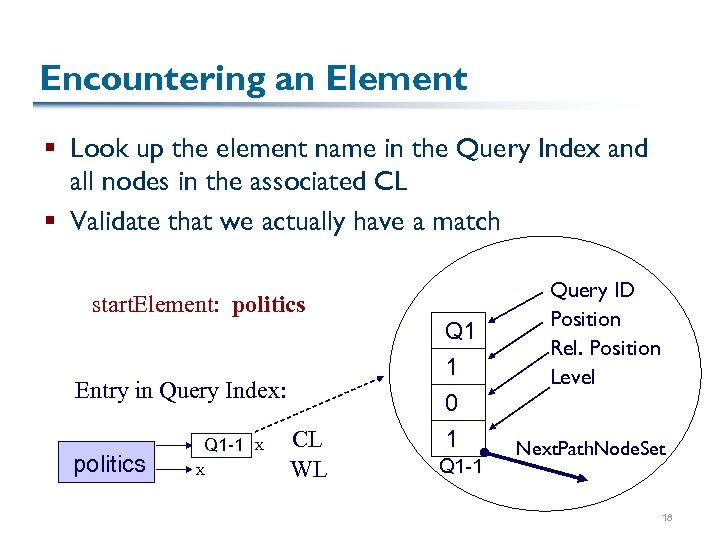
Encountering an Element § Look up the element name in the Query Index and all nodes in the associated CL § Validate that we actually have a match start. Element: politics Entry in Query Index: politics Q 1 -1 X X CL WL Q 1 1 0 1 Q 1 -1 Query ID Position Rel. Position Level Next. Path. Node. Set 18

Validating a Match § We first check that the current XML depth matches the level in the user query: § If level in CL node is less than 1, then ignore height § else level in CL node must = height § This ensures we’re matching at the right point in the tree! § Finally, we validate any predicates against attributes (e. g. , [@topic=“president”]) 19

Processing Further Elements § Queries that don’t meet validation are removed from the Candidate Lists § For other queries, we advance to the next state § We copy the next node of the query from the WL to the CL, and update the RP and level § When we reach a final state (e. g. , Q 1 -3), we can output the document to the subscriber § When we encounter an end element, we must remove that element from the CL 20

Publish-Subscribe Model Summarized § Currently not commonly used § Partly because XML isn’t that widespread § This may change with the adoption of an XML format called RSS (Rich Site Summary or Really Simple Syndication) Many news sites, web logs, mailing lists, etc. use RSS to publish daily articles § Seems like a perfect fit for publish-subscribe models! 21

Finding a Happy Medium We’ve seen two approaches: § Do all the work at the data stores: flood the network with requests § Do all the work via a central crawler: record profiles and disseminate matches § An alternative, two-step process: § Build a content index over what’s out there § Typically limited in what kinds of queries can be supported § Most common instance: an index of document keywords 22

Inverted Indices § A conceptually very simple data structure: <keyword, {list of occurrences}> § In its simplest form, each occurrence includes a document pointer (e. g. , URI), perhaps a count and/or position § Requires two components, an indexer and a retrieval system § We’ll consider cost of building the index, plus searching the index using a single keyword 23

How Do We Lay Out an Inverted Index? § Some options: § § Unordered list Ordered list Tree Hash table 24

Unordered and Ordered Lists § Assume that we have entries such as: <keyword, #items, {list of occurrences}> § What does ordering buy us? § Assume that we adopt a model in which we use: <keyword, item> § Do we get any additional benefits? § How about: <keyword, {items}> where we fix the size of the keyword and the number of items? 25

Tree-Based Indices Trees have several benefits over lists: § Potentially logarithmic search time, as with a well, designed sorted list, IF it’s balanced § Ability to handle variable-length records We’ve already seen how trees might make a natural way of distributing data, as well How does a binary search tree fare? § Cost of building? § Cost of finding an item in it? 26
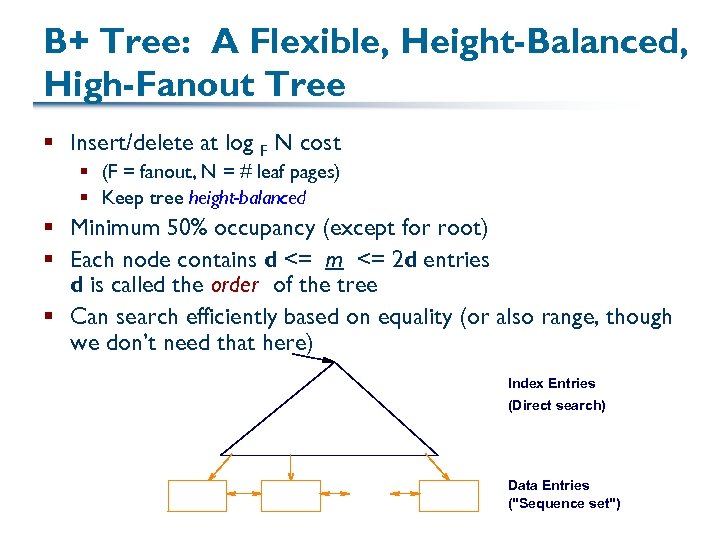
B+ Tree: A Flexible, Height-Balanced, High-Fanout Tree § Insert/delete at log F N cost § (F = fanout, N = # leaf pages) § Keep tree height-balanced § Minimum 50% occupancy (except for root) § Each node contains d <= m <= 2 d entries d is called the order of the tree § Can search efficiently based on equality (or also range, though we don’t need that here) Index Entries (Direct search) Data Entries ("Sequence set")
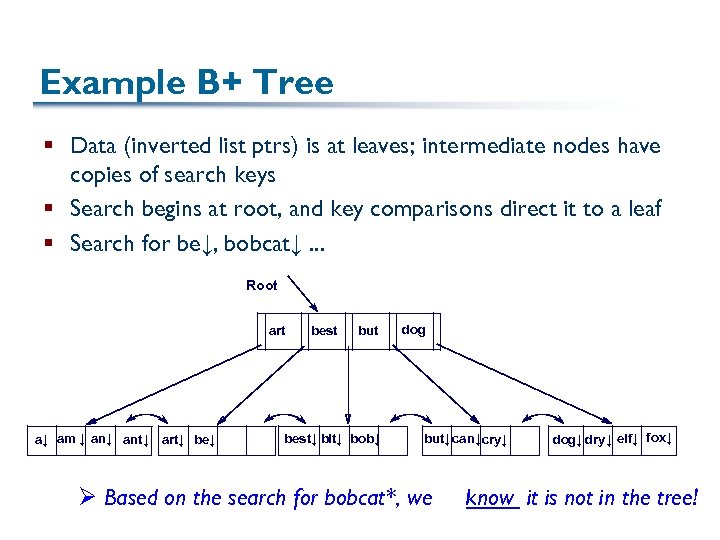
Example B+ Tree § Data (inverted list ptrs) is at leaves; intermediate nodes have copies of search keys § Search begins at root, and key comparisons direct it to a leaf § Search for be↓, bobcat↓. . . Root art a↓ am ↓ ant↓ art↓ best but best↓ bit↓ bob↓ dog but↓ can↓ cry↓ Ø Based on the search for bobcat*, we dog↓ dry↓ elf↓ fox↓ know it is not in the tree!

B+ Trees in Practice § Typical order: 100. Typical fill-factor: 67%. § average fanout = 133 § Typical capacities: § Height 4: 1334 = 312, 900, 700 records § Height 3: 1333 = 2, 352, 637 records § Can often hold top levels in a cache: § Level 1 = 1 page = 8 Kbytes § Level 2 = 133 pages = 1 Mbyte § Level 3 = 17, 689 pages = 133 MBytes

Inserting Data into a B+ Tree § Find correct leaf L § Put data entry onto L § If L has enough space, done! § Else, must split L (into L and a new node L 2) Redistribute entries evenly, copy up middle key Insert index entry pointing to L 2 into parent of L § This can happen recursively § To split index node, redistribute entries evenly, but push up middle key. (Contrast with leaf splits. ) § Splits “grow” tree; root split increases height § Tree growth: gets wider or one level taller at top

Inserting “and into Example B+ Tree ↓” § Observe how minimum occupancy is guaranteed in both leaf and index page splits § Recall that all data items are in leaves, and partition values for keys are in intermediate nodes Note difference between copy-up and push-up
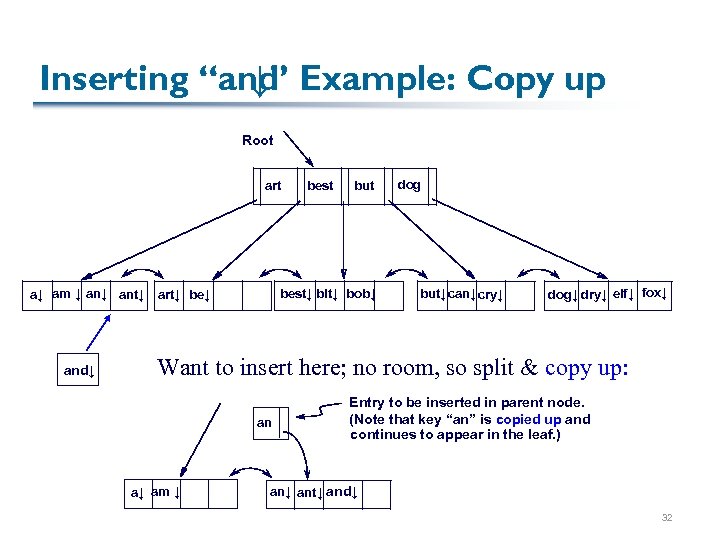
Inserting “and Example: Copy up ↓” Root art but best↓ bit↓ bob↓ a↓ am ↓ ant↓ art↓ be↓ and↓ best dog but↓ can↓ cry↓ dog↓ dry↓ elf↓ fox↓ Want to insert here; no room, so split & copy up: an a↓ am ↓ Entry to be inserted in parent node. (Note that key “an” is copied up and continues to appear in the leaf. ) an↓ ant↓ and↓ 32
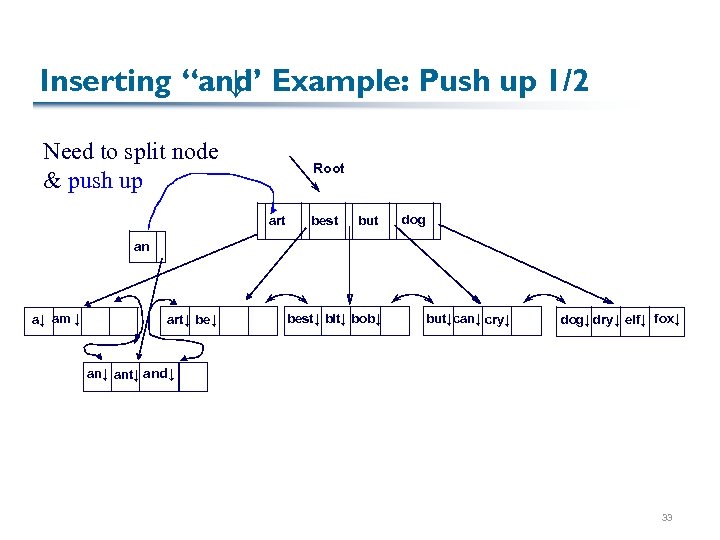
Inserting “and Example: Push up 1/2 ↓” Need to split node & push up Root art best but dog an a↓ am ↓ art↓ best↓ bit↓ bob↓ but↓can↓ cry↓ dog↓ dry↓ elf↓ fox↓ ant↓ and↓ 33
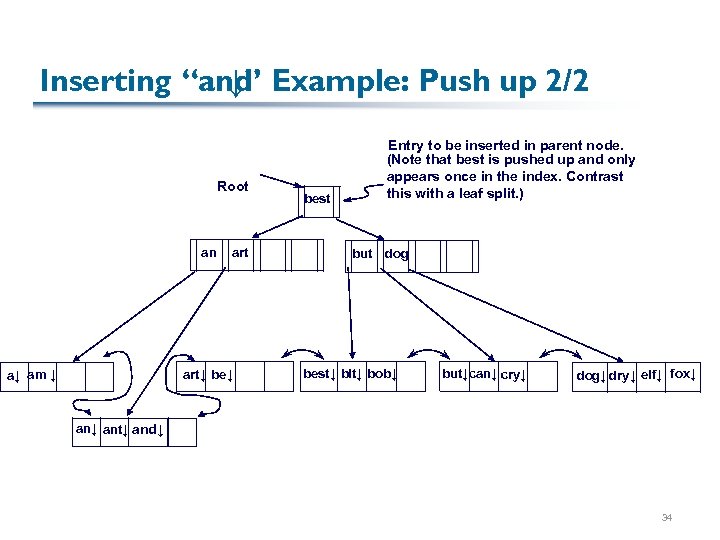
Inserting “and Example: Push up 2/2 ↓” Root an a↓ am ↓ art↓ best Entry to be inserted in parent node. (Note that best is pushed up and only appears once in the index. Contrast this with a leaf split. ) but dog best↓ bit↓ bob↓ but↓can↓ cry↓ dog↓ dry↓ elf↓ fox↓ ant↓ and↓ 34

Copying vs. Splitting, Summarized § Every keyword (search key) appears in at most one intermediate node § Hence, in splitting an intermediate node, we push up § Every inverted list entry must appear in the leaf § We may also need it in an intermediate node to define a partition point in the tree § We must copy up the key of this entry § Note that B+ trees easily accommodate multiple occurrences of a keyword 35

Virtues of the B+ Tree B+ tree and other indices are quite efficient: § § Height-balanced; log. F N cost to search High fanout (F) means depth rarely more than 3 or 4 Almost always better than maintaining a sorted file Typically, 67% occupancy on average
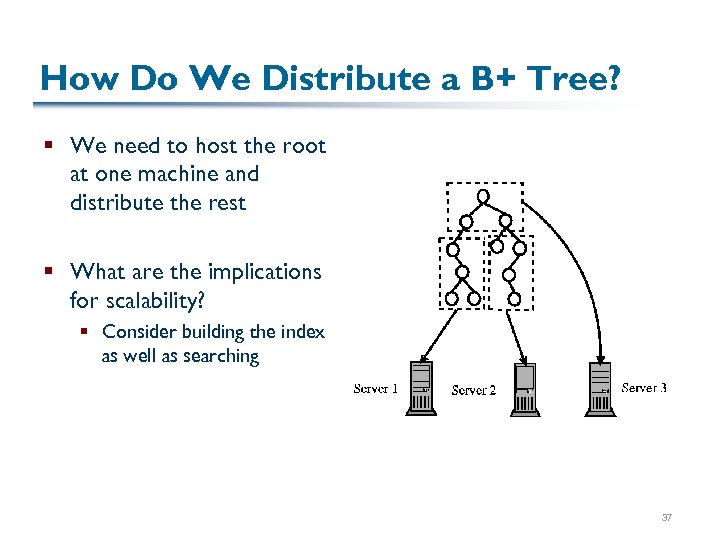
How Do We Distribute a B+ Tree? § We need to host the root at one machine and distribute the rest § What are the implications for scalability? § Consider building the index as well as searching 37

Eliminating the Root § Sometimes we don’t want a tree-structured system because the higher levels can be a central point of congestion or failure 38
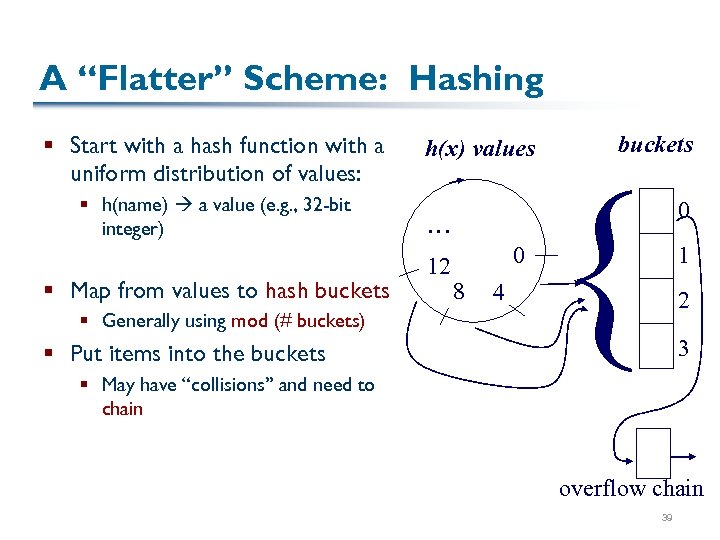
A “Flatter” Scheme: Hashing § Start with a hash function with a uniform distribution of values: § h(name) a value (e. g. , 32 -bit integer) § Map from values to hash buckets § Generally using mod (# buckets) § Put items into the buckets h(x) values … 12 0 8 4 buckets { 0 1 2 3 § May have “collisions” and need to chain overflow chain 39

Next: Data Distribution § Going from hashing to distributed hashing 40
1698b32e3dd1d744b31a7efb7d834b49.ppt