Finding Mathematics in Genes and Diseases Ming-Ying Leung

Finding Mathematics in Genes and Diseases Ming-Ying Leung Department of Mathematical Sciences University of Texas at El Paso (UTEP)

“ 1, 2, 3, … and Beyond” • A slideshow for HKU Open Day in 1980 • I did the narration and background music • The experience has a great impact on my journey Mathematics is beyond numbers… We find it in buildings, banks, and supermarkets… …in atoms, molecules, and genes …

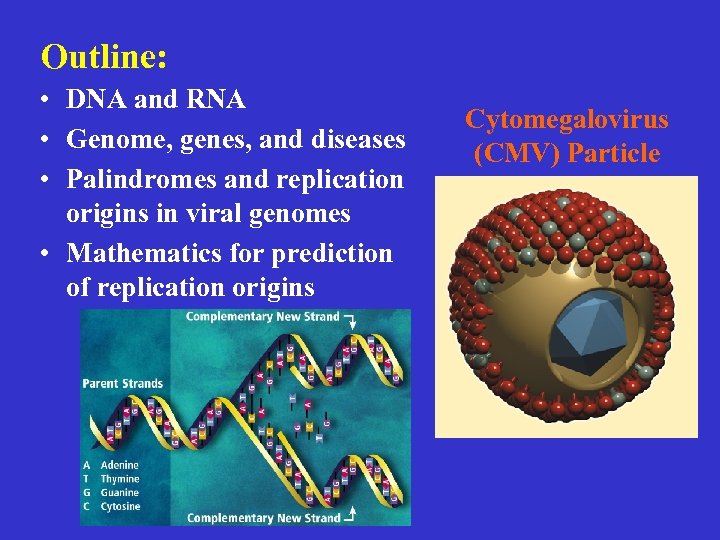Outline: • DNA and RNA • Genome, genes, and diseases • Palindromes and replication origins in viral genomes • Mathematics for prediction of replication origins Cytomegalovirus (CMV) Particle

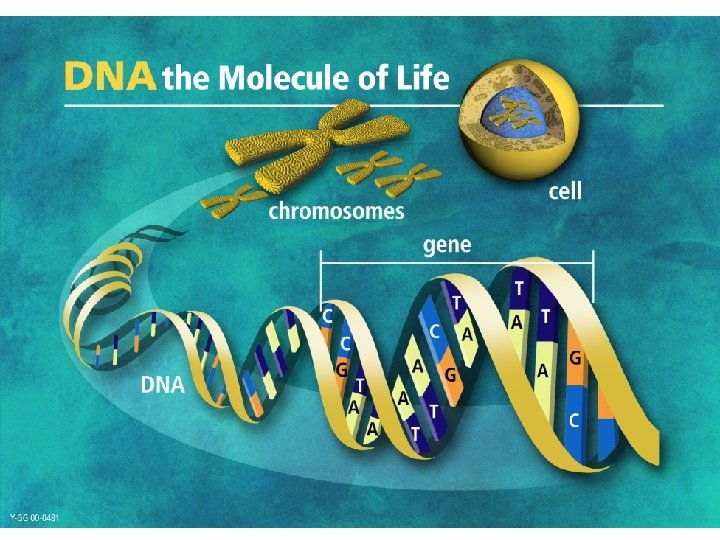
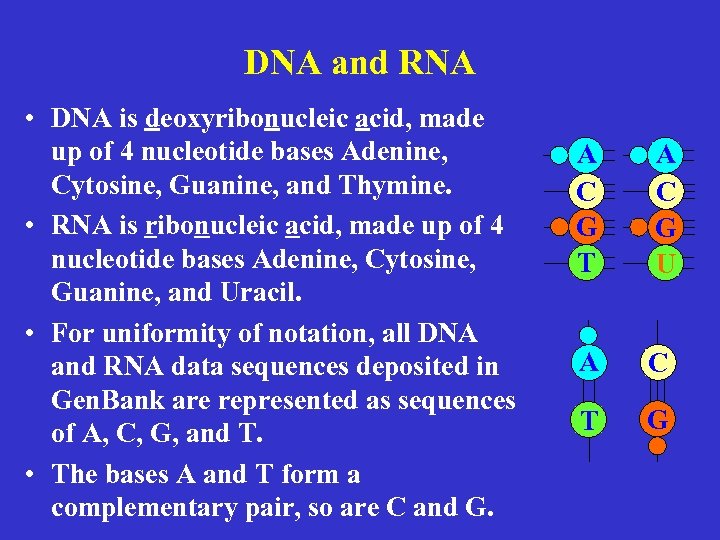DNA and RNA • DNA is deoxyribonucleic acid, made up of 4 nucleotide bases Adenine, Cytosine, Guanine, and Thymine. • RNA is ribonucleic acid, made up of 4 nucleotide bases Adenine, Cytosine, Guanine, and Uracil. • For uniformity of notation, all DNA and RNA data sequences deposited in Gen. Bank are represented as sequences of A, C, G, and T. • The bases A and T form a complementary pair, so are C and G. A C G T A C G U A C T G

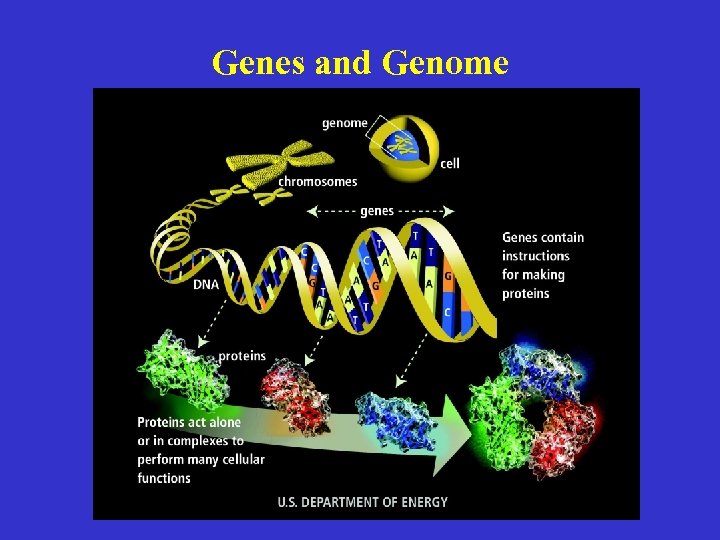Genes and Genome

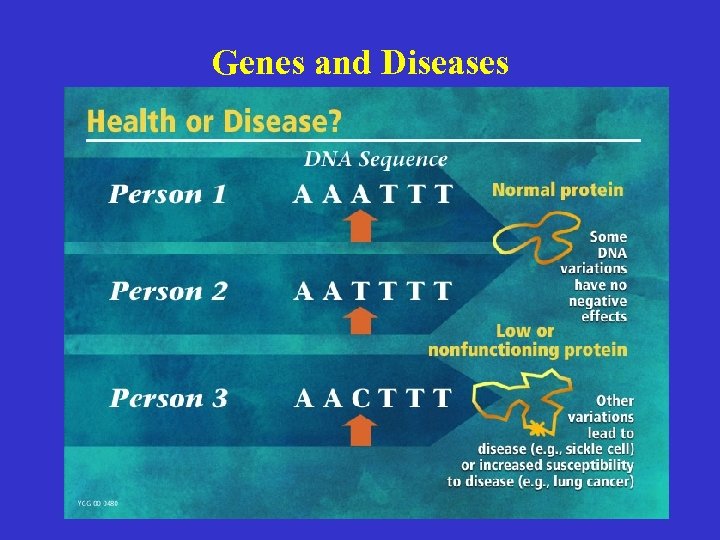Genes and Diseases

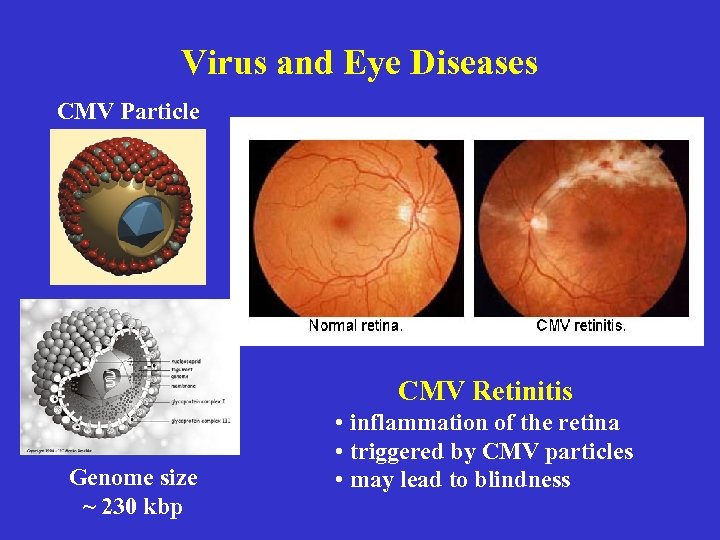Virus and Eye Diseases CMV Particle CMV Retinitis Genome size ~ 230 kbp • inflammation of the retina • triggered by CMV particles • may lead to blindness

Replication Origins and Palindromes • High concentration of palindromes exists around replication origins of other herpesviruses • Locating clusters of palindromes (above a minimal length) on CMV genome sequence might reveal likely locations of its replication origins.

Palindromes in Letter Sequences Odd Palindrome: “A nut for a jar of tuna” remove spaces and capitalize ANUTFORAJAROFTUNA Even Palindrome: “Step on no pets” STEPON NOPETS

DNA Palindromes

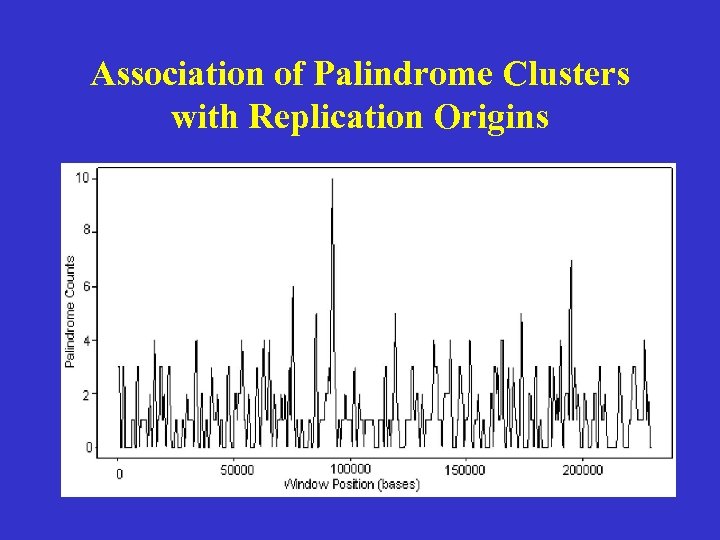Association of Palindrome Clusters with Replication Origins

Computational Prediction of Replication Origins • Palindrome distribution in a random sequence model • Criterion for identifying statistically significant palindrome clusters • Evaluate prediction accuracy • Try to improve…

Random Sequence Model • A mathematical model can be used to generate a DNA sequence • A DNA molecule is made up of 4 types of bases • It can be represented by a letter sequence with alphabet size = 4 • • Adenosine Cytosine Guanine Thymine A C G T Wheel of Bases (WOB)

Random Sequence Model Each type of the bases has its chance (or probability) of being used, depending on the base composition of the DNA molecule. • • Adenosine Cytosine Guanine Thymine A C G T Wheel of Bases (WOB)

Poisson Process Approximation of Palindrome Distribution

Use of the Scan Statistic to Identify Clusters of Palindromes

Measures of Prediction Accuracy Attempts to improve prediction accuracy by: • Adopting the best possible approximation to the scan statistic distribution • Taking the lengths of palindromes into consideration when counting palindromes • Using a better random sequence model

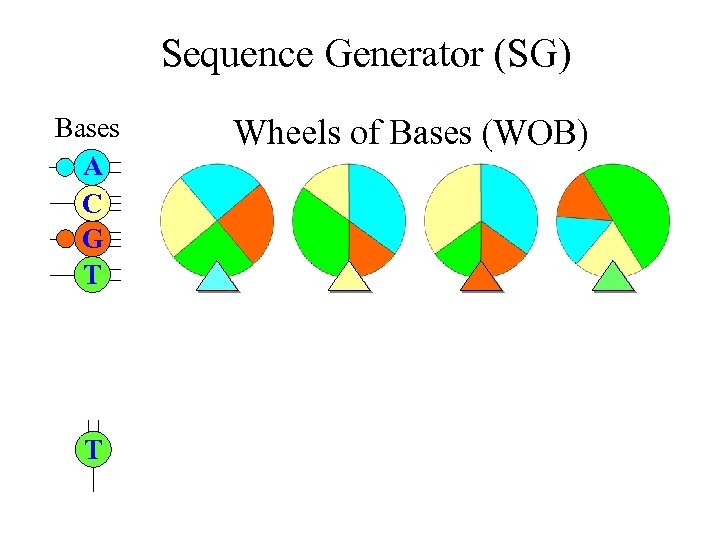
Markov Chain Sequence Models • More realistic random sequence model for DNA and RNA • It allows neighbor dependence of bases (i. e. , the present base will affect the selection of bases for the next base) • A Markov chain of nucleotide bases can be generated using four WOBs in a “Sequence Generator (SG)”

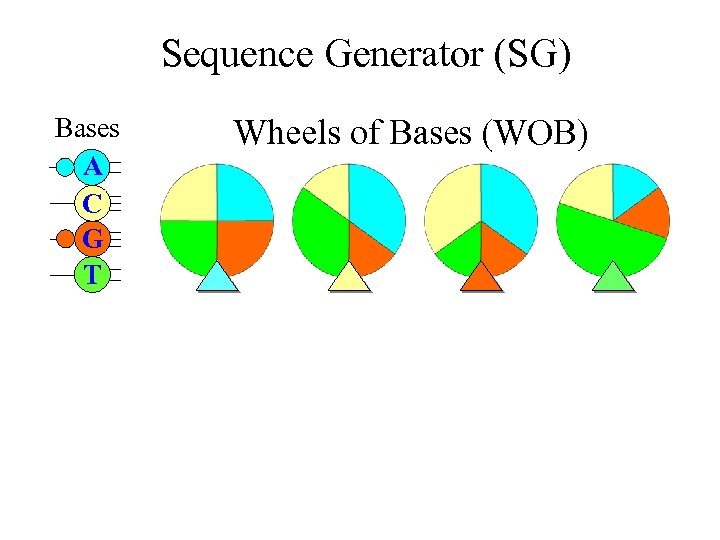Sequence Generator (SG) Bases A C G T Wheels of Bases (WOB)

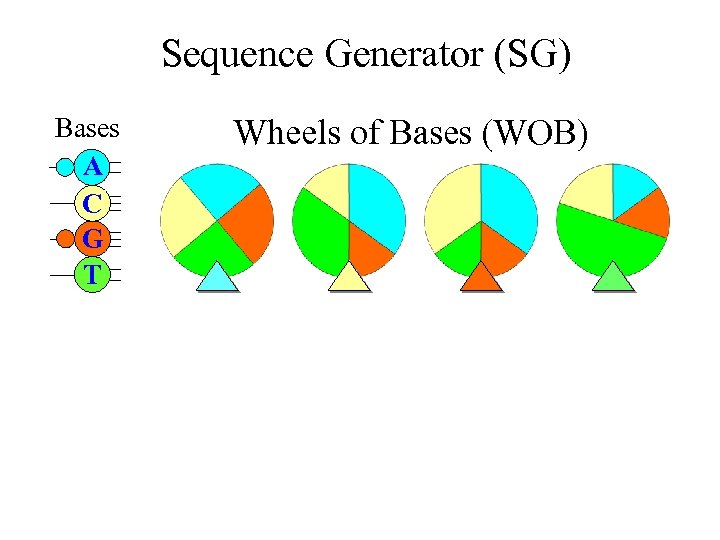Sequence Generator (SG) Bases A C G T T Wheels of Bases (WOB)

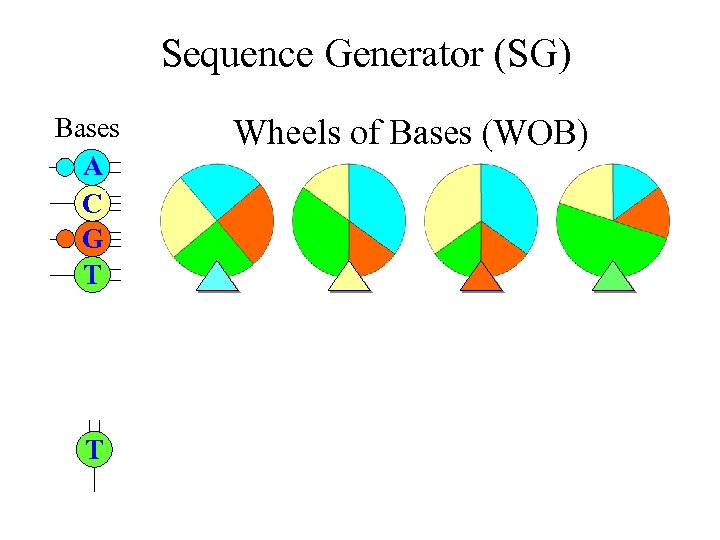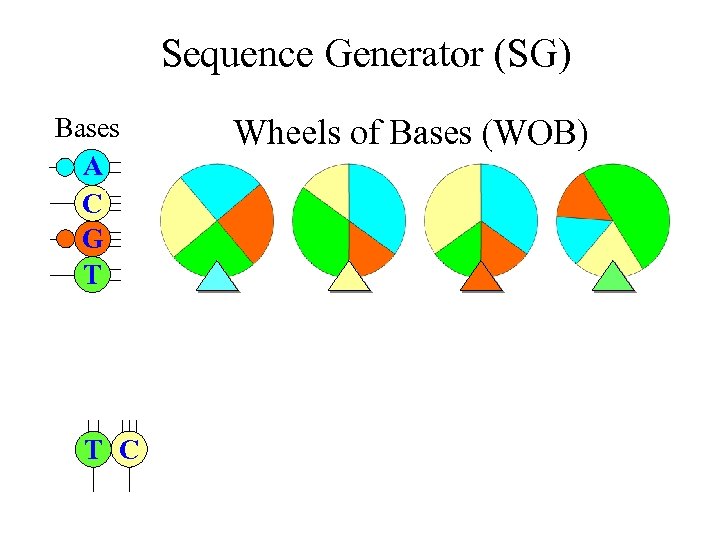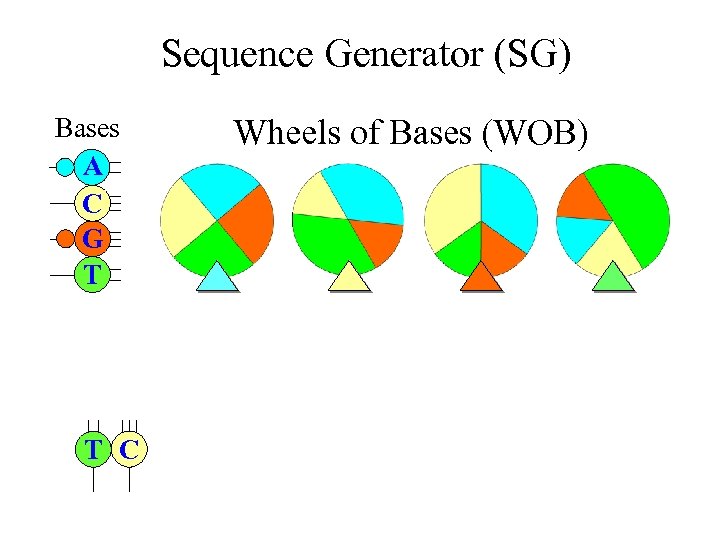Sequence Generator (SG) Bases A C G T T C Wheels of Bases (WOB)

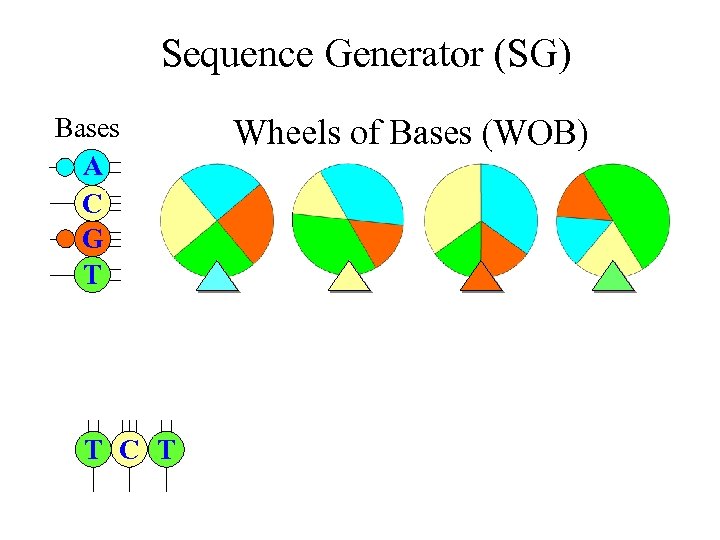Sequence Generator (SG) Bases A C G T T C T Wheels of Bases (WOB)

Sequence Generator (SG) Bases A C G T T C T T Wheels of Bases (WOB)

Sequence Generator (SG) Bases A C G T Wheels of Bases (WOB) T C T T T

Sequence Generator (SG) Bases A C G T Wheels of Bases (WOB) T C T T T A

Sequence Generator (SG) Bases A C G T Wheels of Bases (WOB) T C T T T A A

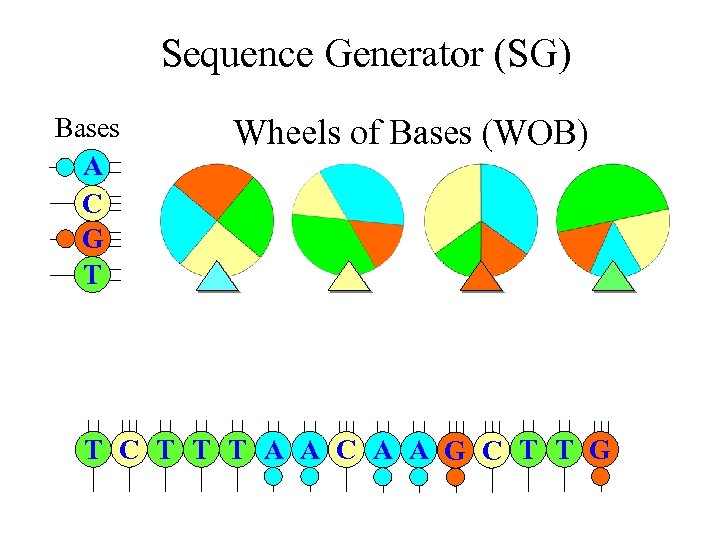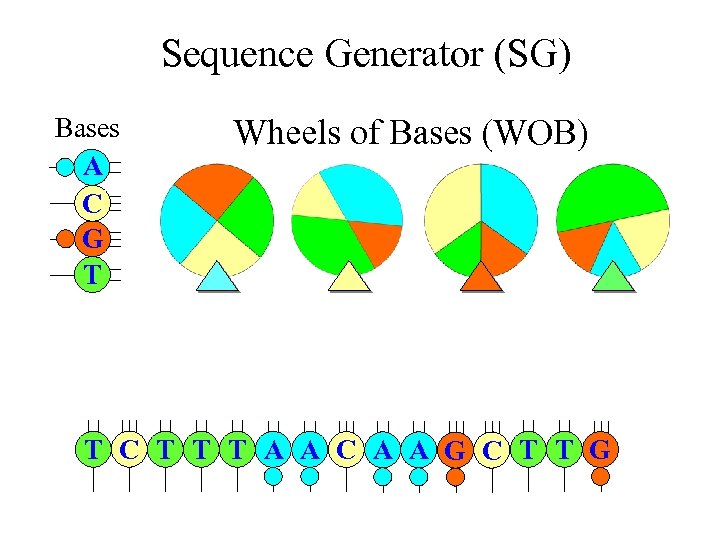Sequence Generator (SG) Bases A C G T Wheels of Bases (WOB) T C T T T A A C A A G C T T G

Results Obtained for Markov Sequence Models • Probabilities of occurrences of single palindromes • Probabilities of occurrences of overlapping palindromes • Mean and variance of palindrome counts

Related Work in Progress • Finding the palindrome distribution on Markov random sequences • Investigating other sequence patterns such as close repeats and inversions in relation to replication origins

Other Mathematical Topics in Genes and Diseases • Optimization Techniques – prediction of molecular structures • Differential Equations – molecular dynamics • Matrix Theory – analyzing gene expression data • Fourier Analysis – proteomics data

Acknowledgements Collaborators Louis H. Y. Chen (National University of Singapore) David Chew (National University of Singapore) Kwok Pui Choi (National University of Singapore) Aihua Xia (University of Melbourne, Australia) Funding Support NIH Grants S 06 GM 08194 -23, S 06 GM 08194 -24, and 2 G 12 RR 008124 NSF DUE 9981104 W. M. Keck Center of Computational & Struct. Biol. at Rice University National Univ. of Singapore ARF Research Grant (R-146 -000 -013 -112) Singapore BMRC Grants 01/21/19/140 and 01/1/21/19/217

St. Stephen’s Girls’ College

University of Hong Kong Department of Mathematics: A Beach Picnic

Continuing to Find Mathematics in Genes and Diseases Ming-Ying Leung Department of Mathematical Sciences University of Texas at El Paso (UTEP)