Финансовая математика - Тема 10.pptx
- Количество слайдов: 36
 ФИНАНСОВАЯ МАТЕМАТИКА Силина Татьяна Леонидовна
ФИНАНСОВАЯ МАТЕМАТИКА Силина Татьяна Леонидовна
 Тема 10. Финансовые функции EXCEL как основа практических расчетов 10. 1. Сущность финансовых функций Сегодня нельзя всерьез претендовать на работу экономиста, менеджера, бухгалтера, финансиста, специалиста по ценным бумагам и т. п. , если не уметь обращаться с компьютером. Умение работы с компьютером предполагает прежде всего знание текстовых процессоров, электронных таблиц, системы управления базами данных и систем для работы с графикой.
Тема 10. Финансовые функции EXCEL как основа практических расчетов 10. 1. Сущность финансовых функций Сегодня нельзя всерьез претендовать на работу экономиста, менеджера, бухгалтера, финансиста, специалиста по ценным бумагам и т. п. , если не уметь обращаться с компьютером. Умение работы с компьютером предполагает прежде всего знание текстовых процессоров, электронных таблиц, системы управления базами данных и систем для работы с графикой.
 Тема 10. Финансовые функции EXCEL как основа практических расчетов На основной панели инструментов имеется кнопка "Мастер функций", с помощью которой открывается диалоговое окно Диспетчера функций. Оно организовано по тематическому принципу. Выбрав в левом списке тематическую группу Финансовые, получите полный перечень списка имен функций, содержащихся в данной группе.
Тема 10. Финансовые функции EXCEL как основа практических расчетов На основной панели инструментов имеется кнопка "Мастер функций", с помощью которой открывается диалоговое окно Диспетчера функций. Оно организовано по тематическому принципу. Выбрав в левом списке тематическую группу Финансовые, получите полный перечень списка имен функций, содержащихся в данной группе.
 Тема 10. Финансовые функции EXCEL как основа практических расчетов При работе с финансовыми функциями необходимо учитывать специфику задания значения аргументов: можно вводить как сами значения аргументов, так и ссылки на адреса ячеек; все расходы денежных средств (платежи) представляются отрицательными числами, а все поступления денежных средств – положительными числами; процентная ставка вводится с использованием знака %; все даты как аргументы функций имеют числовой формат.
Тема 10. Финансовые функции EXCEL как основа практических расчетов При работе с финансовыми функциями необходимо учитывать специфику задания значения аргументов: можно вводить как сами значения аргументов, так и ссылки на адреса ячеек; все расходы денежных средств (платежи) представляются отрицательными числами, а все поступления денежных средств – положительными числами; процентная ставка вводится с использованием знака %; все даты как аргументы функций имеют числовой формат.
 Тема 10. Финансовые функции EXCEL как основа практических расчетов 10. 1. Операции наращения Функция БЗ – будущее значение – рассчитывает наращенную величину разовой денежной суммы или периодических постоянных платежей на основе постоянной процентной ставки. С ее помощью можно упростить расчет FV или FVA. Аргументы данной функции: норма; число периодов; выплата; НЗ; тип.
Тема 10. Финансовые функции EXCEL как основа практических расчетов 10. 1. Операции наращения Функция БЗ – будущее значение – рассчитывает наращенную величину разовой денежной суммы или периодических постоянных платежей на основе постоянной процентной ставки. С ее помощью можно упростить расчет FV или FVA. Аргументы данной функции: норма; число периодов; выплата; НЗ; тип.
 Тема 10. Финансовые функции EXCEL как основа практических расчетов Для правильного ввода аргументов необходимо идентифицировать их с классическими обозначениями: норма – процентная ставка (i); число периодов – срок финансовой операции или общее число раз начисления процентов за весь срок финансовой операции (n или m╥n); выплата – член финансовой ренты (R); НЗ – начальное значение, т. е. первоначальная сума долга (PV); тип – вид финансовой ренты в зависимости от метода выплаты платежей: платежи в конце периода, т. е. обычная рента или пренумерандо число 1, платежи в начале периода, т. е. постнумерандо число 0.
Тема 10. Финансовые функции EXCEL как основа практических расчетов Для правильного ввода аргументов необходимо идентифицировать их с классическими обозначениями: норма – процентная ставка (i); число периодов – срок финансовой операции или общее число раз начисления процентов за весь срок финансовой операции (n или m╥n); выплата – член финансовой ренты (R); НЗ – начальное значение, т. е. первоначальная сума долга (PV); тип – вид финансовой ренты в зависимости от метода выплаты платежей: платежи в конце периода, т. е. обычная рента или пренумерандо число 1, платежи в начале периода, т. е. постнумерандо число 0.
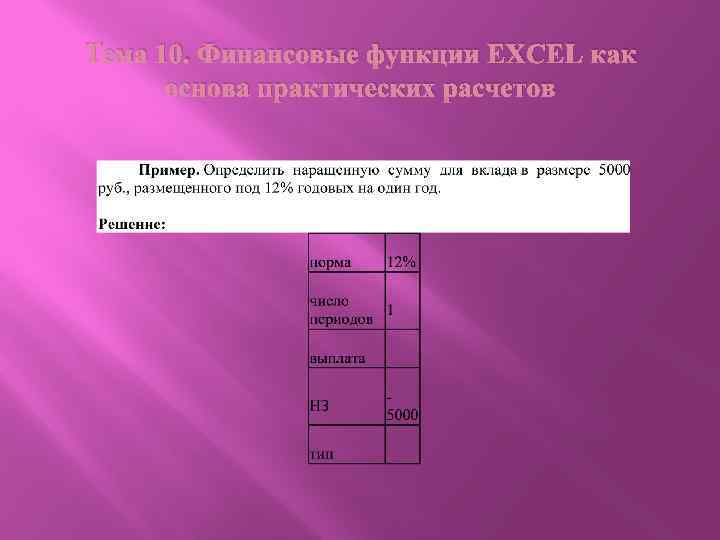
 Тема 10. Финансовые функции EXCEL как основа практических расчетов Простые проценты. Для решения задач наращения по простым процентам следует помнить, что не все аргументы рассматриваемой функции используются в этом случае. Рабочими аргументами являются: норма; число периодов; НЗ.
Тема 10. Финансовые функции EXCEL как основа практических расчетов Простые проценты. Для решения задач наращения по простым процентам следует помнить, что не все аргументы рассматриваемой функции используются в этом случае. Рабочими аргументами являются: норма; число периодов; НЗ.
 Тема 10. Финансовые функции EXCEL как основа практических расчетов
Тема 10. Финансовые функции EXCEL как основа практических расчетов
 Тема 10. Финансовые функции EXCEL как основа практических расчетов В верхней части диалогового окна Ввода аргументов функции в ячейке "Значение" появится ответ: 5600, 00. Таким образом, через год наращенная сумма составит 5'600, 00 руб. Обратите внимание, что в аргументах годовой процент и целое число лет. Если продолжительность финансовой операции представлена в днях, то необходимо ввести корректировку в процентную ставку, т. е. аргумент норма будет представлен как t/T • i%.
Тема 10. Финансовые функции EXCEL как основа практических расчетов В верхней части диалогового окна Ввода аргументов функции в ячейке "Значение" появится ответ: 5600, 00. Таким образом, через год наращенная сумма составит 5'600, 00 руб. Обратите внимание, что в аргументах годовой процент и целое число лет. Если продолжительность финансовой операции представлена в днях, то необходимо ввести корректировку в процентную ставку, т. е. аргумент норма будет представлен как t/T • i%.
 Тема 10. Финансовые функции EXCEL как основа практических расчетов
Тема 10. Финансовые функции EXCEL как основа практических расчетов
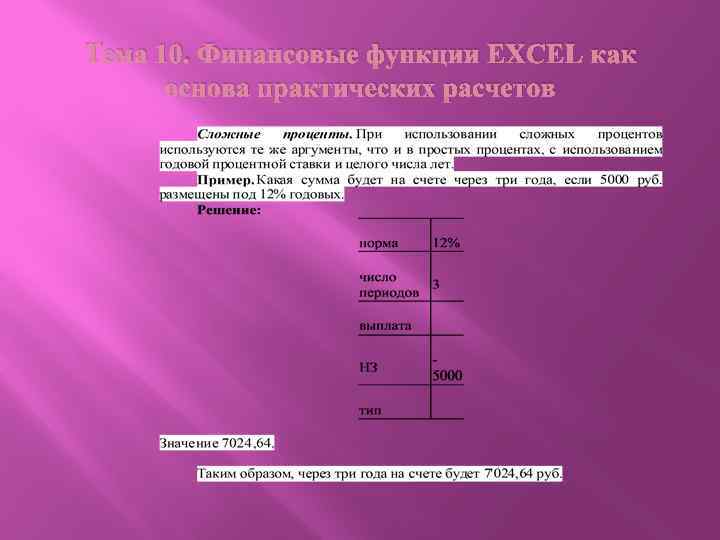
 Тема 10. Финансовые функции EXCEL как основа практических расчетов Если же период начисления процентов будет меньше года, то необходимо модифицировать аргументы норма и число периодов: норма – берется ставка процентов за период начисления, т. е. используется номинальная годовая ставка процентов, скорректированная на число раз начисления процентов в течение года j% / m; число периодов – указывается общее число раз начисления процентов за весь срок финансовой операции n • m.
Тема 10. Финансовые функции EXCEL как основа практических расчетов Если же период начисления процентов будет меньше года, то необходимо модифицировать аргументы норма и число периодов: норма – берется ставка процентов за период начисления, т. е. используется номинальная годовая ставка процентов, скорректированная на число раз начисления процентов в течение года j% / m; число периодов – указывается общее число раз начисления процентов за весь срок финансовой операции n • m.
 Тема 10. Финансовые функции EXCEL как основа практических расчетов Значение 7092, 60.
Тема 10. Финансовые функции EXCEL как основа практических расчетов Значение 7092, 60.
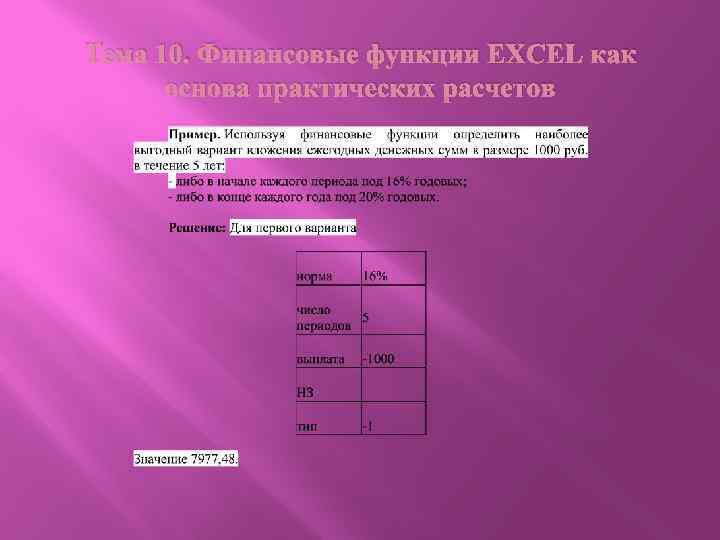
 Тема 10. Финансовые функции EXCEL как основа практических расчетов Финансовые ренты. Наращенная величина аннуитета может быть рассчитана при использовании следующего набора аргументов: норма; число периодов; выплата; тип.
Тема 10. Финансовые функции EXCEL как основа практических расчетов Финансовые ренты. Наращенная величина аннуитета может быть рассчитана при использовании следующего набора аргументов: норма; число периодов; выплата; тип.
 Тема 10. Финансовые функции EXCEL как основа практических расчетов
Тема 10. Финансовые функции EXCEL как основа практических расчетов
 Тема 10. Финансовые функции EXCEL как основа практических расчетов
Тема 10. Финансовые функции EXCEL как основа практических расчетов
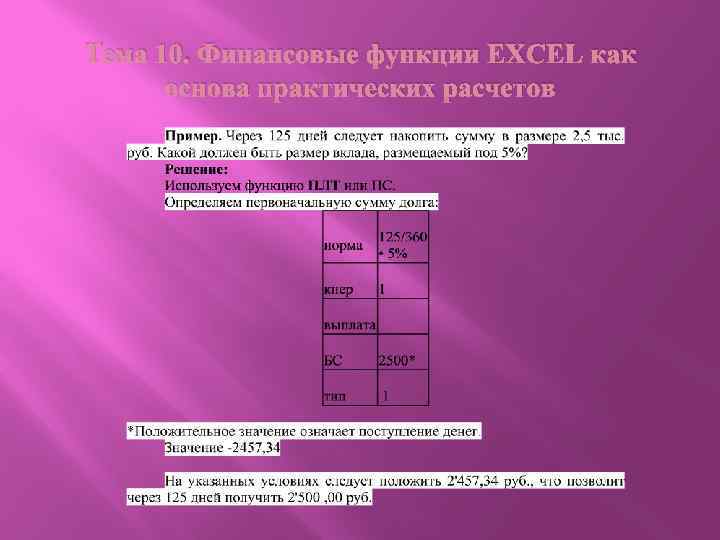
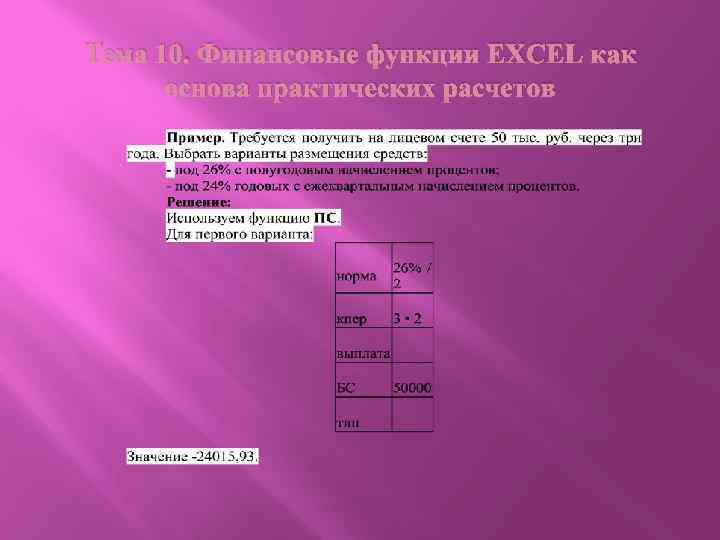
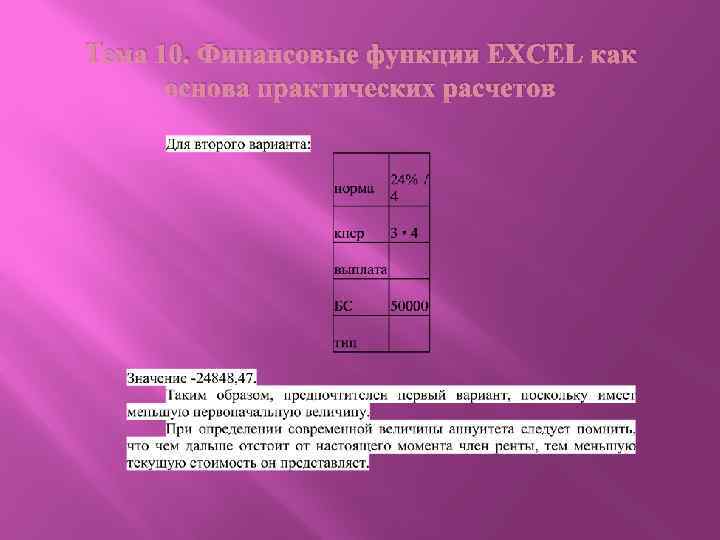
 Тема 10. Финансовые функции EXCEL как основа практических расчетов Операции дисконтирования Для многих финансовых операций необходимо использовать данные о приведенных или современных денежных величинах, как разовой суммы, так и потоков фиксированных периодических платежей. Для облегчения расчетов используется функция ПЗ – первоначальное значение (PV). Аргументы функции: норма; кпер; выплата; БС; тип. Этот расчет является обратным к определению наращенной суммы при помощи функции БЗ, поэтому сущность используемых аргументов в этих функциях аналогична. Вместе с тем, вводится новый аргумент БС – будущая стоимость или будущее значение денежной суммы (FV), а также иное обозначение числа периодов – кпер – (n или n • m).
Тема 10. Финансовые функции EXCEL как основа практических расчетов Операции дисконтирования Для многих финансовых операций необходимо использовать данные о приведенных или современных денежных величинах, как разовой суммы, так и потоков фиксированных периодических платежей. Для облегчения расчетов используется функция ПЗ – первоначальное значение (PV). Аргументы функции: норма; кпер; выплата; БС; тип. Этот расчет является обратным к определению наращенной суммы при помощи функции БЗ, поэтому сущность используемых аргументов в этих функциях аналогична. Вместе с тем, вводится новый аргумент БС – будущая стоимость или будущее значение денежной суммы (FV), а также иное обозначение числа периодов – кпер – (n или n • m).
 Тема 10. Финансовые функции EXCEL как основа практических расчетов
Тема 10. Финансовые функции EXCEL как основа практических расчетов
 Тема 10. Финансовые функции EXCEL как основа практических расчетов
Тема 10. Финансовые функции EXCEL как основа практических расчетов
 Тема 10. Финансовые функции EXCEL как основа практических расчетов
Тема 10. Финансовые функции EXCEL как основа практических расчетов
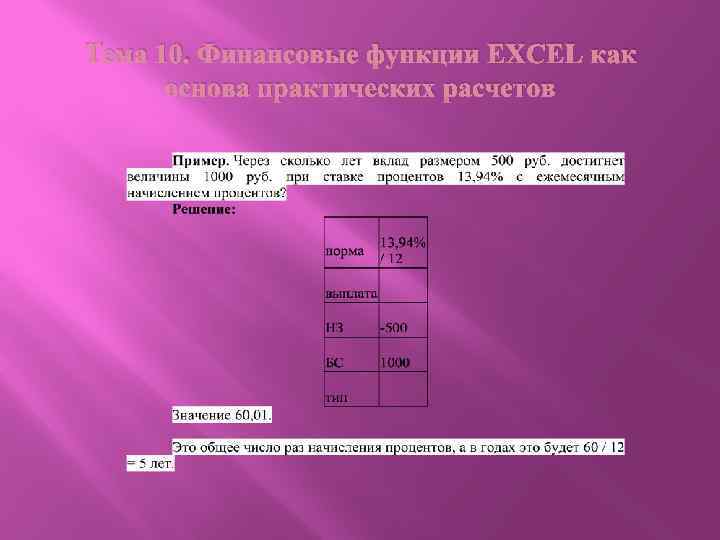
 Тема 10. Финансовые функции EXCEL как основа практических расчетов Определение срока финансовой операции Для определения срока финансовой операции используется функция КПЕР, которая вычисляет общее число периодов начисления процентов на основе постоянной процентной ставки. Данная функция используется как для единого платежа, так и для платежей, распределенных во времени. Аргументы функции: норма; выплата; НЗ; БС; тип.
Тема 10. Финансовые функции EXCEL как основа практических расчетов Определение срока финансовой операции Для определения срока финансовой операции используется функция КПЕР, которая вычисляет общее число периодов начисления процентов на основе постоянной процентной ставки. Данная функция используется как для единого платежа, так и для платежей, распределенных во времени. Аргументы функции: норма; выплата; НЗ; БС; тип.
 Тема 10. Финансовые функции EXCEL как основа практических расчетов
Тема 10. Финансовые функции EXCEL как основа практических расчетов
 Тема 10. Финансовые функции EXCEL как основа практических расчетов
Тема 10. Финансовые функции EXCEL как основа практических расчетов
 Тема 10. Финансовые функции EXCEL как основа практических расчетов Определение процентной ставки Для определения процентной ставки используется функция СТАВКА, которая определяет значение процентной ставки за один расчетный период. Для расчета годовой процентной ставки полученное значение необходимо умножить на число данных периодов в году. Аргументы функции: кпер; выплата; НЗ; БС; тип; предположение.
Тема 10. Финансовые функции EXCEL как основа практических расчетов Определение процентной ставки Для определения процентной ставки используется функция СТАВКА, которая определяет значение процентной ставки за один расчетный период. Для расчета годовой процентной ставки полученное значение необходимо умножить на число данных периодов в году. Аргументы функции: кпер; выплата; НЗ; БС; тип; предположение.
 Тема 10. Финансовые функции EXCEL как основа практических расчетов Пример. Предположим, что компании X потребуется 100 000 денежных единиц через 2 года. Компания готова вложить 5 000 денежных единиц сразу и по 2500 денежных единиц каждый последующий месяц. Каким должен быть процент на инвестированные средства, чтобы получить необходимую сумму в конце второго года? Решение. В этой задаче сумма 100 000 денежных единиц (аргумент бс функции СТАВКА) формируется за счет приведения к будущему моменту начального вклада размером 5 000 денежных единиц и фиксированных ежемесячных выплат. Поэтому среди аргументов функции СТАВКА следует указать оба аргумента: выплата = – 2 500, нз = – 5 000. Общее число периодов начисления процентов определяем исходя из таблицы 2: кпер = 2∙ 12. Подставив эти числа, получаем СТАВКА(24, 2 500, 5 000, 100 000) = 3, 28%. Годовая процентная ставка составит 3, 28%∙ 12 = 39, 36%.
Тема 10. Финансовые функции EXCEL как основа практических расчетов Пример. Предположим, что компании X потребуется 100 000 денежных единиц через 2 года. Компания готова вложить 5 000 денежных единиц сразу и по 2500 денежных единиц каждый последующий месяц. Каким должен быть процент на инвестированные средства, чтобы получить необходимую сумму в конце второго года? Решение. В этой задаче сумма 100 000 денежных единиц (аргумент бс функции СТАВКА) формируется за счет приведения к будущему моменту начального вклада размером 5 000 денежных единиц и фиксированных ежемесячных выплат. Поэтому среди аргументов функции СТАВКА следует указать оба аргумента: выплата = – 2 500, нз = – 5 000. Общее число периодов начисления процентов определяем исходя из таблицы 2: кпер = 2∙ 12. Подставив эти числа, получаем СТАВКА(24, 2 500, 5 000, 100 000) = 3, 28%. Годовая процентная ставка составит 3, 28%∙ 12 = 39, 36%.
 Тема 10. Финансовые функции EXCEL как основа практических расчетов 10. 2. Определение величины периодического платежа Для этого воспользуемся функцией ПЛТ(). Эта функция вычисляет величину выплаты за один период на основе фиксированных периодических выплат и постоянной процентной ставке. Эти выплаты включают в себя основные платежи и платежи по процентам. Будущая величина сделки на данном этапе анализа нам пока неизвестна. Однако она не является обязательным аргументом, поэтому мы можем ее опустить.
Тема 10. Финансовые функции EXCEL как основа практических расчетов 10. 2. Определение величины периодического платежа Для этого воспользуемся функцией ПЛТ(). Эта функция вычисляет величину выплаты за один период на основе фиксированных периодических выплат и постоянной процентной ставке. Эти выплаты включают в себя основные платежи и платежи по процентам. Будущая величина сделки на данном этапе анализа нам пока неизвестна. Однако она не является обязательным аргументом, поэтому мы можем ее опустить.
 Тема 10. Финансовые функции EXCEL как основа практических расчетов Пример 1. Банком выдан кредит в 10 000 денежных единиц на 5 лет под 15% годовых, начис ляемых дин раз в конце каждого о периода. По условиям договора кре дит олжен быть погашен д равными долями в течение указанного срока, выплачиваемыми в конце каждого периода. Разработать план погашения кредита для банка. Решение. Периодический платеж по данной операции составит: ПЛТ(0, 15; 5; – 10 000, 00)=2 983, 16. Теперь нетрудно определить будущее значение суммы, которую получит банк в результате проведения операции: ПЛТ (0, 15; 5; – 10 000, 00; ) ∙ 5=14 915, 80. Ответ. Периодический платеж для погашения кредита размером 10 000 денежных единиц составит 2 983, 16 денежной единицы.
Тема 10. Финансовые функции EXCEL как основа практических расчетов Пример 1. Банком выдан кредит в 10 000 денежных единиц на 5 лет под 15% годовых, начис ляемых дин раз в конце каждого о периода. По условиям договора кре дит олжен быть погашен д равными долями в течение указанного срока, выплачиваемыми в конце каждого периода. Разработать план погашения кредита для банка. Решение. Периодический платеж по данной операции составит: ПЛТ(0, 15; 5; – 10 000, 00)=2 983, 16. Теперь нетрудно определить будущее значение суммы, которую получит банк в результате проведения операции: ПЛТ (0, 15; 5; – 10 000, 00; ) ∙ 5=14 915, 80. Ответ. Периодический платеж для погашения кредита размером 10 000 денежных единиц составит 2 983, 16 денежной единицы.
 Тема 10. Финансовые функции EXCEL как основа практических расчетов Пример. Предположим, что необходимо накопить 4 000 денежных единиц за 3 года. Откладывая постоянно сумму в конце месяца, какой должна быть эта сумма, если процентная ставка составляет 12 % годовых. Решение. ПЛТ (0, 12/12; 3∙ 12; ; – 4000)=92, 86 (ден. ед. ). Ответ. Для того, что бы накопить 4 000 денежных единиц за три года при процентной ставке 12 % годовых, необходимо каждый месяц вносить 92, 86 денежных единиц.
Тема 10. Финансовые функции EXCEL как основа практических расчетов Пример. Предположим, что необходимо накопить 4 000 денежных единиц за 3 года. Откладывая постоянно сумму в конце месяца, какой должна быть эта сумма, если процентная ставка составляет 12 % годовых. Решение. ПЛТ (0, 12/12; 3∙ 12; ; – 4000)=92, 86 (ден. ед. ). Ответ. Для того, что бы накопить 4 000 денежных единиц за три года при процентной ставке 12 % годовых, необходимо каждый месяц вносить 92, 86 денежных единиц.
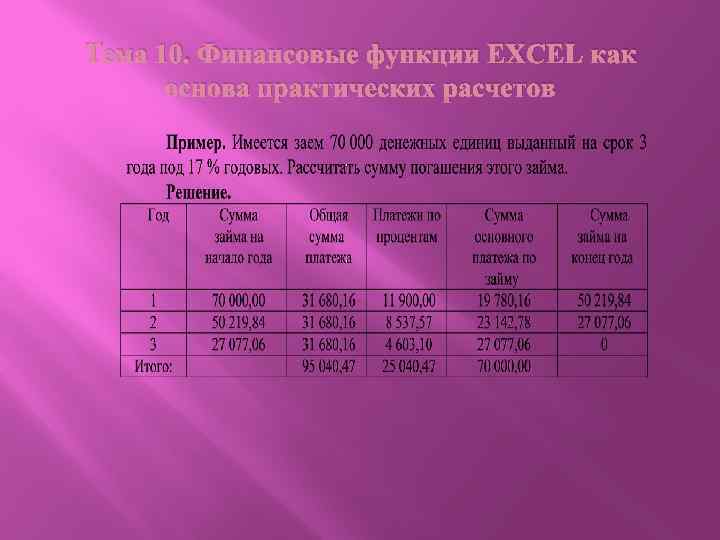
 Тема 10. Финансовые функции EXCEL как основа практических расчетов Пример. Имеется заем 70 000 денежных единиц выданный на срок 3 года под 17 % годовых. Рассчитать сумму погашения этого займа. Решение. Колонка общая сумма платежа заполняется с помощью функции ПЛТ. Для нашей задачи будем иметь ПЛТ (0, 17; 3; – 70000)=31 680, 16.
Тема 10. Финансовые функции EXCEL как основа практических расчетов Пример. Имеется заем 70 000 денежных единиц выданный на срок 3 года под 17 % годовых. Рассчитать сумму погашения этого займа. Решение. Колонка общая сумма платежа заполняется с помощью функции ПЛТ. Для нашей задачи будем иметь ПЛТ (0, 17; 3; – 70000)=31 680, 16.
 Тема 10. Финансовые функции EXCEL как основа практических расчетов 10. 3. Определение процентного дохода (выплаты) На практике как для банка, так и для заемщика большой интерес представляет та часть периодического платежа, которая составляет его процентный доход (выплату), а также его распределение во времени. Для банка эта часть периодического платежа составляет доход от операции, а для заемщика — сумму, вычитаемую из налогооблагаемой базы. Для осуществления подобных расчетов используются функции ПРОЦПЛАТ и ОСПЛТ, позволяющие выделить для заданного периода из платежа его процентную и основную части. Функция ПРОЦПЛАТ выделяет из периодического платежа его процентную часть: ПРОЦПЛАТ (ставка; период; кпер; пс)
Тема 10. Финансовые функции EXCEL как основа практических расчетов 10. 3. Определение процентного дохода (выплаты) На практике как для банка, так и для заемщика большой интерес представляет та часть периодического платежа, которая составляет его процентный доход (выплату), а также его распределение во времени. Для банка эта часть периодического платежа составляет доход от операции, а для заемщика — сумму, вычитаемую из налогооблагаемой базы. Для осуществления подобных расчетов используются функции ПРОЦПЛАТ и ОСПЛТ, позволяющие выделить для заданного периода из платежа его процентную и основную части. Функция ПРОЦПЛАТ выделяет из периодического платежа его процентную часть: ПРОЦПЛАТ (ставка; период; кпер; пс)
 Тема 10. Финансовые функции EXCEL как основа практических расчетов
Тема 10. Финансовые функции EXCEL как основа практических расчетов
 Тема 10. Финансовые функции EXCEL как основа практических расчетов Платежи по процентам рассчитываются с помощью функции ПРОЦПЛАТ. Эта функция вычисляет платежи по процентам за заданный период. Для примера 6. 2. получим: за 1 год ПРОЦПЛАТ (0, 17; 1; 3; – 70000)= 11 900, 00 (ден. ед. ), за 2 год ПРОЦПЛАТ (0, 17; 2; 3; – 70000)= 8 537, 57 (ден. ед. ), за 3 год ПРОЦПЛАТ (0, 17; 3; 3; – 70000)= 4 603, 10 (ден. ед. ).
Тема 10. Финансовые функции EXCEL как основа практических расчетов Платежи по процентам рассчитываются с помощью функции ПРОЦПЛАТ. Эта функция вычисляет платежи по процентам за заданный период. Для примера 6. 2. получим: за 1 год ПРОЦПЛАТ (0, 17; 1; 3; – 70000)= 11 900, 00 (ден. ед. ), за 2 год ПРОЦПЛАТ (0, 17; 2; 3; – 70000)= 8 537, 57 (ден. ед. ), за 3 год ПРОЦПЛАТ (0, 17; 3; 3; – 70000)= 4 603, 10 (ден. ед. ).
 Тема 10. Финансовые функции EXCEL как основа практических расчетов Сумма основного платежа по займу вычисляется с помощью функции ОСПЛТ. Для нашей задачи сумму основного платежа можно вычислить как разность между общей суммой платежа и платежами по процентам или с помощью функции ОСПЛТ. Для примера 2 получим: за 1 год ОСПЛТ (0, 17; 1; 3; – 70000)= 19 780, 1 (ден. ед. ), за 2 год ОСПЛТ (0, 17; 2; 3; – 70000)= 23 142, 78 (ден. ед. ), за 3 год ОСПЛТ (0, 17; 3; 3; – 70000)= 27 077, 06 (ден. ед. ).
Тема 10. Финансовые функции EXCEL как основа практических расчетов Сумма основного платежа по займу вычисляется с помощью функции ОСПЛТ. Для нашей задачи сумму основного платежа можно вычислить как разность между общей суммой платежа и платежами по процентам или с помощью функции ОСПЛТ. Для примера 2 получим: за 1 год ОСПЛТ (0, 17; 1; 3; – 70000)= 19 780, 1 (ден. ед. ), за 2 год ОСПЛТ (0, 17; 2; 3; – 70000)= 23 142, 78 (ден. ед. ), за 3 год ОСПЛТ (0, 17; 3; 3; – 70000)= 27 077, 06 (ден. ед. ).
 Тема 10. Финансовые функции EXCEL как основа практических расчетов 10. 4. Определение процентов и суммы погашения долга Функции этой ОБЩПЛАТ и ОБЩДОХОД предназначены для вычисления процентов и суммы погашенного долга между любыми двумя периодами выплат. Для этих функций необходимо указывать все аргументы, причем в виде положительных величин. Функция ОБЩПЛАТ служит для вычисления накопленной суммы процентов за период между двумя любыми выплатами. Определение данной величины играет важнейшую роль в бан ковском деле: ОБЩПЛАТ (ставка; кпер; нз; нач_период; кон_период; тип). Функция ОБЩДОХОД функция служит удобным инструментом для определения накопленной между двумя любыми периодами суммы, поступив шей в счет погашения основного долга по займу. Расчет данного показателя представляет интерес как для кредитных учреждений, так и для фирм, пользующихся заемными средствами: ОБЩДОХОД (ставка, количество периодов, нз, нач_период, кон_период, тип).
Тема 10. Финансовые функции EXCEL как основа практических расчетов 10. 4. Определение процентов и суммы погашения долга Функции этой ОБЩПЛАТ и ОБЩДОХОД предназначены для вычисления процентов и суммы погашенного долга между любыми двумя периодами выплат. Для этих функций необходимо указывать все аргументы, причем в виде положительных величин. Функция ОБЩПЛАТ служит для вычисления накопленной суммы процентов за период между двумя любыми выплатами. Определение данной величины играет важнейшую роль в бан ковском деле: ОБЩПЛАТ (ставка; кпер; нз; нач_период; кон_период; тип). Функция ОБЩДОХОД функция служит удобным инструментом для определения накопленной между двумя любыми периодами суммы, поступив шей в счет погашения основного долга по займу. Расчет данного показателя представляет интерес как для кредитных учреждений, так и для фирм, пользующихся заемными средствами: ОБЩДОХОД (ставка, количество периодов, нз, нач_период, кон_период, тип).
 Тема 10. Финансовые функции EXCEL как основа практических расчетов Пример. Пусть заем под недвижимость сделан на следующих условиях. Процентная ставка равна 9 % годовых, срок 30 лет, размер ссуды 125 000 денежных единиц. Проценты начисляются ежемесячно. Найти сумму выплат по процентам за первый месяц, за второй год. Решение. За первый месяц: ОБЩПЛАТ (0, 09/12; 30∙ 12; – 125000; 1 ; 1)= 937, 5 (ден. ед. ), За второй год: ОБЩПЛАТ (0, 09/12; 30∙ 12; – 125000; 13; 24)= 11 135, 23 (ден. ед. ). Почти аналогичный результат можно получить с помощью функции ПРПЛТ, но только за 1 ый месяц ПРПЛТ(0, 09/12; 1; 30∙ 12; – 125000)=937, 5 (ден. ед. ). Ответ. Сумма выплат по процентам за первый месяц составит 937, 5 денежных единиц, за второй год – 11 135, 23 денежных единиц.
Тема 10. Финансовые функции EXCEL как основа практических расчетов Пример. Пусть заем под недвижимость сделан на следующих условиях. Процентная ставка равна 9 % годовых, срок 30 лет, размер ссуды 125 000 денежных единиц. Проценты начисляются ежемесячно. Найти сумму выплат по процентам за первый месяц, за второй год. Решение. За первый месяц: ОБЩПЛАТ (0, 09/12; 30∙ 12; – 125000; 1 ; 1)= 937, 5 (ден. ед. ), За второй год: ОБЩПЛАТ (0, 09/12; 30∙ 12; – 125000; 13; 24)= 11 135, 23 (ден. ед. ). Почти аналогичный результат можно получить с помощью функции ПРПЛТ, но только за 1 ый месяц ПРПЛТ(0, 09/12; 1; 30∙ 12; – 125000)=937, 5 (ден. ед. ). Ответ. Сумма выплат по процентам за первый месяц составит 937, 5 денежных единиц, за второй год – 11 135, 23 денежных единиц.
 Тема 10. Финансовые функции EXCEL как основа практических расчетов Расчет суммы основных выплат по займу. Если займ погашается равными платежами в конце или начале каждого расчетного периода, между двумя периодами, то сумму основных выплат по займу можно найти с помощью функции ОБЩДОХОД.
Тема 10. Финансовые функции EXCEL как основа практических расчетов Расчет суммы основных выплат по займу. Если займ погашается равными платежами в конце или начале каждого расчетного периода, между двумя периодами, то сумму основных выплат по займу можно найти с помощью функции ОБЩДОХОД.
 Тема 10. Финансовые функции EXCEL как основа практических расчетов Пример. Допустим, выдана ссуда размером 1000 денежных единиц сроком на 6 месяцев, под 15% годовых, проценты начисляются ежеквартально. Определить величину основных выплат за 5 й год. Решение. ОБЩДОХОД(0, 15/4; 6∙ 4; – 1000; 17; 20)=201, 43 (ден. ед. ). Ответ. Величина основных выплат составит 201, 43 денежных единицы.
Тема 10. Финансовые функции EXCEL как основа практических расчетов Пример. Допустим, выдана ссуда размером 1000 денежных единиц сроком на 6 месяцев, под 15% годовых, проценты начисляются ежеквартально. Определить величину основных выплат за 5 й год. Решение. ОБЩДОХОД(0, 15/4; 6∙ 4; – 1000; 17; 20)=201, 43 (ден. ед. ). Ответ. Величина основных выплат составит 201, 43 денежных единицы.


