финансовая математика раздел количественного анализа финансовых операций

финансовая математика – раздел количественного анализа финансовых операций, предметом которого является изучение функциональных зависимостей между параметрами коммерческих сделок или финансово-банковских операций и разработка на их основе методов решения финансовых задач

Объектом изучения финансовой математики является финансовая операция, в которой необходимость использования финансовоэкономических вычислений возникает всякий раз, когда в условиях сделки (финансовой операции) прямо или косвенно присутствуют временные параметры: даты, сроки выплат, периодичность поступления денежных средств, отсрочка платежей и т. д

Фактор времени в финансовоэкономических расчетах • Важность учета фактора времени обусловлена принципом неравноценности денег, относящихся к различным моментам времени: – равные по абсолютной величине денежные суммы "сегодня" и "завтра" оцениваются по разному, – сегодняшние деньги ценнее будущих

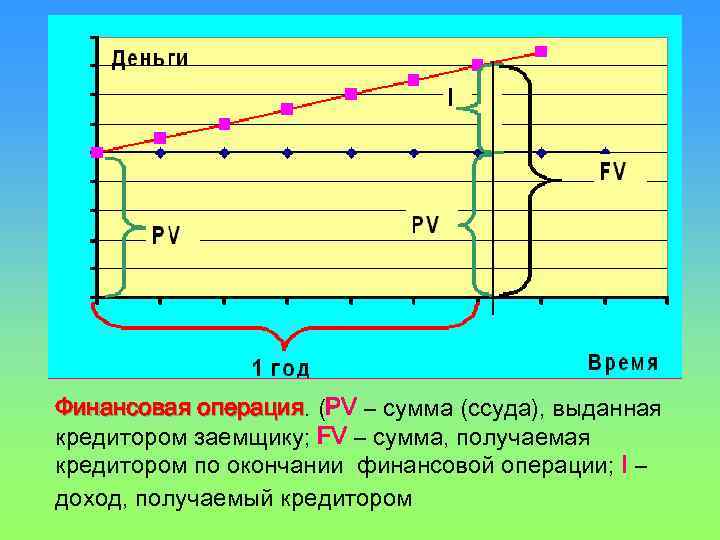Финансовая операция. (PV – сумма (ссуда), выданная операция кредитором заемщику; FV – сумма, получаемая кредитором по окончании финансовой операции; I – доход, получаемый кредитором

Начисление процентов, как правило, производится дискретно, т. е. за фиксированные одинаковые интервалы времени (периоды). "период начисления", – это отрезок времени между двумя следующими друг за другом процедурами взимания процентов. Обычные или декурсивные (postnumerando) проценты начисляются в конце периода. Как правило, в качестве единицы периода времени в финансовых расчетах принят год, однако это не исключает использования периода менее года.

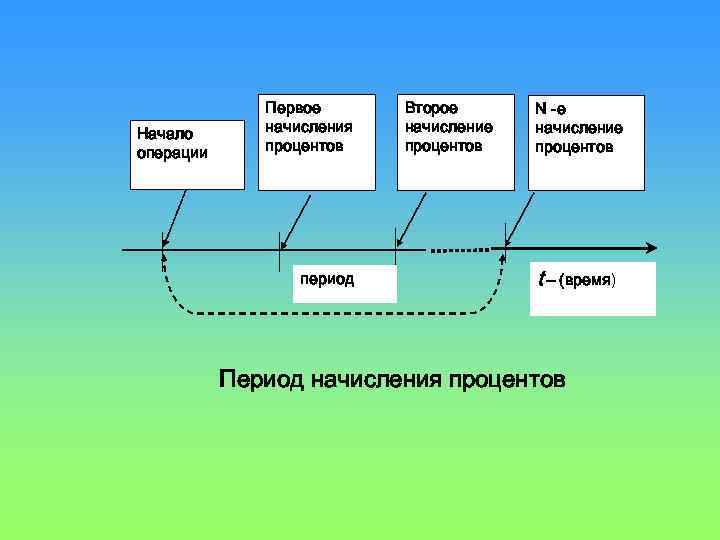Начало операции Первое начисления процентов период Второе начисление процентов N -e начисление процентов t – (время) Период начисления процентов

Как правило, в качестве единицы периода времени в финансовых расчетах принят год, однако это не исключает использования периода менее года. В любой простейшей финансовой операции всегда присутствуют четыре величины: vвремя (n) vсовременная величина (PV), vнаращенная или будущая величина (FV), vпроцентная ставка (r)

Основные термины и понятия Ø n – Срок погашения долга (англ. number of periods) – интервал времени, по истечении которого сумму долга и проценты нужно вернуть; Ø Если начисление процентов будет производиться m раз в год, а срок погашения долга – n лет, то общее количество периодов начисления за весь срок финансовой операции составит: N=n • m

Основные термины и понятия Ø PV – текущая стоимость (англ. present value) – исходная сумма или оценка современной величины денежной суммы, поступление которой ожидается в будущем, в пересчете на более ранний момент времени; Ø FV – будущая стоимость (англ. future value) – наращенная сумма или будущая стоимость т. е. первоначальная сумма долга с начисленными на нее процентами к концу срока ссуды; Ø I – Процентные деньги (англ. interest money), называемые часто коротко "проценты", представляют собой абсолютный доход от предоставления долга. I= FV-PV Ø Это абсолютные показатели

относительные показатели r – процентная ставка (rate of interest ): Ø характеризует интенсивность начисления процентов за единицу времени, Ø отношение суммы процентных денег, выплачивающихся за определенный период времени, к величине ссуды. Этот показатель выражается либо в долях единицы, либо в процентах. • r =I/PV = (FV – PV) / PV В литературе достаточно часто этот показатель называется коэффициентом или множителем наращения, показывающим во сколько раз наращенная сумма больше первоначальной суммы долга и по существу может приниматься как базисный темп роста. ; Ø

относительные показатели Если соотнести величину процентных денег (FV – PV) не с PV, а с будущей стоимостью FV, наращенной по мере присоединения процентов, то получим другую меру эффективности – темп снижения d = (FV – PV) / FV, называемый учетной ставкой (англ. discount rate), или дисконтным множителем (нормой банковского дисконтирования) Примечание Термин дисконтирование в широком смысле означает определение значения стоимостной величины на некоторый момент времени при условии, что в будущем она составит заданную величину. Именно дисконтирование позволяет учитывать в стоимостных расчетах фактор времени, поскольку дает сегодняшнюю оценку суммы, которая будет получена в будущем. Привести стоимость денег можно к любому моменту времени, а не обязательно к началу финансовой операции.

относительные показатели дисконтирование – приведение будущих денег к текущему моменту времени, а дисконтный множитель (d) -показывает, какую долю составляет первоначальная сумма долга в величине наращенной суммы. d = (FV – PV) / FV

Различие в ставке процентов и учетной ставке заключается в различии базы для начислений процентов Ø в процентной ставке в качестве базы берется первоначальная сумма долга: Ø r = (FV - PV) / PV Ø в учетной ставке за базу принимается наращенная сумма долга: d = (FV - PV) / FV

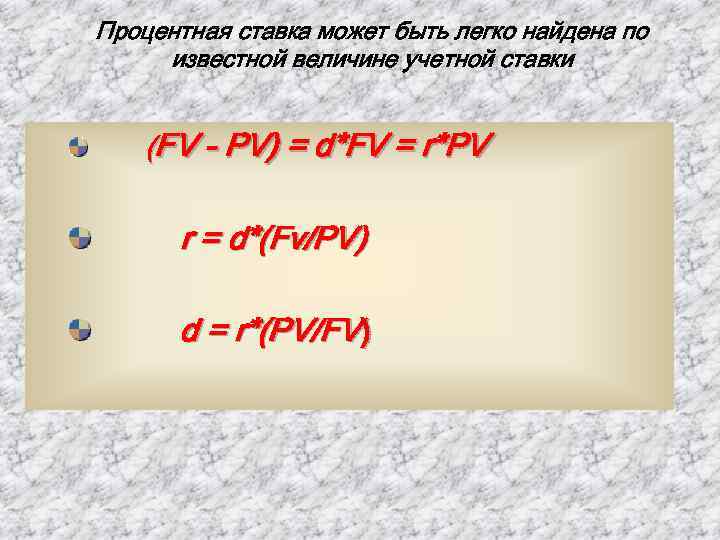Процентная ставка может быть легко найдена по известной величине учетной ставки (FV - PV) = d*FV = r*PV r = d*(Fv/PV) d = r*(PV/FV)

Пример 1 Вы заняли сегодня 100 руб. , дав обязательство вернуть к указанной дате 120 руб. Оценить доходность этой сделки для кредитора величинами процентной (r) и учетной (d) ставок, приняв весь период между двумя моментами времени за полный срок договора, приняв его за единицу времени n=1. Решение PV = 100 руб. , FV = 120 руб. , I =(FV – PV) = (120 – 100) = 20 руб. , r = 20/100 = 20%, d= 20/120 = 16. 67%.

Пример 2 Вы обратились к кредитору с просьбой о займе 100 руб. (PV) на срок 1 год (n=1). Какую сумму сможет получить кредитор по окончании срока займа, при процентной и учетной ставке =20%? Решение FVпроц = PV* (1+r) FVучетн = PV/(1 -d) r =d =0. 2 FVпроц =100 руб. *(1+0. 2) =120 руб. FVучетн =100 руб. /(1 -0. 2) = 125 руб.

Изменение СТОИМОСТИ ВЛОЖЕНИЙ ЗА СЧЕТ ПРИСОЕДИНЕНИЯ ПРОЦЕНТОВ Экономический смысл операции наращения состоит в определении величины той суммы, которой будет или желает располагать инвестор по окончании этой операции Величина FV показывает будущую стоимость "сегодняшней" величины инвестиции PV при заданном уровне интенсивности начисления процентов r

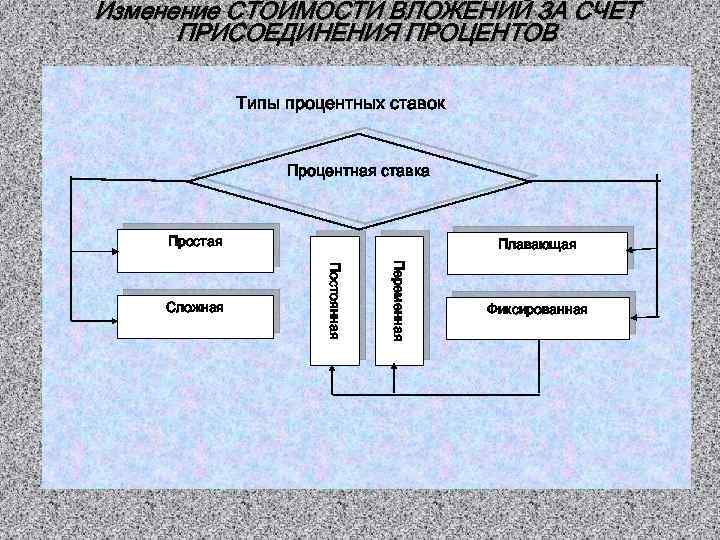Изменение СТОИМОСТИ ВЛОЖЕНИЙ ЗА СЧЕТ ПРИСОЕДИНЕНИЯ ПРОЦЕНТОВ Типы процентных ставок Процентная ставка Простая Переменная Постоянная Сложная Плавающая Фиксированная

Типы процентных ставок применяется к одной и той же Простая процентная первоначальной сумме долга на ставка протяжении всего срока ссуды, т. е. исходная база (денежная сумма) всегда одна и та же. Сложная процентная ставка Фиксированная процентная ставка применяется к наращенной сумме долга, т. е. к сумме, увеличенной на величину начисленных за предыдущий период процентов, – таким образом, исходная база постоянно увеличивается. ставка, зафиксированная в виде определенного числа (суммы) в финансовых контрактах.

Типы процентных ставок Плавающая процентная ставка привязанная к определенной величине, изменяющейся во времени, включая надбавку к ней (маржу), которая определяется целым рядом условий (сроком операции и т. п. ). Основу процентной ставки составляет базовая ставка, которая является начальной величиной. Постоянная процентная ставка неизменная на протяжении всего периода ссуды. Переменная процентная ставка дискретно изменяющаяся во времени, но имеющая конкретную числовую характеристику.

Простые проценты Модель простых процентов предусматривает накопление наращенной суммы FV (общей суммы долга) за счет периодического (например, ежегодного) начисления процентных денег (I) В соответствии с этим наращенная сумма равна: üк концу первого года – FV 1 = PV+I üк концу второго года – FV 2 = PV+2*I üк концу n-го года – FVn= PV+n*I _____________________________ Напомним, что «процентные деньги» – это разность между первоначальной денежной суммой (PV) и наращенной денежной сумой (FV) I =FV – PV.

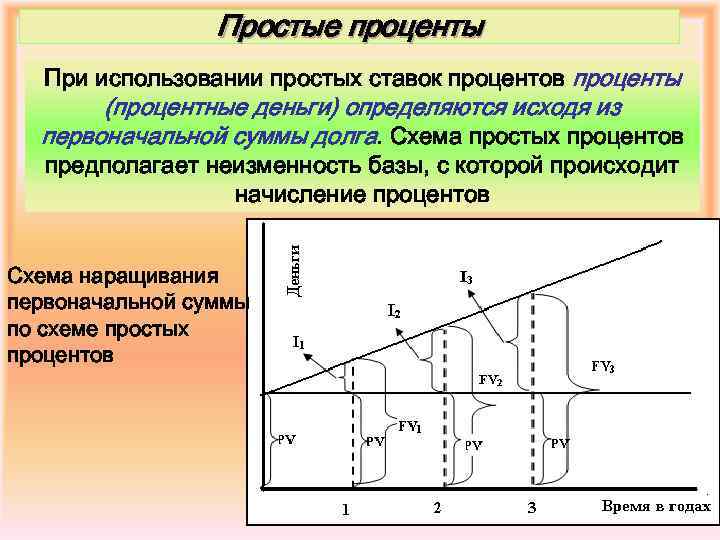Простые проценты При использовании простых ставок процентов проценты (процентные деньги) определяются исходя из первоначальной суммы долга. Схема простых процентов предполагает неизменность базы, с которой происходит начисление процентов Схема наращивания первоначальной суммы по схеме простых процентов

Простые проценты В общем случае, модель накопления капитала по схеме простых процентов принимает вид: FV = PV + I = PV + n*I = = PV* (1 + r *n ) = PV * kн Где I –процентные деньги 1 периода начисления, kн = (1 + r *n) – коэффициент (множитель) наращения простых процентов, показывающий будущую стоимость одной денежной единицы, вложенной сроком на n периодов при начислении в конце каждого из них процентного дохода по ставке r без капитализации начисленных ранее процентов.

Простые проценты Временная база финансовой операции В тех случаях, когда срок ссуды менее года, происходит модификация формулы: а) если срок ссуды выражен в месяцах ( М ), то величина n выражается в виде дроби: n = М / 12, б) если время выражено в днях (t), то величина n выражается в виде дроби: n = t / T, где: t – число дней ссуды, т. е. продолжительность срока, на который выдана ссуда; T – расчетное число дней в году (временная база).

Простые проценты Временная база финансовой операции Временную базу ( T ) можно представить: Øусловно состоящую из 360 дней В этом случае речь идет об обыкновенном (ordinary interest), или коммерческом проценте; ØИспользовать действительное число дней в году (365 или 366 дней). В этом случае получают точный процент (exact interest).

Простые проценты Временная база финансовой операции Число дней ссуды ( t ) можно определять: Øусловно, исходя из того, что продолжительность любого целого месяца составляет 30 дней, а оставшиеся дни от месяца считают точно, – в результате получают так называемое приближенное число дней ссуды; Øиспользуя прямой счет или специальные таблицы порядковых номеров дней года, рассчитывают фактическое число дней между датами, – в этом случае получают точное число дней ссуды

Простые проценты Временная база финансовой операции ð «германская практика расчета» -обыкновенные проценты с приближенным числом дней ссуды, или, как часто называют, когда продолжительность года условно принимается за 360 дней, а целого месяца – за 30 дней[1]. ð «французская практика расчета» - обыкновенные проценты с точным числом дней ссуды, или когда продолжительность года условно принимается за 360 дней, а продолжительность ссуды рассчитывается точно по календарю[2]. . _____________________________ [1] Этот способ обычно используется в Германии, Дании, Швеции [2] Этот способ имеет распространение во Франции, Бельгии, Испании, Швейцарии

Простые проценты Временная база финансовой операции «английская практика расчета» - точные проценты с точным числом дней ссуды, или когда продолжительность года и продолжительность ссуды берутся точно по календарю[3]. ____________________________ [3] Этот способ применяется в Португалии, Англии, США.

Пример Простые проценты Сумма в размере 2000 рублей дана в долг на 1 год по схеме простого процента под 10% годовых. Определить проценты и сумму, подлежащую возврату. Решение: ØНаращенная сумма: FV = PV (1 + n *r ) = 2000 (1 + 1 * 0. 1) = 2200 руб. или FV = PV * kн = 2000 * 1, 1 = 2200 руб. ØСумма начисленных процентов: I = PV * n * r = 2000 * 1 * 0, 1 = 200 руб. или I = FV - PV = 2200 - 2000 = 200 руб.

Пример Простые проценты Ссуда выдана под 10% годовых сроком: а) на 5 месяцев; б) на 3 месяца. Определить процентную ставку за срок ссуды. Решение: а) n = 5/12 =0. 42; r 5 мес = 0, 1 * 5/12 = 0. 0417; б) n = 3/12 =0, 25; m = 4; r =0, 1/4 = 0, 025

Простые проценты Переменная ставка В том случае, если на последовательных интервалах начисления процентов n 1, n 2, n 3, …, nm устанавливаются разные процентные ставки r 1, r 2, r 3, …, rm , то наращенная сумма может быть определена как: FV=PV *(1 + nk*rk) = PV*kn где коэффициент наращения (kn ) kn = (1 + nk*rk)

Простые проценты Определение срока ссуды и величины процентной ставки Срок финансовой операции может быть определен как: Øпри определении срока в годах n = (FV - PV) / (PV *r) Øпри определении срока в днях t = [(FV - PV) / (PV * r)] * T. Процентная ставка может быть определена как: r = (FV - PV) / (PV * n) = [(FV - PV) / (PV * t)] * T.

Простые проценты Пример Клиент внес вклад в банк в сумме 1 тыс. руб. сроком на 1 год. Процентная ставка до середины второго квартала составляла 30 % годовых, далее до конца третьего квартала - 25 %, а с начала четвертого квартала - снова 30%. Какую сумму клиент получил в конце года? Решение: Периоды; Øс начала года до середины второго квартала (n 1) равен 4, 5 месяца, или 0, 375 года; Øсередины второго квартала до конца третьего (n 2) равен 4, 5 месяца, или 0, 375 года; Øконца третьего квартала до конца четвертого (n 3) равен 3 месяца, или 0, 25 года

Простые проценты Пример Решение: Коэффициент наращения: Ø за период до середины второго квартала – k 1 = 0, 3 * 0, 375 = 0, 113, Ø от середины второго квартала до начала четвертого квартала – k 2 = 0, 25*0, 375 =0, 094. ; Ø за четвертый квартал k 3=0, 3 * 0, 25 = 0, 075 Ø за год Ø k год = k 1 + k 2 + k 3 =0, 281 В результате в конце года клиент получит сумму: FV = PV *(1+ k год ) = 1281, 25 руб

Простые проценты Определение срока ссуды и величины процентной ставки Срок финансовой операции может быть определен как: Øпри определении срока в годах n = (FV - PV) / (PV *r) Øпри определении срока в днях t = [(FV - PV) / (PV * r)] * T. Процентная ставка может быть определена как: r = (FV - PV) / (PV * n) = [(FV - PV) / (PV * t)] * T.

Простые проценты Определение срока ссуды и величины процентной ставки Пример. За какое время может быть накоплена сумма в 2000 долларов, если сегодня мы можем оформить депозитный вклад 1000 долларов под 8% годовых? Решение n = (FV - PV) / (PV *r)= (2000 -1000)/(1000*. 08) = 12. 5 года Пример. В контракте предусматривается погашение обязательств через 120 дней в сумме 1200 долларов, при первоначальной сумме долга 1150 долларов. Определить доходность операции для кредитора в виде обыкновенной (коммерческой) процентной ставки. Решение r = [(FV - PV) / (PV * t)] *T =

Сложные проценты В финансовой практике основная часть расчетов ведется с использованием схемы сложных процентов. Применение схемы сложных процентов целесообразно в тех случаях, когда: Øпроценты не выплачиваются по мере их начисления, а присоединяются к первоначальной сумме долга; Ø срок ссуды больше одного года. Присоединение начисленных процентов к сумме долга, которая служит базой для их начисления, называется капитализацией процентов;

Сложные проценты ØЗа первый период начисления FV 1 = PV +I = PV+PV *r = PV*(1+ r); ØЗа два периода начисления при условии капитализации ранее наращенной суммы FV 2 = FV 1 *(1+r)=PV*(1+ r)2 ……. Øза n периодов начисления формула примет вид: вид FV = PV • (1 + r)n = PV • kн , где: FV – наращенная сумма долга; PV – первоначальная сумма долга; r – ставка процентов в периоде начисления; n – количество периодов начисления; kн – коэффициент (множитель) наращения сложных процентов

Сложные проценты Примечание Как и в случае простых процентов, множитель наращения показывает будущую стоимость 1 денежной единицы, вложенной на n периодов. Для обозначения этого финансового коэффициента часто используется стандартная аббревиатура FVIF (от англ. Future Value Interest Factor – процентный множитель будущей стоимости). Будущая стоимость определяется умножением размера первоначально инвестированной суммы на этот коэффициент: FV =PV*FVIF (n, r)

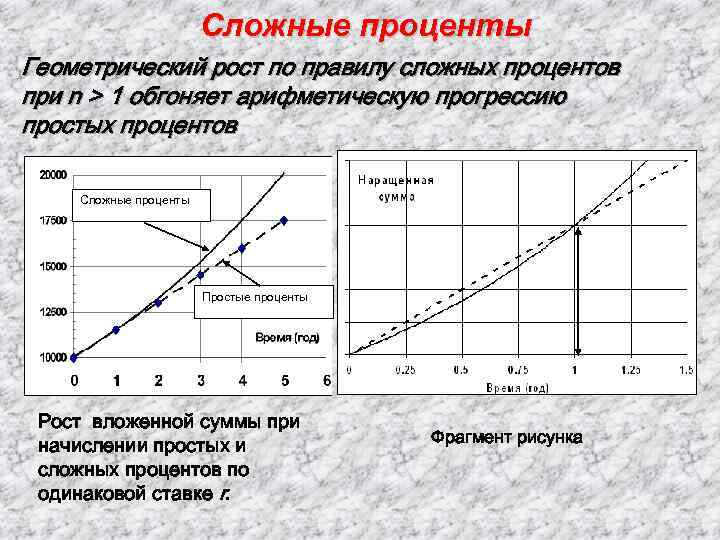Сложные проценты Геометрический рост по правилу сложных процентов при n > 1 обгоняет арифметическую прогрессию простых процентов Сложные проценты Простые проценты Рост вложенной суммы при начислении простых и сложных процентов по одинаковой ставке r. Фрагмент рисунка

Сложные проценты Геометрический рост по правилу сложных процентов при n > 1 обгоняет арифметическую прогрессию простых процентов При краткосрочных ссудах (менее одного года) начисление по простым процентам предпочтительнее, чем по сложным процентам; при сроке в один год разница отсутствует, но при среднесрочных и долгосрочных ссудах наращенная сумма, рассчитанная по сложным процентам значительно выше, чем по простым. При любом r, üесли 0 < n < 1, то (1 + n*r) > (1 +r)n; üесли n = 1, то (1 +n*r) = (1 + r)n. üесли n > 1, то (1 + n*r) < (1 + r)n;

Сложные проценты Таким образом, для лиц, предоставляющих кредит: üболее выгодна схема простых процентов, если срок ссуды менее года (проценты начисляются однократно в конце года); üболее выгодной является схема сложных процентов, если срок ссуды превышает один год; üобе схемы дают одинаковый результат при продолжительности периода один год и однократном начислении процентов

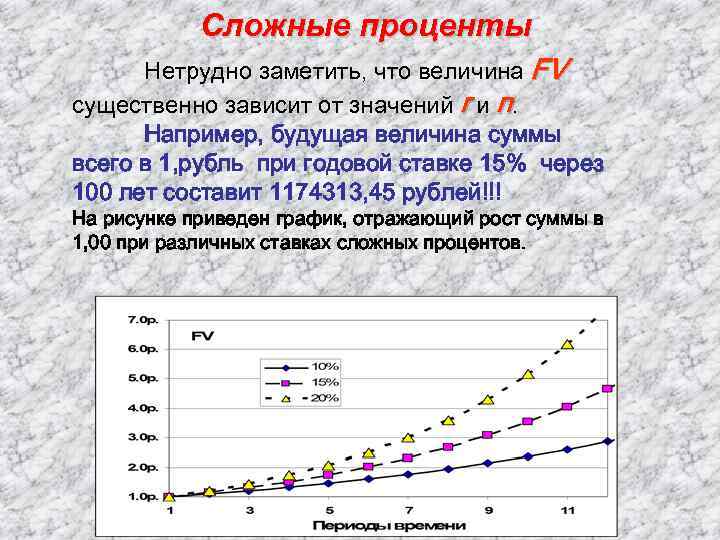Сложные проценты Нетрудно заметить, что величина FV существенно зависит от значений r и n. Например, будущая величина суммы всего в 1, рубль при годовой ставке 15% через 100 лет составит 1174313, 45 рублей!!! На рисунке приведен график, отражающий рост суммы в 1, 00 при различных ставках сложных процентов.

Сложные проценты Начисление процентов при дробных периодах В случае, когда срок финансовой операции выражен дробным числом лет, начисление процентов возможно с использованием двух методов: общий метод заключается в прямом расчете по формуле сложных процентов: FV = PV * (1 + r)n, n = a + b, где n – период сделки; a – целое число лет; b – дробная часть года. В банке получен кредит под 9, 5% годовых в размере 250 тыс. долларов со сроком погашения через два года и 9 месяцев. Определить сумму, которую необходимо вернуть по истечении срока займа, учитывая, что банк использует германскую практику начисления процентов. Решение FV = PV *(1 + r)n = 250 * (1 + 0, 095)2, 9 = 320, 87 тыс. долларов

Сложные проценты Начисление процентов при дробных периодах смешанный метод расчета предполагает для целого числа лет периода начисления процентов использовать формулу сложных процентов, а для дробной части года – формулу простых процентов: FV = PV * (1 + r)a * (1 + b*r). В банке получен кредит под 9, 5% годовых в размере 250 тыс. долларов со сроком погашения через два года и 9 месяцев. Определить сумму, которую необходимо вернуть по истечении срока займа, учитывая, что банк использует германскую практику начисления процентов. Решение FV = PV * (1 + r) a * (1 + b*r) = = 250 *(1 + 0, 095)2 * (1 + 270/360 * 0, 095) = 321, 11 тыс. долларов Таким образом, смешанная схема для кредитора оказывается более выгодной!

Сложные проценты Переменная ставка процентов При предоставлении долгосрочных ссуд, часто используются изменяющиеся во времени, но заранее зафиксированные для каждого периода ставки сложных процентов. В случае использования переменных процентных ставок, формула наращения имеет следующий вид: вид FV = PV*(1+ r 1)n 1 * (1+ r 2)n 2 *…(1+ rk)nk =PV* где rk – последовательные во времени значения процентных ставок; nk – длительность периодов, в течение которых используются соответствующие ставки

Сложные проценты Переменная ставка процентов Пример Фирма получила кредит в банке на сумму 250000 долларов сроком на 5 лет. Процентная ставка по кредиту определена: Øдля первого года – в 10% для 1 -го года, Øдля 2 -го года предусмотрена надбавка к процентной ставке в размере 1, 5%, Øдля последующих лет предусмотрена надбавка к процентной ставке в размере 1%. Определить сумму долга, r подлежащую )погашению в конце срока FV = PV*(1+ r 1)n * 1+ 2)n *…(1+ rk n =PV* займа Решение FV = PV *(1 + r 1)n 1 * (1 + r 2)n 2 * … * (1 + rk)nk = =250000 * (1 + 0, 1) * (1 + 0, 115) * (1 + 0, 125)3 = =436581. 3 доллара Таким образом, сумма, подлежащая погашению в конце срока займа, составит 436581. 3 доллара, из которых 250000 долларов являются непосредственно суммой долга, а 186581. 3 доллара – проценты по долгу.

Сложные проценты Номинальная ставка (nominal rate) – годовая ставка процентов, исходя из которой определяется величина ставки процентов в каждом периоде начисления, при начислении сложных процентов несколько раз в год. Если начисление процентов будет производиться m раз в год, а срок долга – n лет, то общее количество периодов начисления за весь срок финансовой операции составит N=n • m Отсюда формулу сложных процентов можно записать в следующем виде: FV = PV • (1 + rn / m)N = P V • (1 + rn /m)mn , где rn – номинальная годовая ставка процентов.

Сложные проценты Эффективная ставка В банковской практике часто используется понятие эффективной ставки Эффективная ставка (effective percentage rate – EPR) – характеризует процентный доход, получаемый инвестором за один год в результате вложения одной денежной единицы по номинальной годовой ставке сложных процентов r при частоте начисления m раз в год. Т. е. , эффективная ставка показывает, какая годовая ставка сложных процентов дает тот же финансовый результат, что и mразовое наращение в год по ставке rn/ m: (1 + ref ) n = (1 + rn / m) m • n, следовательно, ref= (1 + rn / m) m - 1.

Сложные проценты Эффективная ставка Расчет эффективной ставки является мощным инструментом финансового анализа, так как ее значение позволяет сравнивать между собой финансовые операции, имеющие различные условия: условия чем выше эффективная ставка финансовой операции, тем (при прочих равных условиях) она выгоднее для кредитора

Сложные проценты Эффективная ставка Рассчитаем эффективную ставку для финансовой операции, с номинальной ставкой 10%, для ежеквартального и ежемесячного начисления процентов Решение: Решение ØЭффективная ставка ежеквартального начисления процентов, исходя из 10% годовых, составит: ref= (1 + rn/ m)m - 1 = (1 + 0, 1 / 4)4 - 1 = 0, 1038 ØЭффективная ставка ежемесячного начисления процентов будет равна: ref= (1 + rn/ m)m - 1 = (1 + 0, 1 / 12)12 - 1 = 0, 1047 Таким образом, годовая ставка, эквивалентная номинальной ставке процентов в размере 10% годовых при ежемесячном начислении процентов, составит 10, 47% против 10, 38% с ежеквартальным начислением процентов. Чем больше периодов начисления, тем быстрее идет процесс наращения.

Сложные проценты Непрерывное начисление процентов В современных условиях в связи с развитием систем электронных платежей проценты могут начисляться чаще, чем один раз в день. При бесконечно частом ( ) дроблении года на малые процентные периоды, то есть при непрерывном наращении сложных процентов получается показательный закон роста). e r*n В этом случае наращенная сумма FV может быть записана как: Где ks –коэффициент наращения при непрерывном начислении процентов по номинальной годовой ставке r.

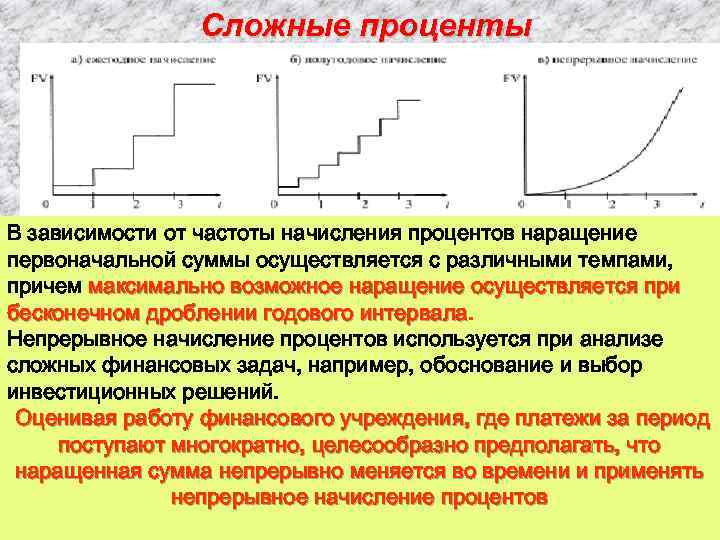Сложные проценты В зависимости от частоты начисления процентов наращение первоначальной суммы осуществляется с различными темпами, причем максимально возможное наращение осуществляется при бесконечном дроблении годового интервала Непрерывное начисление процентов используется при анализе сложных финансовых задач, например, обоснование и выбор инвестиционных решений. Оценивая работу финансового учреждения, где платежи за период поступают многократно, целесообразно предполагать, что наращенная сумма непрерывно меняется во времени и применять непрерывное начисление процентов

Дисконтированиее В практике финансовых расчетов часто приходится решать задачи, обратные определению наращенной суммы: по уже известной наращенной сумме (FV) следует определить неизвестную первоначальную сумму долга (PV). Наиболее часто такие ситуации возникают при разработке условий финансовой сделки, когда проценты с наращенной суммы удерживаются непосредственно при выдаче ссуды. Процесс начисления и удержания процентов вперед, до наступления срока погашения долга, называют учетом, а сами проценты в виде разности наращенной и первоначальной сумм долга дисконтом (discount). В литературе, посвященной финансовому анализу, такой расчет часто называют приведением стоимостного показателя к заданному моменту времени, а величину PV называют приведенной (современной или текущей) величиной FV

Дисконтированиее Математическое дисконтирование связано с определением так называемого современного, или приведенного, значения PV на некоторый момент времени, которое соответствует заданному значению FV в другой момент времени. Простейшая задача - определение суммы вклада PV на основе заданной конечной величины в будущем FV через временной период начислений n под заданную. например, простую ставку процентов: где kd – дисконтный множитель (коэффициент приведения) для простых процентов. Дисконтный множитель показывает, какую долю составляет первоначальная сумма долга в величине наращенной суммы. kd = 1/(1 + n*r).

Дисконтированиее Математическое дисконтирование Дисконтированное значение будущей суммы вклада по простой ставке процентов равно: kd = 1/(1 + n*r). Дисконтированное значение будущей суммы вклада по сложной ставке процентов равно (при начислении процнтов m раз в год): kd =

Дисконтированиее Математическое дисконтирование Пример. Вы решили через 2 года приобрести автомобиль стоимостью 200000 руб. С этой целью Вы намерены сегодня воспользоваться услугами банка, размещаете депозит под 10% годовых с капитализацией процентов: а) ежегодно; б) ежемесячно. Какая сумма должна быть положена в банк? Решение. а) б) 200000/(1+0. 1/1)^2 = 165289. 3 руб 200000/(1+0. 1/12)^24 =163881. 9 руб.

Дисконтированиее Банковский учет заключается в покупке денежных обязательств, (например, векселя ) банком по цене, которая меньше номинальной указанной в ней суммы. В этом случае говорят, что вексель учитывается и клиент получает сумму: PV = FV -D простая учетная ставка (d): D = FV - PV = FV * n * d = FV * t / T * d , где n – продолжительность срока в годах от момента учета до даты выплаты известной суммы в будущем. Отсюда: PV = FV - FV * n * d = FV * (1 - n * d) = FV*кd где kd = (1 - n * d) – дисконтный множитель Дисконтирование по простой учетной ставке чаще всего производится по французской практике начисления процентов, т. е. когда временная база принимается за 360 дней, а число дней в периоде берется точным.

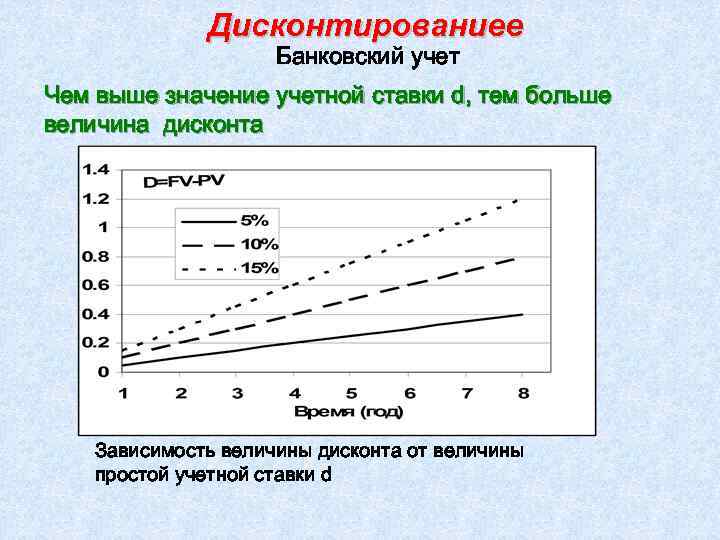Дисконтированиее Банковский учет Чем выше значение учетной ставки d, тем больше величина дисконта Зависимость величины дисконта от величины простой учетной ставки d

Дисконтированиее Банковский учет Вексель выдан на 5000 руб. с уплатой 17 ноября, а владелец учел его в банке 19 августа по учетной ставке 8%. Определить сумму, полученную предъявителем векселя и доход банка при реализации дисконта Решение: ØДля определения суммы при учете векселя рассчитываем число дней, оставшихся до погашения обязательств: t = 13 (август) + 30 (сентябрь) + 31 (октябрь) + 17 (ноябрь) - 1 = 90 дней. Отсюда, определяемая сумма: PV = FV * (1 - t / T *d) = 5000 (1 - 90 / 360 * 0, 08) = 4900 руб. Тогда дисконт составит: D = FV - PV = 5000 - 4900 = 100 руб. Следовательно, предъявитель векселя получит сумму 4900 руб. , а банк при наступлении срока векселя получит дисконт в размере 100 руб

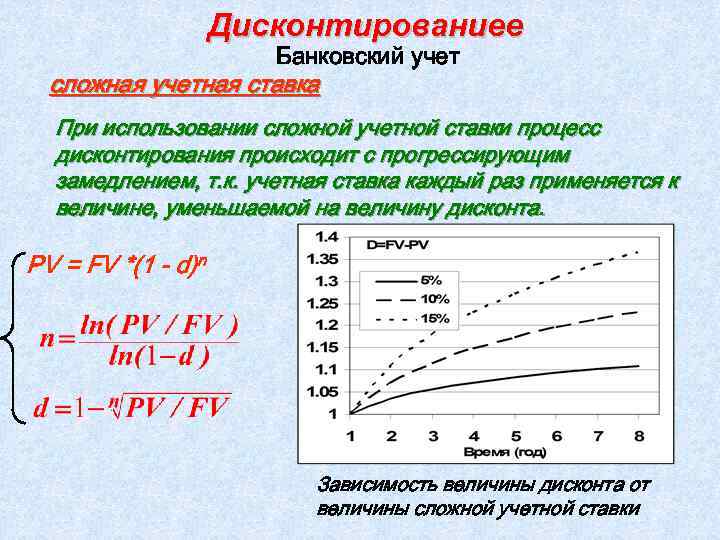Дисконтированиее Банковский учет сложная учетная ставка При использовании сложной учетной ставки процесс дисконтирования происходит с прогрессирующим замедлением, т. к. учетная ставка каждый раз применяется к величине, уменьшаемой на величину дисконта. PV = FV *(1 - d)n Зависимость величины дисконта от величины сложной учетной ставки

Дисконтированиее Банковский учет сложная учетная ставка Пример Вексель на сумму 100 тыс. руб. и сроком платежа через 3 года продан с дисконтом по сложной учетной ставке 30% годовых. Какова сумма дисконта и современная величина платежа? PV = FV*(1 -d)n = 100000*(1 -0. 3)3 = 34300 руб. D =FV-PV = 100000 – 34300 = 65700 руб.

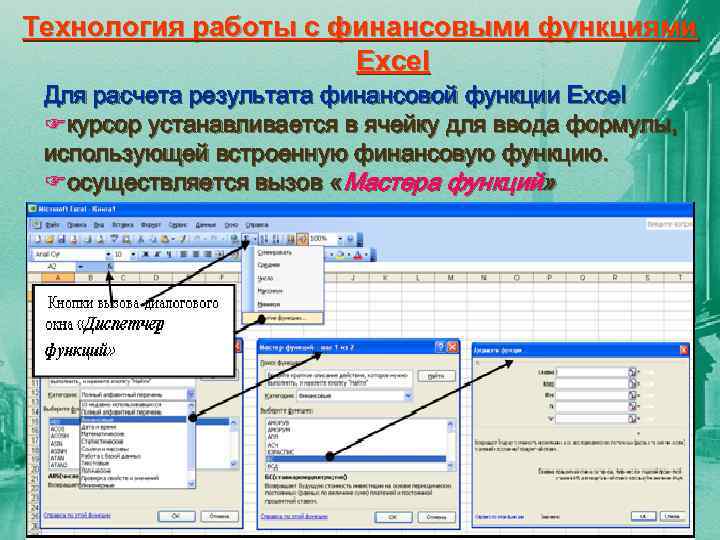Технология работы с финансовыми функциями Excel Для расчета результата финансовой функции Excel Fкурсор устанавливается в ячейку для ввода формулы, использующей встроенную финансовую функцию. Fосуществляется вызов «Мастера функций»

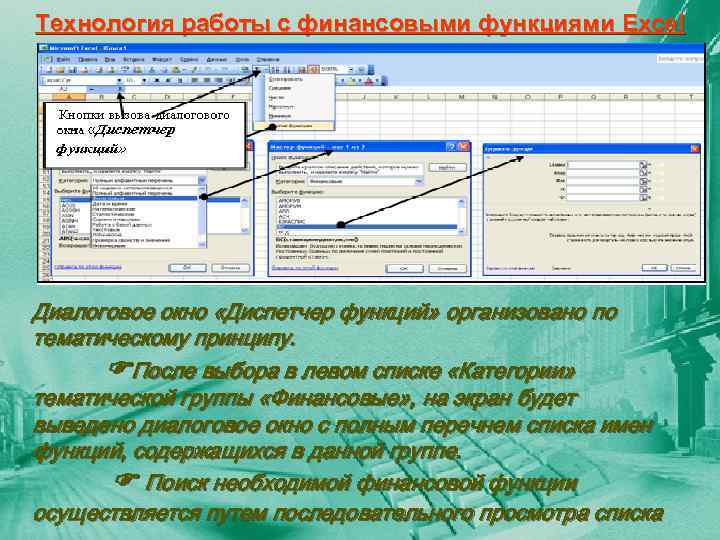Технология работы с финансовыми функциями Excel Диалоговое окно «Диспетчер функций» организовано по тематическому принципу. После выбора в левом списке «Категории» тематической группы «Финансовые» , на экран будет выведено диалоговое окно с полным перечнем списка имен функций, содержащихся в данной группе. Поиск необходимой финансовой функции осуществляется путем последовательного просмотра списка

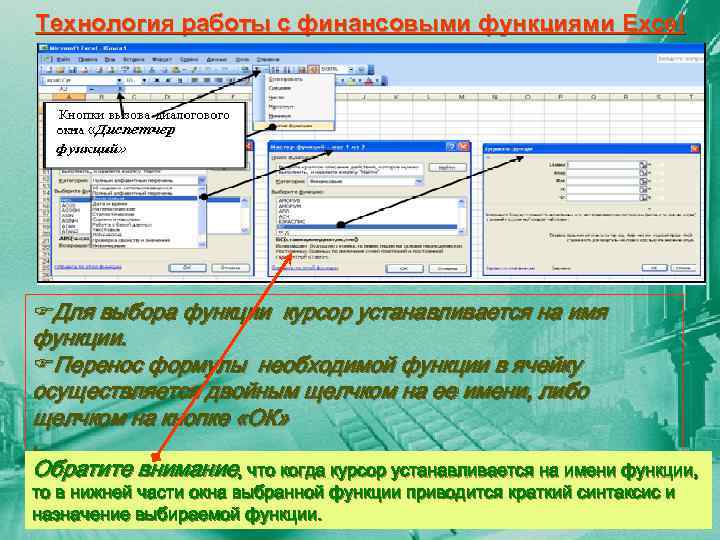Технология работы с финансовыми функциями Excel FДля выбора функции курсор устанавливается на имя функции. FПеренос формулы необходимой функции в ячейку осуществляется двойным щелчком на ее имени, либо щелчком на кнопке «ОК» , Обратите внимание, что когда курсор устанавливается на имени функции, то в нижней части окна выбранной функции приводится краткий синтаксис и назначение выбираемой функции.

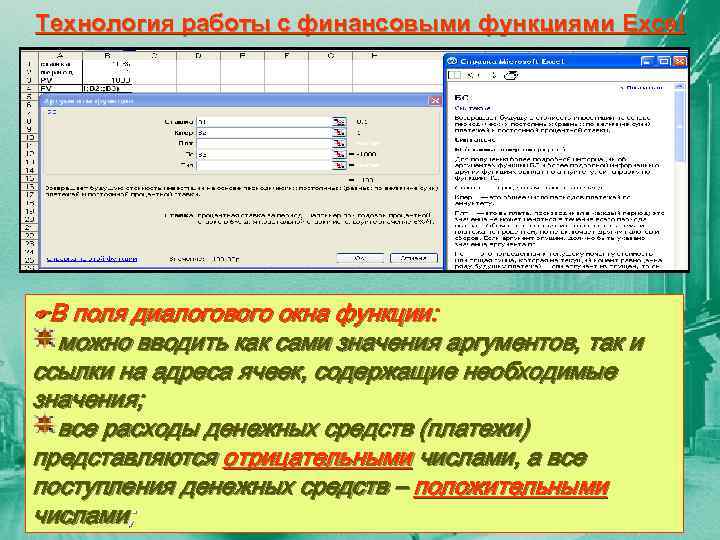Технология работы с финансовыми функциями Excel В поля диалогового окна функции: можно вводить как сами значения аргументов, так и ссылки на адреса ячеек, содержащие необходимые значения; все расходы денежных средств (платежи) представляются отрицательными числами, а все поступления денежных средств – положительными числами;

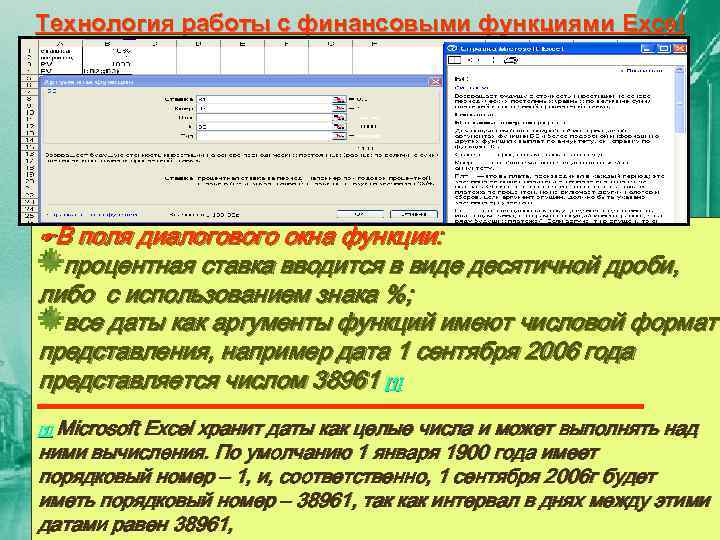Технология работы с финансовыми функциями Excel В поля диалогового окна функции: процентная ставка вводится в виде десятичной дроби, либо с использованием знака %; все даты как аргументы функций имеют числовой формат представления, например дата 1 сентября 2006 года представляется числом 38961 [1] Microsoft Excel хранит даты как целые числа и может выполнять над ними вычисления. По умолчанию 1 января 1900 года имеет порядковый номер – 1, и, соответственно, 1 сентября 2006 г будет иметь порядковый номер – 38961, так как интервал в днях между этими датами равен 38961, [1]

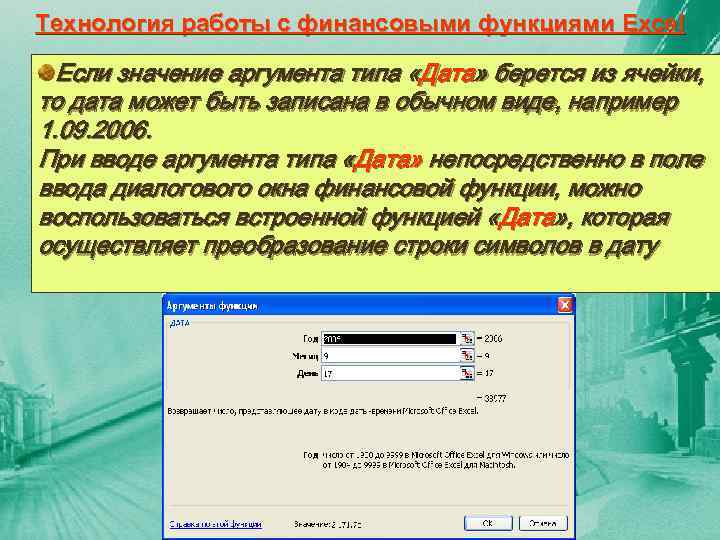Технология работы с финансовыми функциями Excel Если значение аргумента типа «Дата» берется из ячейки, то дата может быть записана в обычном виде, например 1. 09. 2006. При вводе аргумента типа «Дата» непосредственно в поле ввода диалогового окна финансовой функции, можно воспользоваться встроенной функцией «Дата» , которая осуществляет преобразование строки символов в дату

Технология работы с финансовыми функциями Excel Для вычисления характеристик финансовых операций с наращением и дисконтированием вложенных сумм удобно использовать функции БС(), ПС(), КПЕР(), НОРМА(), БЗРАСПИС(), НОМИНАЛ(), ЭФФЕКТ(). Большинство финансовых функций имеет одинаковый набор базовых аргументов: ставка - процентная ставка за период (норма доходности или цена заемных средств – r ). Например, если получена ссуда на автомобиль под 10 процентов годовых и делаются ежемесячные выплаты, то процентная ставка за месяц составит 10%/12 или 0, 83%. В качестве значения аргумента ставка нужно ввести в формулу 10%/12 или 0, 83% или 0, 0083

Технология работы с финансовыми функциями Excel кпер - срок (число периодов n) проведения операции. Например, если получена ссуда на 4 года под приобретение автомобиля и делаются ежемесячные платежи, то ссуда имеет 4*12 (или 48) периодов. В качестве значения аргумента кпер в формулу нужно ввести число 48. Плт - выплата, производимая в каждый период и не меняющаяся за все время выплаты ренты. Обычно выплаты включают основные платежи и платежи по процентам, но не включают других сборов или налогов. Например, ежемесячная выплата по четырехгодичному займу в 10 000 руб. под 12 процентов годовых составит 263, 33 руб. В качестве значения аргумента выплата нужно ввести в формулу число 263, 33.

Технология работы с финансовыми функциями Excel Пс - это приведенная к текущему моменту стоимость (величина PV) или общая сумма, которая на текущий момент равноценна ряду будущих платежей. Если аргумент ПС опущен, то он полагается равным 0. В этом случае должно быть указано значение аргумента Плт. ; Бс - требуемое значение будущей стоимости (FV) или остатка средств последней выплаты. Если аргумент опущен, он полагается равным 0 (будущая стоимость займа, например, равна 0). Например, если предполагается накопить 50000 руб. для оплаты специального проекта в течение 18 лет, то 50 000 руб. это и есть будущая стоимость

Технология работы с финансовыми функциями Excel [тип] - число 0 или 1, обозначающее, когда должна производиться выплата: 1 - начало периода (обычная рента или пренумерандо), 0 - конец периода (постнумерандо)], необязательный аргумент При необходимости корректировки значений аргументов функции (изменении адресов ссылок, постоянных значений и др. ): установить курсор в ячейку, содержащую формулу: Выполнить редактирование аргументов функции в строке формул либо повторно вызвать, используя «Мастер функций» , диалоговое окно функции и в нем выполнить необходимую коррекцию

Денежные потоки Проведение практически любой финансовой операции порождает движение денежных средств. Такое движение может характеризоваться возникновением отдельных платежей, или множеством выплат и поступлений, распределенных во времени. В финансовой практике широко распространены контракты, предусматривающие не разовое, а систематическое движение средств – выплаты/поступления по заданному графику происходят регулярно

Денежные потоки В процессе количественного анализа финансовых операций, удобно абстрагироваться от их конкретного экономического содержания и рассматривать порождаемые ими движения денежных средств как численный ряд, состоящий из последовательности распределенных во времени платежей CF 0, CF 1, . . . , Cfn. Для обозначения подобного ряда в мировой практике широко используется термин “поток платежей” или “денежный поток [2]” (cash flow – CF). [1] Заметим, что платежи могут быть неодинаковы не только по знаку и величине самого платежа, но и по времени их поступления. Ø [2] Рассмотренные ранее наращение и дисконтирование вложенной суммы может также рассматриваться как денежный поток с однократным поступлением денег и единичным периодом накопления.

Денежные потоки Каждый отдельный элемент такого численного ряда CFt представляет собой разность между всеми поступлениями (притоками) денежных средств и их расходованием (оттоками) на конкретном временном отрезке проведения финансовой операции. Таким образом, величина CFt может иметь как положительный, так и отрицательный знак.

Денежные потоки Количественный анализ денежных потоков, генерируемых за определенный период времени в результате реализации финансовой операции, или функционирования каких-либо активов, в общем случае сводится к исчислению следующих характеристик: FVn – будущей стоимости потока за n периодов; PVn – современной стоимости потока за n периодов. Часто возникает необходимость определения и ряда других параметров финансовых операций, важнейшими из которых являются: CFt – величина потока платежей в периоде t; r – процентная ставка; n – срок (количество периодов) проведения операции

Денежные потоки в виде серии равных платежей (аннуитеты) Поток платежей, все члены которого имеют одинаковое направление (знак), а временные интервалы между последовательными платежами постоянны, называется финансовой рентой или аннуитетом [1] (англ. annuity). __________________________ [1] Это частный случай потока платежей, все члены которого - положительные величины. Примерами аннуитета могут быть регулярные взносы в пенсионный или другие фонды, выплаты процентов по ценным бумагам, например, по акциям и т. д.

Денежные потоки в виде серии равных платежей (аннуитеты) При рассмотрении финансовой ренты используются следующие основные категории: член ренты (Cft) – величина каждого отдельного платежа; период ренты (t) – временной интервал между членами ренты; срок ренты (n) – время от начала финансовой ренты до конца последнего ее периода; процентная ставка (r) – ставка, используемая при наращении платежей, из которых состоит рента.

Денежные потоки : Классификация финансовых рент: В зависимости от периода продолжительности ренты годовая рента ежегодные платежи, (т. е. период ренты равен 1 году); ----------------------------Срочная рента, период ренты может иметь любую продолжительность (как более, так и менее года). По числу начислений процентов ренты с начислением 1 раз в год; m раз в год; непрерывное начисление.

Денежные потоки Классификация финансовых рент: По величине членов ренты могут быть постоянные величина каждого отдельного платежа постоянна, (т. е. рента с равными ренты членами); ---------------------------величина платежа варьирует, т. е. рента переменные с неравными членами. ренты По числу членов ренты различают с конечным числом с бесконечным числом (ограниченные ренты), когда число членов ренты конечно и заранее известно ; (вечные ренты), когда число ее членов заранее не известно.

Денежные потоки Классификация финансовых рент: По вероятности выплаты ренты подлежат безусловной выплате, т. е. не верные ренты зависят не от каких условий, например, погашение кредита; ---------------------------условные ренты зависят от наступления некоторого случайного события По методу выплаты платежей на практике встречаются чаще всего, обычные ренты – с выплатой платежа в конце периода ренты (постнумерандо); с выплатой в начале периода ренты (пренумерандо).

Денежные потоки в виде серии равных платежей (аннуитеты) Тип аннуитета задает распределение n платежей одинакового размера по границам процентных периодов внутри срока аннуитета

Денежные потоки в виде серии равных платежей (аннуитеты) В финансовой практике наиболее часто встречаются так называемые простые или обыкновенные аннуитеты (ordinary annuity, regular annuity), которые предполагают получение или выплаты одинаковых по величине сумм на протяжении всего срока операции в конце / начале каждого периода (года, полугодия, квартала, месяца) (1) Выплаты по облигациям с фиксированной ставкой купона, банковским кредитам, долгосрочной аренде, страховым полисам, формирование различных фондов – все это далеко неполный перечень финансовых операций, денежные потоки которых, представляют собой обыкновенные аннуитеты

Определение характеристик простых денежных потоков В отличие от разовых платежей, рассмотренных нами ранее, для количественного анализа аннуитетов нам понадобятся все выделенные ранее характеристики денежных потоков: FV, PV, CF, r и n. ( и соответственно, все аргументы рассмотренных ранее финансовых функций Excel.

Определение характеристик простых денежных потоков При проведении расчетов в ПП Excel используются основные функции: БС() – оценка наращенной суммы ПС() - оценка приведенной стоимости КПЕР() - количество периодов начисления СТАВКА() - процентная ставка; ПЛТ() - сумма периодического , регулярного платежа;

Определение характеристик простых денежных потоков Будущая величина потока платежей FV Наращенная сумма – сумма всех платежей с начисленными на них процентами к концу срока ренты. (Это может быть обобщенная сумма задолженности, итоговый объем инвестиций и т. п. ) r r CF CF r FV CF n t(время)

Определение характеристик простых денежных потоков Пример На счет в банке в течении пяти лет в конце каждого года будут вноситься суммы в размере 500 руб. , на которые будут начисляться проценты по ставке 30%. Определить сумму, которую банк выплатит владельцу счета. FVn=CF*(1+r)n-1+ CF*(1+r)n-2+…+ CF FV 5 = = 4521, 55 =4521, 55

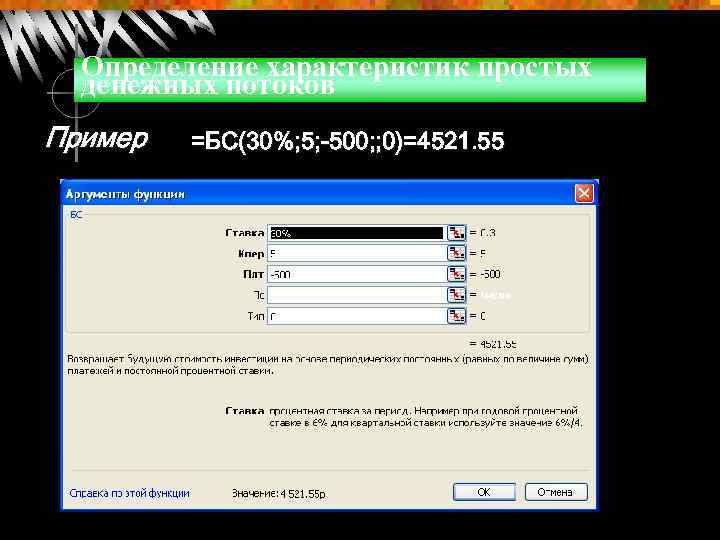Определение характеристик простых денежных потоков Пример =БС(30%; 5; -500; ; 0)=4521. 55

Определение характеристик простых денежных потоков Платежи могут осуществляться j-раз в году (ежемесячно, ежеквартально и т. д. ). В этом случае общее число платежей за n-лет будет равно m*n, процентная ставка – r / m, а величина платежа – CF / m.

Определение характеристик простых денежных потоков Пример Предположим, что каждый год ежемесячно в банк помещается сумма в 1000. Ставка равна 12% годовых, начисляемых в конце каждого месяца. Какова будет величина вклада к концу 4 -го года ? Общее количество платежей за 4 года равно: 4* 12 = 48. Ежемесячная процентная ставка составит: 12 / 12 = 1%.

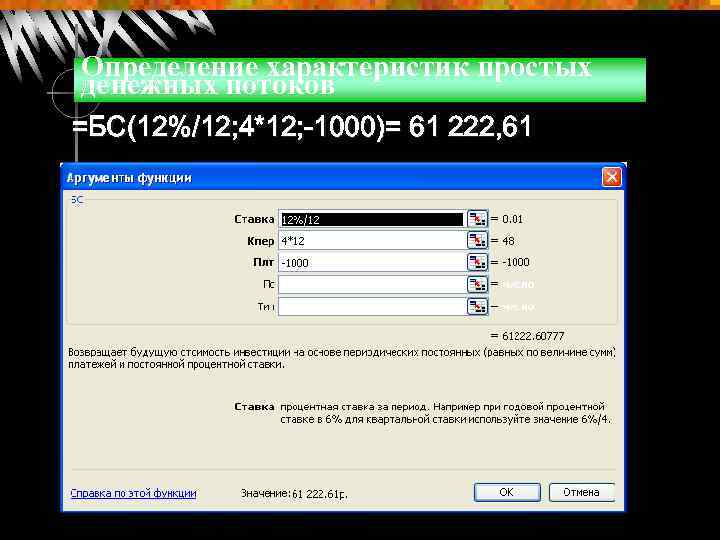Определение характеристик простых денежных потоков =БС(12%/12; 4*12; -1000)= 61 222, 61

Современная (текущая) величина аннуитета (PV) Современная (текущая) величина потока платежей (капитализированная или приведенная величина) – это сумма платежей, дисконтированных на момент начала ренты по ставке начисляемых сложных процентов. Это важнейшая характеристика финансового анализа, т. к. является основой для измерения эффективности различных финансовокредитных операций, сравнения условий контрактов и т. п. Данная характеристика показывает, какую сумму следовало бы иметь первоначально, чтобы, разбив ее на равные взносы, на которые начислялись бы установленные проценты, можно было бы получить необходимую наращенную сумму

Современная (текущая) величина аннуитета (PV) Общее соотношение для определения текущей величины PV аннуитета при сложной процентной ставке r и длительности потока платежей n лет имеет вид Пример: Пусть мы хотим получать доход, равный $1000 в год, на протяжении 4 -х лет. Какая сумма обеспечит такой доход, если ставка по срочным депозитам равна 10% годовых? Решение. PV = 1000*[((1 -(1+10%)-4)/10%= 3169, 87. В Excel используется финансовая функция ПС( ): =ПС(10%; 4; -1000)=3169. 87