Финансовая математика Модели однократных инвестиций капитала Основные

Финансовая математика Модели однократных инвестиций капитала

Основные понятия Финансовая математика изучает соотношения между размерами платежей, сроками выплат и процентными ставками, возникающими в коммерческих сделках и финансовобанковских операциях.

Формулы для моделей финансовой математики. Схема простых процентов Простейший вид финансовой сделки – однократное предоставление в долг в некоторый начальный момент t = 0 суммы S(0) под r % с условием, что в момент t = T будет возвращена сумма S(T). Начальный момент t = 0 Конечный момент t = T Начальная сумма S(0) Наращенная сумма S(T) Годовая %-я ставка r 1. Формула расчета наращенной суммы по схеме простых процентов: . S(T) = S(0) (1 + r T). Обычно она применяется при сроке сделке, меньшем 1 года. Однако при таких расчетах срок сделки всегда приводится к базовому периоду в год.

• Эффективность такой операции определяется показателями r и d

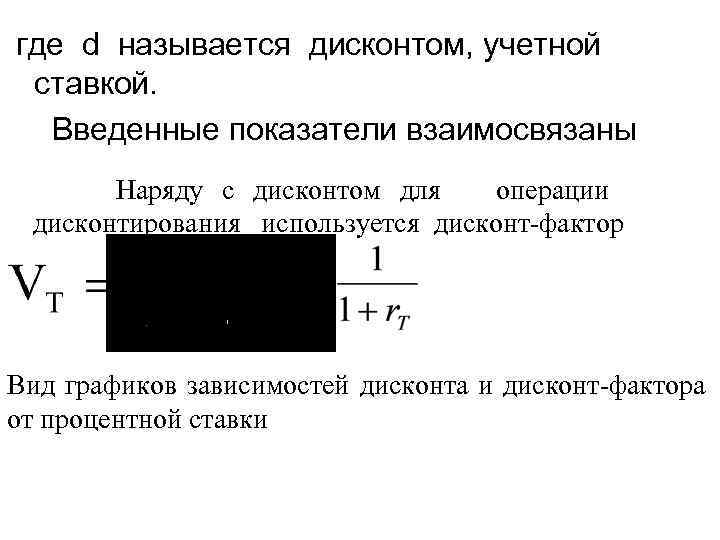где d называется дисконтом, учетной ставкой. Введенные показатели взаимосвязаны Наряду с дисконтом для операции дисконтирования используется дисконт-фактор Вид графиков зависимостей дисконта и дисконт-фактора от процентной ставки

В условиях финансовых операций как правило оговариваются процентная и учетная ставки за базовый период, равный году. Соответствующие показатели за фактический период T Будем называть процентную и учетную ставки за годовыми и обозначать их через r и d

Пример: S(0) = 18 000 руб. r = 33 % ( = 0, 33) T = 4 мес. ( =4/12) S(T) – ? S(T) = S(0) (1 + r T) => S(T) = 18 000 ( 1 + 0, 33 4/12 ) = 19 890 руб. Иногда в практике финансовых расчетов возникает необходимость решения обратной задачи – расчета начальной суммы S(0) по известной наращенной сумме S(T), процентной ставе r и сроку T. Процесс приведения наращенной суммы в момент t = T к моменту t = 0 называется дисконтированием. Для схемы простых процентов формула дисконтирования: выводится следующим образом: .

Иногда для удобства отдельно рассчитывается частное , которое называется дисконт-фактором. Тогда S(0) = V S(T).

Помимо расчета начальной и наращенной сумм в моделях однократных инвестиций возможен расчет и других параметров коммерческой сделки. Так, для схемы простых % из формулы S(T) = S(0) (1 + r T) выводятся формулы для расчета годовой процентной ставки r и срока финансовой операции T:

Схема сложных процентов (капитализация %) Для операций, срок которых составляет более 1 года, обычно используют схему сложных процентов, при которой производится капитализация %, т. е. % начисляются не на первоначальную сумму S(0), а на наращенную к моменту капитализации. 1. Формула расчета наращенной суммы по схеме сложных процентов: . В пакете М. Excel предусмотрена функция для расчета наращенной суммы S(T) по схеме сложных %: БС ( r ; T ; ; S(0) )

Во многих случаях в практике финансовых расчетов приходится по известным значениям наращенной суммы S(T), капитала S(0) определять период T или годовую процентную ставку r. Для схемы простых процентов соответствующие соотношения имеют вид

• Для расчета параметров рассматриваемых финансовых операций удобно использовать табличные процессоры для персональных компьютеров. Табличный процессор Excel содержит специальные табличные функции для расчета параметров S(T), T и r по схеме сложных процентов. Приведем корректную запись этих функций. Для Excel 2000 и ранних версий эти функции имеют вид S(T)=Бс(r; T; ; S(0)) , T= КПЕР(r; ; S(0); S(T)) , r = СТАВКА(T; ; S(0); S(T)) и могут быть введены с помощью специального инструмента Excel Мастера функций. Конечно же для вычисления этих параметров можно запрограммировать клетки электронной таблицы путем использования элементарных арифметических операций по соответствующим формулам (тем более это верно для всех соотношений схемы простых процентов). Однако для схемы сложных процентов рациональнее использовать приведенные табличные функции.

Эффективная ставка процента В практике финансовых расчетов используются схемы, при которых проценты на капитал начисляются несколько раз в году. При этом оговариваются годовая процентная ставка r и количество начислений в течение года m. Фактически в этом случае за базовый период принимается 1/m часть года со ставкой сложных процентов r/m. В результате

Пример. Облигация номиналом 100 т. руб. выпущена на 5 лет при номинальной (годовой) ставке процента 10 %. Держатель облигации будет капитализировать проценты. Определить наращенную стоимость при начислении процентов 1 раз в год (m = 1), раз в полугодие (m = 2), раз в квартал (m = 4). (Облигация - долговое обязательство эмитента, выпустившего ценную бумагу, уплатить владельцу облигации в оговоренный срок номинальную стоимость бумаги и через оговоренные периоды - фиксированный или плавающий процент. ) Приведем расчеты для примера. m = 1 , S(5) = , m = 2 , S(5) = , m = 4 , S(5) =. При количестве начислений m в течение года годовая ставка процента r называется номинальной. Чем больше количество начислений m , тем больше наращенная стоимость S(T).

Т(r; m) , Электронные таблицы Excel позволяют рассчитать эффективную процентную ставку по номинальной и решить обратную задачу с помощью табличных функций. Их формат имеет вид r-= ЭФФЕКТ(r; m) ,

Модели потоков платежей Последовательность распределенных во времени выплат и платежей называется потоком платежей. Финансовые ренты Поток платежей, все составляющие которого имеют одну и ту же величину и поступают через одинаковые интервалы времени, называется финансовой рентой, или аннуитетом. Финансовая рента называется постоянной, если все платежи имеют одинаковую величину. Для финансовой ренты характерно, что платежи С в любой момент времени t равны между собой: C(t) C = const. Наращенная сумма всех периодических платежей потока равна

В пакете М. Excel предусмотрена функция для расчета наращенной суммы финансовой ренты S(n) по схеме сложных %: БС( r ; n ; C ) Дисконтирование финансовой ренты:

величина процентной ставки r = СТАВКА( n ; C ; ; S(n) ) При расчете периодического платежа C часть этого платежа в каждый момент выплаты t ( идет на погашение основного долга (кредита) Сосн, а часть – на погашение процентов по кредиту Спроц. С = Сосн. + Спроц. Для определения сумм погашения основного долга и процентов по нему в Excel существуют функции:

Сосн = ОСПЛТ ( r ; t ; n ; -S(0) ) – рассчитывается для всех t от 1 до n; Спроц = ПРПЛТ ( r ; t ; n ; -S(0) ) – рассчитывается для всех t от 1 до n. ПЛТ = ОСПЛТ + ПРПЛТ

Наращенные суммы постоянных финансовых рент. Рассмотрим наращенную сумму финансовой ренты в момент t = n. При этом следует иметь ввиду, что наращение суммы финансовой ренты осуществляется не только за счет начисления процентов, как это имеет место для разовых платежей, но и за счет добавления периодических платежей. Чтобы определить величину наращенной суммы, будем рассуждать следующим образом. Платеж С(!) будет наращиваться (n-1) лет и возрастет до величины. Платеж С(2) будет наращиваться в течение (n-2) лет и увеличится до значения

Нерегулярные потоки платежей. В общем случае отдельные платежи потока имеют разную величину и поступают в любые (непериодические) моменты времени. Поток платежей с такими свойствами называется нерегулярным потоком. Рассмотрим нерегулярный поток, предусматривающий платежи C(t) в моменты времени t = t 1, t 2, . . . , tn. Наращенная сумма такого потока платежей, приведенная к моменту t = T >=tn , определяется выражением

Двусторонние потоки платежей

Учёт комиссии для ссуд и кредитов