Финансовая Математика ч 1 краткий обзор 1

Финансовая Математика ч. 1 (краткий обзор) 1

Временная стоимость денег u u Простые проценты u Сложные проценты u 2 Процентная ставка Погашение долга

Процентная ставка Что предпочесть - $10 000 сегодня или $10, 000 через 5 лет? лет Очевидно $10 000 сегодня Этот факт есть проявление Временной стоимости денег!! денег 3

Почему ВРЕМЯ? Почему время так важно при прнятии финансовых рещений? Время дает возможность отложить потребление сейчас и взамен увеличить потребление в будущем за счет получения процентов 4

Типы процентов u Простые проценты Проценты начисляются только на инвестированный капитал или основной долг u Сложные проценты Проценты начисляются как на основной капитал так и на проценты начисленные ранее (за прошлые периоды) 5

Формула простых процентов Формула I = P 0 i n I: P 0: Основной капитал (t=0) i: Процентная ставка (за период) n: 6 Простые проценты Число периодов

Простые проценты -пример u Предположим что вы внесли на 2 года $1 000 на счет по которому начисляются 7% годовых. Какова сумма начисленных процентов в конце 2 -го года? u 7 I = P 0 i n = $1, 000(0. 07)(2) = $140

Простые проценты - Будущая (накопленная) стоимость (FV) u Какова будущая стоимость (FV) вклада? FV FV = P 0 + I = $1, 000 + $140 = $1140 Будущая стоимость - стоимость в некоторый момент времени в будущем сегодняшней (текущей) суммы (платежа) или серии таких сумм (платежей), для заданной процентной ставки (выражающей стоимость денег). 8

Текущая стоимость (PV) u Какова текущая стоимость (PV) в предыдущей задаче? PV Текущая (сегодняшняя, приведенная) стоимость вклада есть $1 000 начальной суммы вклада. Такова его стоимость сегодня! u 9 Текущая стоимость - стоимость в текущий (сегодняшний) момент времени будущих сумм (платежей) или серии таких сумм (платежей) при заданной процентной ставке rate.

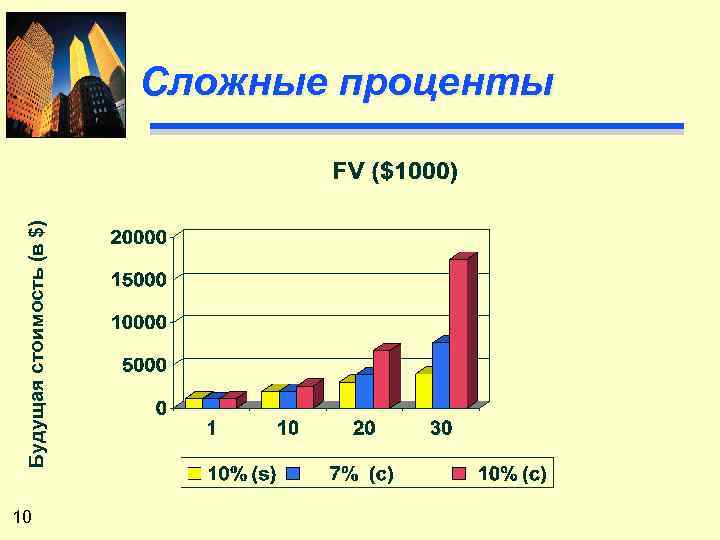
Будущая стоимость (в $) Сложные проценты 10

Будушая стоимость (временная диаграмма) Пусть $1 000 вложено под 7% годовых (сложные проценты) на 2 года 0 7% 1 2 $1000 FV 2 11

Будущая стоимость суммы (Формула) FV 1 = P 0 (1+i)1 = $1000 (1. 07) = $1070 Сложные проценты За первый год проценты по вкладу $1000 составят $70. Простые проценты по вкладу за год составят точно такую же сумму. 12

Будущая стоимость суммы (Формула) FV 1 = P 0 (1+i)1 = $1000 (1. 07) = $1070 FV 2 = FV 1 (1+i)1 = P 0 (1+i) = $1000(1. 07) $1000 = P 0 (1+i)2 = $1000(1. 07)2 $1000 = $1144. 90 13 За второй год по сложным процентам будет начислено на $4. 90 больше чем по простым.

Формула сложных процентов FV 1 = P 0(1+i)1 FV 2 = P 0(1+i)2 ит. д. Формула будущей стоимости: стоимости FVn = P 0 (1+i)n или FVn = P 0 (аi, n) -- см. Табл. I 14

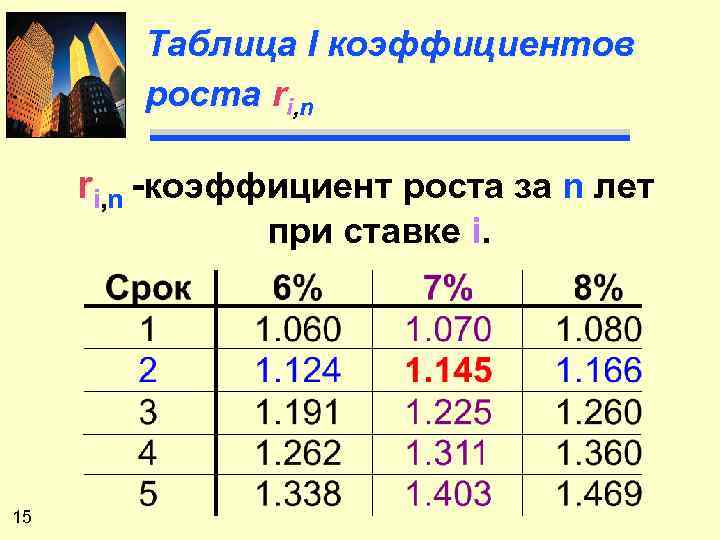
Таблица I коэффициентов роста ri, n -коэффициент роста за n лет при ставке i. 15

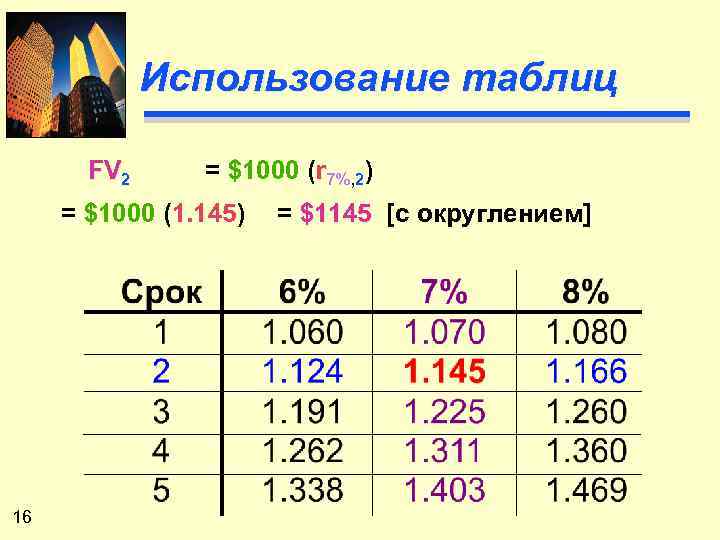
Использование таблиц FV 2 = $1000 (r 7%, 2) = $1000 (1. 145) 16 = $1145 [с округлением]

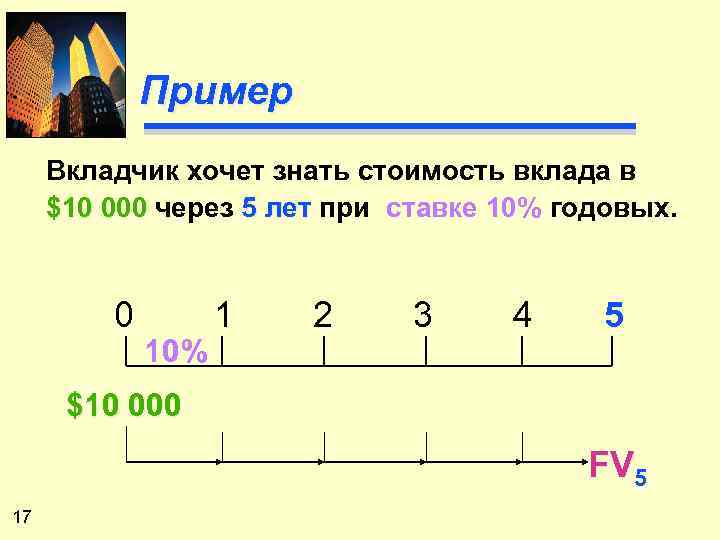
Пример Вкладчик хочет знать стоимость вклада в $10 000 через 5 лет при ставке 10% годовых. 0 10% 1 2 3 4 5 $10 000 FV 5 17

Решение u Вычисление по формуле: FVn = P 0 (1+i)n FV 5 = $10 000 (1+ 0. 10)5 = $16105. 10 u Вычисление по таблице I: FV 5 = $10000 (r 10%, 5) = $10000 (1. 611) = $16110 [с округлением] 18

Удвоение суммы вклада!!! За какой срок удвоится вклад в $5, 000 по сложной ставке 12% годовых? Используем “правило 72 -х”. 19

“Правило 72 -х” За какой срок удвоится вклад в $5000 по сложной ставке 12% годовых? Приблизительное число лет необходимое для удвоения вклада = 72 / i% = 72 / 12% = 6 лет [точное время удвоения- 6. 12 года] 20

Текущая стоимость суммы Пусть вкладчик хочет накопить $1000 за 2 года. Какую сумму он должен вложить сегодня по ставке 7% годовых начисляемых ежегодно. 0 7% 1 2 $1000 PV 0 21 PV 1

Текущая стоимость суммы (Формула) PV 0 = FV 2 / (1+i)2 0 7% = $1000 / (1. 07)2 = $873. 44 1 2 $1000 PV 0 22

Формула текущей стоимости PV 0 = FV 1 / (1+i)1 PV 0 = FV 2 / (1+i)2 ит. д . . . Формула текущей стоимости: стоимости PV 0 = FVn / (1+i)n или PV 0 = FVn vi, n -- см. табл. II 23

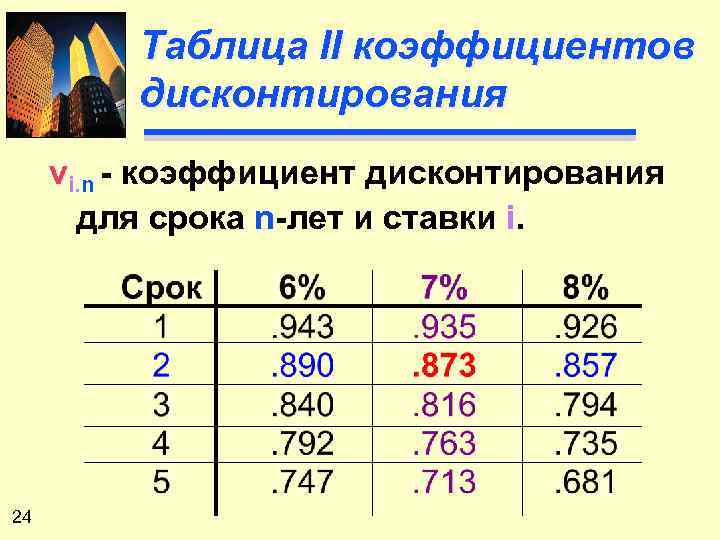
Таблица II коэффициентов дисконтирования vi. n - коэффициент дисконтирования для срока n-лет и ставки i. 24

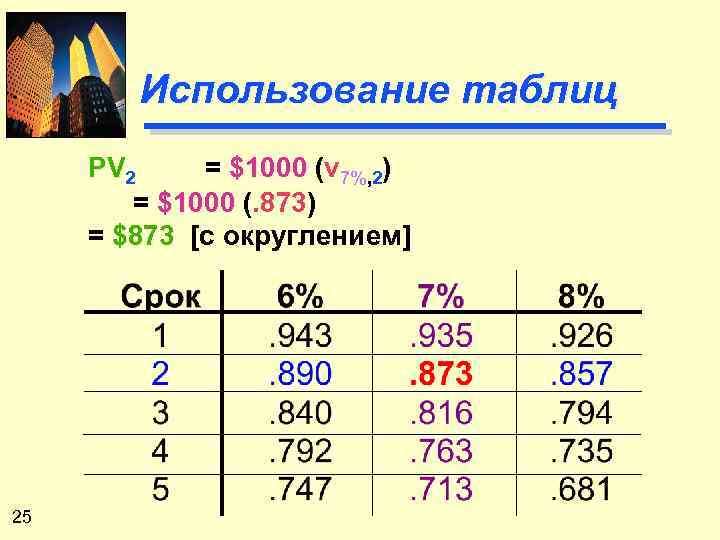
Использование таблиц PV 2 = $1000 (v 7%, 2) = $1000 (. 873) = $873 [с округлением] 25

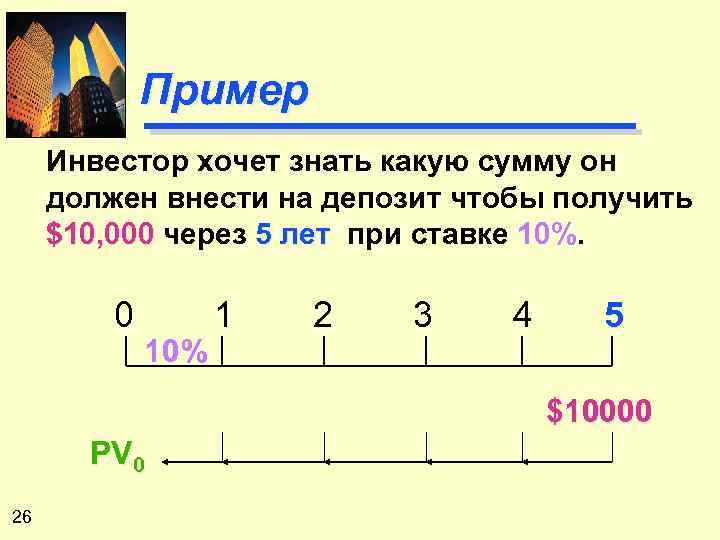
Пример Инвестор хочет знать какую сумму он должен внести на депозит чтобы получить $10, 000 через 5 лет при ставке 10%. 0 10% 1 2 3 4 5 $10000 PV 0 26

Решение u Вычисление по формуле: PV 0 = FVn / (1+i)n PV 0 = $10000 / (1+ 0. 10)5 = $6209. 21 u 27 Вычисление по таблице II: PV 0 = $10, 000 (V 10%, 5) = $10000 (. 621) = $6210. 00 [с округлением]

Ренты (аннуитеты) u u Обыкновенная рента: Платежи рента осуществлячются в конце каждого периода. u 28 Рента - регулярный поток платежей т. е. последовательность одинаковых платежей через одинаковые периоды времени Авансированная рента: Платежи рента осуществлячются в начале каждого периода.

Примеры рент u Погашение займов u u Страховые взносы u Платежи по закладной u 29 Купонные платежи по облигации Взносы в пенсионный фонд

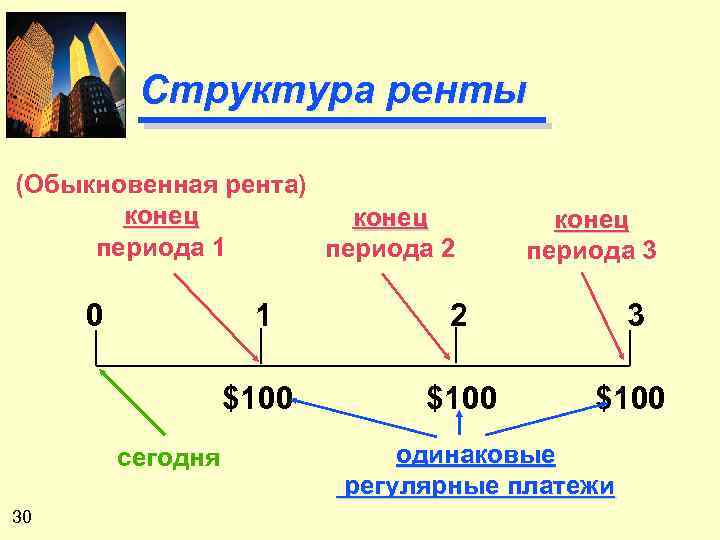
Структура ренты (Обыкновенная рента) конец периода 1 периода 2 0 конец периода 3 1 30 3 $100 сегодня 2 $100 одинаковые регулярные платежи

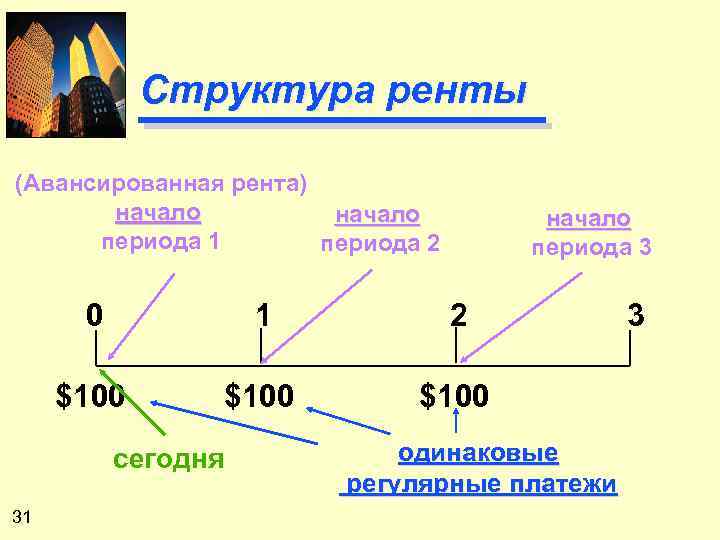
Структура ренты (Авансированная рента) начало периода 1 периода 2 начало периода 3 0 1 2 $100 сегодня 31 одинаковые регулярные платежи 3

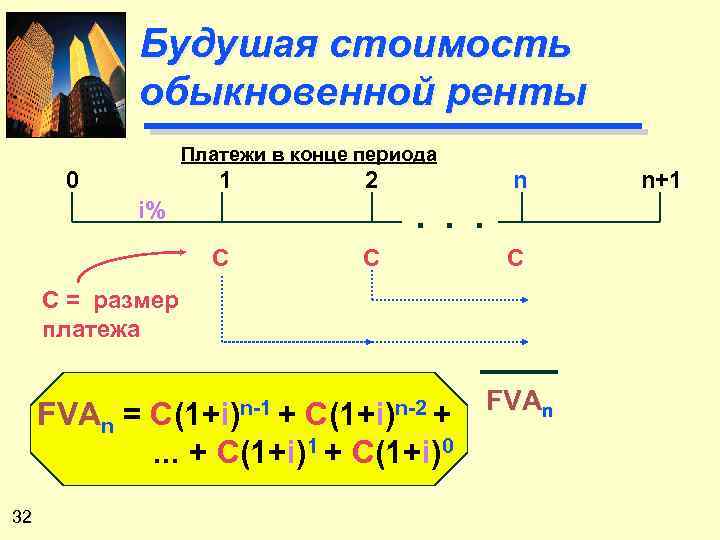
Будушая стоимость обыкновенной ренты Платежи в конце периода 0 1 2 n . . . i% С С(1+i)n-1 + С(1+i)n-2 + FVAn С = размер платежа FVAn = 32 . . . + С(1+i)1 + С(1+i)0 n+1

Пример Платежи в конце периода 0 1 2 3 $1, 000 4 $1, 000 7% $1, 000 $1, 070 $1, 145 FVA 3 = $1, 000(1. 07)2 + $1, 000(1. 07)1 + $1, 000(1. 07)0 $3, 215 = FVA 3 = $1, 145 + $1, 070 + $1, 000 = $3, 215 33

Замечание о будущей стоимости рент 34 Будущая стоимость обыкновенной ренты вычисляемая относительно конца последнего периода ренты, совпадает с будущей стоимостью авансированной ренты рассматриваемой относительно начала последнего периода.

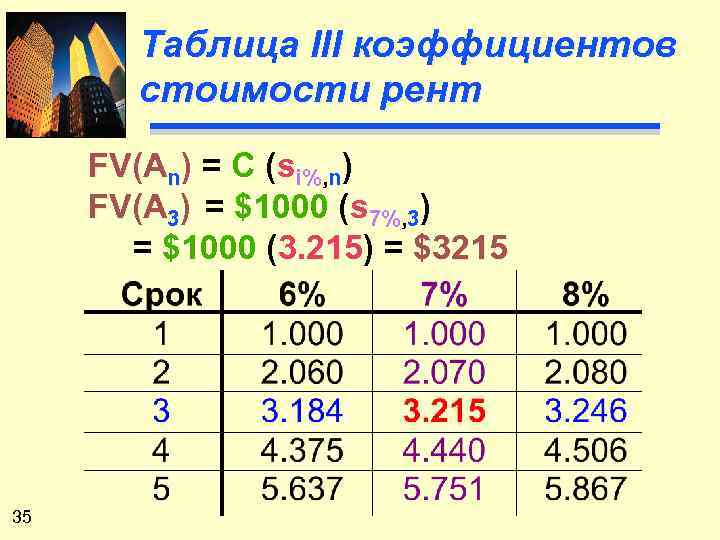
Таблица III коэффициентов стоимости рент FV(An) = C (si%, n) FV(A 3) = $1000 (s 7%, 3) = $1000 (3. 215) = $3215 35

Будущая стоимость авансированной ренты Платежи в начале периода 0 1 2 3 C C C i% C . . . FV(Ăn) = C(1+i)n + C(1+i)n-1 +. . . + C(1+i)2 + C(1+i)1 = FV(An )(1+i) 36 n-1 n C FV(Ăn)

Пример Платежи в начале периода 0 1 2 3 $1, 000 4 $1, 070 7% $1, 000 $1, 145 $1, 225 FV(Ă3)= $1, 000(1. 07)3 + $3, 440 = FV(Ă3) $1, 000(1. 07)2 + $1, 000(1. 07)1 = $1, 225 + $1, 145 + $1, 070 = $3, 440 37

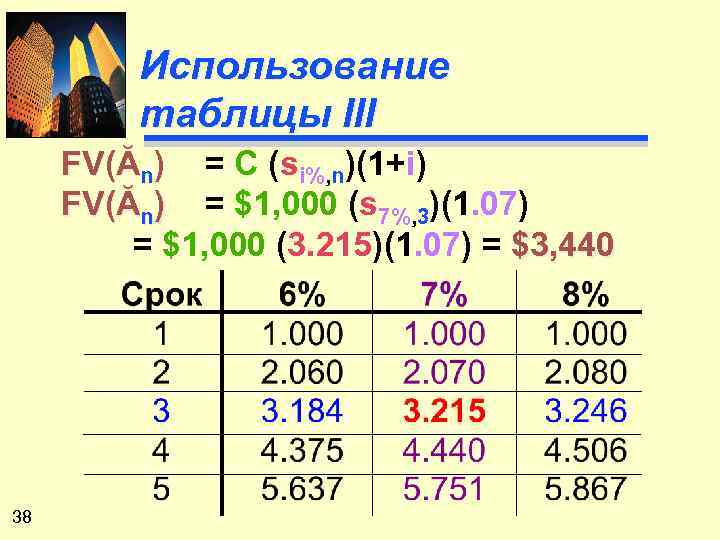
Использование таблицы III FV(Ăn) = C (si%, n)(1+i) FV(Ăn) = $1, 000 (s 7%, 3)(1. 07) = $1, 000 (3. 215)(1. 07) = $3, 440 38

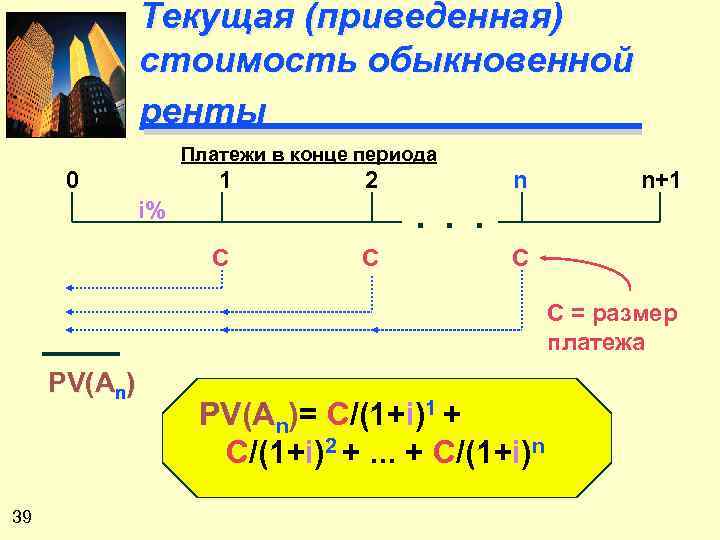
Текущая (приведенная) стоимость обыкновенной ренты Платежи в конце периода 0 1 2 n n+1 . . . i% C C = размер платежа PV(An) 39 PV(An)= C/(1+i)1 + C/(1+i)2 +. . . + C/(1+i)n

Пример Платежи в конце периода 0 1 2 3 $1, 000 4 $1, 000 7% $ 934. 58 $ 873. 44 $ 816. 30 $1, 000 $2, 624. 32 = PVA 3 40 PV(A 3)= $1, 000/(1. 07)1 + $1, 000/(1. 07)2 + $1, 000/(1. 07)3 = $934. 58 + $873. 44 + $816. 30 = $2, 624. 32

Замечание о текущей стоимости рент Текущая стоимость обыкновенной ренты вычисляемая относительно конца первого периода ренты, совпадает с текущей стоимостью авансированной ренты рассматриваемой относительно начала первого периода. 41

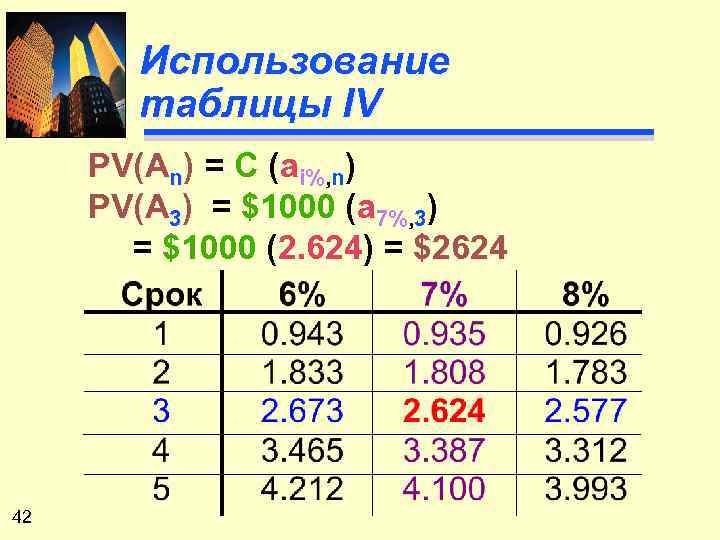
Использование таблицы IV PV(An) = C (ai%, n) PV(A 3) = $1000 (a 7%, 3) = $1000 (2. 624) = $2624 42

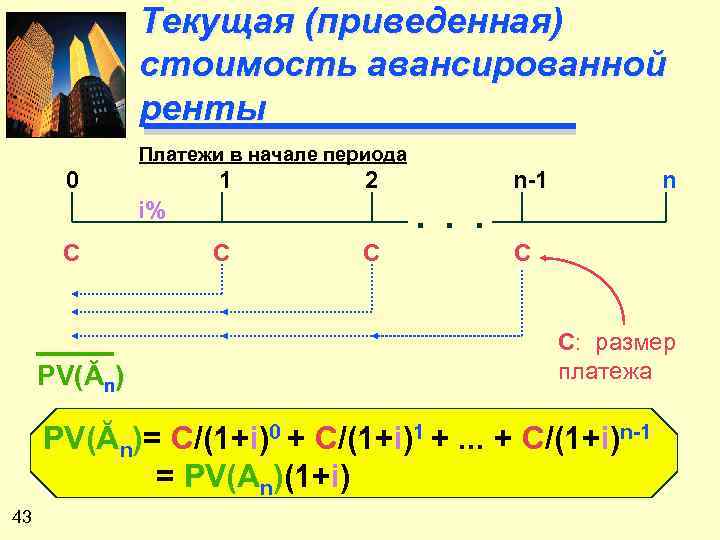
Текущая (приведенная) стоимость авансированной ренты Платежи в начале периода 0 1 2 PV(Ăn) n . . . i% C n-1 C C: размер платежа PV(Ăn)= C/(1+i)0 + C/(1+i)1 +. . . + C/(1+i)n-1 = PV(An)(1+i) 43

Пример Платежи в начале периода 0 1 2 $1000 3 $1000 7% $ 1000. 00 $ 934. 58 $ 873. 44 $2, 808. 02 = PV(Ă3)= $1000/(1. 07)0 + $1000/(1. 07)1 + $1000/(1. 07)2 = $2808. 02 44 4

Использование таблицы IV PV(Ăn)= C (аi%, n)(1+i) PV(A 3)= $1, 000 (а 7%, 3)(1. 07) = $1, 000 (2. 624)(1. 07) = $2, 808 45

Этапы решения задач финансовой математики 1. Анализ задачи 2. Определение временных параметров 3. Определение финансовых параметров 4. Построение потоков платежей задачи 5. Выбор момента приведения (полюса) 6. Приведение потоков платежей к полюсу 7. Составление уравнения баланса 8. Решение уравнения баланса и нахождение требуемых параметров 46

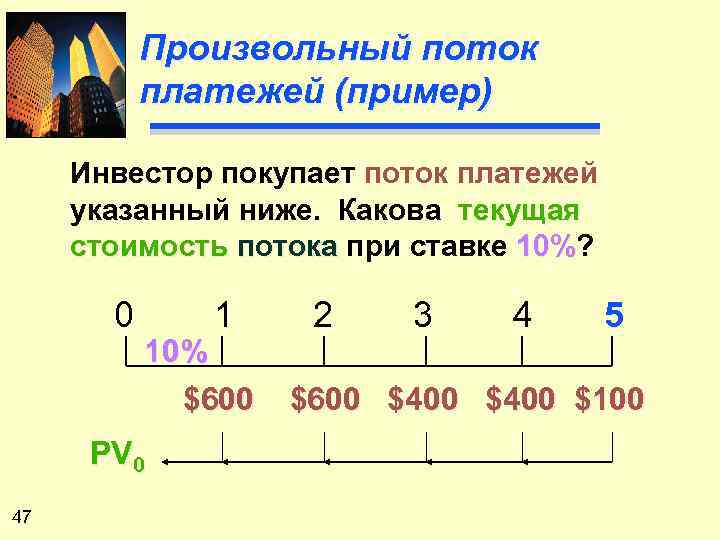
Произвольный поток платежей (пример) Инвестор покупает поток платежей указанный ниже. Какова текущая стоимость потока при ставке 10%? 10% 0 10% $600 PV 0 47 1 2 3 4 5 $600 $400 $100

Два способа решения 1. Дисконтируем поток платежей дисконтируя отдельные платежи к моменту (полюсу) t=0. 2. Разлагаем поток на суммучастей, состоящих из рент и отдельных платежей. Затем дисконтируем эти части к моменту t=0. 48

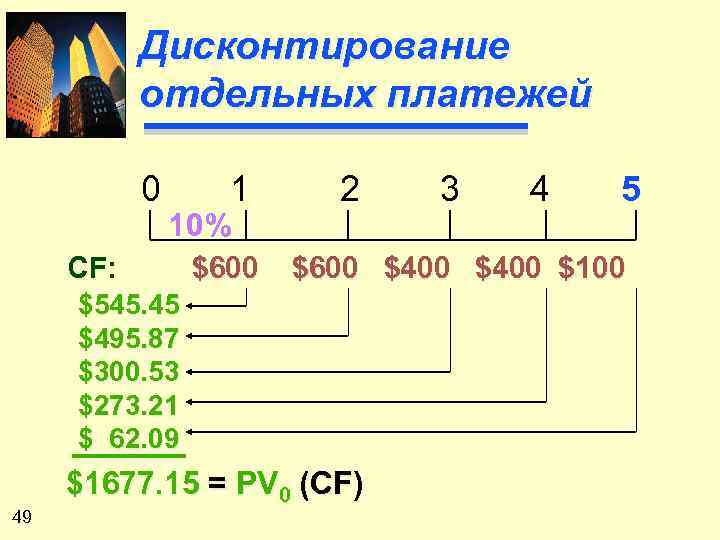
Дисконтирование отдельных платежей 0 1 10% CF: $600 2 4 5 $600 $400 $100 $545. 45 $495. 87 $300. 53 $273. 21 $ 62. 09 49 3 $1677. 15 = PV 0 (CF)

Разложение потока платежей на части (#1) 0 10% CF: 1 $600 2 3 4 5 $600 $400 $1, 041. 60 $ 573. 57 $ 62. 10 $1, 677. 27 = PV 0 (CF) $600(a 10%, 2) = $600(1. 736) = $1, 041. 60 $400(a 10%, 2)(v 10%, 2) = $400(1. 736)(0. 826) = $573. 57 $100 (v 10%, 5) = $100 (0. 621) = $62. 10 50

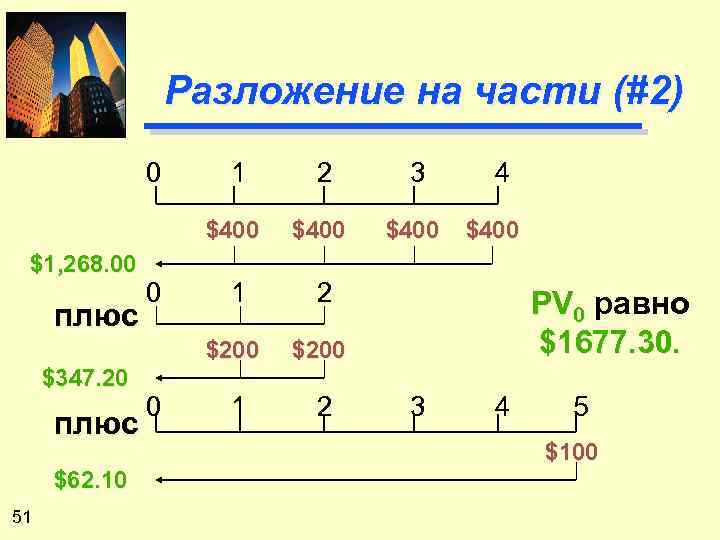
Разложение на части (#2) 0 плюс $347. 20 плюс $62. 10 51 0 3 $400 1 2 $200 0 2 $400 $1, 268. 00 1 $200 1 2 4 $400 PV 0 равно $1677. 30. 3 4 5 $100

Кратность начисления Общая формула: FVn = PV 0(1 + [i/m])mn n: Число лет m: Кратность начисления процентов в году i: Годовая процентная ставка FVn, m: Будущая стоимость через n лет PV 0: Текущая стоимость 52

Пример Вкладчик инвестирует $1000 на 2 года по ставке 12%. Годовое начисление процентов FV 2 = 1, 000(1+ [0. 12/1])(1)(2) 1, 000 = 1, 254. 40 Полугодовое начисление процентов FV 2 = 1, 000(1+ [0. 12/2])(2)(2) 1, 000 = 1, 262. 48 53

Эффект кратного начисления процентов Ежеквартально FV 2 = 1, 000(1+ [. 12/4])(4)(2) 1, 000 = 1, 266. 77 Ежемесячно FV 2 = 1, 000(1+ [. 12/12])(12)(2) 1, 000 = 1, 269. 73 Ежедневно FV 2 = 1, 000(1+[. 12/365])(365)(2) 1, 000 = 1, 271. 20 54

Эффективная годовая процентная ставка Эффективная годовая ставка Фактическая процентная ставка выплачиваемая по инвестициям с заданной номинальной ставкой с учетом кратности начисления процентов за год. ief =(1 + [ i / m ] )m - 1 55

Пример Инвестор вложил $1000 на депозит в банк. Ставка банка по депозитам 6% годовых с ежеквартальным начислением процентов. Какова эффективная ставка банка? Ief = ( 1 + 6% / 4 )4 - 1 = =1. 0614 - 1 = 0. 0614 или 6. 14%! 56

Схемы погашение долга 1. Определение погасительных платежей. 2. Определение процентов за период t. (остаток долга на момент t-1) (i% / m) 3. Определение основной части погасительного платежа за период t. (погасительный платеж проценты за период t. См. шаг 2) 4. Определение остатка невыплаченного долга на момент t. (Остаток на момент t -1 - основная часть погасительного платежа. См. шаг 3) 5. Возврат к началу шага 2. 57

Пример погашения долга Заемщик взял в кредит $10000 по сложной ставке 12% годовых. Рассчитать схему погашения долга если долг погашается одинаковыми годовыми платежами в течение 5 лет. Шаг 1: Погасительный платеж PV 0 = C (а i%, n) $10000 58 = C (а 12%, 5) = C (3. 605) C = $10000 / 3. 605 = $2774

Схема (график) погашения долга [последний платеж с небольшим округлением] 59

Использование схемы погашения долга 1. Определение процентных платежей -эти платежи могут уменьшать налоговые выплаты. 2. Определение остатка долга -- Остаток долга может использоваться для текущего финансирования 60