Financial Models 15 Zvi Wiener 02 -588 -3049

Financial Models 15 Zvi Wiener 02 -588 -3049 http: //pluto. mscc. huji. ac. il/~mswiener/zvi. html Jan-1999 T. Bjork, Arbitrage Theory in Continuous Time Foreign Currency, Bank of Israel

Bonds and Interest Rates Zero coupon bond = pure discount bond T-bond, denote its price by p(t, T). principal = face value, coupon bond - equidistant payments as a % of the face value, fixed and floating coupons. Zvi Wiener Fin. Models - 15 2

Assumptions F There exists a frictionless market for T- bonds for every T > 0 F p(t, t) =1 for every t F for every t the price p(t, T) is differentiable with respect to T. Zvi Wiener Fin. Models - 15 3

Interest Rates Let t < S < T, what is IR for [S, T]? F at time t sell one S-bond, get p(t, S) F buy p(t, S)/p(t, T) units of T-bond F cashflow at t is 0 F cashflow at S is -$1 F cashflow at T is p(t, S)/p(t, T) the forward rate can be calculated. . . Zvi Wiener Fin. Models - 15 4

The simple forward rate LIBOR - L is the solution of: The continuously compounded forward rate R is the solution of: Zvi Wiener Fin. Models - 15 5

Definition 15. 2 The simple forward rate for [S, T] contracted at t (LIBOR forward rate) is The simple spot rate for [S, T] LIBOR spot rate is Zvi Wiener Fin. Models - 15 6

Definition 15. 2 The continuously compounded forward rate for [S, T] contracted at t is The continuously compounded spot rate for [S, T] is Zvi Wiener Fin. Models - 15 7

Definition 15. 2 The instantaneous forward rate with maturity T contracted at t is The instantaneous short rate at time t is Zvi Wiener Fin. Models - 15 8

Definition 15. 3 The money market account process is Note that here t means some time moment in the future. This means Zvi Wiener Fin. Models - 15 9

Lemma 15. 4 For t s T we have And in particular Zvi Wiener Fin. Models - 15 10

Models of Bond Market F Specify the dynamic of short rate F Specify the dynamic of bond prices F Specify the dynamic of forward rates Zvi Wiener Fin. Models - 15 11

Important Relations Short rate dynamics dr(t)= a(t)dt + b(t)d. W(t) Bond Price dynamics (15. 1) (15. 2) dp(t, T)=p(t, T)m(t, T)dt+p(t, T)v(t, T)d. W(t) Forward rate dynamics df(t, T)= (t, T)dt + (t, T)d. W(t) (15. 3) W is vector valued Zvi Wiener Fin. Models - 15 12

Proposition 15. 5 We do NOT assume that there is no arbitrage! If p(t, T) satisfies (15. 2), then for the forward rate dynamics Zvi Wiener Fin. Models - 15 13

Proposition 15. 5 We do NOT assume that there is no arbitrage! If f(t, T) satisfies (15. 3), then the short rate dynamics Zvi Wiener Fin. Models - 15 14

Proposition 15. 5 If f(t, T) satisfies (15. 3), then the bond price dynamics Zvi Wiener Fin. Models - 15 15

Proof of Proposition 15. 5 Zvi Wiener Fin. Models - 15 16

Fixed Coupon Bonds Zvi Wiener Fin. Models - 15 17

Floating Rate Bonds L(Ti-1, Ti) is known at Ti-1 but the coupon is delivered at time Ti. Assume that K =1 and payment dates are equally spaced. Zvi Wiener Fin. Models - 15 18

This coupon will be paid at Ti. The value of -1 at time t is -p(t, Ti). The value of the first term is p(t, Ti-1). Zvi Wiener Fin. Models - 15 19

Forward Swap Settled in Arrears K - principal, R - swap rate, rates are set at dates T 0, T 1, … Tn-1 and paid at dates T 1, … Tn. T 0 Zvi Wiener T 1 Tn-1 Fin. Models - 15 Tn 20

Forward Swap Settled in Arrears If you swap a fixed rate for a floating rate (LIBOR), then at time Ti, you will receive where ci is a coupon of a floater. And at Ti you will pay the amount Net cashflow Zvi Wiener Fin. Models - 15 21

Forward Swap Settled in Arrears At t < T 0 the value of this payment is The total value of the swap at time t is then Zvi Wiener Fin. Models - 15 22

Proposition 15. 7 At time t=0, the swap rate is given by Zvi Wiener Fin. Models - 15 23

Zero Coupon Yield The continuously compounded zero coupon yield y(t, T) is given by For a fixed t the function y(t, T) is called the zero coupon yield curve. Zvi Wiener Fin. Models - 15 24

The Yield to Maturity The yield to maturity of a fixed coupon bond y is given by Zvi Wiener Fin. Models - 15 25

Macaulay Duration Definition of duration, assuming t=0. Zvi Wiener Fin. Models - 15 26

Macaulay Duration A weighted sum of times to maturities of each coupon. What is the duration of a zero coupon bond? Zvi Wiener Fin. Models - 15 27

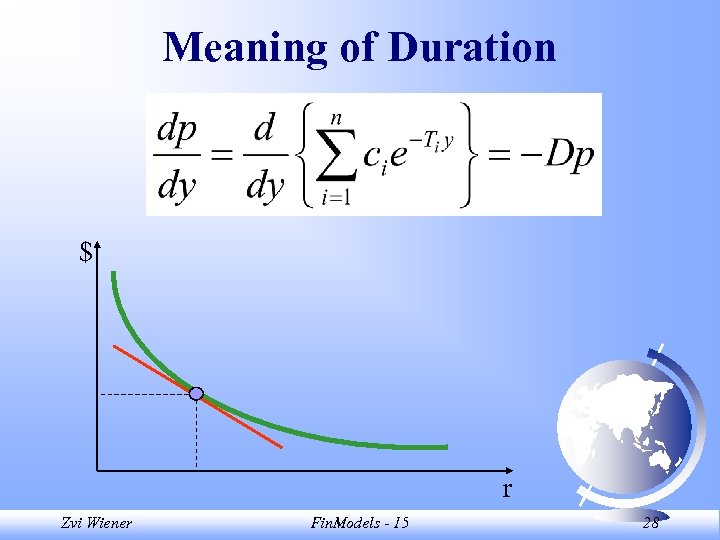Meaning of Duration $ r Zvi Wiener Fin. Models - 15 28

Proposition 15. 12 TS of IR With a term structure of IR (note yi), the duration can be expressed as: Zvi Wiener Fin. Models - 15 29

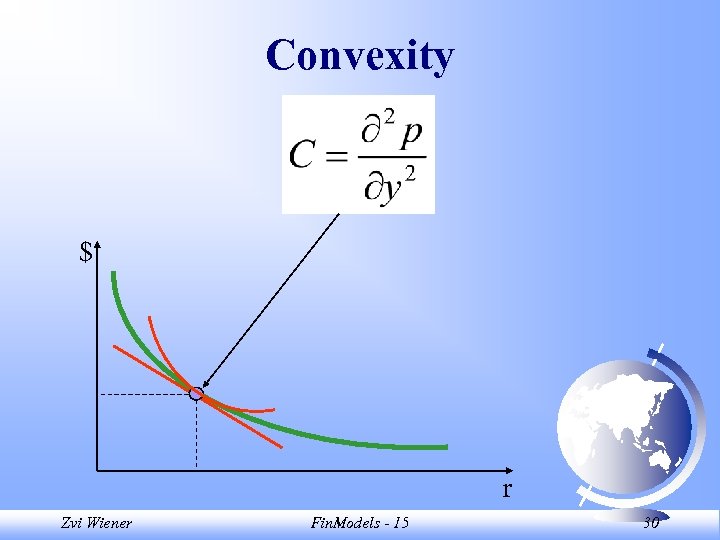Convexity $ r Zvi Wiener Fin. Models - 15 30

FRA Forward Rate Agreement A contract entered at t=0, where the parties (a lender and a borrower) agree to let a certain interest rate R*, act on a prespecified principal, K, over some future time period [S, T]. Assuming continuous compounding we have at time S: -K at time T: Ke. R*(T-S) Calculate the FRA rate R* which makes PV=0 hint: it is equal to forward rate Zvi Wiener Fin. Models - 15 31

Exercise 15. 7 Consider a consol bond, i. e. a bond which will forever pay one unit of cash at t=1, 2, … Suppose that the market yield is y - flat. Calculate the price of consol. Find its duration. Find an analytical formula for duration. Compute the convexity of the consol. Zvi Wiener Fin. Models - 15 32