d34a0688244094673a98b6b7e4772442.ppt
- Количество слайдов: 28

Fin I – SSE MBA Bond Prices and Yields 1

Bond Characteristics • Debt security issued by firms and government • Maturity • Face value (or par value) – Payment made to the BH at the maturity • Coupon rate – Annual interest payment made on the face value – Zero coupon bond: no coupons, but selling at a discount – Could be Fixed or Floating rate • Accrued interest – Prorated share of the upcoming coupon payment, which must be paid to the seller by buyer. Invoice price = quoted price + accrued interest 2

Bond Pricing T P B = å t =1 Ct T (1+ r ) + Par Value T T (1+ r ) Ct = T = PB = r = coupon payments number of periods to maturity Price of the bond (Present value of all future cash flows) yield to maturity (YTM) or discount rate (IRR earned from holding a bond to maturity) • There exists one-to-one correspondence between price and YTM – Given the value of one variable, we can solve for the other iteratively. – No compounding in converting semiannual YTM to an annual YTM (Also called the Bond Equivalent Yield) Cf. Effective annual yield ≥ Bond Equivalent Yield 3

Example: Compute price of 8% (semiannual), 10 -year with yield at 6% P B = 20 40 å (1. 03) t =1 t + 1, 000 20 (1. 03) = 1, 148. 77 = 40×Annuity factor(3, 20) + 1, 000×PV factor(3, 20) q Inputs for a financial calculator: FV Par Value = 1, 000 PMT Periodic payment = (8% / 2)× 1, 000 = 40 (Semiannual) i Periodic discount Rate = 6% / 2 = 3% (Semiannual) n Periods = 20 semiannual periods (10 years) PV = ? 4
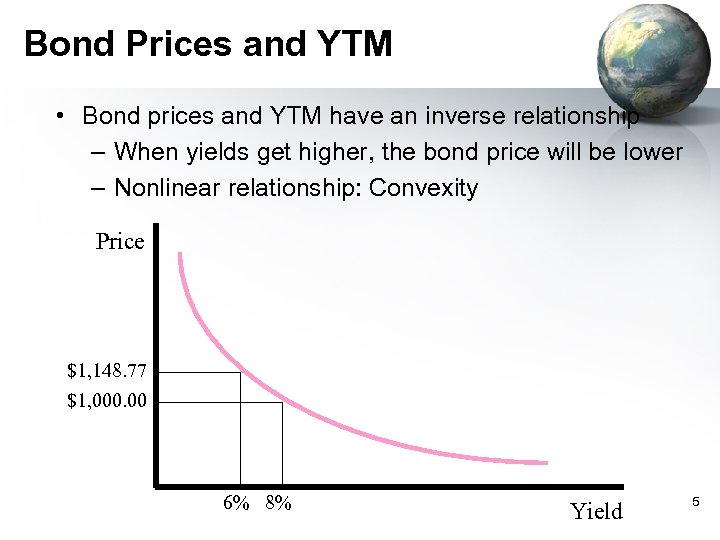
Bond Prices and YTM • Bond prices and YTM have an inverse relationship – When yields get higher, the bond price will be lower – Nonlinear relationship: Convexity Price $1, 148. 77 $1, 000. 00 6% 8% Yield 5
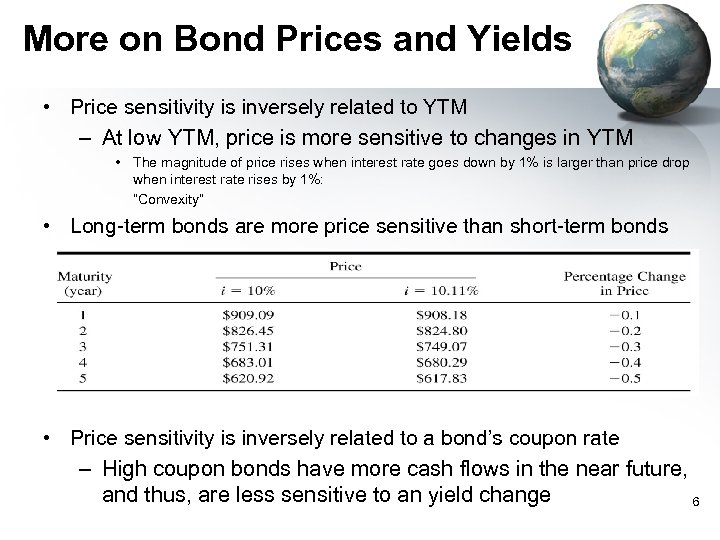
More on Bond Prices and Yields • Price sensitivity is inversely related to YTM – At low YTM, price is more sensitive to changes in YTM • The magnitude of price rises when interest rate goes down by 1% is larger than price drop when interest rate rises by 1%: “Convexity” • Long-term bonds are more price sensitive than short-term bonds • Price sensitivity is inversely related to a bond’s coupon rate – High coupon bonds have more cash flows in the near future, and thus, are less sensitive to an yield change 6

Selling at Premium or Discount • We say bonds are selling – At premium if coupon rate > yield-to-maturity • This means higher coupon than required, and thus, price > par • Bond price will decline over time to par value at maturity – At discount if coupon rate < yield-to-maturity • This means lower coupon than required, and thus, price < par • Bond price will increase over time to par value at maturity – At par if coupon rate = yield-to-maturity • Most of gov’t and corporate bonds are issued at par E. g. , coupon = yield-to-maturity – Depending on the market interest movement, YTM changes, and thus, may be selling at premium or discount 7

Price Path of Premium or Discount Bonds over Time Price Premium Bond Par value Discount Bond 0 Time to Maturity 8

Other Measures of Yield • Current Yield = Annual coupon / bond price Yield to maturity = current yield + capital gain yield • Yield-to-Call – Callable bonds are likely to be called as the interest rate falls – Taking this into account, yield for callable bond is calculated by replacing the maturity with the time until the call is first possible, and replacing the par value with call price • Bank Discount Rate – Applies to Treasury bills or short-term money market instruments (Ex) If 90 -day T-bill is selling at $9, 875, its discount rate is, [(10, 000 – 9, 875) / 10, 000 ] × (360 / 90) = 5% Converting this into bond equivalent yield gives, [(10, 000 – 9, 875) / 9, 875 ] × (365 / 90) = 5. 13% 9

Default Risk and Bond Ratings • (Stated) YTM will be realized if the firm survives – If the firm defaults, investors cannot get the state yield – Therefore, default risk premium is included in the yield, e. g. , YTM = riskfree rate + default premium + liquidity premium +. . . • Default risk is classified into categories by bond rating companies – Standard & Poor’s, Moody’s, Fitch, etc. – Investment grade: AAA ~ BBB Speculative grade (or junk bond): BB or below • Key determinants of bond ratings – – – Interest coverage ratio = EBIT / Interest payment Leverage ratio = Debt / Equity Liquidity ratio = Current assets / current liabilities Profitability ratio: ROA = Net income / Assets Cash flow to debt = Cash flow / Debt 10
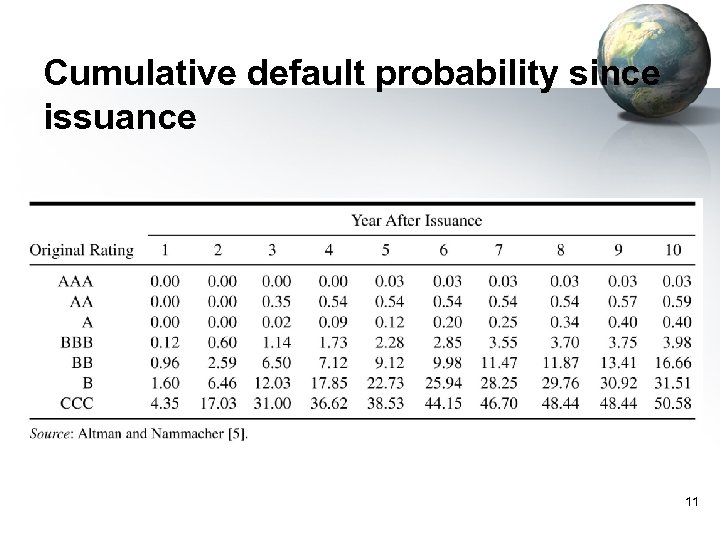
Cumulative default probability since issuance 11

Innovations in the Bond Market • Floating rate bonds (Floaters) – Coupon rates are periodically reset to a reference rate (EX) Coupon rate = reference rate (LIBOR) + credit spread where credit spread is generally fixed at time of issue by issuer – Less sensitive to interest movements than straight bond. Why? • Reverse Floaters (EX) Coupon rate = 15% – reference rate – More sensitive to interest movements than straight bond. Why? • Asset-backed bonds or Mortgage-backed bonds • Indexed bonds – TIPS (Treasury Inflation Protected Securities) • Coupon rates are adjusted to the realized inflation rate 12

Various Provisions of Bonds • Secured or unsecured • Call provision – Allows the issuer to redeem the bond before maturity at a prespecified call price – Used to replace an existing bond with a new one at a lower coupon – Investors must be compensated for this provision with higher yields • Put provision (putable bonds) – Allows BH to retire the bond before maturity at a par value • Convertible provision – Allows BHs to exchange the bond for common stocks – Suppose a CB is selling at par of $1, 000, convertible into 40 shares If current stock price is $30, then is it profitable to convert? • conversion ratio = 40 (shares) • conversion value = $30 × 40 shares = $1, 200 • conversion premium = $1, 000 - $1, 200 = -$200 13

Term Structure of Interest Rates • Relationship between YTM and maturity – Also called “Yield curve” • Plot of yields on bonds for different maturities • Zero yield curve, Forward curve, etc. – Yields on the same graph must have similar risk. Otherwise, other factors could influence the yields • Usually, yield curve for Treasury Bonds (risk-free) becomes the basis of all other bonds – In general, yield curve looks upward sloping, i. e. , higher yields for longer-term bonds, but sometimes, it slopes downward. 14
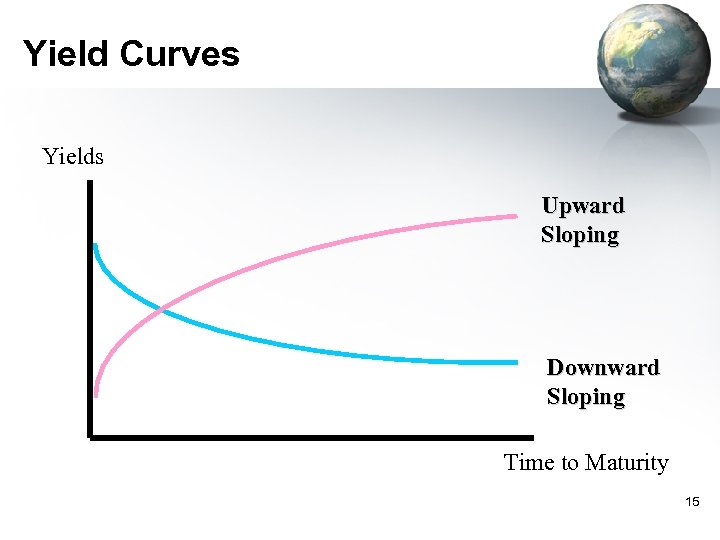
Yield Curves Yields Upward Sloping Downward Sloping Time to Maturity 15

Theories of Term Structure • What determines the shape of a yield curve? • Pure Expectations Hypothesis – Upward slope means that the market is expecting higher future short term rates, and vice versa (1+y 2)2 = (1+y 1)[1+ E(1 r 2)] and 1 f 2 = E(1 r 2) • Liquidity Preference Hypothesis – Long-term bonds have greater uncertainty for short-term holding (1+y 2)2 = (1+y 1)[1+ E(1 r 2)+ 1 L 2 ] and 1 f 2 = E(1 r 2) + 1 L 2 • Market Segmentation Hypothesis – Each investor has a preferred maturity for the purpose of matching maturities of assets and liabilities • Banks prefer short-term maturity bonds, whereas insurance firms prefer longer-term maturity bonds 16

Forward Rates Implied (1+ y n ) q q q n = (1+ n -1 y n -1) (1 + n-1 fn ) yn = spot rate = YTM on zero coupon bonds whose interest applies from now to maturity n-1 fn = forward rate = YTM on zero coupon bonds whose interest applies from a future date to maturity For example, if a 1 -year spot rate is 11% and 2 -year spot rate is 12%, then forward rate is calculated as (1+0. 12)2 = (1+0. 11)(1+ 1 f 2) 1 f 2 = (1+0. 12)2 / (1+0. 11) – 1 = 13. 01% q In general, k-period implied forward rate is n n-k – 1 n-kfn = (1+yn) / (1+yn-k) 17

Credit Spreads • Yield difference between corporate bonds and T-bonds with the same maturity – Spreads tend to increase with maturity and with a decrease in rating 18
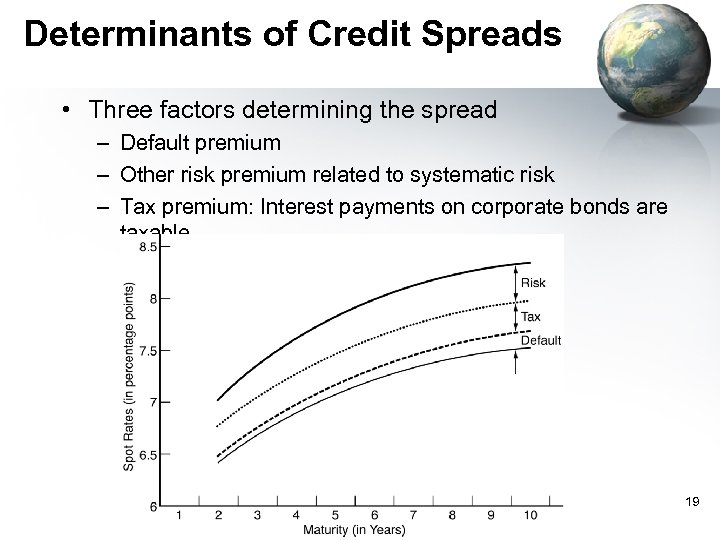
Determinants of Credit Spreads • Three factors determining the spread – Default premium – Other risk premium related to systematic risk – Tax premium: Interest payments on corporate bonds are taxable 19

Duration • A comprehensive measure of interest rate risk – Useful in hedge or immunization strategies • A measure of the effective maturity of a bond – The weighted average of the times until each payment is received, with the weights proportional to the present value of the payment T D = å t × wt t =1 where wt = [CFt / (1+y)t ] / Price • Duration is shorter than maturity for all coupon bonds, and equals maturity for zero coupon bonds – For a perpetuity, D = (1+y) / y = (1+0. 1)/0. 1= 11 years 20
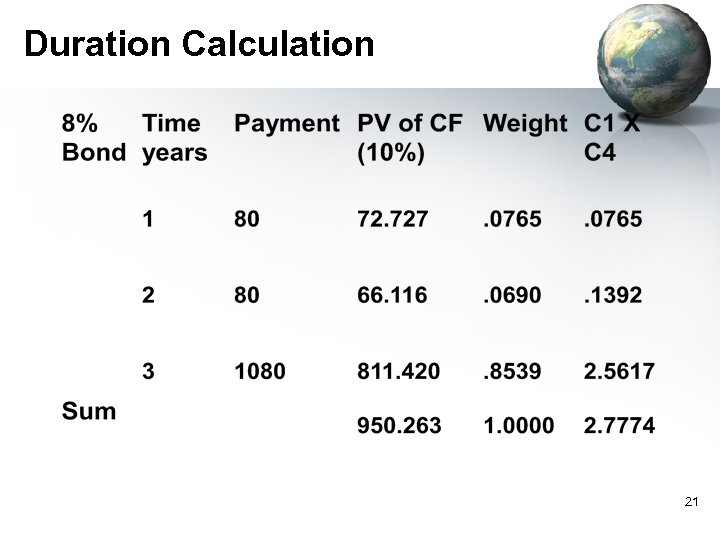
Duration Calculation 21

Duration and Price Relationship • Price change is proportional to duration and not to maturity DP/P = -D x [D(1+y) / (1+y)] Or, using the modified duration, Dm = D / (1+y), DP/P = - Dm x Dy – Therefore, once we know the values of D and y, then we can calculate DP/P for a given change in y 22
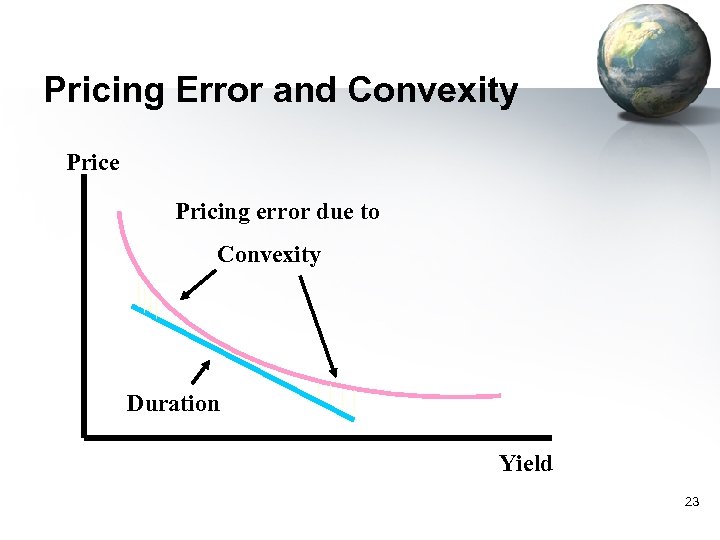
Pricing Error and Convexity Price Pricing error due to Convexity Duration Yield 23

Correction for Convexity Approximate the bond price by Taylor series expansion DP = - D × D y + 1 ×Convexity × ( D y ) 2 2 P Convexity is calculated as: N 1 P× (1 + y) 2 å t =1 é CF t ù 2 + t )ú ê t (t ë (1 + y ) û Where: CFt is the cashflow (interest and/or principal) at time t. 24

Bond Portfolio Management • Passive strategies – Buy-and-hold – Indexing – Immunization • Barbell vs. bullet strategies – Cash flow matching (or dedication in multi-period) • Match cash flow exactly by buying a zero-coupon bond against cash flows of your liability • Active strategies – Bond swap – Horizon analysis – Contingent immunization 25
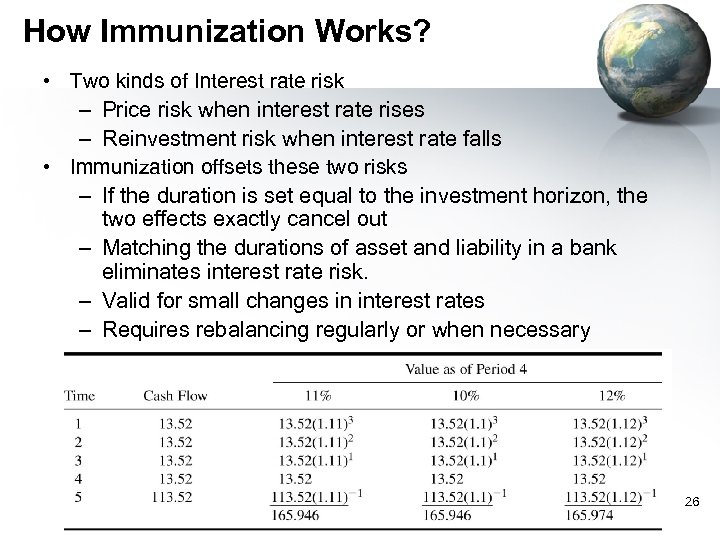
How Immunization Works? • Two kinds of Interest rate risk – Price risk when interest rate rises – Reinvestment risk when interest rate falls • Immunization offsets these two risks – If the duration is set equal to the investment horizon, the two effects exactly cancel out – Matching the durations of asset and liability in a bank eliminates interest rate risk. – Valid for small changes in interest rates – Requires rebalancing regularly or when necessary 26

Example: Immunization • An insurance company – Liability: Payment of $19, 487 in seven years – Asset: The fund manager decides to hold (1) 3 -year zero-coupon bond, and (2) Perpetuity (Assume market interest rate = 10%) <Solve the portfolio weights for immunization> – Duration of liability = 7 years – Duration of a portfolio = weighted average of duration of assets in the portfolio = w× 3 + (1–w)× 11 (duration of the perpetuity = (1+0. 1)/0. 1 = 11 years) – Match the portfolio duration to 7 years: w× 3 + (1–w)× 11 = 7 w = 0. 5 (3 -yr zero), and (1 -w)=0. 5 (perpetuity) • After one year, do you have to rebalance it to maintain the immunization strategy? (assume interest rate is still 10%) What should be the new weights for each asset? 27

Swaps • Bond swaps – Substitution swap – Intermarket swap – Rate anticipation swap – Yield pick-up swap – Tax swap • Interest rate swap – Exchange of interest streams (fixed vs. floating) without exchanging the bond itself 28
d34a0688244094673a98b6b7e4772442.ppt