FIN 30220 Macroeconomic Analysis Long Run Growth

FIN 30220: Macroeconomic Analysis Long Run Growth

The World Economy n n n Total GDP (2013): $87 T Population (2013): 7. 1 B GDP per Capita (2013): $13, 100 Population Growth (2013): 1. 0% GDP Growth (2013): 2. 9% GDP per capita is probably the best measure of a country’s overall well being

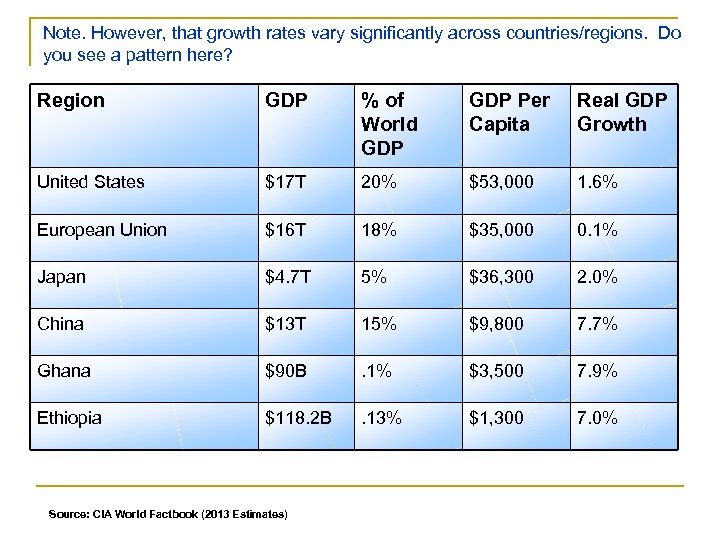Note. However, that growth rates vary significantly across countries/regions. Do you see a pattern here? Region GDP % of World GDP Per Capita Real GDP Growth United States $17 T 20% $53, 000 1. 6% European Union $16 T 18% $35, 000 0. 1% Japan $4. 7 T 5% $36, 300 2. 0% China $13 T 15% $9, 800 7. 7% Ghana $90 B . 1% $3, 500 7. 9% Ethiopia $118. 2 B . 13% $1, 300 7. 0% Source: CIA World Factbook (2013 Estimates)

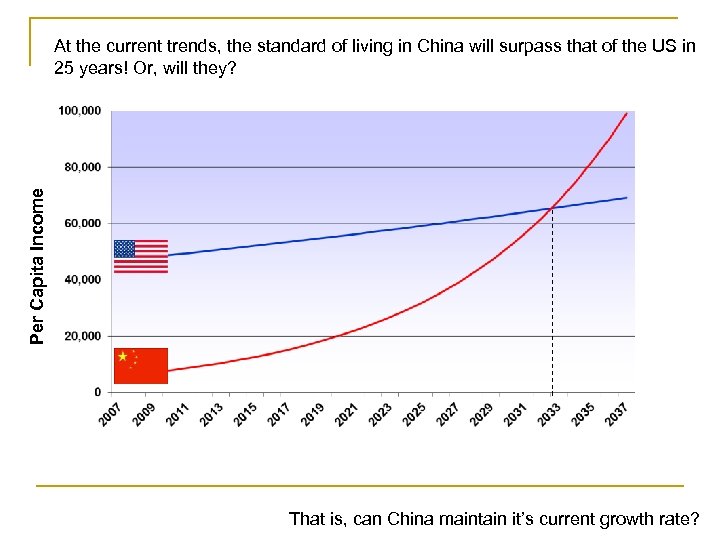Per Capita Income At the current trends, the standard of living in China will surpass that of the US in 25 years! Or, will they? That is, can China maintain it’s current growth rate?

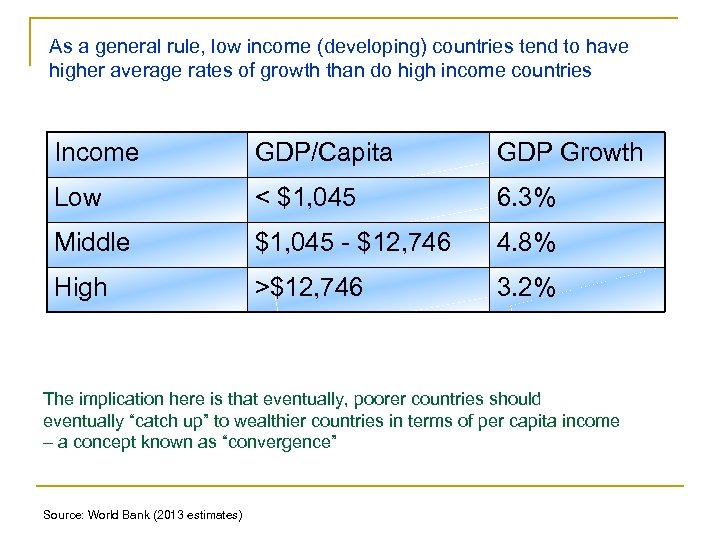As a general rule, low income (developing) countries tend to have higher average rates of growth than do high income countries Income GDP/Capita GDP Growth Low < $1, 045 6. 3% Middle $1, 045 - $12, 746 4. 8% High >$12, 746 3. 2% The implication here is that eventually, poorer countries should eventually “catch up” to wealthier countries in terms of per capita income – a concept known as “convergence” Source: World Bank (2013 estimates)

Some countries, however, don’t fit the normal pattern of development Sudan GDP: $107 B (#73) GDP Per Capita: $5, 100 (#159) GDP Growth: -2. 3% (#213) Macau GDP: $51. 6 B (#98) GDP Per Capita: $88, 700 (#3) GDP Growth: 11. 9% (#5) At current trends, Per capita income in Macau will triple to $273, 000 over the next decade. Over the same time period, per capita GDP in Sudan will drop by roughly 25%to $4, 000!!! So, what is Sudan doing wrong? (Or, what is Macau doing right? )

To understand this, let’s look at the sources of economic growth…. where does production come from? “is a function of” Real GDP Productivity Capital Stock Labor Real GDP = Constant Dollar (Inflation adjusted) value of all goods and services produced in the United States Capital Stock = Constant dollar value of private, non-residential fixed assets Labor = Private Sector Employment Productivity = Production unaccounted for by capital or labor

A convenient functional form for growth accounting is the Cobb-Douglas production function. It takes the form: where With the Cobb-Douglas production function, the parameters have clear interpretations: Capital’s share of income (what % of total income in the US accrues to owners of capital) Labor’s share of income (what % of total income in the US accrues to owners of labor) Elasticity of output with respect to capital (% increase in output resulting from a 1% increase in capital) Elasticity of output with respect to labor (% increase in output resulting from a 1% increase in labor)

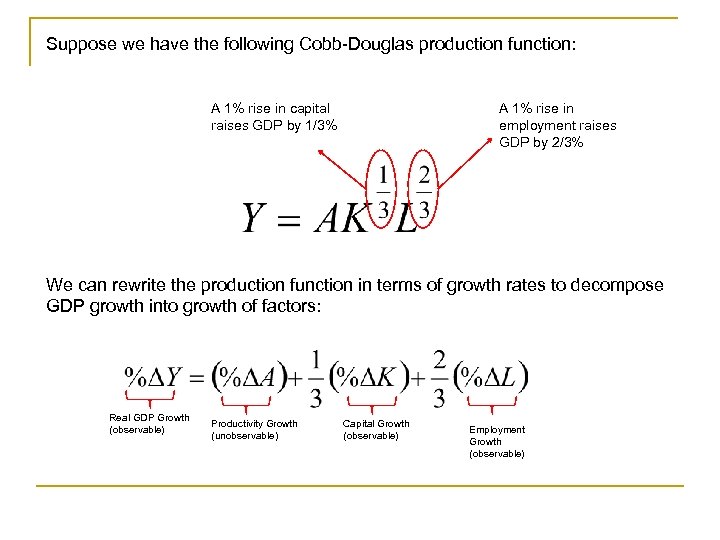Suppose we have the following Cobb-Douglas production function: A 1% rise in capital raises GDP by 1/3% A 1% rise in employment raises GDP by 2/3% We can rewrite the production function in terms of growth rates to decompose GDP growth into growth of factors: Real GDP Growth (observable) Productivity Growth (unobservable) Capital Growth (observable) Employment Growth (observable)

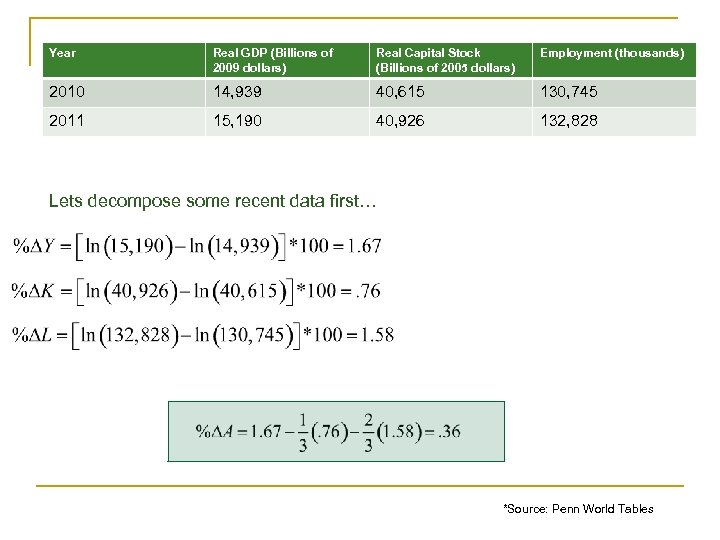Year Real GDP (Billions of 2009 dollars) Real Capital Stock (Billions of 2005 dollars) Employment (thousands) 2010 14, 939 40, 615 130, 745 2011 15, 190 40, 926 132, 828 Lets decompose some recent data first… *Source: Penn World Tables

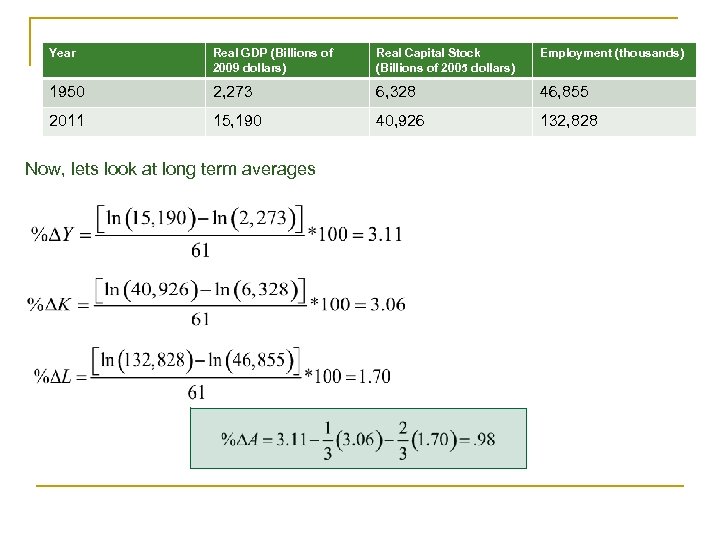Year Real GDP (Billions of 2009 dollars) Real Capital Stock (Billions of 2005 dollars) Employment (thousands) 1950 2, 273 6, 328 46, 855 2011 15, 190 40, 926 132, 828 Now, lets look at long term averages

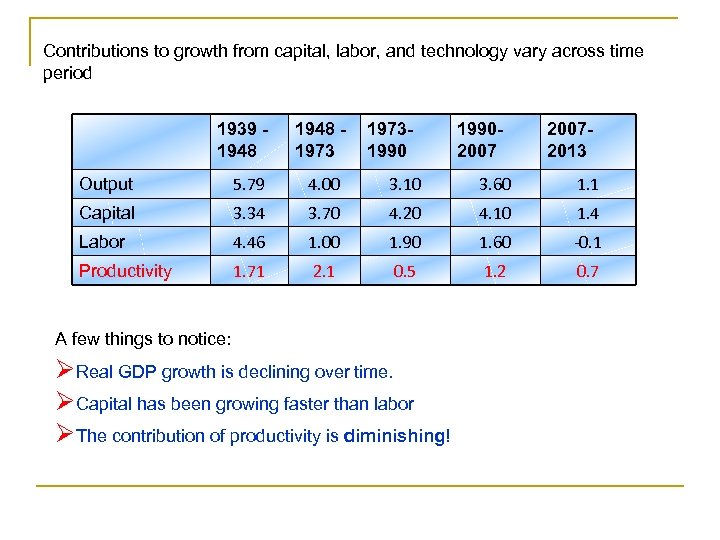Contributions to growth from capital, labor, and technology vary across time period 1939 1948 1973199020072013 Output 5. 79 4. 00 3. 10 3. 60 1. 1 Capital 3. 34 3. 70 4. 20 4. 10 1. 4 Labor 4. 46 1. 00 1. 90 1. 60 -0. 1 Productivity 1. 71 2. 1 0. 5 1. 2 0. 7 A few things to notice: ØReal GDP growth is declining over time. ØCapital has been growing faster than labor ØThe contribution of productivity is diminishing!

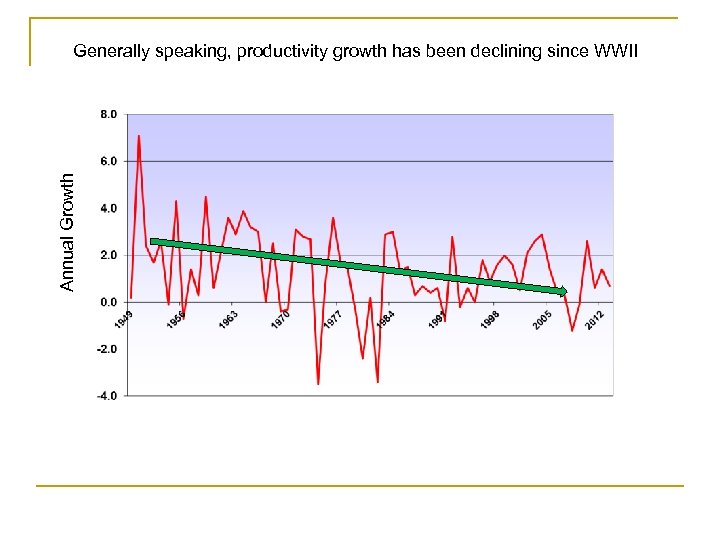Annual Growth Generally speaking, productivity growth has been declining since WWII

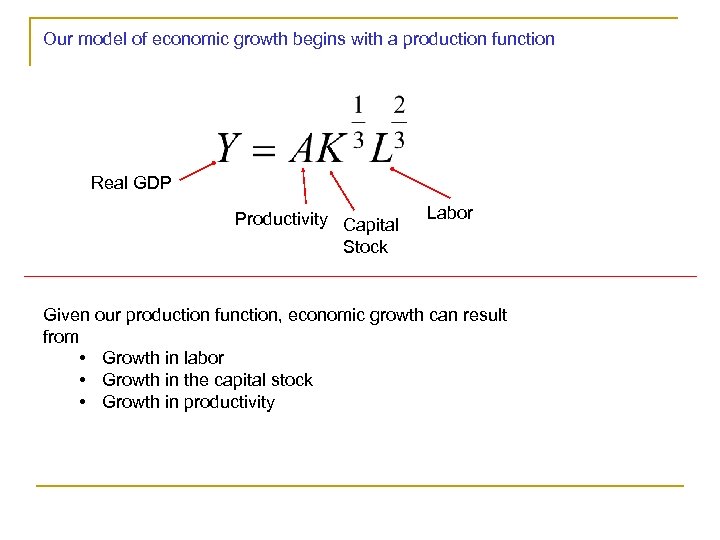Our model of economic growth begins with a production function Real GDP Productivity Capital Stock Labor Given our production function, economic growth can result from • Growth in labor • Growth in the capital stock • Growth in productivity

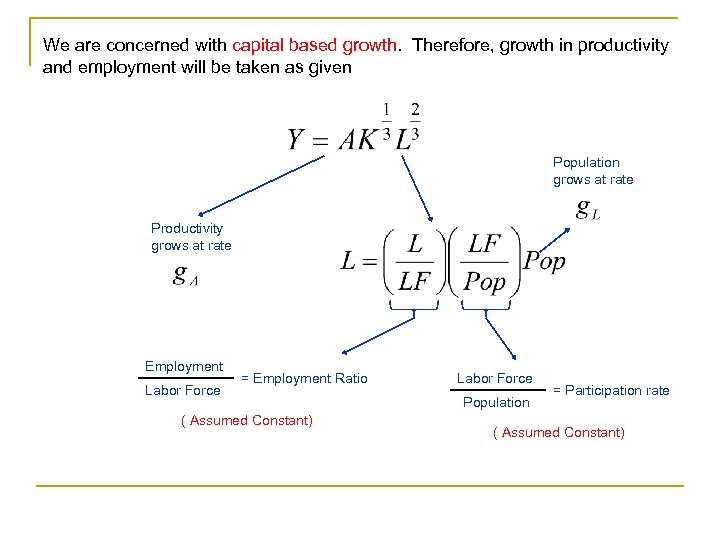We are concerned with capital based growth. Therefore, growth in productivity and employment will be taken as given Population grows at rate Productivity grows at rate Employment Labor Force = Employment Ratio ( Assumed Constant) Labor Force Population = Participation rate ( Assumed Constant)

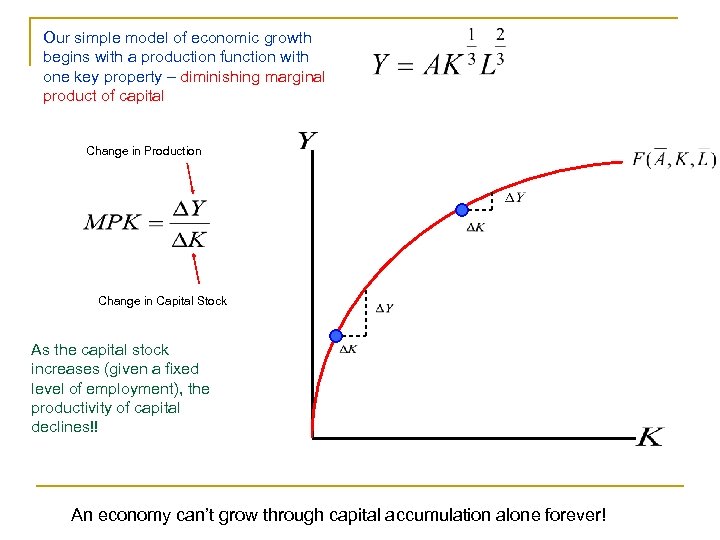Our simple model of economic growth begins with a production function with one key property – diminishing marginal product of capital Change in Production Change in Capital Stock As the capital stock increases (given a fixed level of employment), the productivity of capital declines!! An economy can’t grow through capital accumulation alone forever!

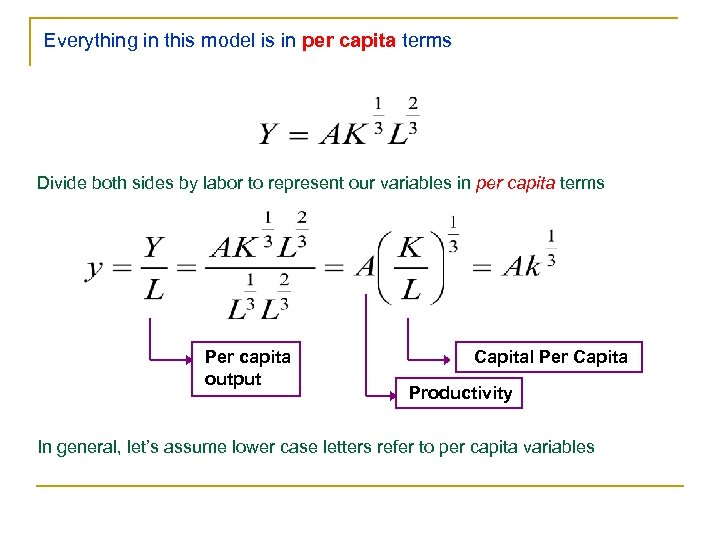Everything in this model is in per capita terms Divide both sides by labor to represent our variables in per capita terms Per capita output Capital Per Capita Productivity In general, let’s assume lower case letters refer to per capita variables

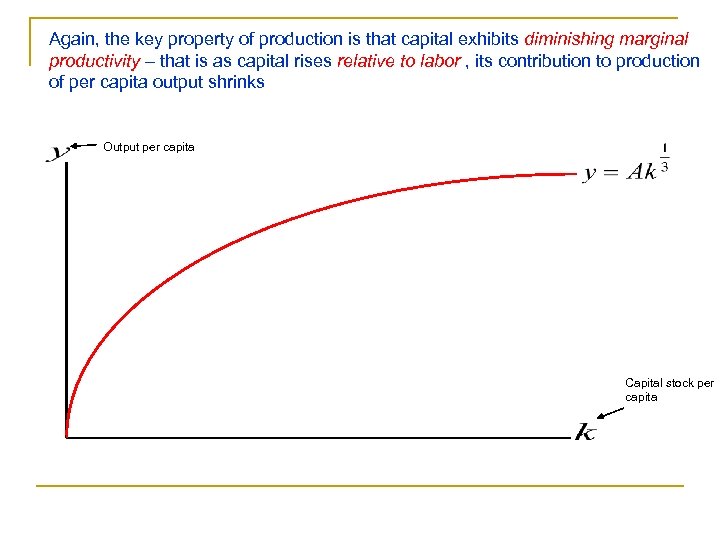Again, the key property of production is that capital exhibits diminishing marginal productivity – that is as capital rises relative to labor , its contribution to production of per capita output shrinks Output per capita Capital stock per capita

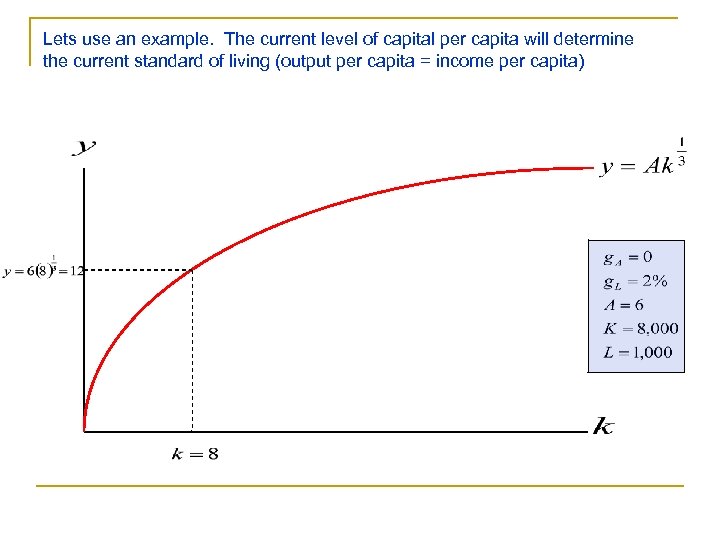Lets use an example. The current level of capital per capita will determine the current standard of living (output per capita = income per capita)

Next, assume that households save a constant fraction of their disposable income Income Less Taxes Savings Constant between zero and one Again, convert everything to per capital terms by dividing through by the labor force

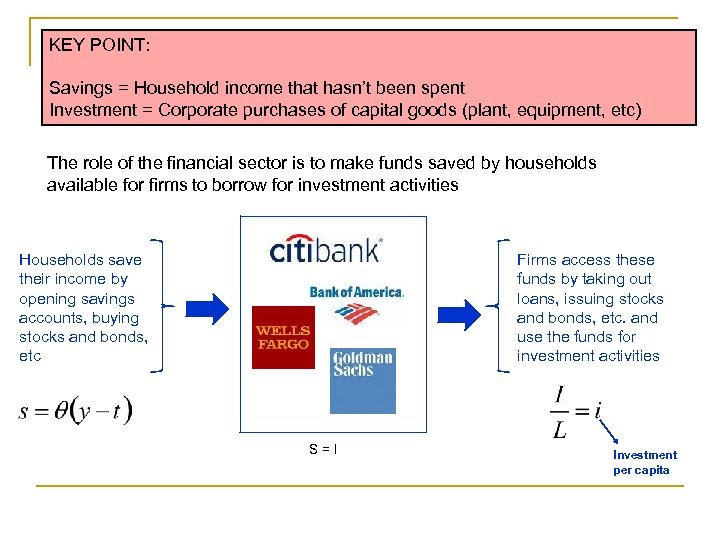KEY POINT: Savings = Household income that hasn’t been spent Investment = Corporate purchases of capital goods (plant, equipment, etc) The role of the financial sector is to make funds saved by households available for firms to borrow for investment activities Households save their income by opening savings accounts, buying stocks and bonds, etc Firms access these funds by taking out loans, issuing stocks and bonds, etc. and use the funds for investment activities S=I Investment per capita

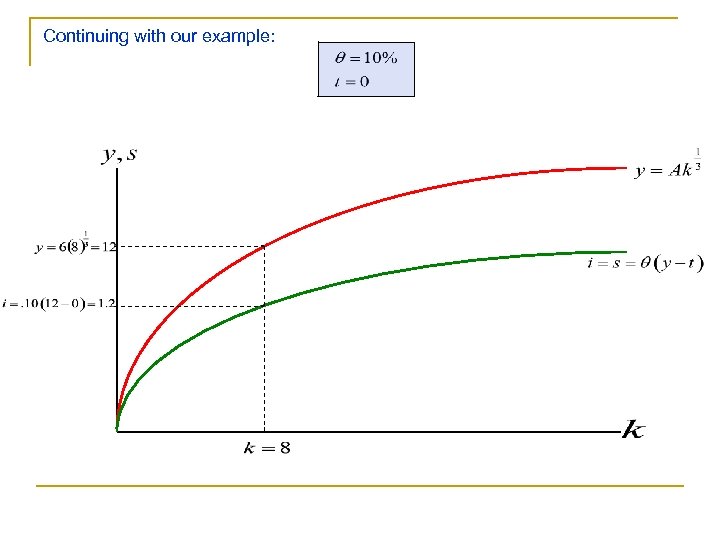Continuing with our example:

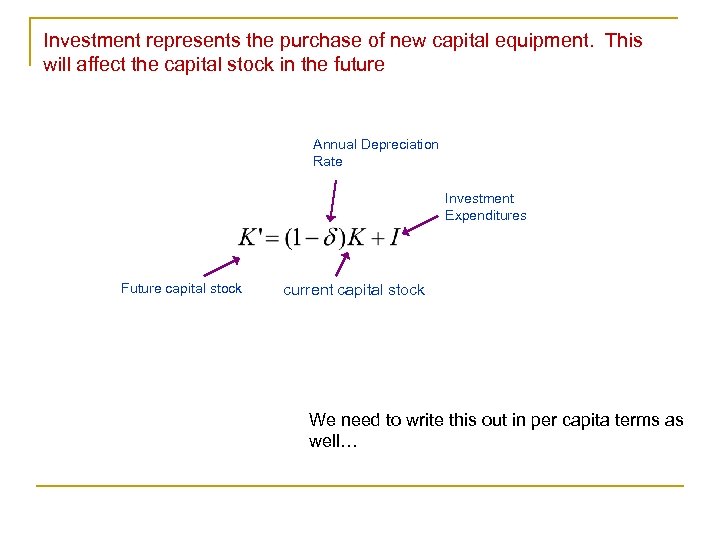Investment represents the purchase of new capital equipment. This will affect the capital stock in the future Annual Depreciation Rate Investment Expenditures Future capital stock current capital stock We need to write this out in per capita terms as well…

We need to write this out in per capita terms as well… Divide through by labor to get things in per capita terms Multiply and divide the left hand side by future labor supply Recall that labor grows at a constant rate

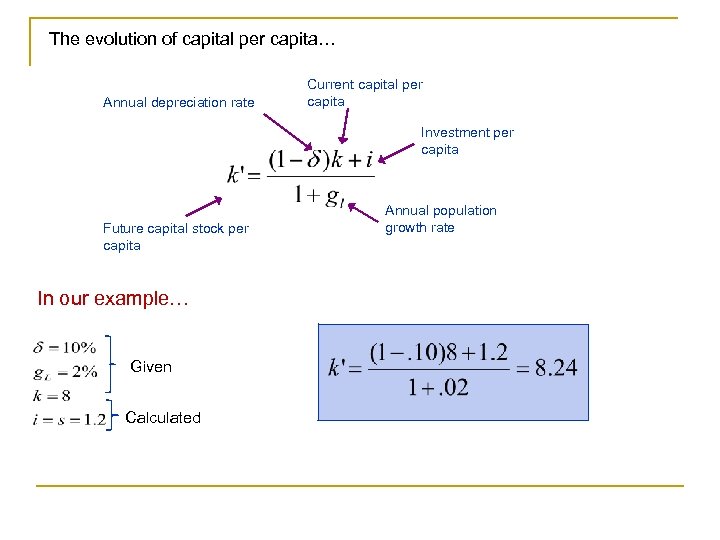The evolution of capital per capita… Annual depreciation rate Current capital per capita Investment per capita Future capital stock per capita In our example… Given Calculated Annual population growth rate

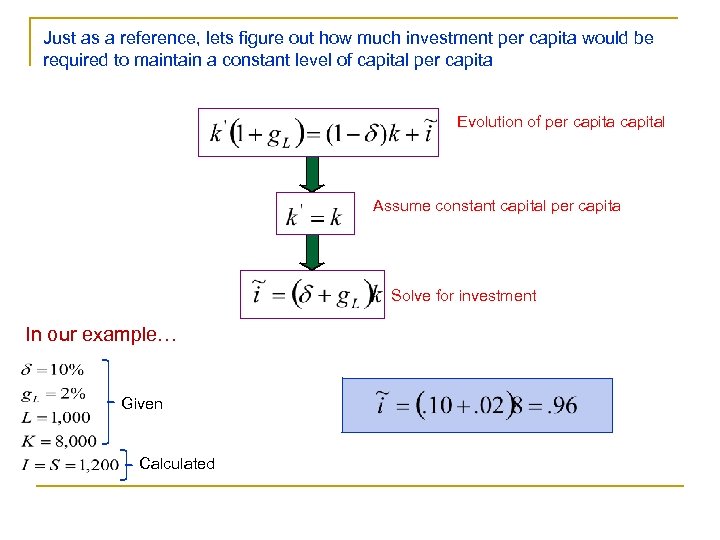Just as a reference, lets figure out how much investment per capita would be required to maintain a constant level of capital per capita Evolution of per capital Assume constant capital per capita Solve for investment In our example… Given Calculated

Just to make sure, lets check our numbers… In our example… The evolution of capital per capita…

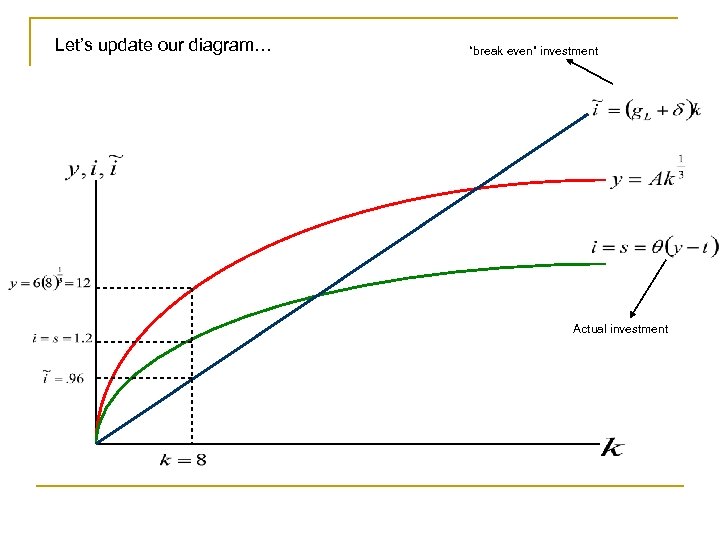Let’s update our diagram… “break even” investment Actual investment

Now we have all the components to calculate next years output per capita and the rate of growth Given Calculated Output per capita growth

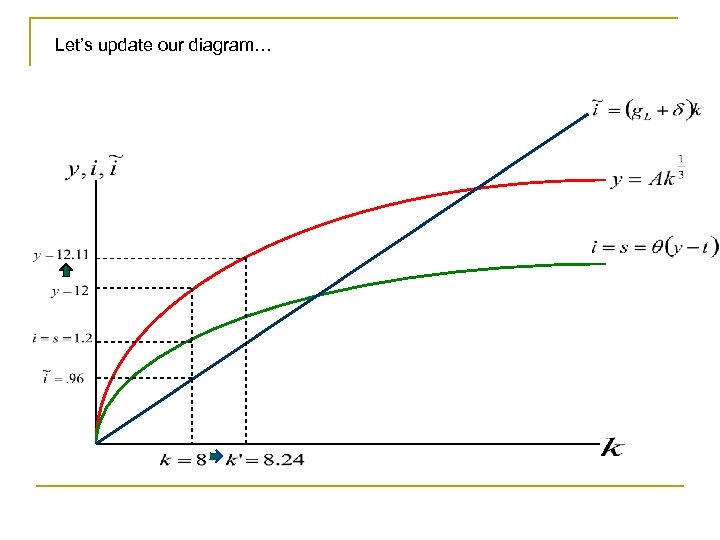Let’s update our diagram…

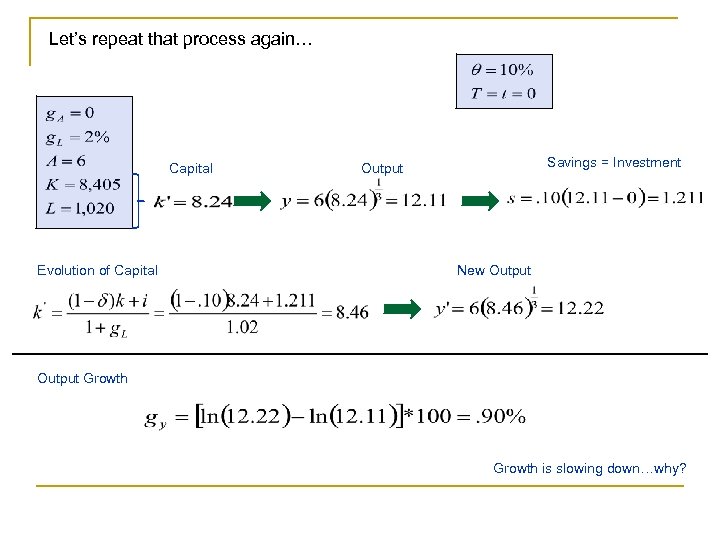Let’s repeat that process again… Capital Evolution of Capital Savings = Investment Output New Output Growth is slowing down…why?

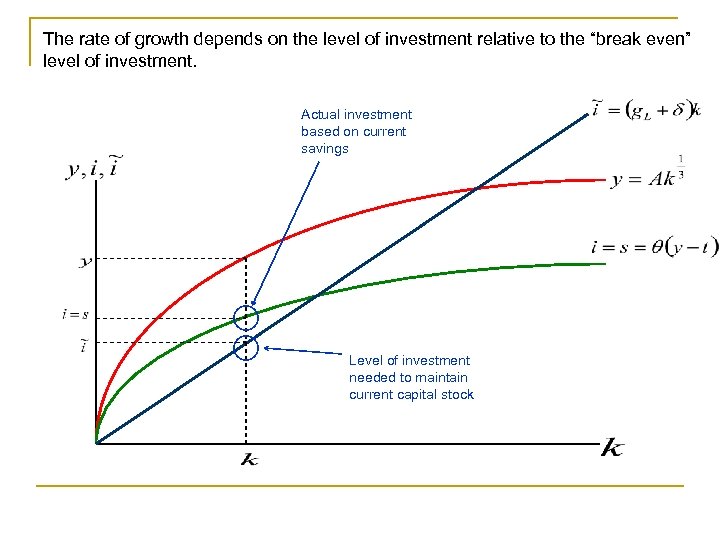The rate of growth depends on the level of investment relative to the “break even” level of investment. Actual investment based on current savings Level of investment needed to maintain current capital stock

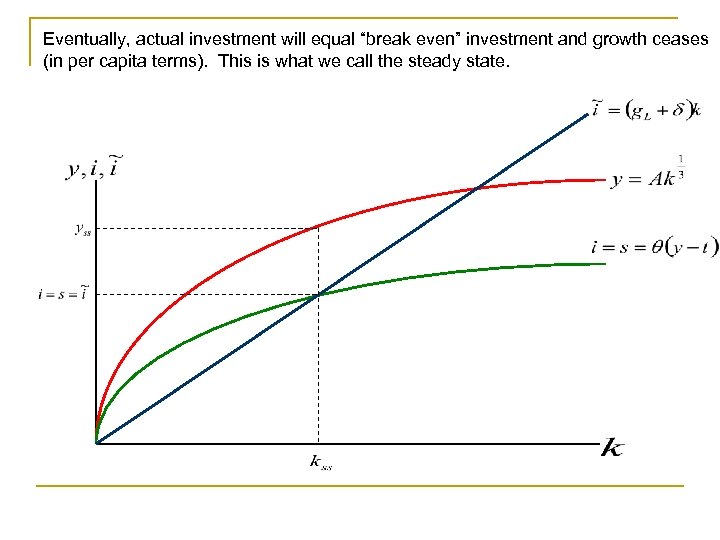Eventually, actual investment will equal “break even” investment and growth ceases (in per capita terms). This is what we call the steady state.

The steady state has three conditions…. 2 1 Savings per capita is a constant fraction of output per capita Output is a function of capital per capita 3 Investment is sufficient to maintain a constant capital/labor ratio Recall that, in equilibrium, savings equals investment

With a little algebra, we can solve for the steady state in our example. Start with condition 3 Use condition 2 and the fact that savings equals investment Substitute condition 1 Recall that taxes are zero in our example Solve for k

Plugging in our parameters gives us steady state values. Steady state per capital Steady state per capita output Steady state per capita savings/investment Steady state per capita consumption Constant per capital!!!

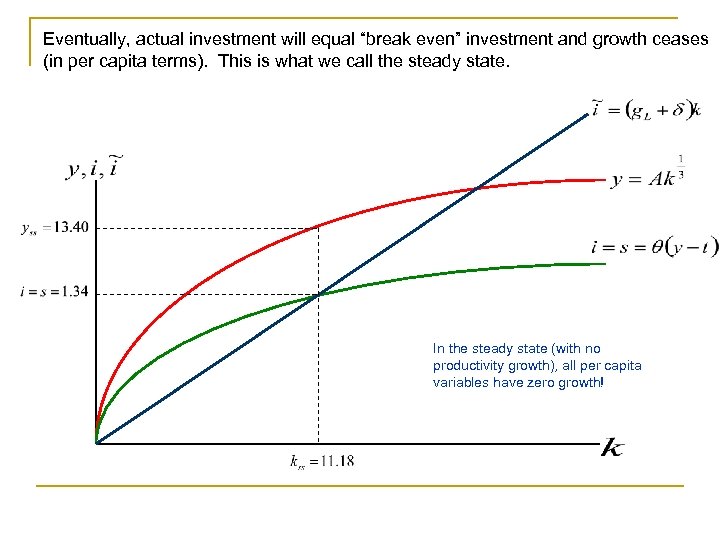Eventually, actual investment will equal “break even” investment and growth ceases (in per capita terms). This is what we call the steady state. In the steady state (with no productivity growth), all per capita variables have zero growth!

Suppose we started out example economy above it’s eventual steady state… An economy above its steady state shrinks (in per capita terms) towards its steady state.

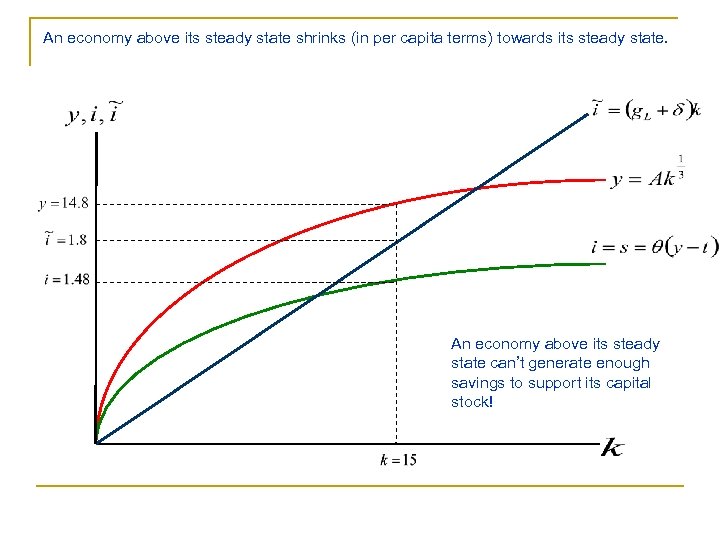An economy above its steady state shrinks (in per capita terms) towards its steady state. An economy above its steady state can’t generate enough savings to support its capital stock!

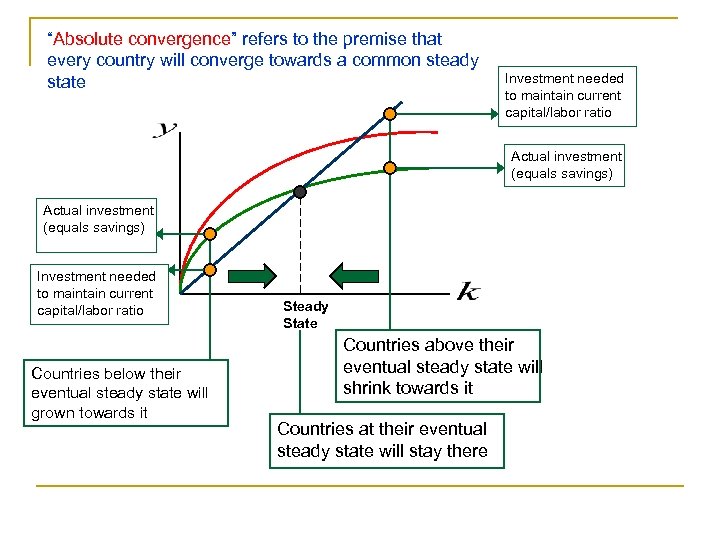“Absolute convergence” refers to the premise that every country will converge towards a common steady state Investment needed to maintain current capital/labor ratio Actual investment (equals savings) Investment needed to maintain current capital/labor ratio Countries below their eventual steady state will grown towards it Steady State Countries above their eventual steady state will shrink towards it Countries at their eventual steady state will stay there

Most countries follow the “usual” pattern of development 1 Developing countries have very little capital, but A LOT of labor. Hence, the price of labor is low, the return to capital is very high 2 High returns to capital attract a lot of investment. As the capital stock grows relative to the labor force, output, consumption, and real wages grow while interest rates (returns to capital fall) 3 Eventually, a country “matures” (i. e. reaches its steady state level of capital). At this point, growth can no longer be achieved by investment in capital. Growth must be “knowledge based” – improving productivity! Productivity

Does the economy have a “speed limit”? Economic Growth can be broken into three components: GDP = Productivity Growth + (2/3)Labor Growth + (1/3)Capital Growth In the Steady State, Capital Growth = Labor Growth GDP Growth = Productivity Growth + Labor Growth ( GDP Per Capita Growth = Productivity Growth)

Developing countries are well below their steady state and, hence should grow faster than developed countries who are at or near their steady states – a concept known as absolute convergence Examples of Absolute Convergence (Developing Countries) China (GDP per capita = $6, 300, GDP Growth = 9. 3%) Armenia (GDP per capita = $5, 300, GDP Growth = 13. 9%) Chad (GDP per capita = $1, 800, GDP Growth = 18. 0%) Angola (GDP per capita = $3, 200, GDP Growth = 19. 1%) Examples of Absolute Convergence (Mature Countries) Canada (GDP per capita = $32, 900, GDP Growth = 2. 9%) United Kingdom (GDP per capita = $30, 900, GDP Growth = 1. 7%) Japan (GDP per capita = $30, 700, GDP Growth = 2. 4%) Australia (GDP per capita = $32, 000, GDP Growth = 2. 6%)

Some countries, however, don’t fit the traditional pattern. Developing Countries with Low Growth Madagascar(GDP per capita = $900, GDP Growth = - 2. 0%) Iraq (GDP per capita = $3, 400, GDP Growth = - 3. 0%) North Korea (GDP per capita = $1, 800, GDP Growth = 1. 0%) Haiti (GDP per capita = $1, 200, GDP Growth = -5. 1%) Developed Countries with high Growth Hong Kong (GDP per capita = $37, 400, GDP Growth = 6. 9%) Iceland (GDP per capita = $34, 900, GDP Growth = 6. 5%) Singapore (GDP per capita = $29, 900, GDP Growth = 5. 7%) Qatar (GDP Per Capita = $179, 000, GDP Growth = 16. 3%)

Consider two countries… Country A Country B We already calculated this! Even though Country B is poorer, it is growing slower than country A (in per capita terms)!

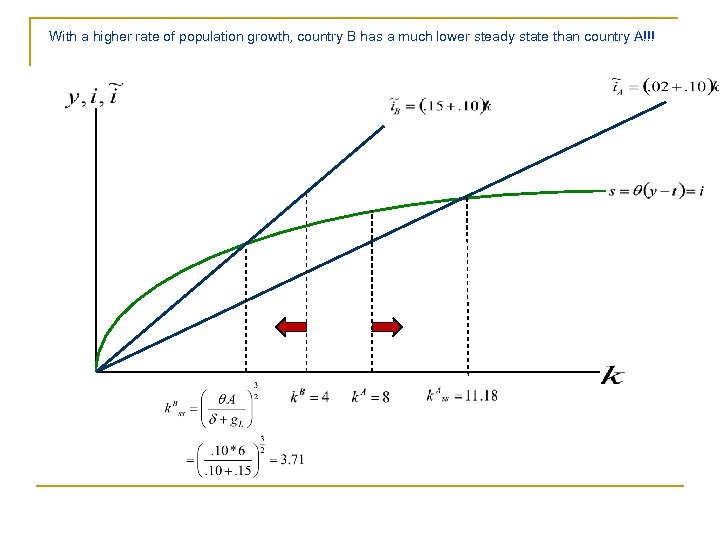With a higher rate of population growth, country B has a much lower steady state than country A!!!

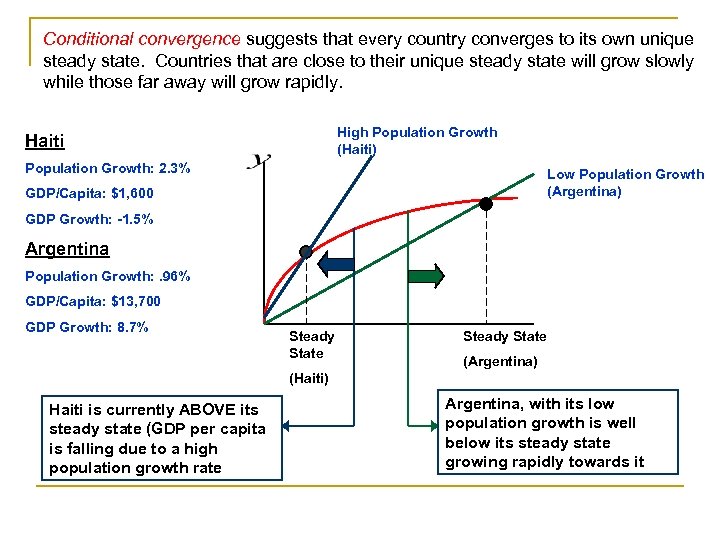Conditional convergence suggests that every country converges to its own unique steady state. Countries that are close to their unique steady state will grow slowly while those far away will grow rapidly. High Population Growth (Haiti) Haiti Population Growth: 2. 3% Low Population Growth (Argentina) GDP/Capita: $1, 600 GDP Growth: -1. 5% Argentina Population Growth: . 96% GDP/Capita: $13, 700 GDP Growth: 8. 7% Steady State (Argentina) (Haiti) Haiti is currently ABOVE its steady state (GDP per capita is falling due to a high population growth rate Argentina, with its low population growth is well below its steady state growing rapidly towards it

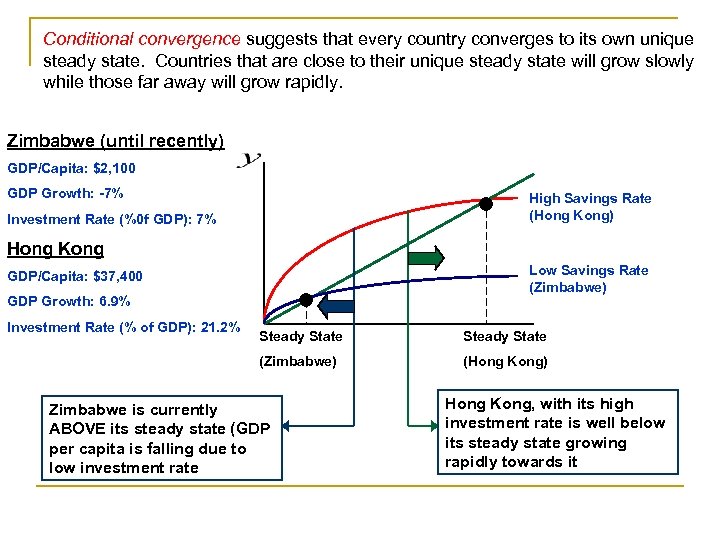Conditional convergence suggests that every country converges to its own unique steady state. Countries that are close to their unique steady state will grow slowly while those far away will grow rapidly. Zimbabwe (until recently) GDP/Capita: $2, 100 GDP Growth: -7% High Savings Rate (Hong Kong) Investment Rate (%0 f GDP): 7% Hong Kong Low Savings Rate (Zimbabwe) GDP/Capita: $37, 400 GDP Growth: 6. 9% Investment Rate (% of GDP): 21. 2% Steady State (Zimbabwe) (Hong Kong) Zimbabwe is currently ABOVE its steady state (GDP per capita is falling due to low investment rate Hong Kong, with its high investment rate is well below its steady state growing rapidly towards it

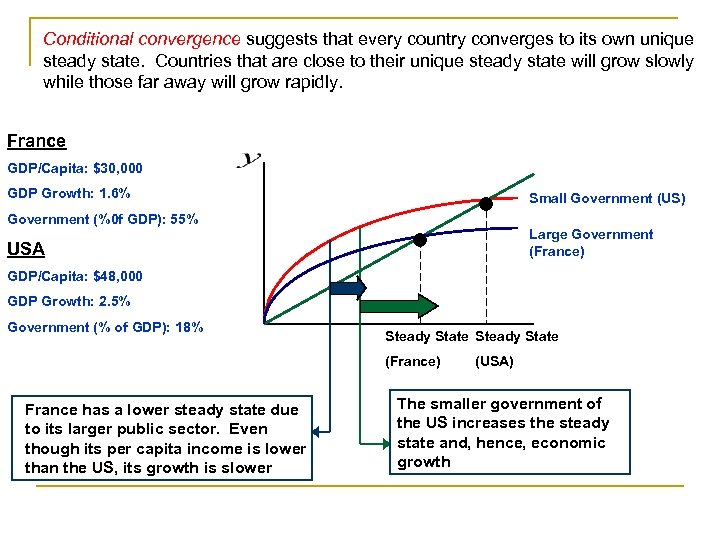Conditional convergence suggests that every country converges to its own unique steady state. Countries that are close to their unique steady state will grow slowly while those far away will grow rapidly. France GDP/Capita: $30, 000 GDP Growth: 1. 6% Small Government (US) Government (%0 f GDP): 55% Large Government (France) USA GDP/Capita: $48, 000 GDP Growth: 2. 5% Government (% of GDP): 18% Steady State (France) France has a lower steady state due to its larger public sector. Even though its per capita income is lower than the US, its growth is slower (USA) The smaller government of the US increases the steady state and, hence, economic growth

Suggestions for growth…. High income countries with low growth are at or near their steady state. Policies that increase capital investment will not be useful due to the diminishing marginal product of capital. ØConsider investments in technology and human capital to increase your steady state. ØConsider limiting the size of your government to shift resources to more productive uses (efficiency vs. equity) Low income countries with low growth either have a low steady state or are having trouble reaching their steady state ØConsider policies to lower your population growth. ØTry to increase your pool of savings (open up to international capital markets) ØPolicies aimed at capital formation (property rights, tax credits, etc).

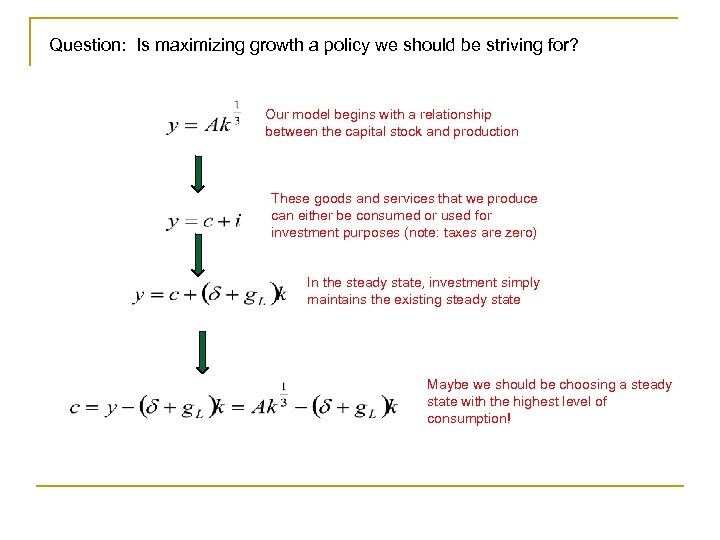Question: Is maximizing growth a policy we should be striving for? Our model begins with a relationship between the capital stock and production These goods and services that we produce can either be consumed or used for investment purposes (note: taxes are zero) In the steady state, investment simply maintains the existing steady state Maybe we should be choosing a steady state with the highest level of consumption!

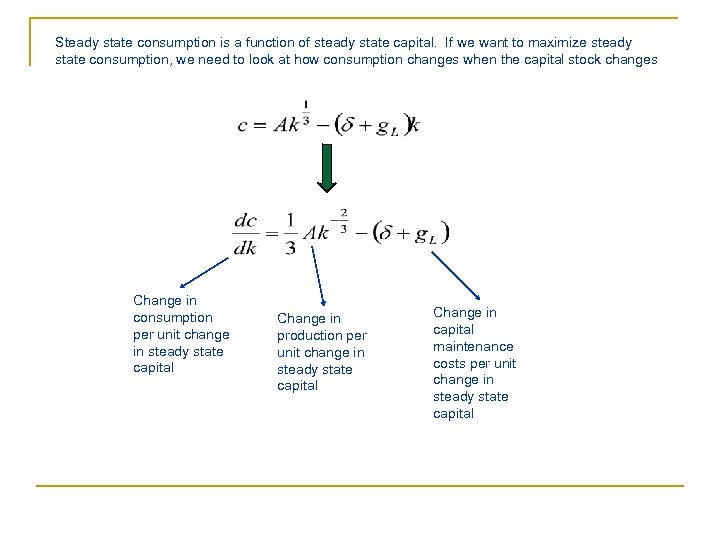Steady state consumption is a function of steady state capital. If we want to maximize steady state consumption, we need to look at how consumption changes when the capital stock changes Change in consumption per unit change in steady state capital Change in production per unit change in steady state capital Change in capital maintenance costs per unit change in steady state capital

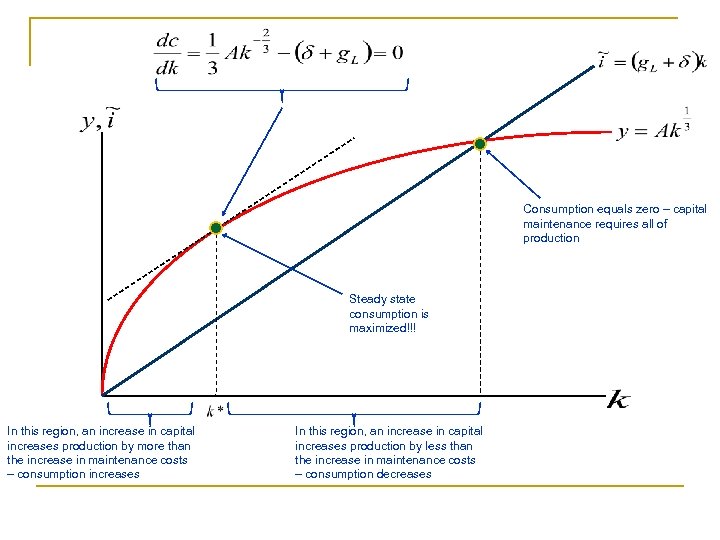Consumption equals zero – capital maintenance requires all of production Steady state consumption is maximized!!! In this region, an increase in capital increases production by more than the increase in maintenance costs – consumption increases In this region, an increase in capital increases production by less than the increase in maintenance costs – consumption decreases

Let’s go back to our example… We can solve for the steady state capital that maximizes consumption

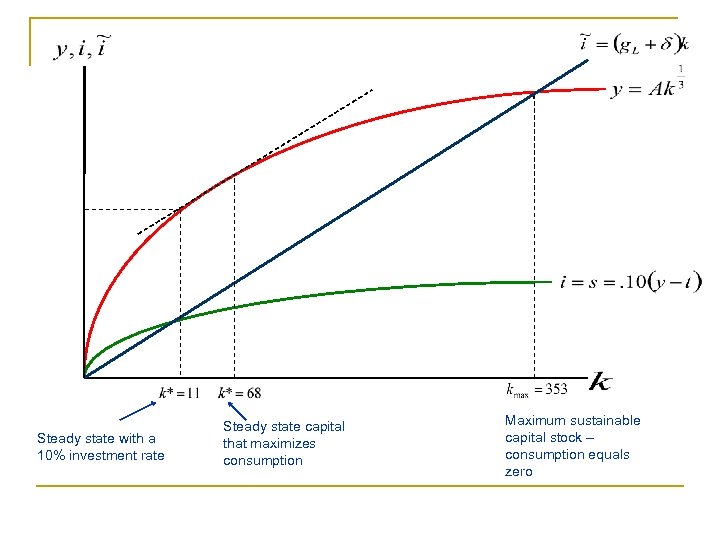Steady state with a 10% investment rate Steady state capital that maximizes consumption Maximum sustainable capital stock – consumption equals zero

Using our example, lets compare consumption levels… Steady State with Savings Rate = 10% “Optimal” Steady State In this example, we could increase consumption by 30% by altering the savings rate!!

By comparing steady states, we can find the savings rate associated with maximum consumption Steady State with a given Savings Rate “Optimal” Steady State To maximize steady state consumption, we need a 33% savings/investment rate!!