Filter-Diagonalization 1 Matrix Diagonalization Quantum Dynamics circumventing

Filter-Diagonalization 1. Matrix Diagonalization & Quantum Dynamics: circumventing 2. Signal Processing! 3. Examples: Experimental signals Semiclassical: [Trajectory-dependent cellularization (traj. -dep. Filinov)] QMC (DMC)

Groups interested in extracting eigenstates (or Density. Matrices) using “filters” Mandelshtam, Shaka, Chen (Irvine) Taylor (USC) Baer (Jerusalem) (Density-Matrices) Rabani (Tel-Aviv) (Density-Matrices) Wyatt (Houston) Head-Gordon (Berkeley) (Density-Matrices) Moiseyev (Haifa) Guo (New-Mexico) Meyer, Cederbaum, Beck (Heidelberg) Ruchman&Gershgoren, Labview implementation for condensed phases signals (Jerusalem) D. N. , Mike Wall, Johnny Pang, Sybil Anderson, Jaejin Ka Emily Carter, Antonio, de Silva, E. Fattal, Peter Felker, Julie Feigon, Wousik Kim(UCLA)

Existing Approaches for eigenstates: Non-sepearable H: Lowest state: ITERATE. General: LANCOSZ H Tridiagonal Eigenvalues simple for REAL H’s Converges fastest near gaps. Too democratic.

Filter-Diagonalization: Extends FFT Bridges FFT and other approaches, Trick: Connect Q. M. Signal Processing Signal processing can be recast (mapped) as a QM problem.

To see connection: start from QM. H given, need Simplest approach: FFT C(t). Expensive! Need long time to resolve closely-spaced eigenvalues

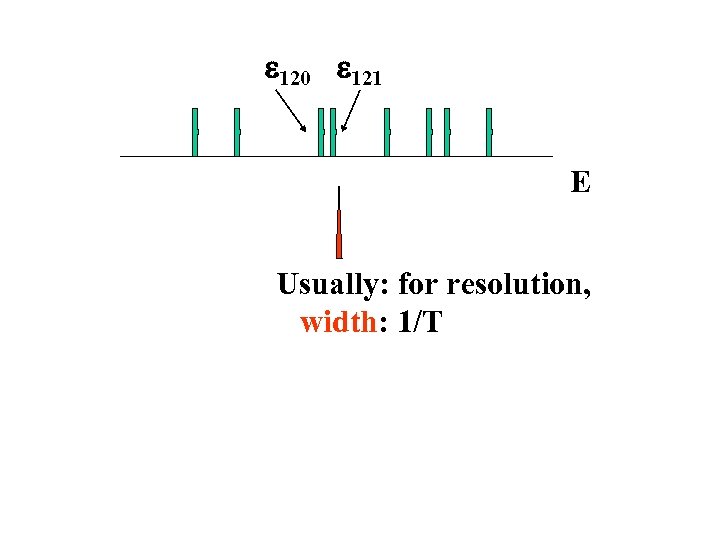e 120 e 121 E Usually: for resolution, width: 1/T

Filter-Diagonalization: 1) Filter the same w. p. at 2 (or more) energies Resulting in energy-localized states, even if T is short!

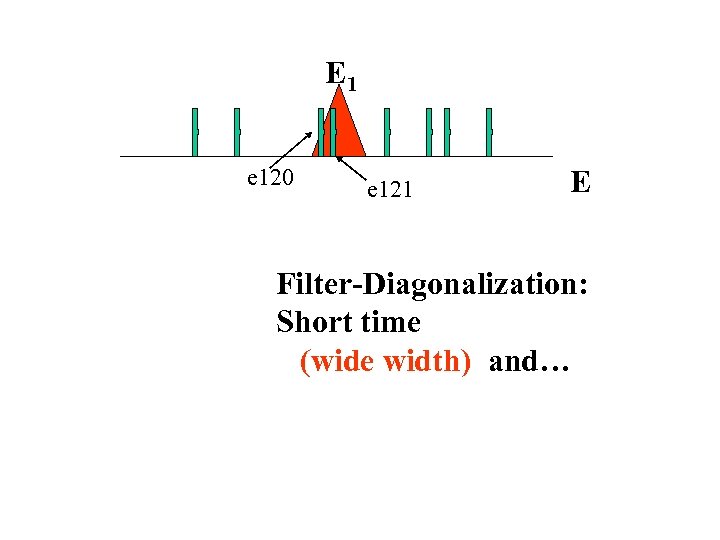E 1 e 120 e 121 E Filter-Diagonalization: Short time (wide width) and…

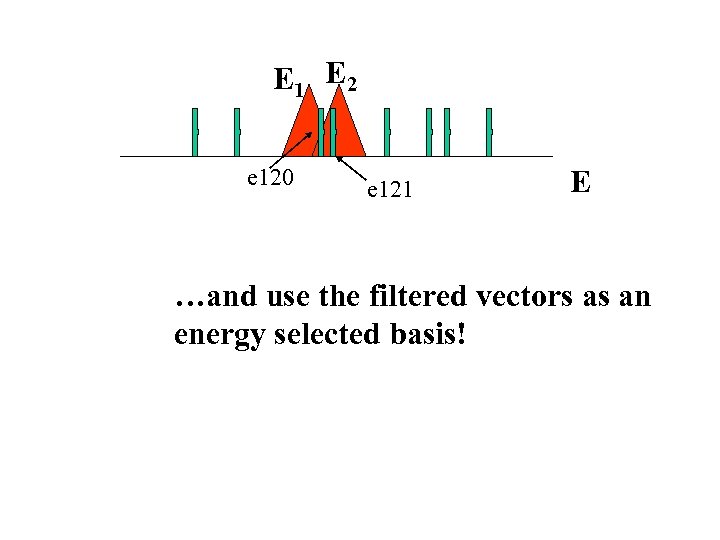E 1 E 2 e 120 e 121 E …and use the filtered vectors as an energy selected basis!

Practically: • Orthogonalize • Diagonalize small matrix.

Filter – short time throws contribution of most eigenstates. Diagonalization: separates contribution of closely-spaced eigenvalues.

Method: as is useful for extracting eigenstates From a short time filter; Or in general diagonalizing matrices in selected energy ranges (Especially if multiple initial vectors are used).

Combined Approach: First: Then: Orthogonalize the Finally: diagonalize the small matrix:

Time-dependent propagation. First: general methods: Spectral Propagation: Split-Operator:

Pre-conditioning+Filter-Diagonalization: (Wyatt; Carrington) Pre-conditioning: H=H 0+V Basis-set localized around Ej ! Diagonalize H in basis

DFT: Divide and Conquer Renormalization Group—Baer and Head-Gordon. D: concentrated around m, so just few e. functions are enough.

Surprising feature of Filter-Diagonalization: can be recast as a: Signal processing application!

And now to : Signal Processing: From C(t) t=0, dt, 2 dt, 3 dt, …, T Get all t C(t) OR:

Signal Processing: Not trivial. 1) “Classical” “MUSIC”, Linear-Prediction, Maximum-Entropy: work usually increases for long signals 2) FFT: • Handles easily long signals. But: • Handles only a single signal at a time • Long propagation time

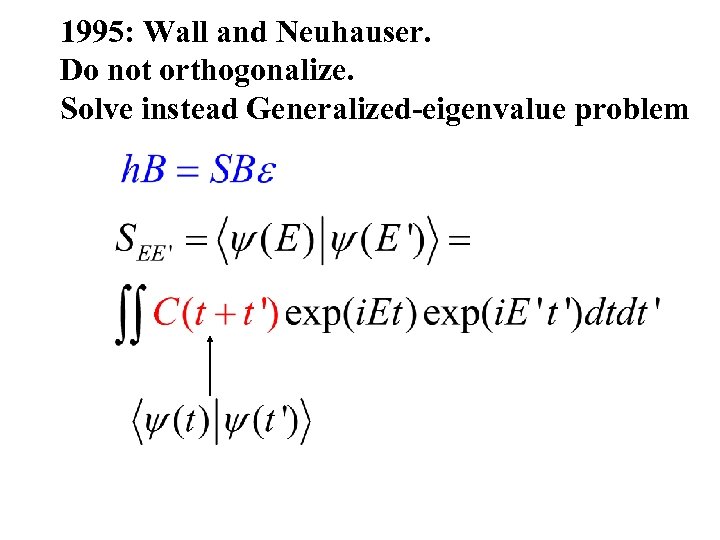1995: Wall and Neuhauser. Do not orthogonalize. Solve instead Generalized-eigenvalue problem

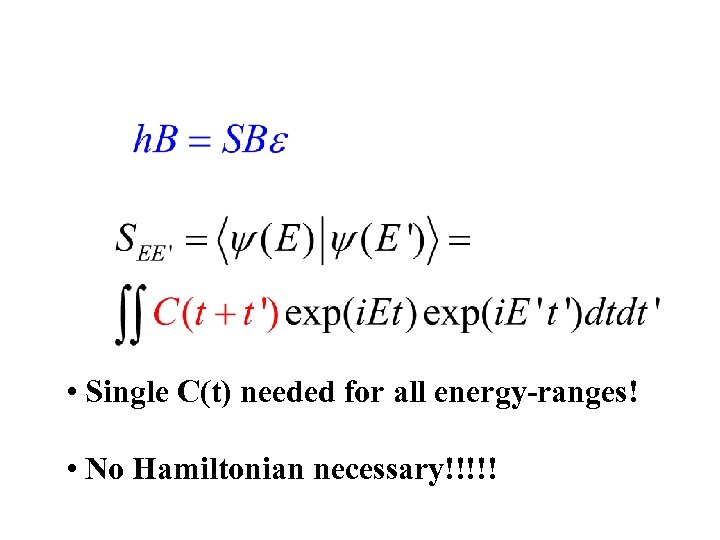• Single C(t) needed for all energy-ranges! • No Hamiltonian necessary!!!!!

Route “eventual”: H Eigenvalues from C(t) H not needed (need not exist) Route “completed”: Eigenvalues from C(t)

Sig. Proc. Algorithm (automated): Choose frequency range Choose # of vectors (2 -10) Calculate h, S from C(t) Diagonalize to get poles. Cheap! (Single FFT) Extends FFT to a matrix method (FFT: L=1!) Applicable to MATRIX signals Cik(t)

Developments: Mandelshtam; Taylor; Guo Shaka) • Discrete nature of signals. • Multiple time-scales. • Avoiding Diagonalization. (long time spectrum directly from short-t. )

Applications: NMR -- Multiple time-dimensions t t Semiclassical correlation functions (He-aromatic clusters; He 2 -aromatics next. ) Excited states in DMC Extracting frequencies from short-time segments – Mass spectra Classical frequencies from < v(t)v(0)>

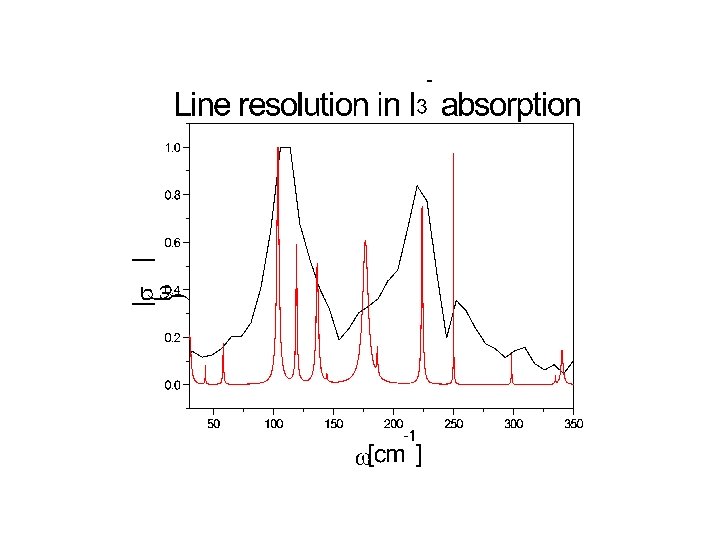
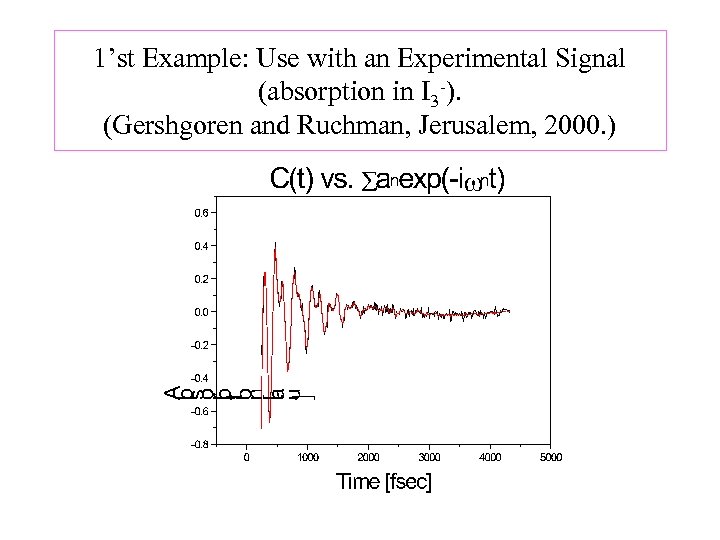1’st Example: Use with an Experimental Signal (absorption in I 3 -). (Gershgoren and Ruchman, Jerusalem, 2000. )

Matrix-correlation functions: help disentangle eigenvalues Still apply: But now:

2 nd example: Semi-classical signal with Filter-Diagonalization (Anderson, Ka, Felker, Neuhauser, 1999 -2001) • Semiclassical – excellent at short times. • Cross-correlation: helps!. • Example: He+Naphthalene (3 D system), [Developed: Trajectory-dependent Filinov]

He+Naphthalene (Earlier simulations: He+Benzene)

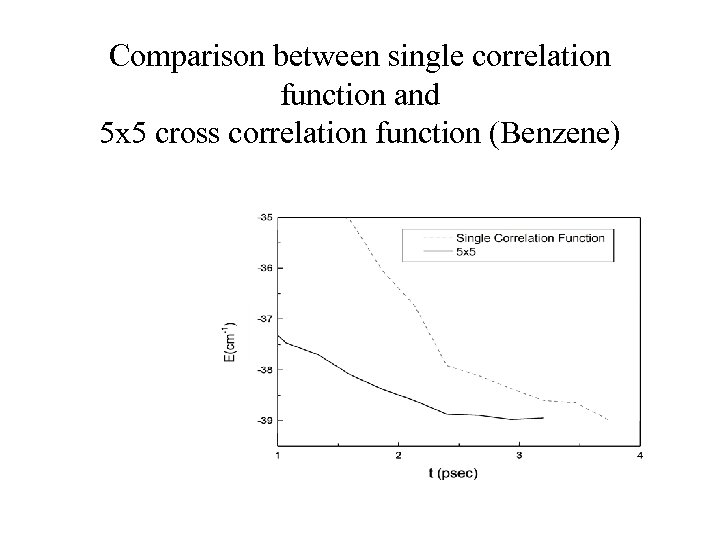Comparison between single correlation function and 5 x 5 cross correlation function (Benzene)

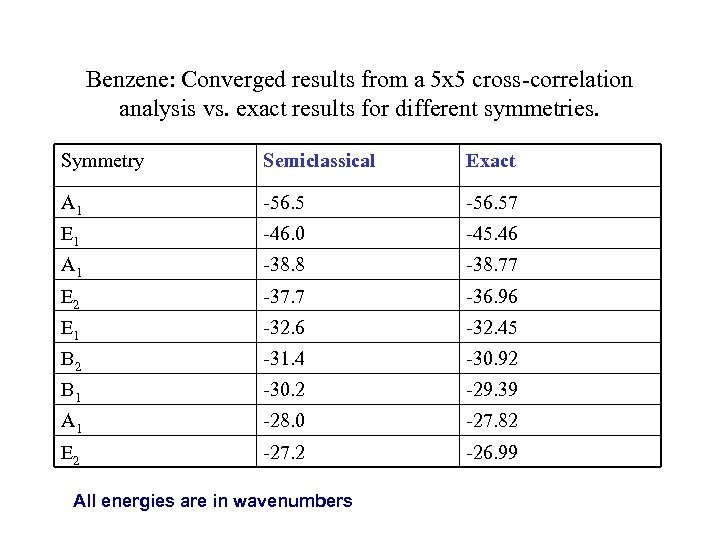Benzene: Converged results from a 5 x 5 cross-correlation analysis vs. exact results for different symmetries. Symmetry Semiclassical Exact A 1 -56. 57 E 1 -46. 0 -45. 46 A 1 -38. 8 -38. 77 E 2 -37. 7 -36. 96 E 1 -32. 6 -32. 45 B 2 -31. 4 -30. 92 B 1 -30. 2 -29. 39 A 1 -28. 0 -27. 82 E 2 -27. 2 -26. 99 All energies are in wavenumbers

Insert: Trajectory-Dependent Cellularization. Herman-Kluck Problems: (related) – Weights increasing; Trajectory chaotic – cellularization (Filinov) problematic

Filinov-Transform (Filinov, Freeman, Doll, Coalson; Manolopolous). Problem – B may be steep in certain directions Solution: make time-dependent and trajectory-dep. matrix.

Trajectory-dependent cellularization: “details” We find the 2’nd derivative matrix, set And REQUIRE And condition f so that the overall integrand is well-behaved and not large.

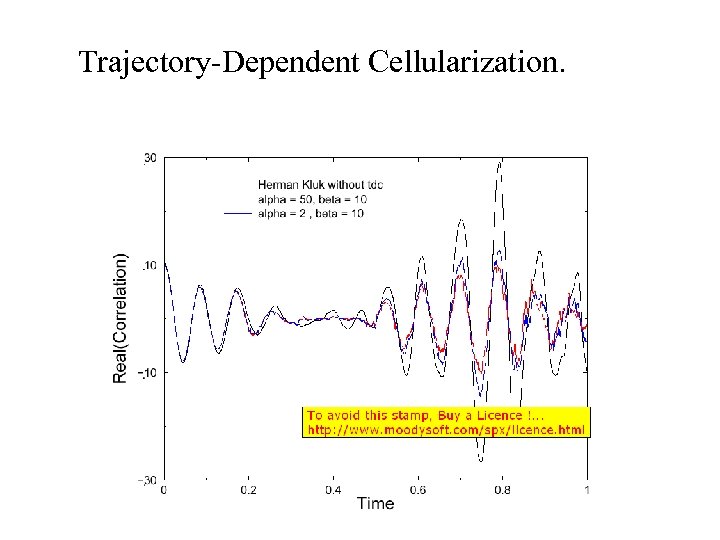Trajectory-Dependent Cellularization.

Work-in-progress : Naphthalene, Effect of Trajectory-Dependent Cellularization (single C(t), few trajectories)

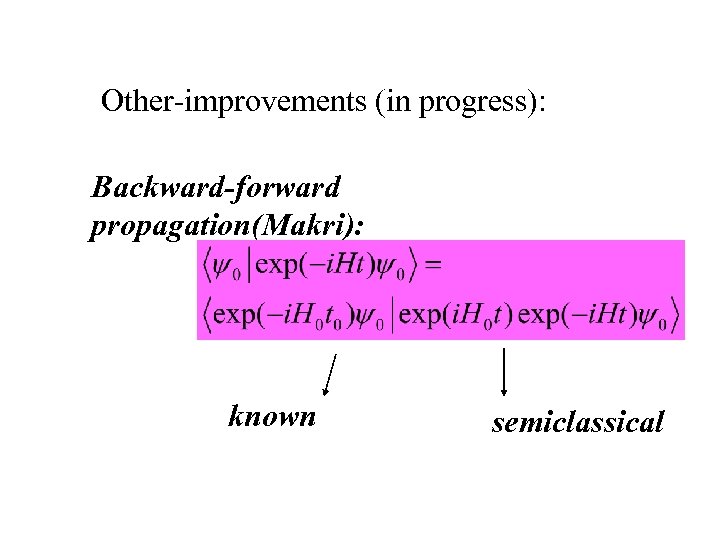Other-improvements (in progress): Backward-forward propagation(Makri): known semiclassical

3 -rd example: Eigenvalues in DMC (with Chen and Mandelshtam) (see Whaley too). Suitable for Filter-Diagonalization.

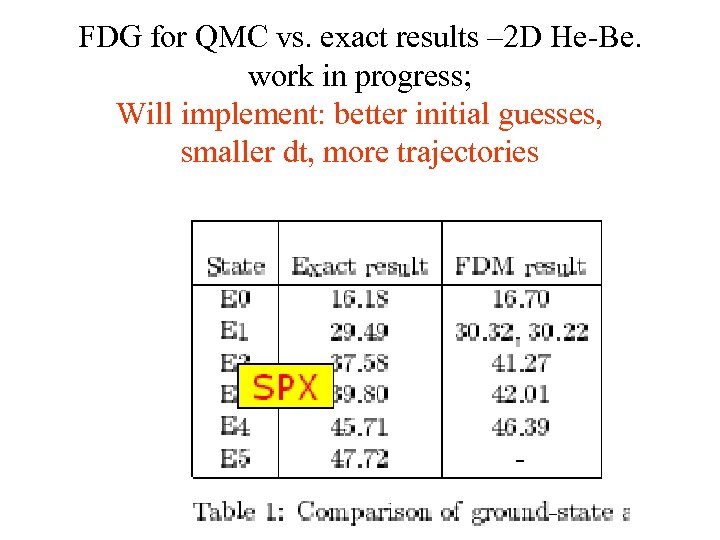FDG for QMC vs. exact results – 2 D He-Be. work in progress; Will implement: better initial guesses, smaller dt, more trajectories

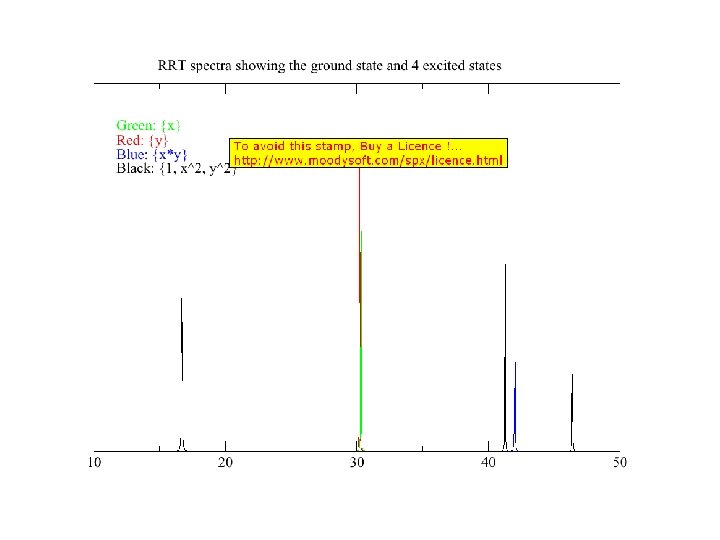
Potential for automatically many degrees of freedom (even if ground-state unknown): Ground-state If T is large.

Conclusions: Filter-Diagonalization: * Handles large signals * Applicable when long-times expensive/difficult * Is general extension of Fourier-Transforms Trajectory-dependent cellularization effective.