Fig 6 18 W H Relative sizes of cloud

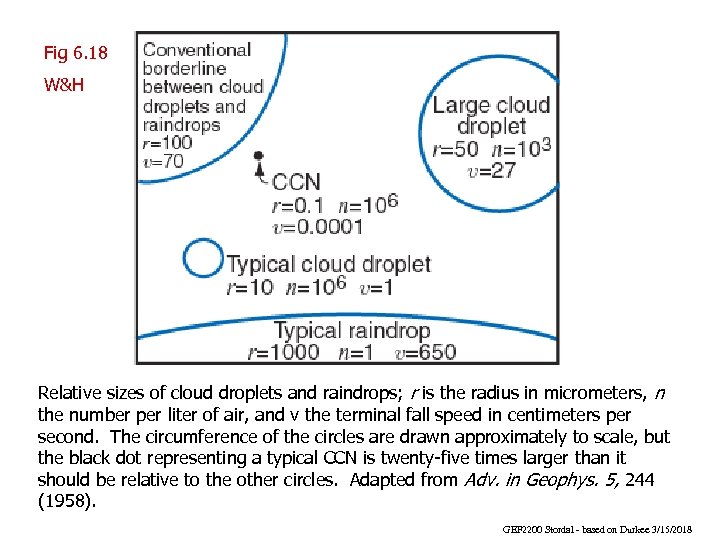Fig 6. 18 W&H Relative sizes of cloud droplets and raindrops; r is the radius in micrometers, n the number per liter of air, and v the terminal fall speed in centimeters per second. The circumference of the circles are drawn approximately to scale, but the black dot representing a typical CCN is twenty-five times larger than it should be relative to the other circles. Adapted from Adv. in Geophys. 5, 244 (1958). GEF 2200 Stordal - based on Durkee 3/15/2018

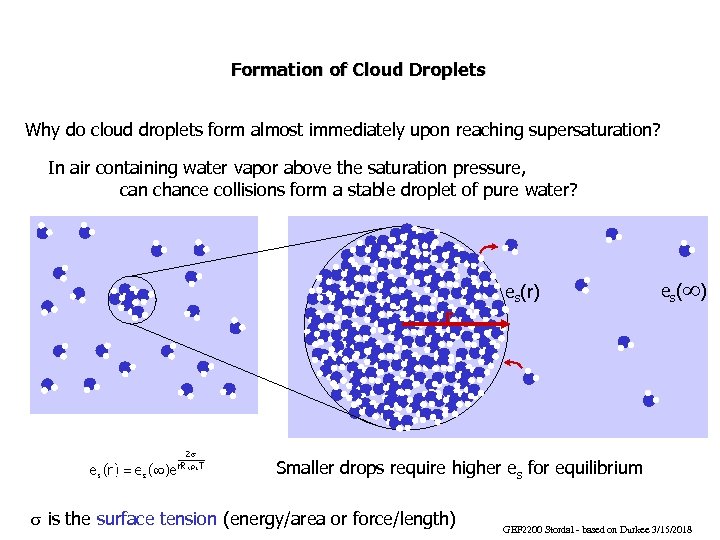Formation of Cloud Droplets Why do cloud droplets form almost immediately upon reaching supersaturation? In air containing water vapor above the saturation pressure, can chance collisions form a stable droplet of pure water? r es(r) es(¥) Smaller drops require higher es for equilibrium s is the surface tension (energy/area or force/length) GEF 2200 Stordal - based on Durkee 3/15/2018

GEF 2200 Stordal - based on Durkee 3/15/2018

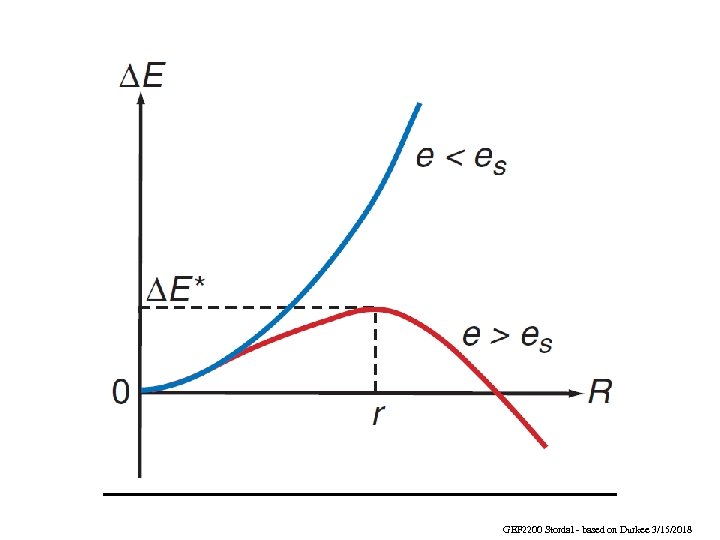
Growth depends on the difference between es(r) and e e < es(r) e > es(r) decay (vapor moves away from the drop) growth (vapor moves toward the drop) When the radius is such that e = es(r) the droplet is just large enough to be stable: where S = e/es(¥) is the saturation ratio (Eq. 6. 5 W&H) Statistical thermodynamic calculations show that S must be 300 -600% for one homogeneous nucleation event per cm 3 per second in the natural atmosphere. Since S rarely exceeds 1 -2%, homogeneous nucleation is never consistently achieved. GEF 2200 Stordal - based on Durkee 3/15/2018

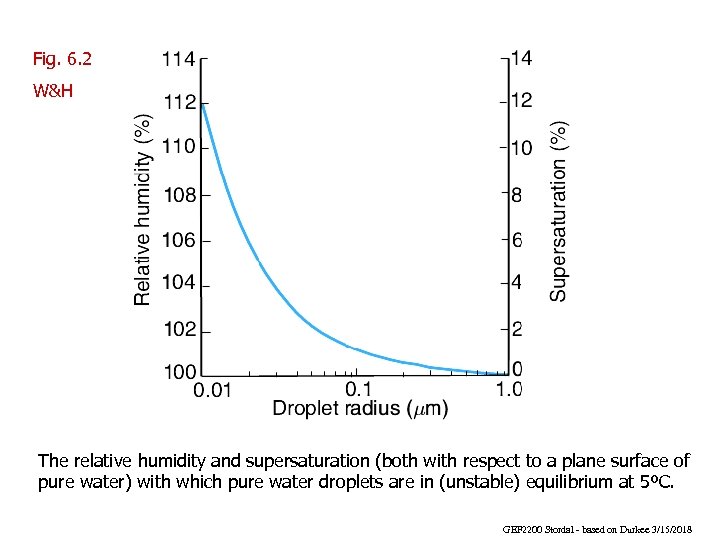Fig. 6. 2 W&H The relative humidity and supersaturation (both with respect to a plane surface of pure water) with which pure water droplets are in (unstable) equilibrium at 5ºC. GEF 2200 Stordal - based on Durkee 3/15/2018

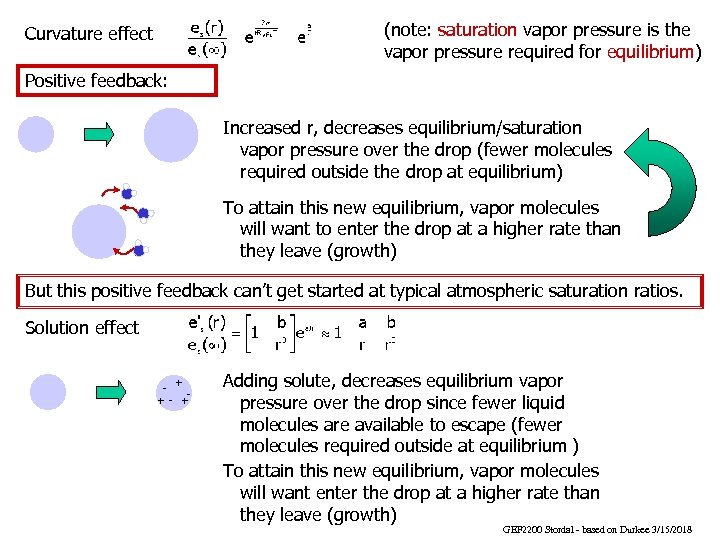(note: saturation vapor pressure is the vapor pressure required for equilibrium) Curvature effect Positive feedback: Increased r, decreases equilibrium/saturation vapor pressure over the drop (fewer molecules required outside the drop at equilibrium) To attain this new equilibrium, vapor molecules will want to enter the drop at a higher rate than they leave (growth) But this positive feedback can’t get started at typical atmospheric saturation ratios. Solution effect + + - + Adding solute, decreases equilibrium vapor pressure over the drop since fewer liquid molecules are available to escape (fewer molecules required outside at equilibrium ) To attain this new equilibrium, vapor molecules will want enter the drop at a higher rate than they leave (growth) GEF 2200 Stordal - based on Durkee 3/15/2018

Nucleation of droplets requires a particle (condensation nucleus). Hygroscopic nuclei are soluble in water and decrease es(r) significantly. hygroscopic - + + - ++ + - hydrophobic - + r- - + + + - es(r) + - With non-water molecules on the surface, the equilibrium (equal transfer across the interface) occurs at lower pressure ~Eq. 6. 6 W&H M = mass of solute C = 3 imv/4 pr. Lms GEF 2200 Stordal - based on Durkee 3/15/2018

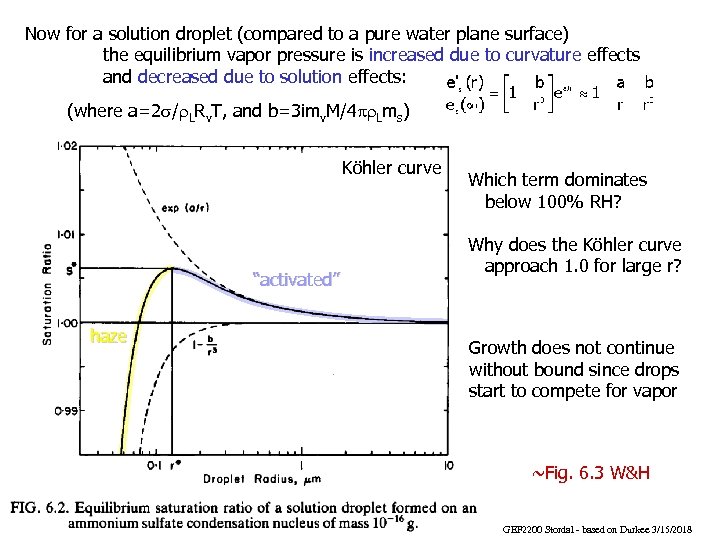Now for a solution droplet (compared to a pure water plane surface) the equilibrium vapor pressure is increased due to curvature effects and decreased due to solution effects: (where a=2 s/r. LRv. T, and b=3 imv. M/4 pr. Lms) Köhler curve “activated” haze Which term dominates below 100% RH? Why does the Köhler curve approach 1. 0 for large r? Growth does not continue without bound since drops start to compete for vapor ~Fig. 6. 3 W&H GEF 2200 Stordal - based on Durkee 3/15/2018

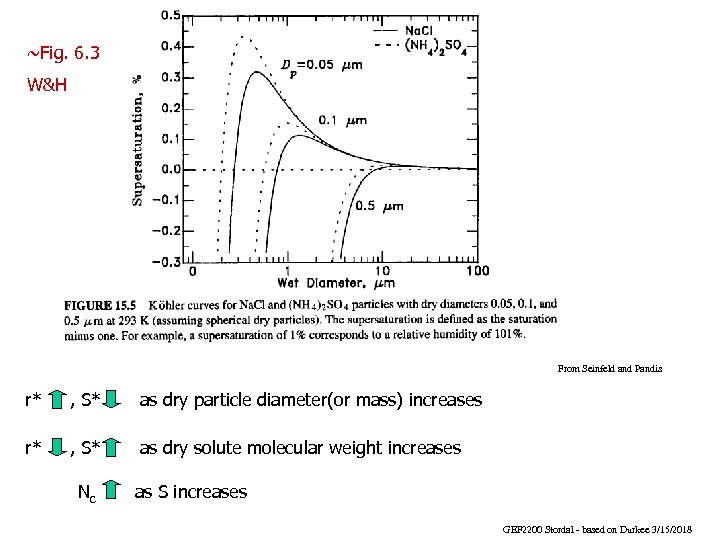~Fig. 6. 3 W&H From Seinfeld and Pandis r* , S* as dry particle diameter(or mass) increases r* , S* as dry solute molecular weight increases Nc as S increases GEF 2200 Stordal - based on Durkee 3/15/2018

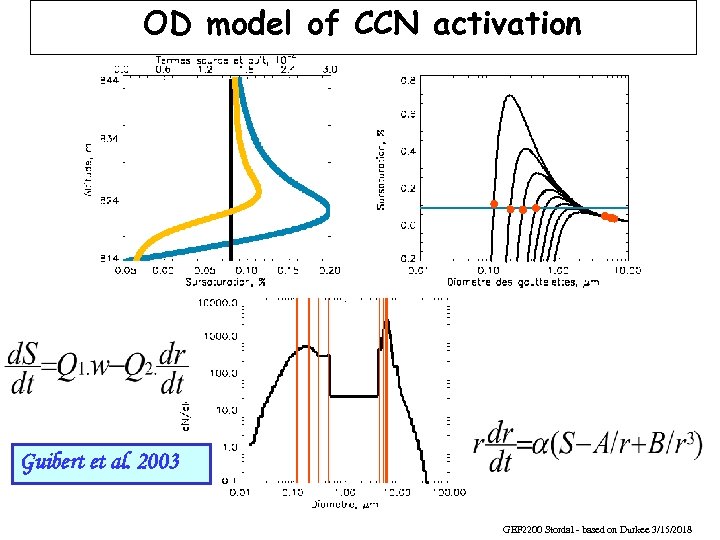OD model of CCN activation S = Smax Guibert et al. 2003 GEF 2200 Stordal - based on Durkee 3/15/2018

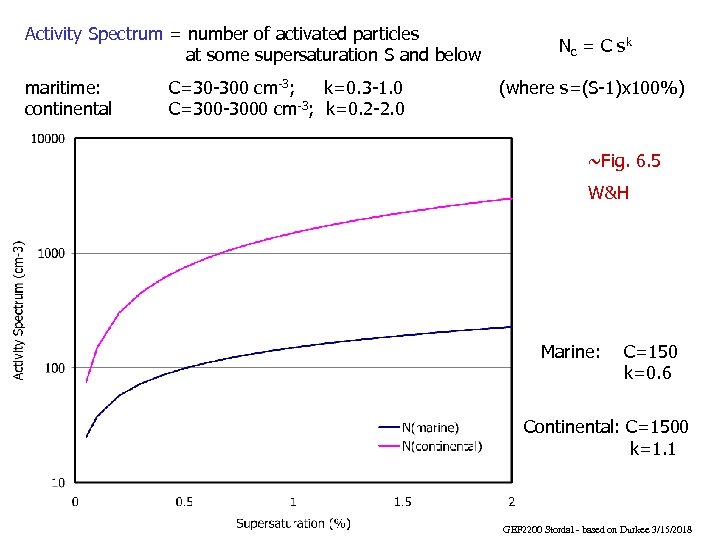Activity Spectrum = number of activated particles at some supersaturation S and below maritime: continental C=30 -300 cm-3; k=0. 3 -1. 0 C=300 -3000 cm-3; k=0. 2 -2. 0 Nc = C s k (where s=(S-1)x 100%) ~Fig. 6. 5 W&H Marine: C=150 k=0. 6 Continental: C=1500 k=1. 1 GEF 2200 Stordal - based on Durkee 3/15/2018

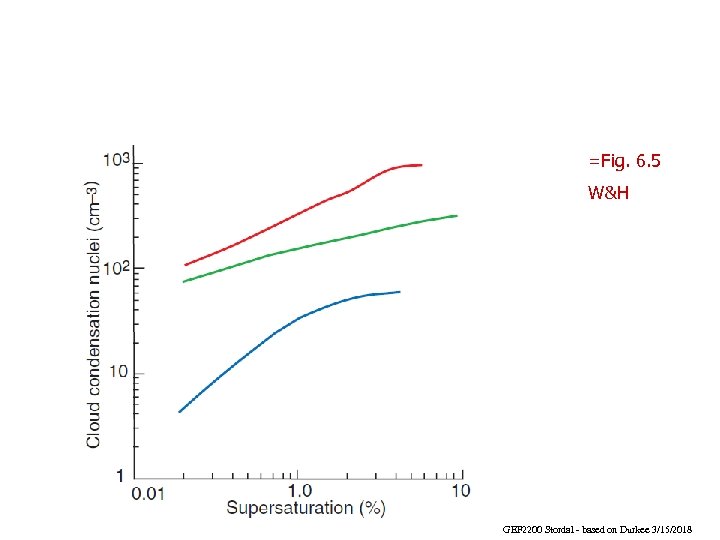=Fig. 6. 5 W&H GEF 2200 Stordal - based on Durkee 3/15/2018

Supersaturation is controlled by updraft velocity so. . . Marine: C=150 k=0. 6 Continental: C=1500 k=1. 1 GEF 2200 Stordal - based on Durkee 3/15/2018

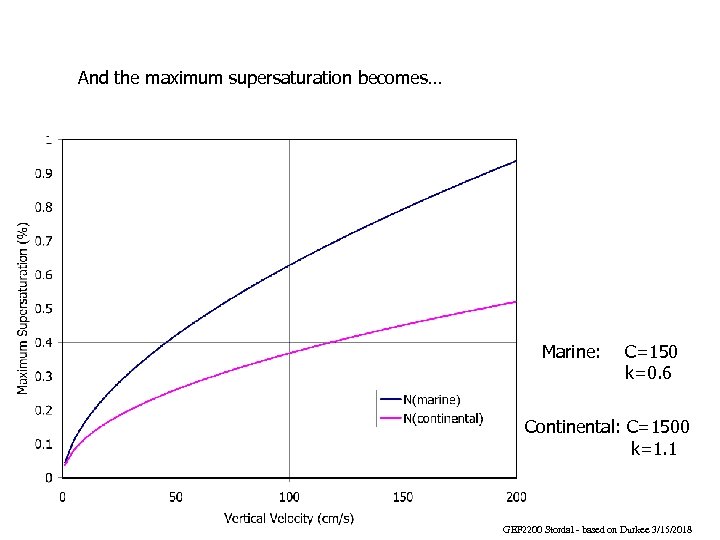And the maximum supersaturation becomes… Marine: C=150 k=0. 6 Continental: C=1500 k=1. 1 GEF 2200 Stordal - based on Durkee 3/15/2018

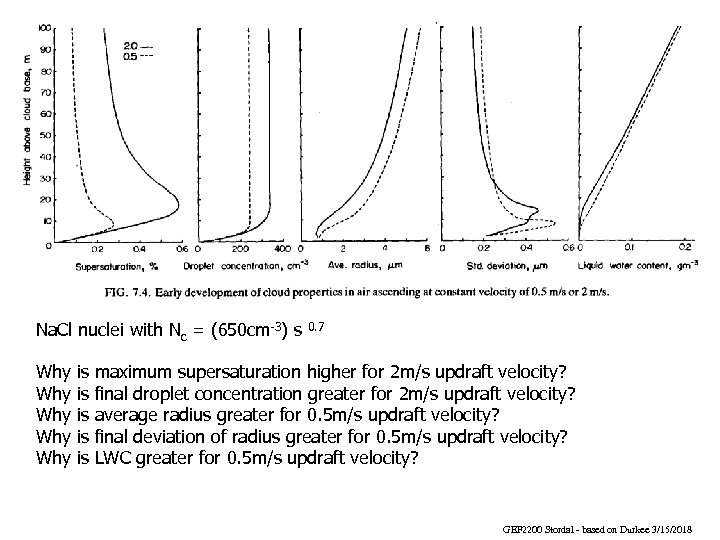Na. Cl nuclei with Nc = (650 cm-3) s Why Why Why is is is 0. 7 maximum supersaturation higher for 2 m/s updraft velocity? final droplet concentration greater for 2 m/s updraft velocity? average radius greater for 0. 5 m/s updraft velocity? final deviation of radius greater for 0. 5 m/s updraft velocity? LWC greater for 0. 5 m/s updraft velocity? GEF 2200 Stordal - based on Durkee 3/15/2018

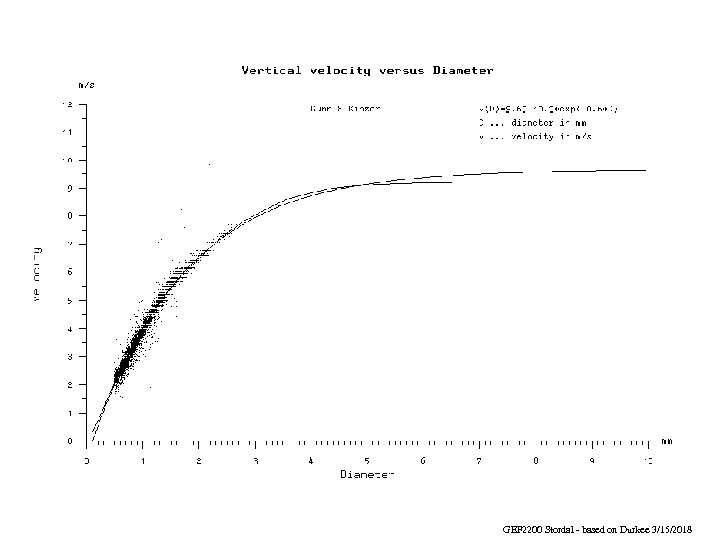GEF 2200 Stordal - based on Durkee 3/15/2018

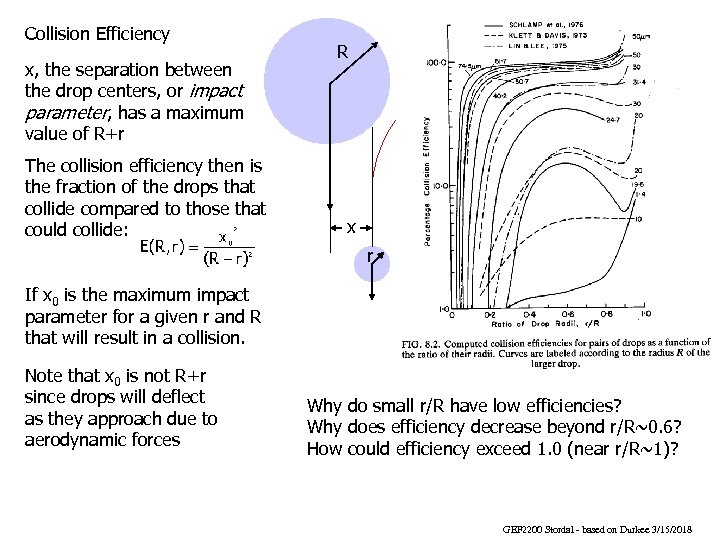Collision Efficiency x, the separation between the drop centers, or impact parameter, has a maximum value of R+r The collision efficiency then is the fraction of the drops that collide compared to those that could collide: R x r If x 0 is the maximum impact parameter for a given r and R that will result in a collision. Note that x 0 is not R+r since drops will deflect as they approach due to aerodynamic forces Why do small r/R have low efficiencies? Why does efficiency decrease beyond r/R~0. 6? How could efficiency exceed 1. 0 (near r/R~1)? GEF 2200 Stordal - based on Durkee 3/15/2018

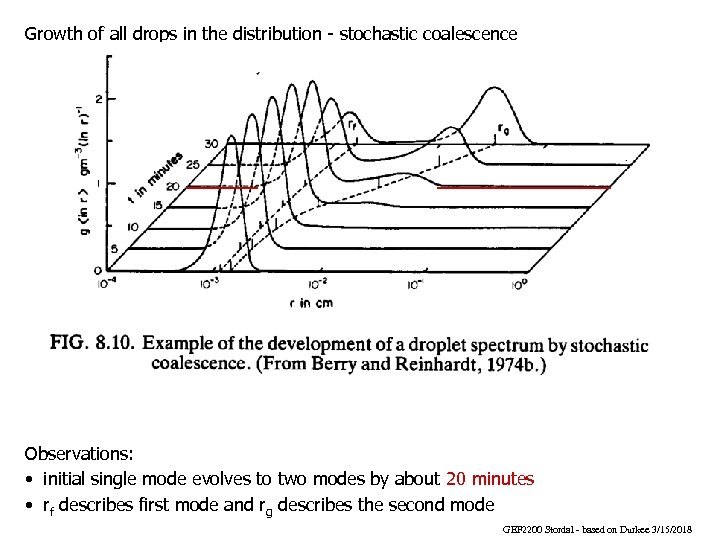Growth of all drops in the distribution - stochastic coalescence Observations: • initial single mode evolves to two modes by about 20 minutes • rf describes first mode and rg describes the second mode GEF 2200 Stordal - based on Durkee 3/15/2018