lectures both.ppt
- Количество слайдов: 147
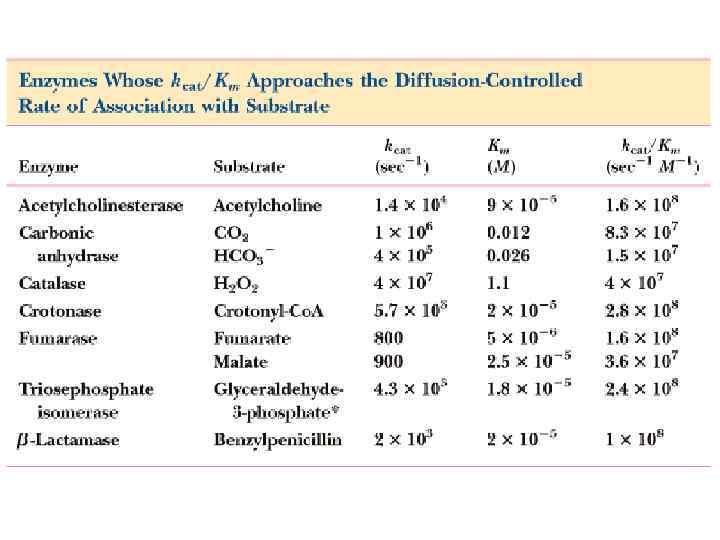
 ФЕРМЕНТАТИВНАЯ КИНЕТИКА
ФЕРМЕНТАТИВНАЯ КИНЕТИКА
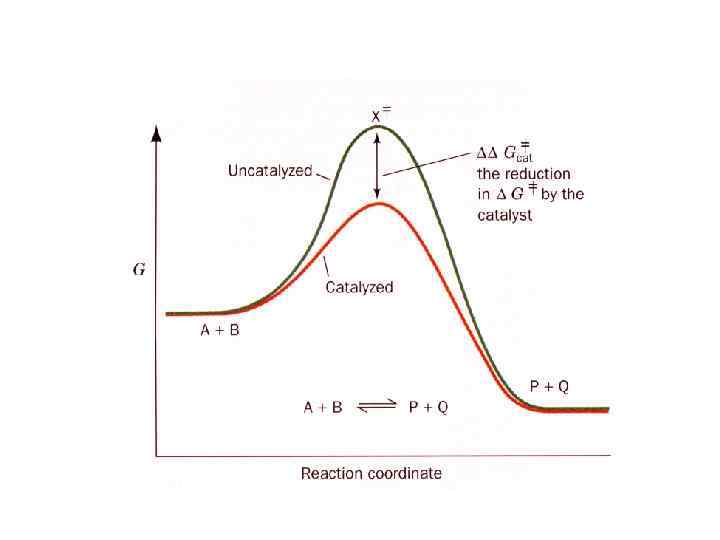
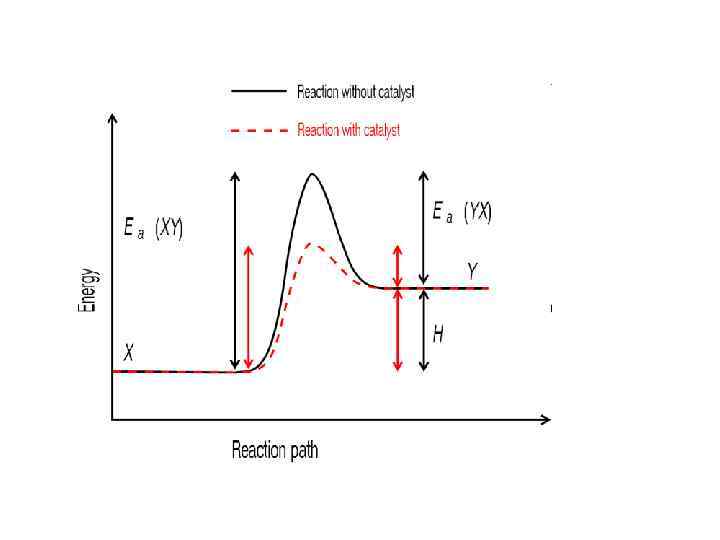
 Ферменты – чрезвычайно эффективные катализаторы
Ферменты – чрезвычайно эффективные катализаторы
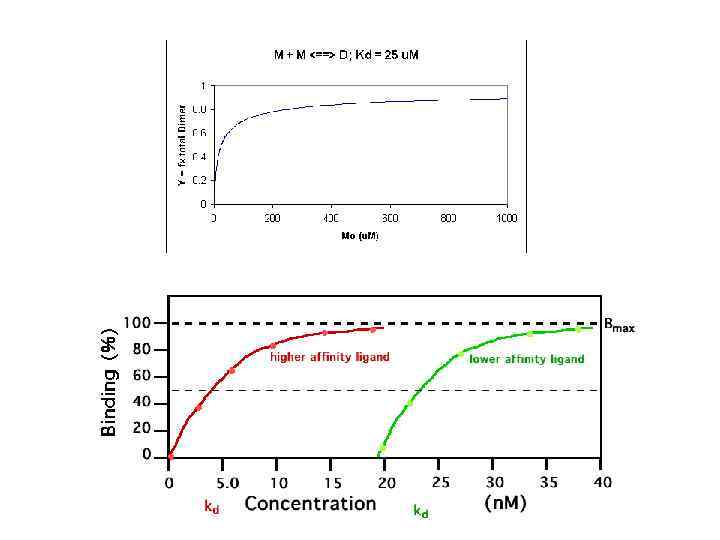
![[ML] = [M 0][L]/(KD+ [L] Y = fractional saturation = ([ML]/[M 0] = [L]/(KD+ [ML] = [M 0][L]/(KD+ [L] Y = fractional saturation = ([ML]/[M 0] = [L]/(KD+](https://present5.com/presentation/3540715_33786667/image-6.jpg) [ML] = [M 0][L]/(KD+ [L] Y = fractional saturation = ([ML]/[M 0] = [L]/(KD+ [L]) K d = ([M][L])/[ML] = [Mo-ML][L])/[ML]
[ML] = [M 0][L]/(KD+ [L] Y = fractional saturation = ([ML]/[M 0] = [L]/(KD+ [L]) K d = ([M][L])/[ML] = [Mo-ML][L])/[ML]
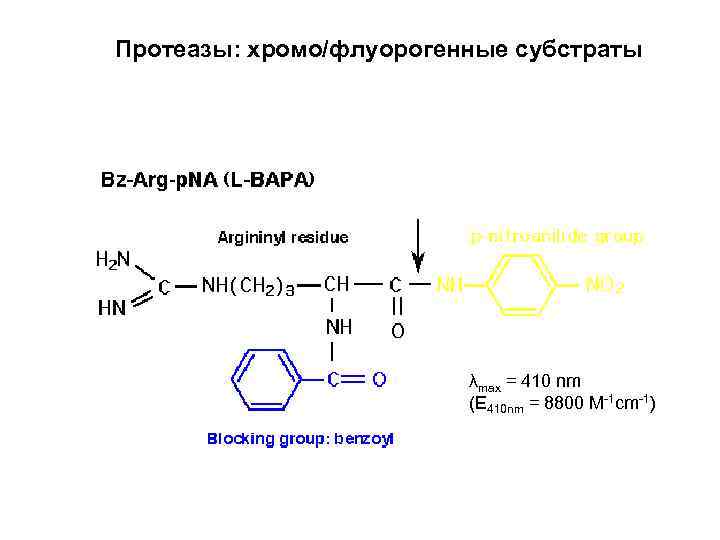 Протеазы: хромо/флуорогенные субстраты λmax = 410 nm (E 410 nm = 8800 M-1 cm-1)
Протеазы: хромо/флуорогенные субстраты λmax = 410 nm (E 410 nm = 8800 M-1 cm-1)
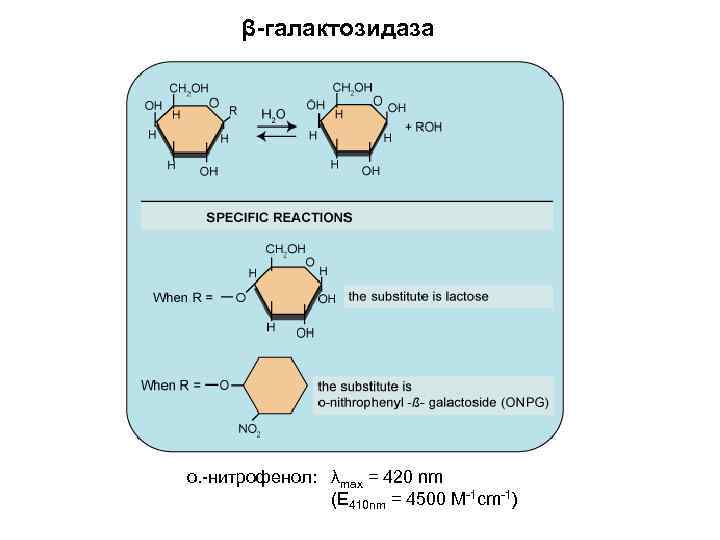 β-галактозидаза о. -нитрофенол: λmax = 420 nm (E 410 nm = 4500 M-1 cm-1)
β-галактозидаза о. -нитрофенол: λmax = 420 nm (E 410 nm = 4500 M-1 cm-1)
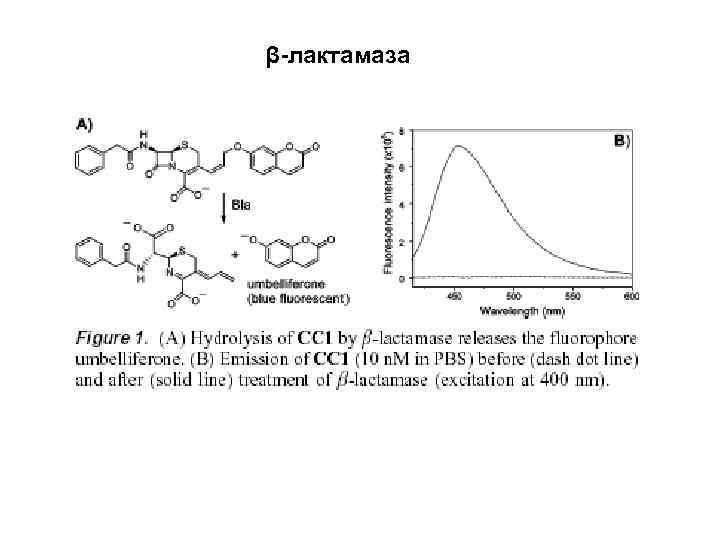 β-лактамаза
β-лактамаза
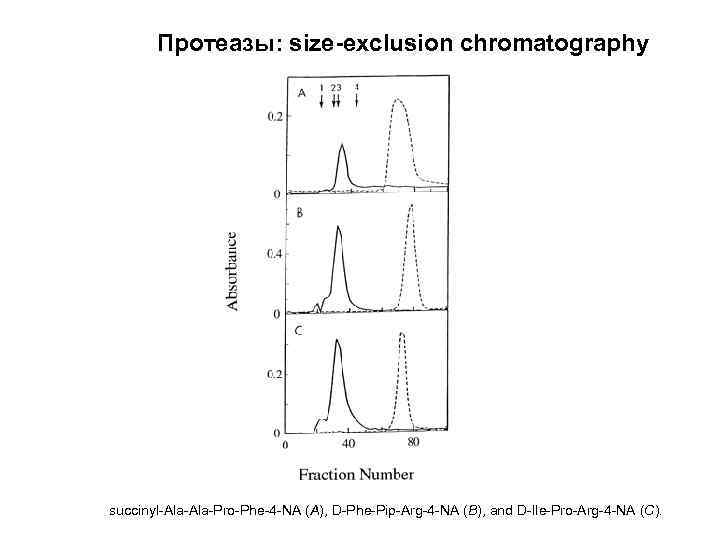 Протеазы: size-exclusion chromatography succinyl-Ala-Pro-Phe-4 -NA (A), D-Phe-Pip-Arg-4 -NA (B), and D-Ile-Pro-Arg-4 -NA (C).
Протеазы: size-exclusion chromatography succinyl-Ala-Pro-Phe-4 -NA (A), D-Phe-Pip-Arg-4 -NA (B), and D-Ile-Pro-Arg-4 -NA (C).
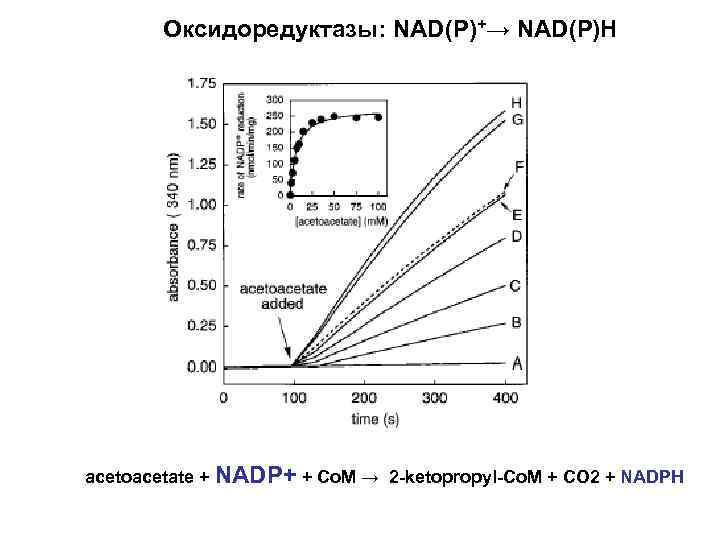 Оксидоредуктазы: NAD(P)+→ NAD(P)H acetoacetate + NADP+ + Co. M → 2 -ketopropyl-Co. M + CO 2 + NADPH
Оксидоредуктазы: NAD(P)+→ NAD(P)H acetoacetate + NADP+ + Co. M → 2 -ketopropyl-Co. M + CO 2 + NADPH
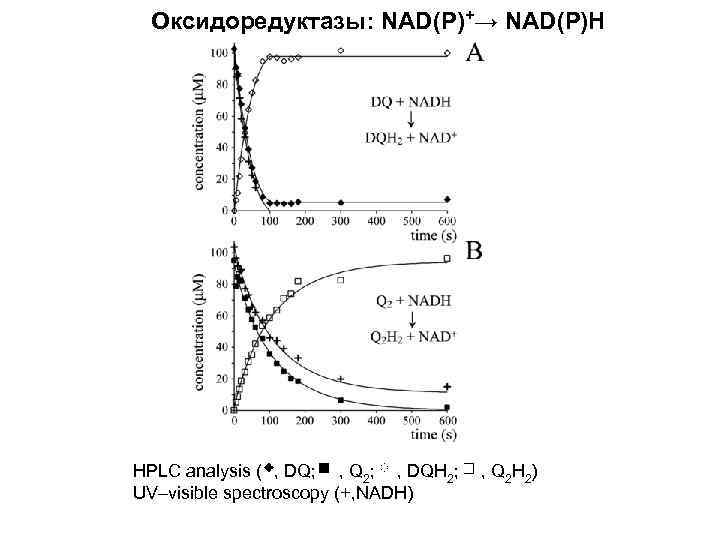 Оксидоредуктазы: NAD(P)+→ NAD(P)H HPLC analysis ( , DQ; , Q 2; , DQH 2; , Q 2 H 2) UV–visible spectroscopy (+, NADH)
Оксидоредуктазы: NAD(P)+→ NAD(P)H HPLC analysis ( , DQ; , Q 2; , DQH 2; , Q 2 H 2) UV–visible spectroscopy (+, NADH)
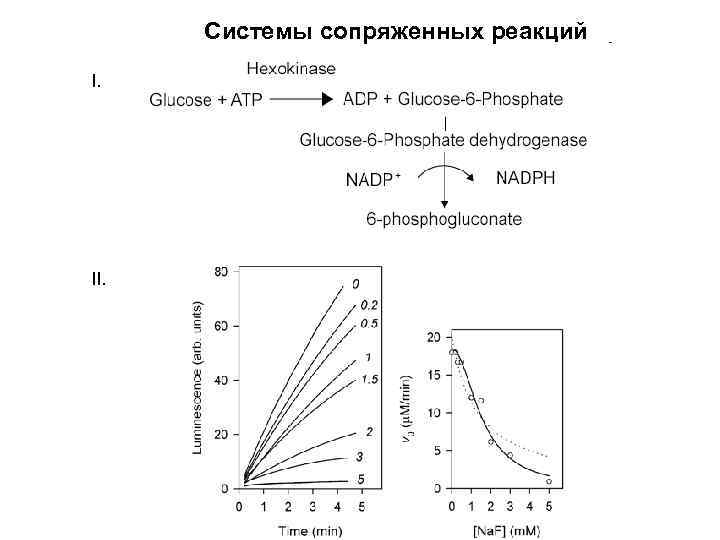 Cистемы сопряженных реакций I. II.
Cистемы сопряженных реакций I. II.
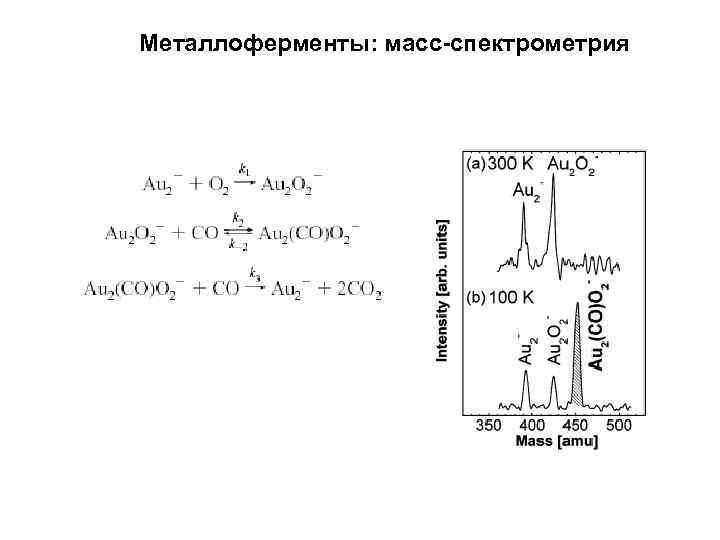 Металлоферменты: масс-спектрометрия
Металлоферменты: масс-спектрометрия
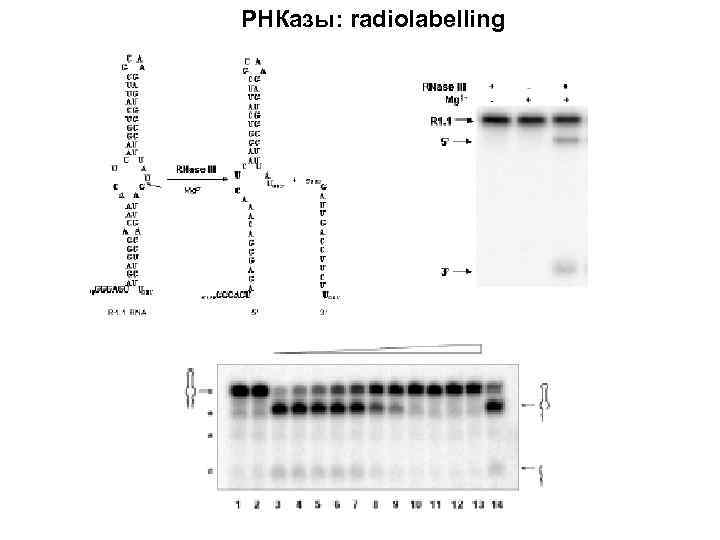 РНКазы: radiolabelling
РНКазы: radiolabelling
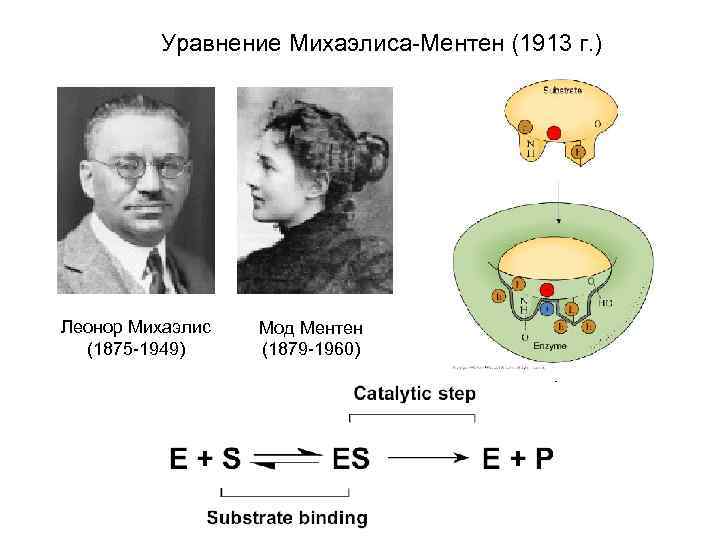 Уравнение Михаэлиса-Ментен (1913 г. ) Леонор Михаэлис (1875 -1949) Мод Ментен (1879 -1960)
Уравнение Михаэлиса-Ментен (1913 г. ) Леонор Михаэлис (1875 -1949) Мод Ментен (1879 -1960)
 Уравнение Михаэлиса-Ментен Первоначальная схема Михаэлиса предусматривает: 1. Обязательное образование фермент-субстратного комплекса ( «комплекс Михаэлиса» ) 2. k 2<
Уравнение Михаэлиса-Ментен Первоначальная схема Михаэлиса предусматривает: 1. Обязательное образование фермент-субстратного комплекса ( «комплекс Михаэлиса» ) 2. k 2<
 Уравнение Михаэлиса-Ментен
Уравнение Михаэлиса-Ментен
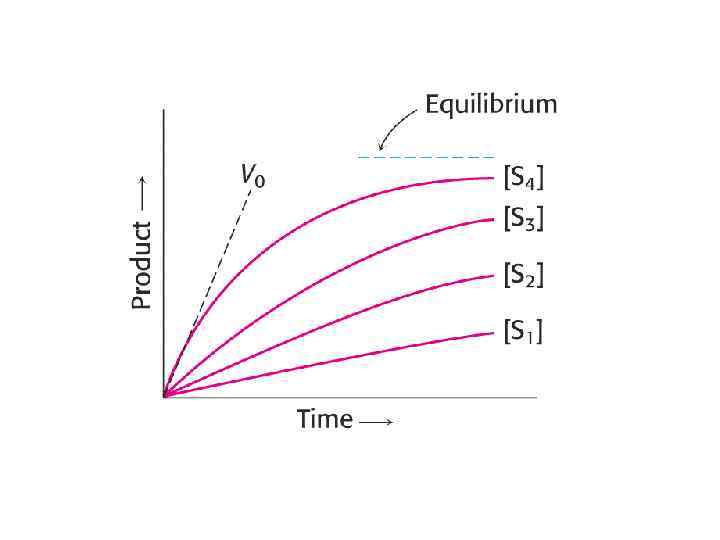
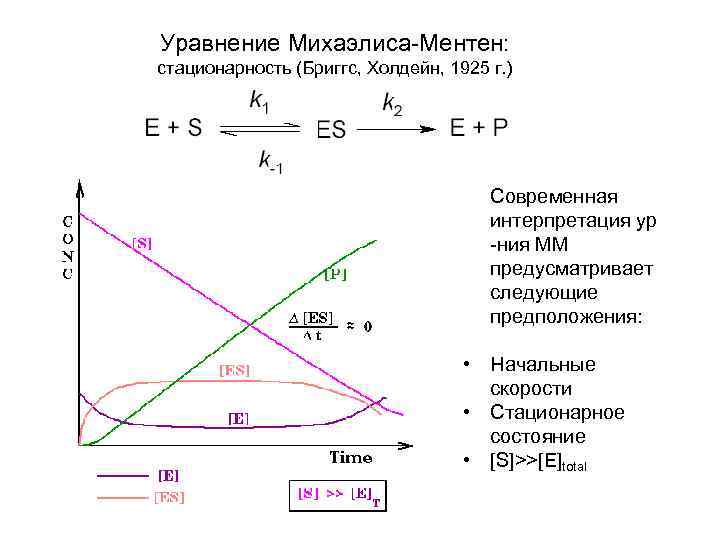 Уравнение Михаэлиса-Ментен: стационарность (Бриггс, Холдейн, 1925 г. ) Современная интерпретация ур -ния ММ предусматривает следующие предположения: • Начальные скорости • Стационарное состояние • [S]>>[E]total
Уравнение Михаэлиса-Ментен: стационарность (Бриггс, Холдейн, 1925 г. ) Современная интерпретация ур -ния ММ предусматривает следующие предположения: • Начальные скорости • Стационарное состояние • [S]>>[E]total
 Уравнение Михаэлиса-Ментен: стационарность Скорость катализируемой реакции Скорость образования ES Скорость распада ES
Уравнение Михаэлиса-Ментен: стационарность Скорость катализируемой реакции Скорость образования ES Скорость распада ES
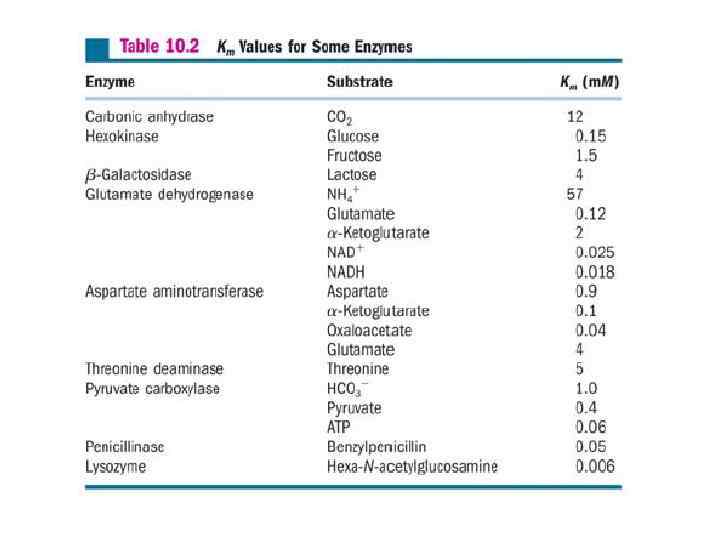
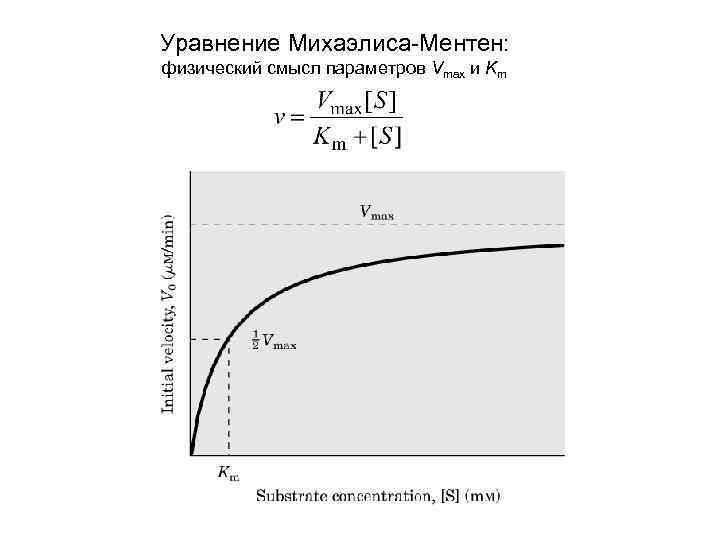 Уравнение Михаэлиса-Ментен: физический смысл параметров Vmax и Km
Уравнение Михаэлиса-Ментен: физический смысл параметров Vmax и Km
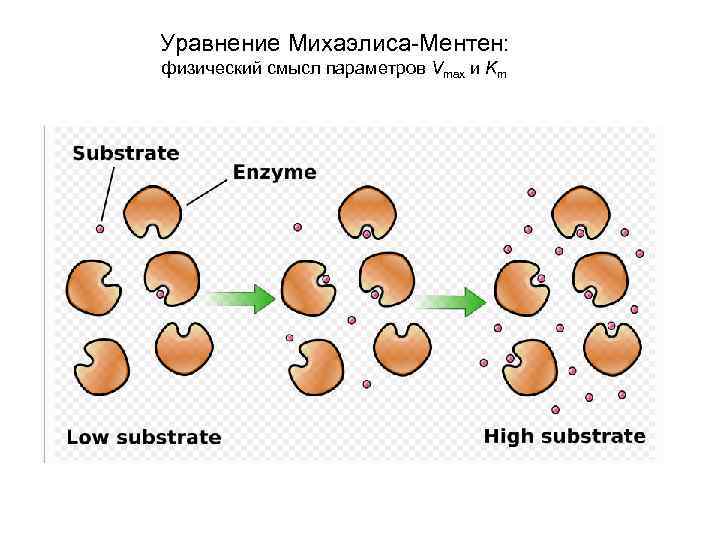 Уравнение Михаэлиса-Ментен: физический смысл параметров Vmax и Km
Уравнение Михаэлиса-Ментен: физический смысл параметров Vmax и Km
![Уравнение Михаэлиса-Ментен: физический смысл параметров Vmax и Km Vmax = kcat [E]total Уравнение Михаэлиса-Ментен: физический смысл параметров Vmax и Km Vmax = kcat [E]total](https://present5.com/presentation/3540715_33786667/image-27.jpg) Уравнение Михаэлиса-Ментен: физический смысл параметров Vmax и Km Vmax = kcat [E]total
Уравнение Михаэлиса-Ментен: физический смысл параметров Vmax и Km Vmax = kcat [E]total
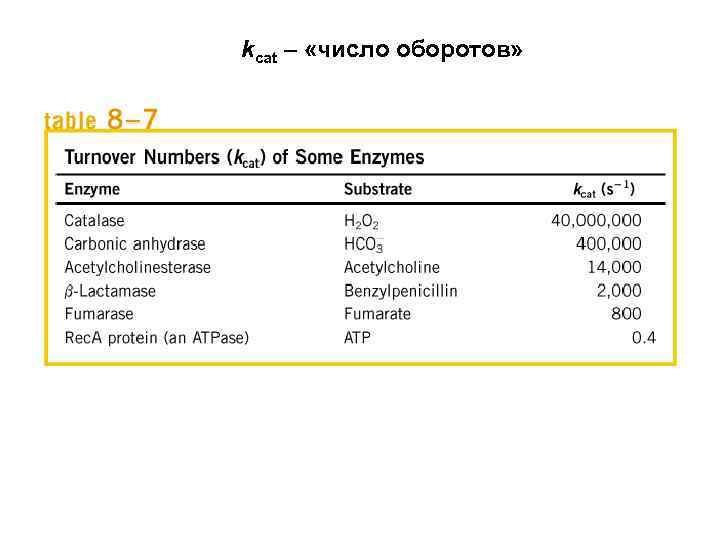 kcat – «число оборотов»
kcat – «число оборотов»
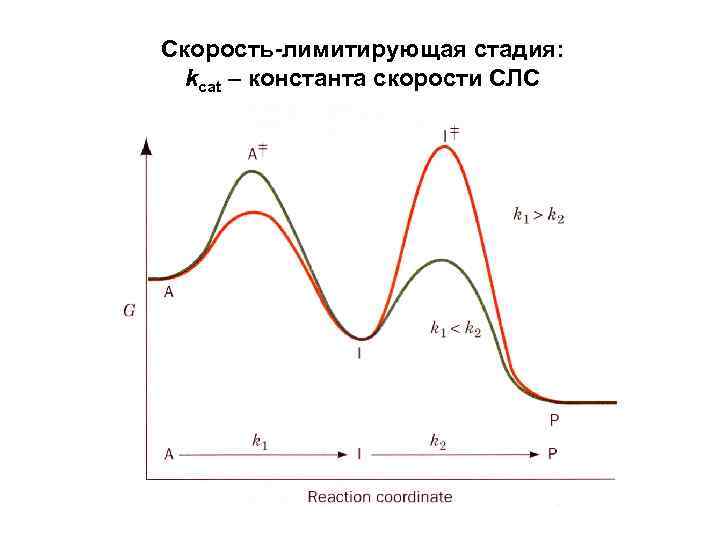 Скорость-лимитирующая стадия: kcat – константа скорости СЛС
Скорость-лимитирующая стадия: kcat – константа скорости СЛС
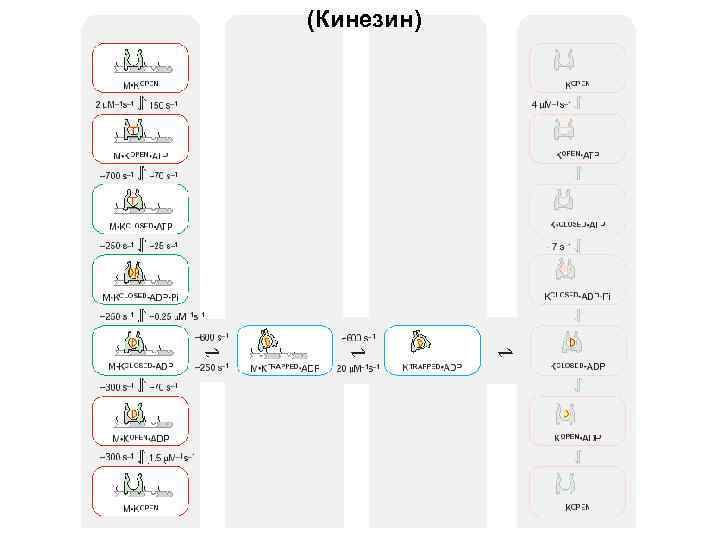 (Кинезин)
(Кинезин)

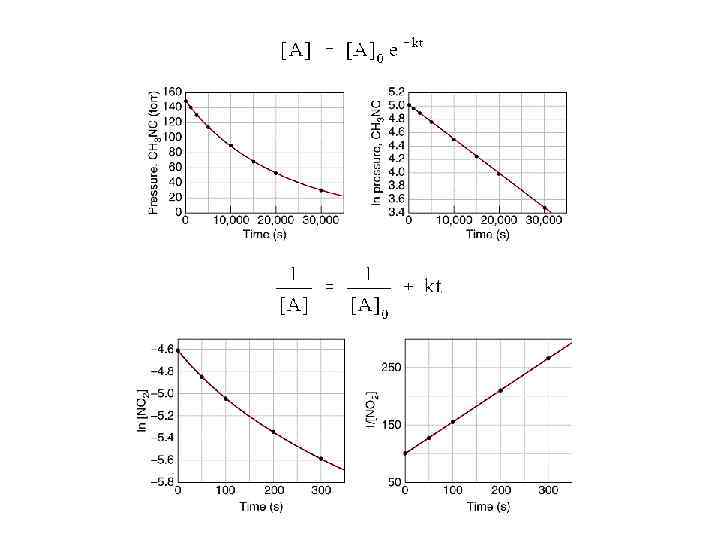
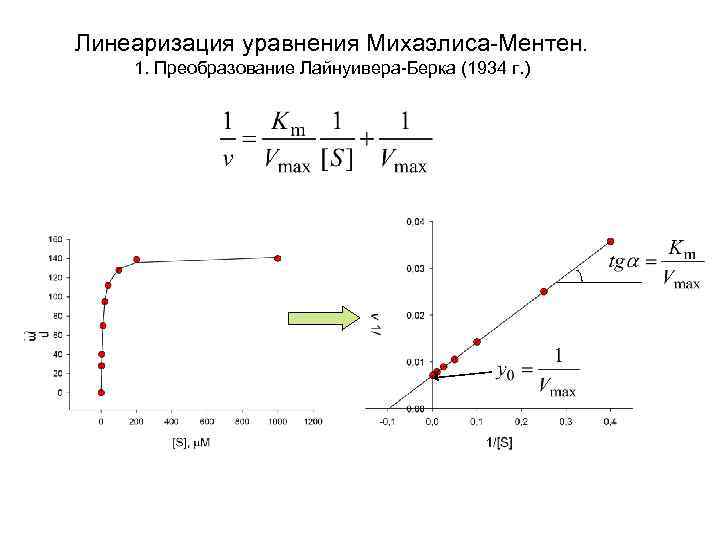 Линеаризация уравнения Михаэлиса-Ментен. 1. Преобразование Лайнуивера-Берка (1934 г. )
Линеаризация уравнения Михаэлиса-Ментен. 1. Преобразование Лайнуивера-Берка (1934 г. )
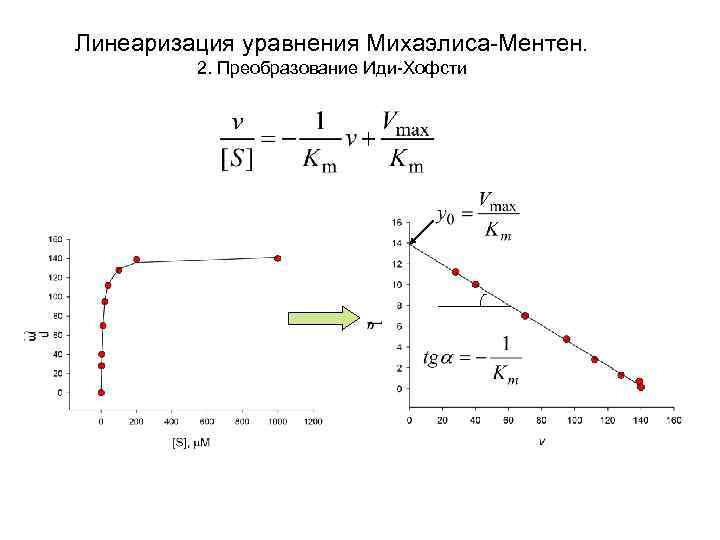 Линеаризация уравнения Михаэлиса-Ментен. 2. Преобразование Иди-Хофсти
Линеаризация уравнения Михаэлиса-Ментен. 2. Преобразование Иди-Хофсти
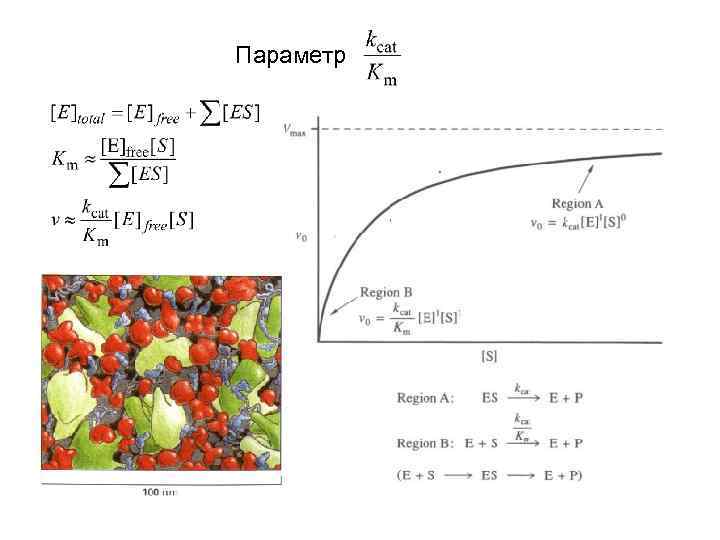 Параметр
Параметр
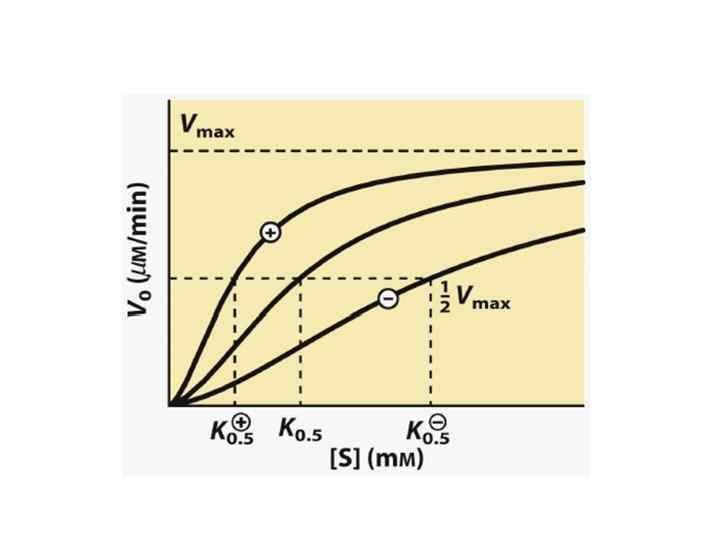
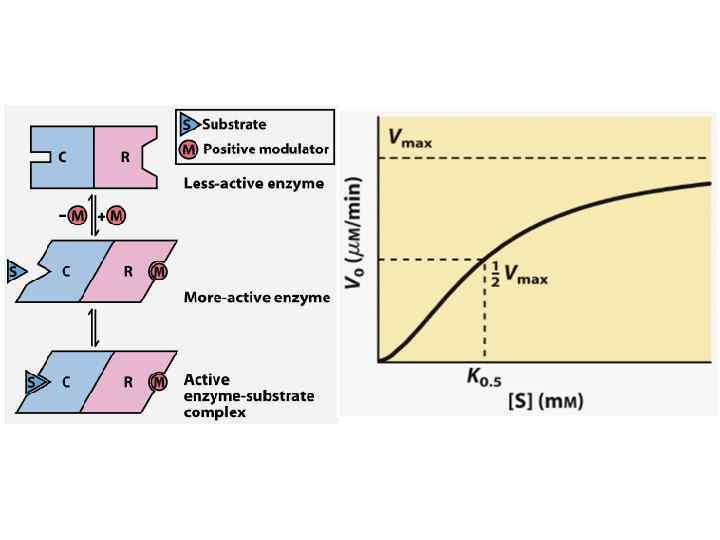
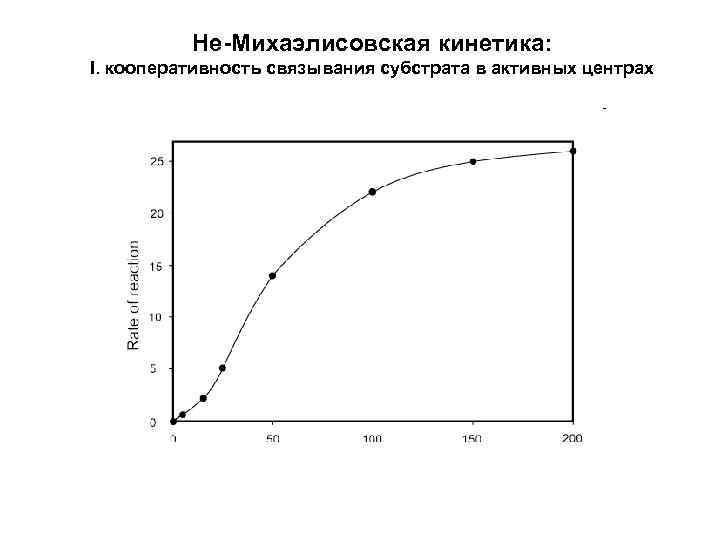 Не-Михаэлисовская кинетика: I. кооперативность связывания субстрата в активных центрах
Не-Михаэлисовская кинетика: I. кооперативность связывания субстрата в активных центрах
 Не-Михаэлисовская кинетика: I. кооперативность связывания субстрата в активных центрах h = Hill coefficient
Не-Михаэлисовская кинетика: I. кооперативность связывания субстрата в активных центрах h = Hill coefficient
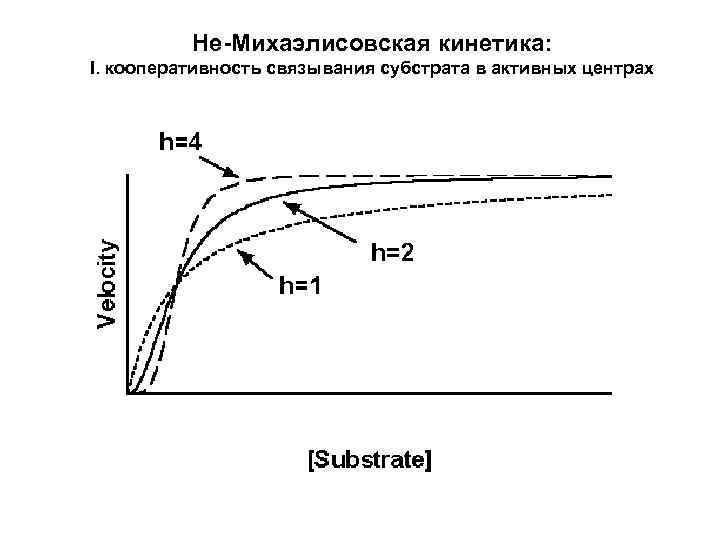 Не-Михаэлисовская кинетика: I. кооперативность связывания субстрата в активных центрах
Не-Михаэлисовская кинетика: I. кооперативность связывания субстрата в активных центрах
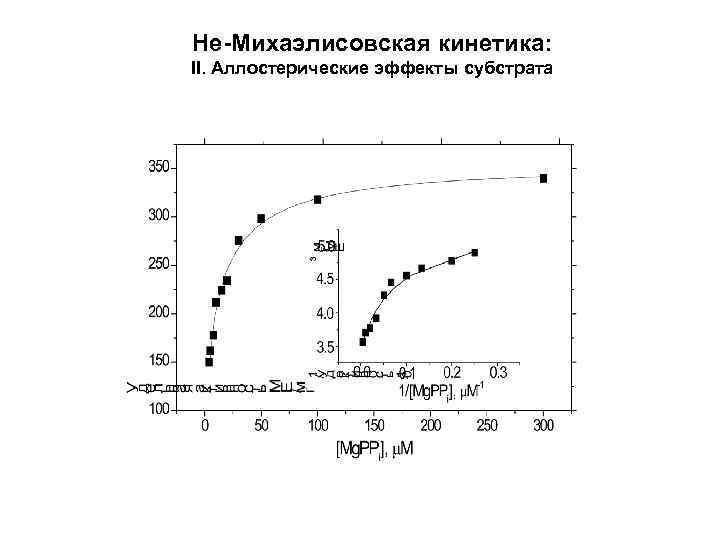 Не-Михаэлисовская кинетика: II. Аллостерические эффекты субстрата
Не-Михаэлисовская кинетика: II. Аллостерические эффекты субстрата
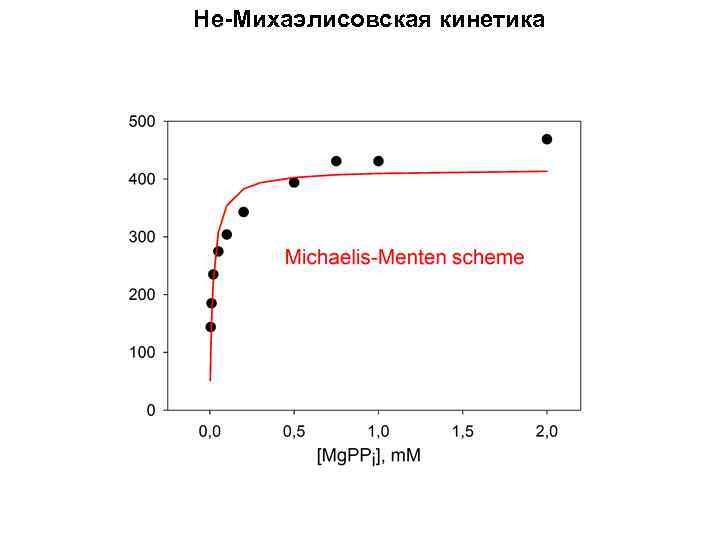 Не-Михаэлисовская кинетика
Не-Михаэлисовская кинетика
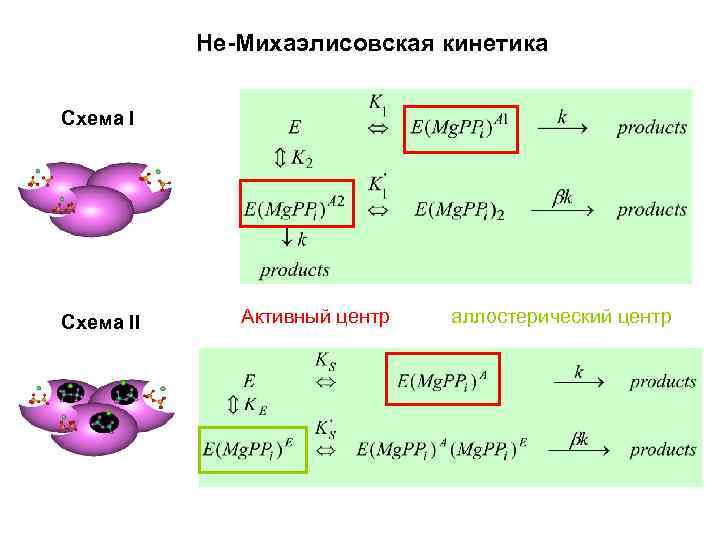 Не-Михаэлисовская кинетика Схема II Активный центр аллостерический центр
Не-Михаэлисовская кинетика Схема II Активный центр аллостерический центр
 Не-Михаэлисовская кинетика Polynomial Scheme I coefficient Scheme III 1 A Scheme II 1 KS KS B C D E K 1
Не-Михаэлисовская кинетика Polynomial Scheme I coefficient Scheme III 1 A Scheme II 1 KS KS B C D E K 1
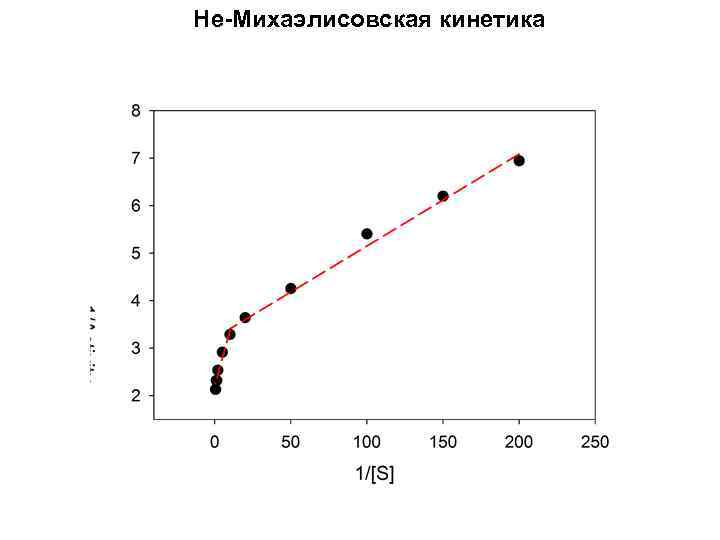 Не-Михаэлисовская кинетика
Не-Михаэлисовская кинетика
 Не-Михаэлисовская кинетика Parameter Scheme III Low substrate concentrations slope a 1 Y-intercept b 1 High substrate concentration slope a 2 Y-intercept b 2
Не-Михаэлисовская кинетика Parameter Scheme III Low substrate concentrations slope a 1 Y-intercept b 1 High substrate concentration slope a 2 Y-intercept b 2
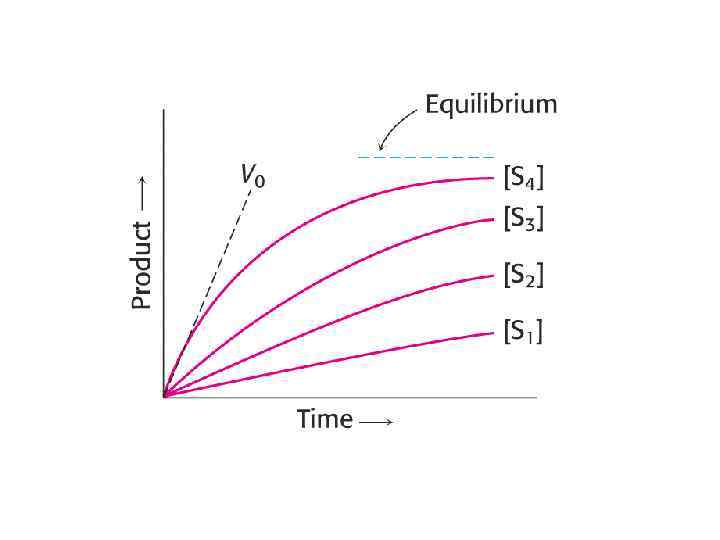
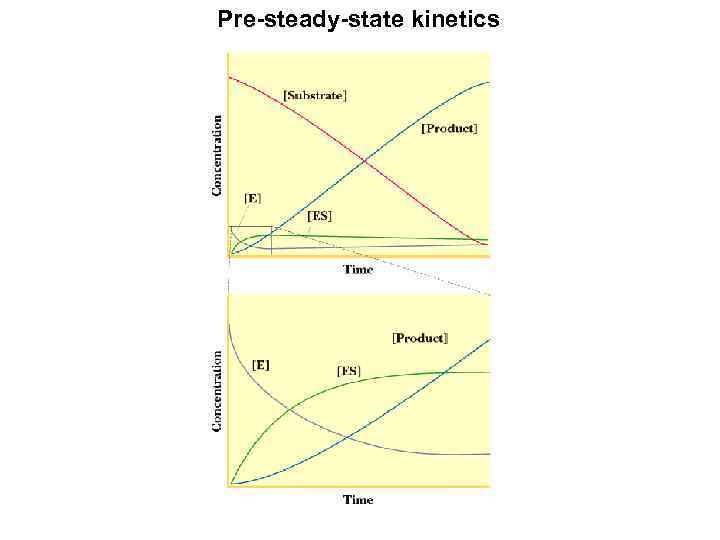 Pre-steady-state kinetics
Pre-steady-state kinetics
 Pre-steady-state kinetics
Pre-steady-state kinetics
![Титрование активных центров π π = [E]0 при [S]0>>Km(app) и k. I>>k. II Химотрипсин: Титрование активных центров π π = [E]0 при [S]0>>Km(app) и k. I>>k. II Химотрипсин:](https://present5.com/presentation/3540715_33786667/image-48.jpg) Титрование активных центров π π = [E]0 при [S]0>>Km(app) и k. I>>k. II Химотрипсин: циннамоил-имидазол, k. I = 1. 2 x 104 M-1 s-1 , k. II = 1. 3 x 10 -2 s-1. (Ref. JACS 88, 5890, 1966. )
Титрование активных центров π π = [E]0 при [S]0>>Km(app) и k. I>>k. II Химотрипсин: циннамоил-имидазол, k. I = 1. 2 x 104 M-1 s-1 , k. II = 1. 3 x 10 -2 s-1. (Ref. JACS 88, 5890, 1966. )
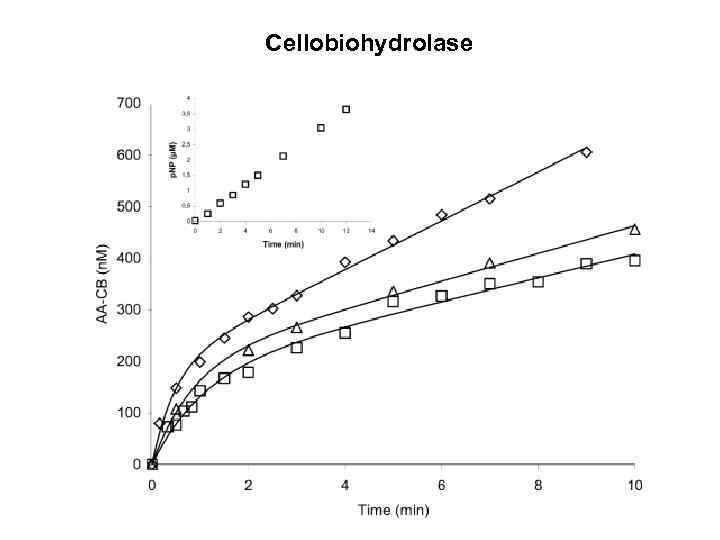 Cellobiohydrolase
Cellobiohydrolase
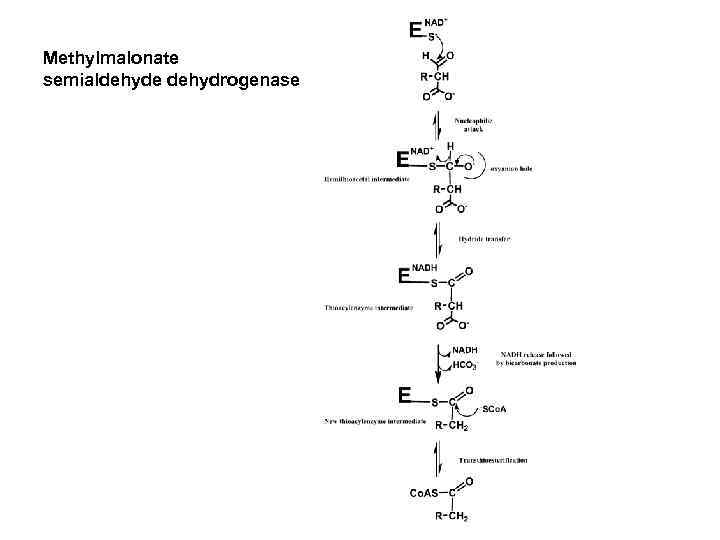 Мethylmalonate semialdehyde dehydrogenase
Мethylmalonate semialdehyde dehydrogenase
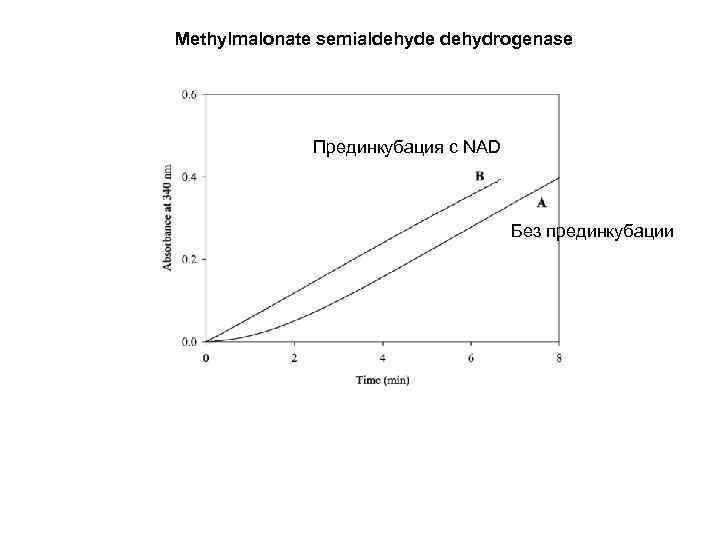 Мethylmalonate semialdehyde dehydrogenase Прединкубация с NAD Без прединкубации
Мethylmalonate semialdehyde dehydrogenase Прединкубация с NAD Без прединкубации
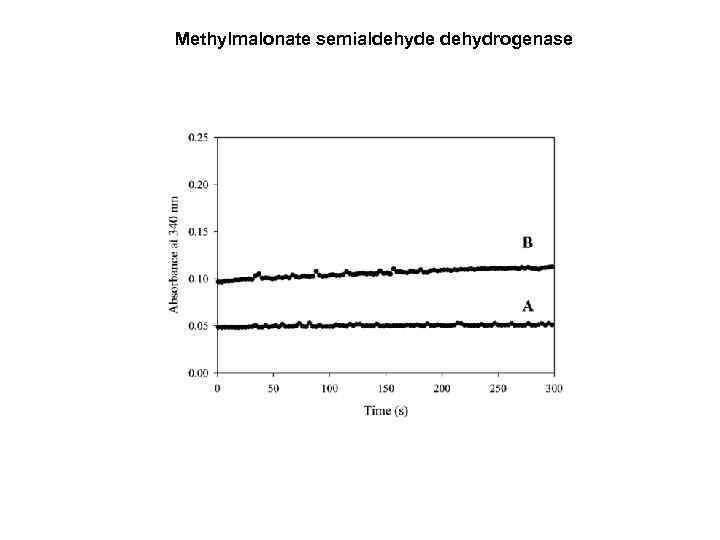 Мethylmalonate semialdehyde dehydrogenase
Мethylmalonate semialdehyde dehydrogenase
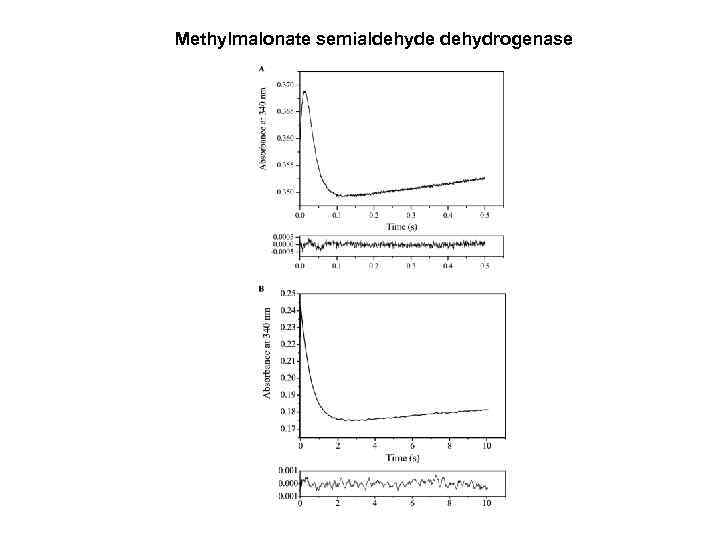 Мethylmalonate semialdehyde dehydrogenase
Мethylmalonate semialdehyde dehydrogenase
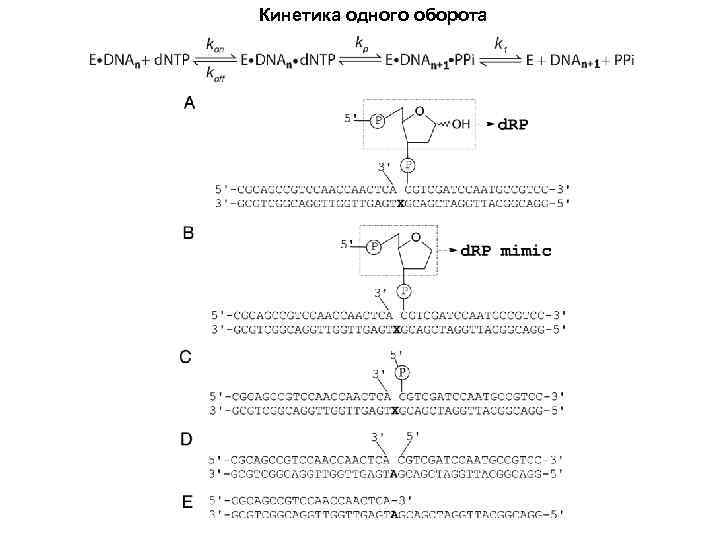 Кинетика одного оборота
Кинетика одного оборота
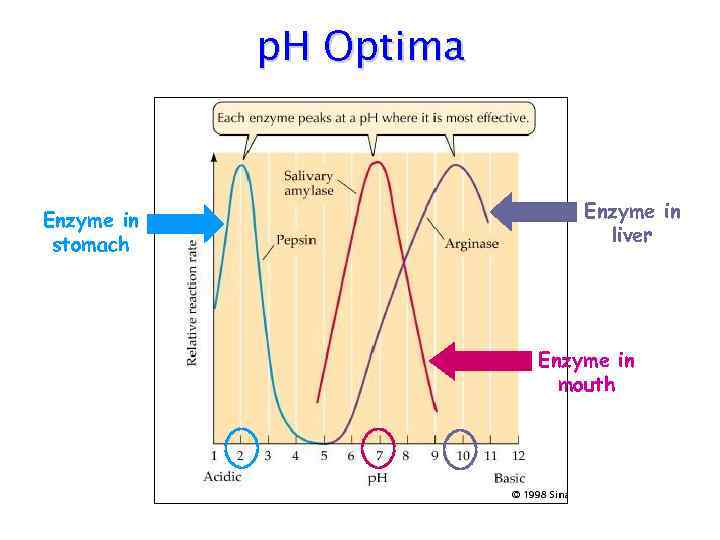 p. H Optima Enzyme in stomach Enzyme in liver Enzyme in mouth
p. H Optima Enzyme in stomach Enzyme in liver Enzyme in mouth
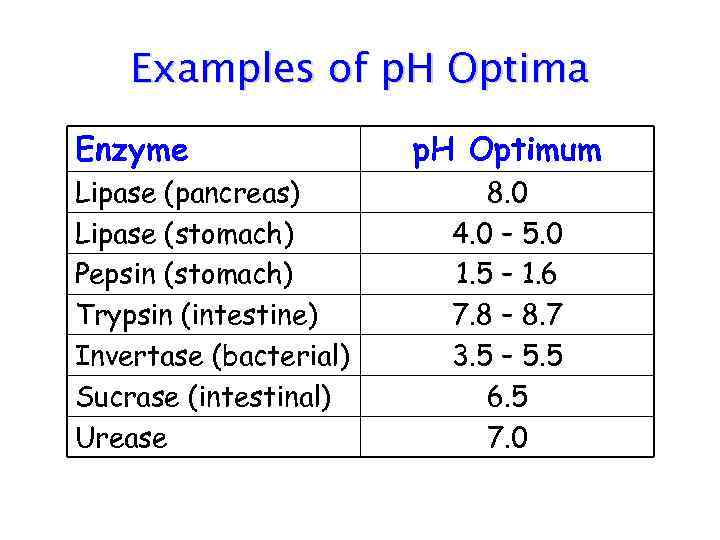 Examples of p. H Optima Enzyme Lipase (pancreas) Lipase (stomach) Pepsin (stomach) Trypsin (intestine) Invertase (bacterial) Sucrase (intestinal) Urease p. H Optimum 8. 0 4. 0 – 5. 0 1. 5 – 1. 6 7. 8 – 8. 7 3. 5 – 5. 5 6. 5 7. 0
Examples of p. H Optima Enzyme Lipase (pancreas) Lipase (stomach) Pepsin (stomach) Trypsin (intestine) Invertase (bacterial) Sucrase (intestinal) Urease p. H Optimum 8. 0 4. 0 – 5. 0 1. 5 – 1. 6 7. 8 – 8. 7 3. 5 – 5. 5 6. 5 7. 0
 How p. H Changes Affect Enzymes • May alter the binding of S to E (affects KM) • May alter the catalysis of bound S (affects kcat or Vmax) – Side chains necessary to catalysis must be in correct protonation state • May alter global protein conformation • May alter protonation state of substrate • May alter spectral properties of product
How p. H Changes Affect Enzymes • May alter the binding of S to E (affects KM) • May alter the catalysis of bound S (affects kcat or Vmax) – Side chains necessary to catalysis must be in correct protonation state • May alter global protein conformation • May alter protonation state of substrate • May alter spectral properties of product
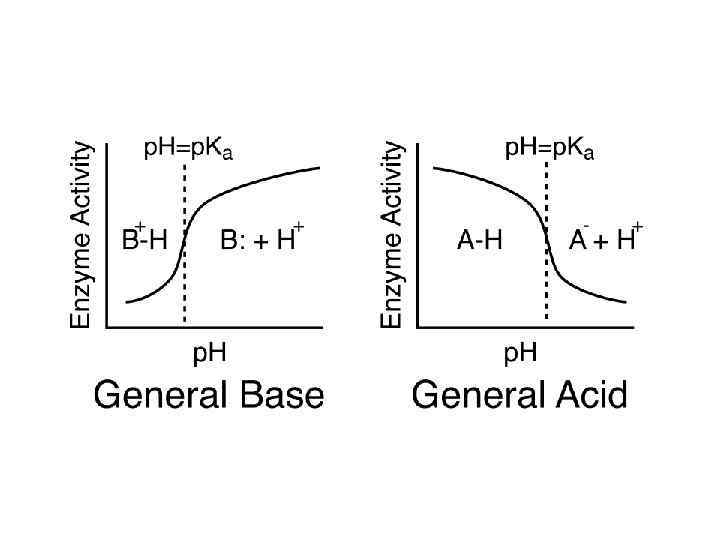
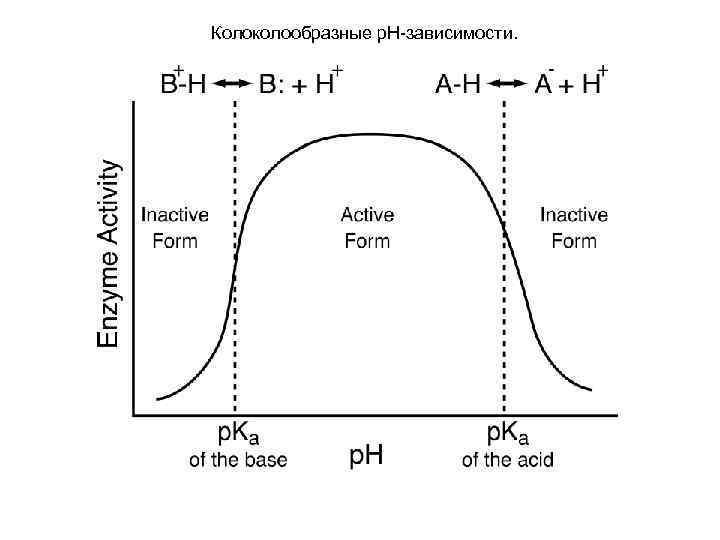 Колоколообразные р. Н-зависимости.
Колоколообразные р. Н-зависимости.
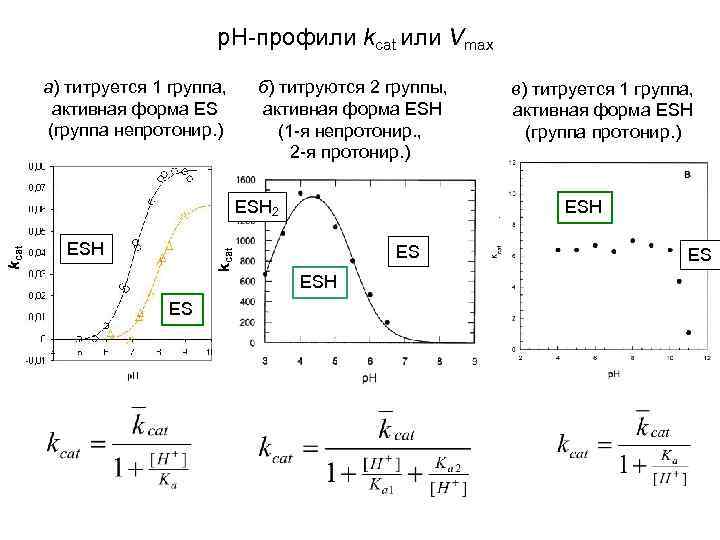 р. Н-профили kcat или Vmax а) титруется 1 группа, активная форма ЕS (группа непротонир. ) б) титруются 2 группы, активная форма ЕSН (1 -я непротонир. , 2 -я протонир. ) ЕSН kcat ЕSН 2 ЕS в) титруется 1 группа, активная форма ЕSН (группа протонир. ) ЕSН ЕS
р. Н-профили kcat или Vmax а) титруется 1 группа, активная форма ЕS (группа непротонир. ) б) титруются 2 группы, активная форма ЕSН (1 -я непротонир. , 2 -я протонир. ) ЕSН kcat ЕSН 2 ЕS в) титруется 1 группа, активная форма ЕSН (группа протонир. ) ЕSН ЕS
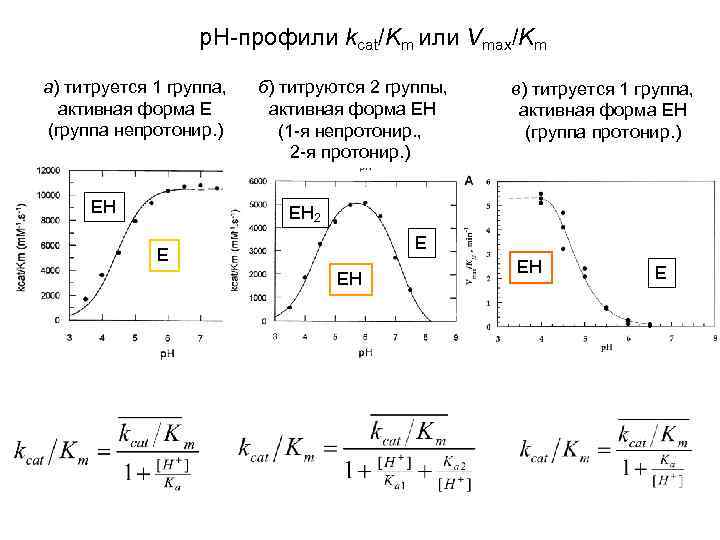 р. Н-профили kcat/Km или Vmax/Km а) титруется 1 группа, активная форма Е (группа непротонир. ) ЕН б) титруются 2 группы, активная форма ЕН (1 -я непротонир. , 2 -я протонир. ) в) титруется 1 группа, активная форма ЕН (группа протонир. ) ЕН 2 Е Е ЕН ЕН Е
р. Н-профили kcat/Km или Vmax/Km а) титруется 1 группа, активная форма Е (группа непротонир. ) ЕН б) титруются 2 группы, активная форма ЕН (1 -я непротонир. , 2 -я протонир. ) в) титруется 1 группа, активная форма ЕН (группа протонир. ) ЕН 2 Е Е ЕН ЕН Е
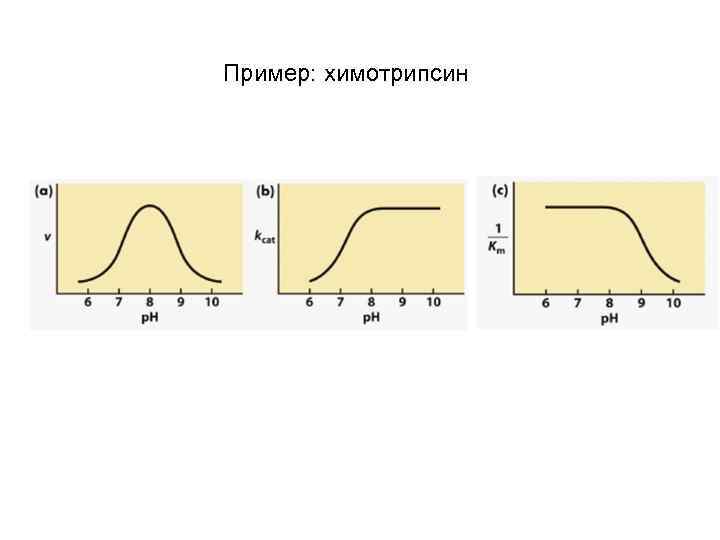 Пример: химотрипсин
Пример: химотрипсин
 Базовая схема р. Н-зависимости кинетических параметров. * Связывание S тоже может зависеть от его р. Н-формы в Km и kcat/Km включается fs
Базовая схема р. Н-зависимости кинетических параметров. * Связывание S тоже может зависеть от его р. Н-формы в Km и kcat/Km включается fs
 Пример вывода уравнения р. Н-зависимости (пенициллаза).
Пример вывода уравнения р. Н-зависимости (пенициллаза).
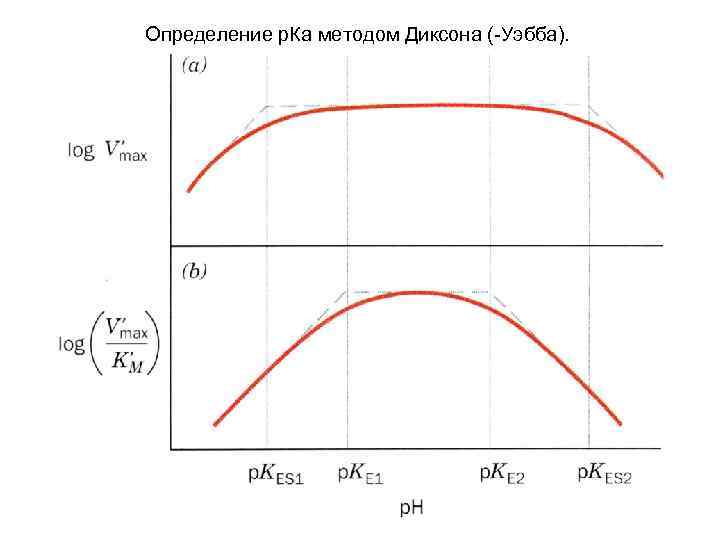 Определение р. Ка методом Диксона (-Уэбба).
Определение р. Ка методом Диксона (-Уэбба).
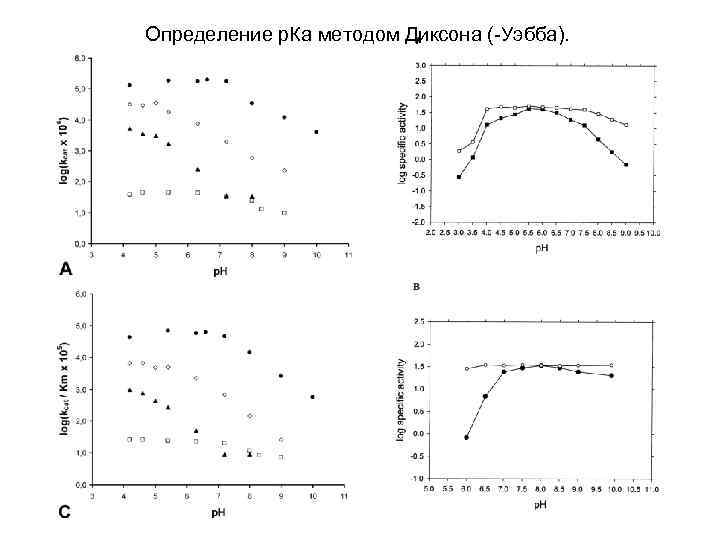 Определение р. Ка методом Диксона (-Уэбба).
Определение р. Ка методом Диксона (-Уэбба).
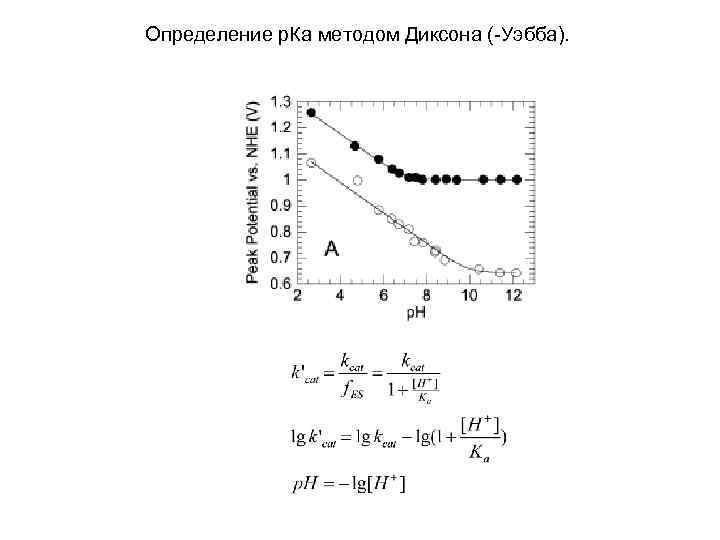 Определение р. Ка методом Диксона (-Уэбба).
Определение р. Ка методом Диксона (-Уэбба).
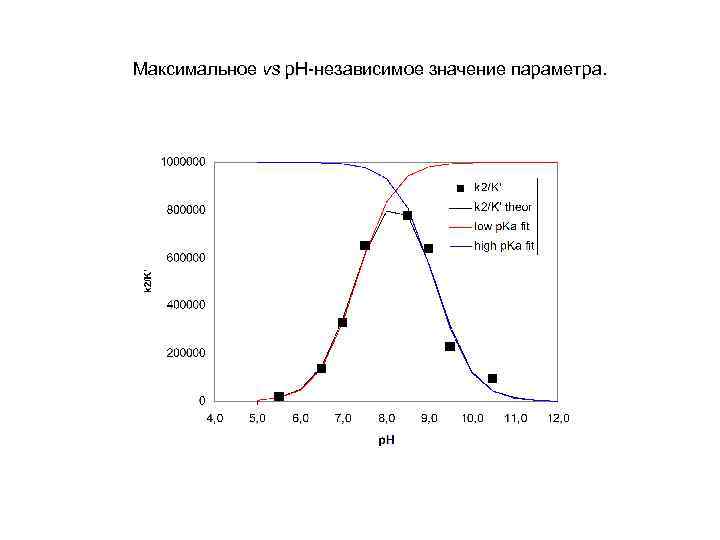 Максимальное vs р. Н-независимое значение параметра.
Максимальное vs р. Н-независимое значение параметра.
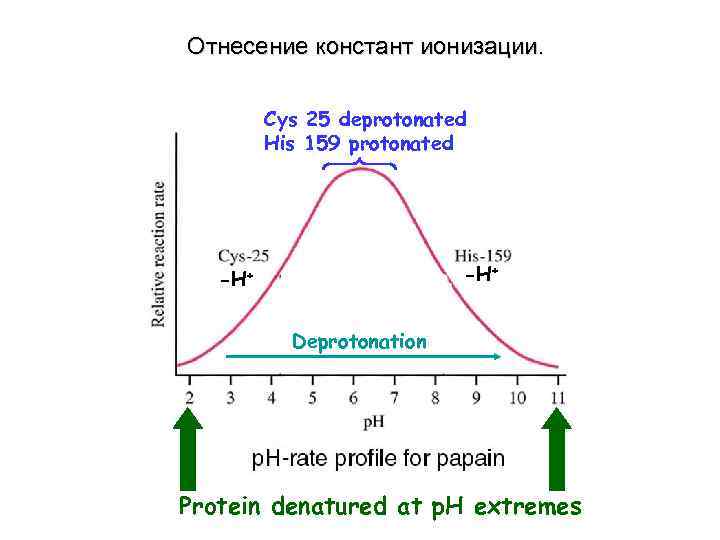 Отнесение констант ионизации. Cys 25 deprotonated His 159 protonated -H+ Deprotonation Protein denatured at p. H extremes
Отнесение констант ионизации. Cys 25 deprotonated His 159 protonated -H+ Deprotonation Protein denatured at p. H extremes
 Типичные значения р. Ка групп белков (используемые по умолчанию в расчетных программах). Amino Acid Asp Glu Arg p. Ka 3. 0 - 4. 7 (4. 0) 3. 0 – 4. 7 (4. 4) 11. 6 – 12. 6 (12. 0) Lys His Cys(-SH) Tyr 7. 6 – 10. 6 (9. 0) 5. 6 – 7. 0 (6. 08) 8. 3 – 8. 6 (8. 28) 9. 8 – 10. 4 (9. 84)
Типичные значения р. Ка групп белков (используемые по умолчанию в расчетных программах). Amino Acid Asp Glu Arg p. Ka 3. 0 - 4. 7 (4. 0) 3. 0 – 4. 7 (4. 4) 11. 6 – 12. 6 (12. 0) Lys His Cys(-SH) Tyr 7. 6 – 10. 6 (9. 0) 5. 6 – 7. 0 (6. 08) 8. 3 – 8. 6 (8. 28) 9. 8 – 10. 4 (9. 84)
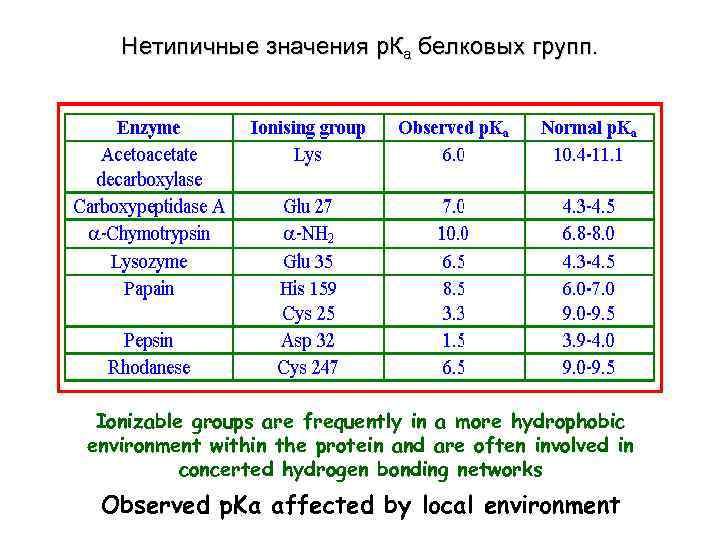 Нетипичные значения р. Ка белковых групп. Ionizable groups are frequently in a more hydrophobic environment within the protein and are often involved in concerted hydrogen bonding networks Observed p. Ka affected by local environment
Нетипичные значения р. Ка белковых групп. Ionizable groups are frequently in a more hydrophobic environment within the protein and are often involved in concerted hydrogen bonding networks Observed p. Ka affected by local environment
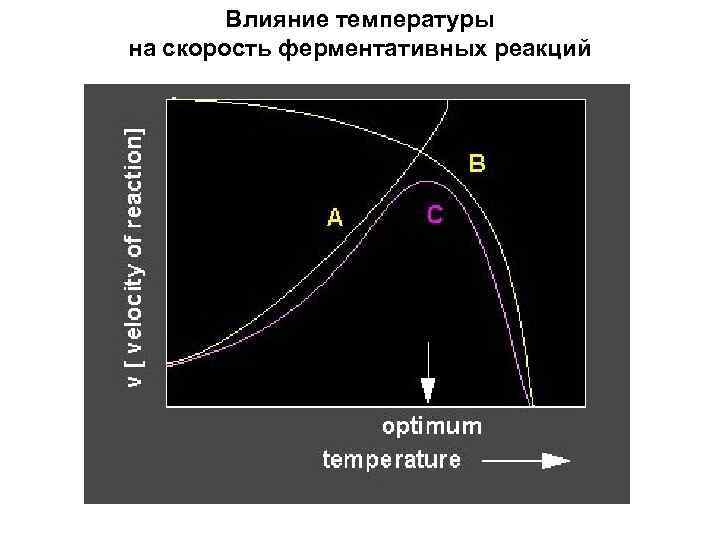 Влияние температуры на скорость ферментативных реакций
Влияние температуры на скорость ферментативных реакций
 Ингибирование: 1. Необратимое ингибирование
Ингибирование: 1. Необратимое ингибирование
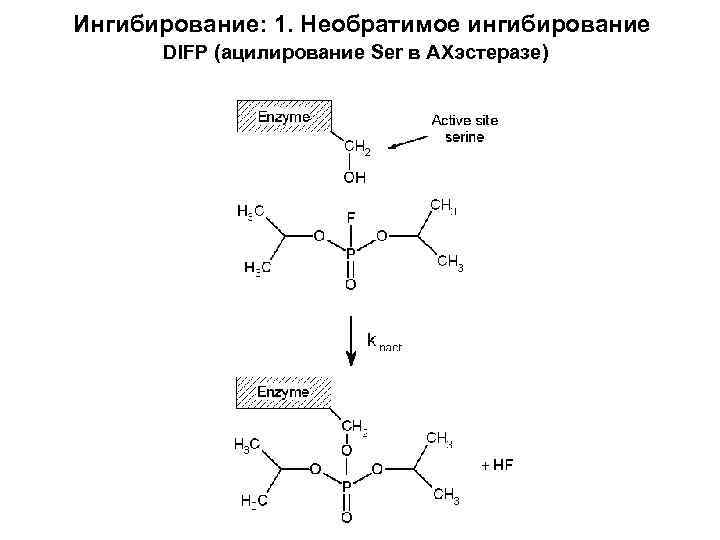 Ингибирование: 1. Необратимое ингибирование DIFP (ацилирование Ser в АХэстеразе)
Ингибирование: 1. Необратимое ингибирование DIFP (ацилирование Ser в АХэстеразе)
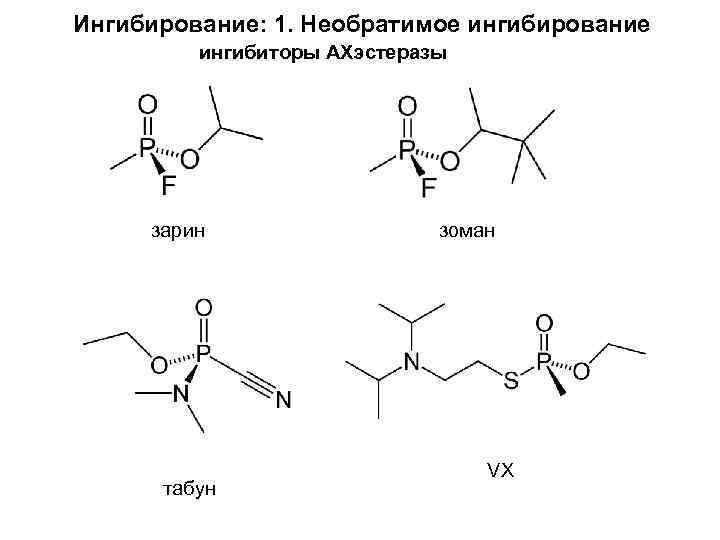 Ингибирование: 1. Необратимое ингибирование ингибиторы АХэстеразы зарин табун зоман VX
Ингибирование: 1. Необратимое ингибирование ингибиторы АХэстеразы зарин табун зоман VX
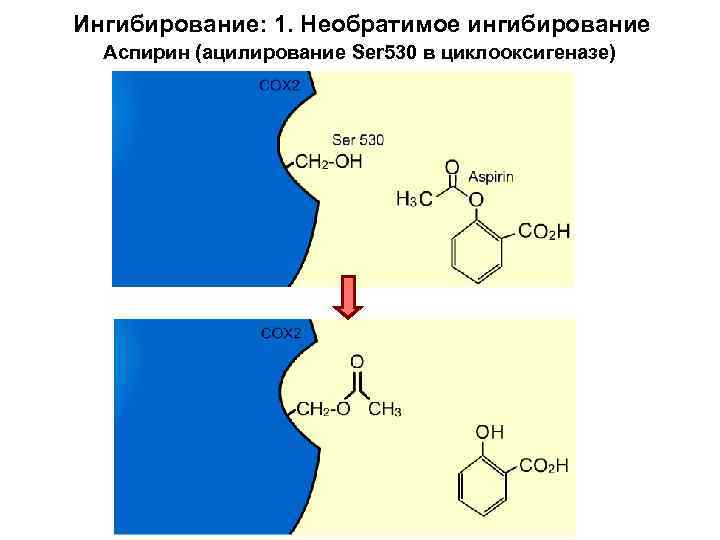 Ингибирование: 1. Необратимое ингибирование Аспирин (ацилирование Ser 530 в циклооксигеназе)
Ингибирование: 1. Необратимое ингибирование Аспирин (ацилирование Ser 530 в циклооксигеназе)
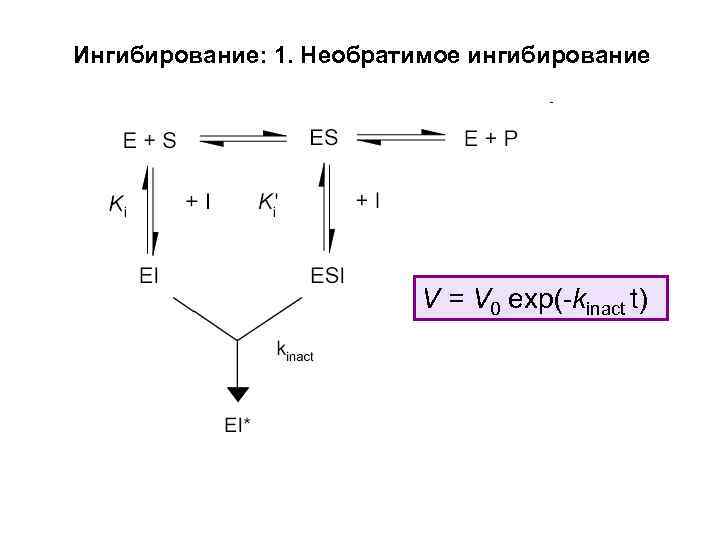 Ингибирование: 1. Необратимое ингибирование V = V 0 exp(-kinact t)
Ингибирование: 1. Необратимое ингибирование V = V 0 exp(-kinact t)
![Ингибирование: 1. Необратимое ингибирование Зависимость 1/kapp от 1/[I] Ингибирование: 1. Необратимое ингибирование Зависимость 1/kapp от 1/[I]](https://present5.com/presentation/3540715_33786667/image-78.jpg) Ингибирование: 1. Необратимое ингибирование Зависимость 1/kapp от 1/[I]
Ингибирование: 1. Необратимое ингибирование Зависимость 1/kapp от 1/[I]
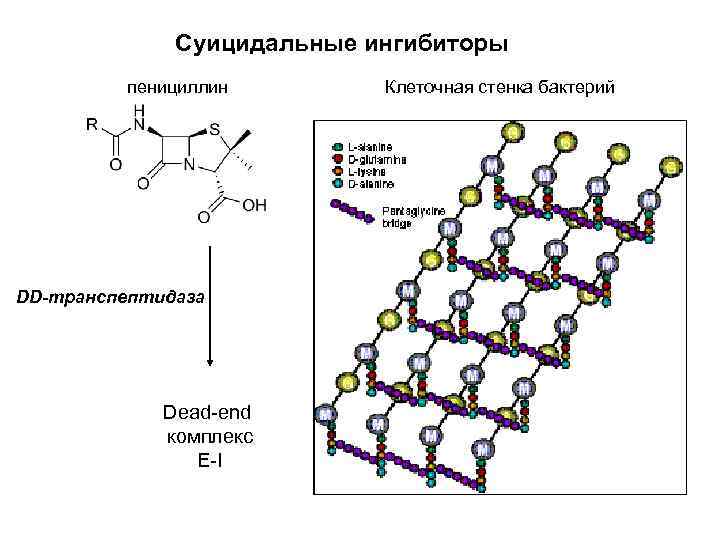 Суицидальные ингибиторы пенициллин DD-транспептидаза Dead-end комплекс Е-I Клеточная стенка бактерий
Суицидальные ингибиторы пенициллин DD-транспептидаза Dead-end комплекс Е-I Клеточная стенка бактерий
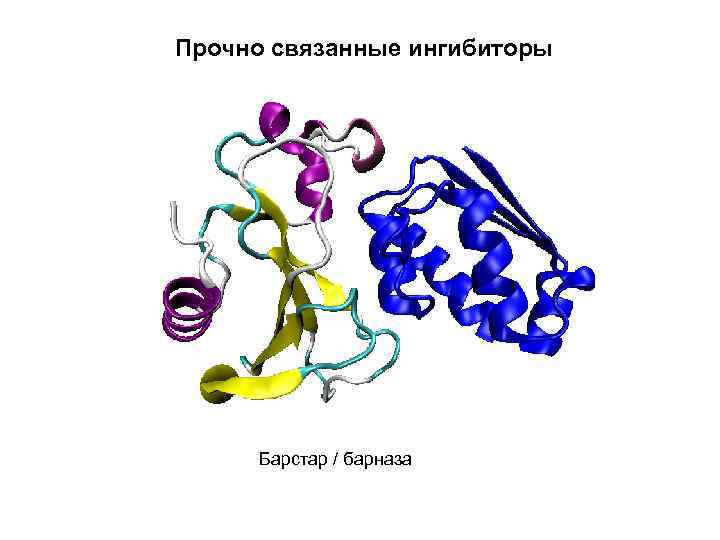 Прочно связанные ингибиторы Барстар / барназа
Прочно связанные ингибиторы Барстар / барназа
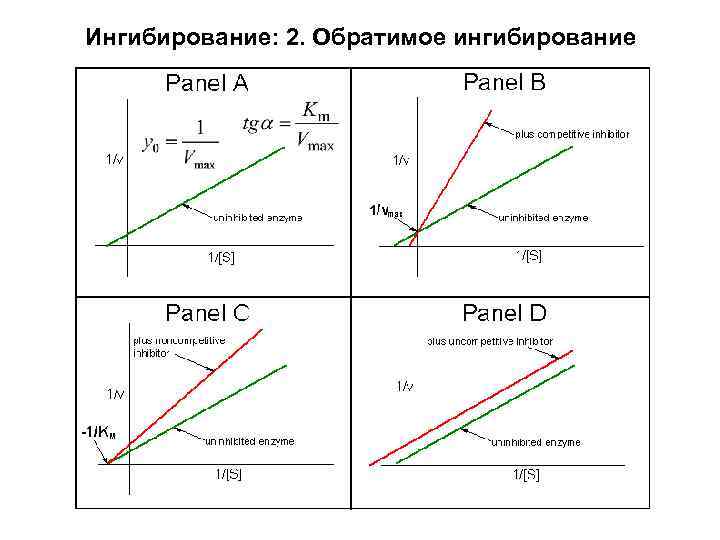 Ингибирование: 2. Обратимое ингибирование
Ингибирование: 2. Обратимое ингибирование
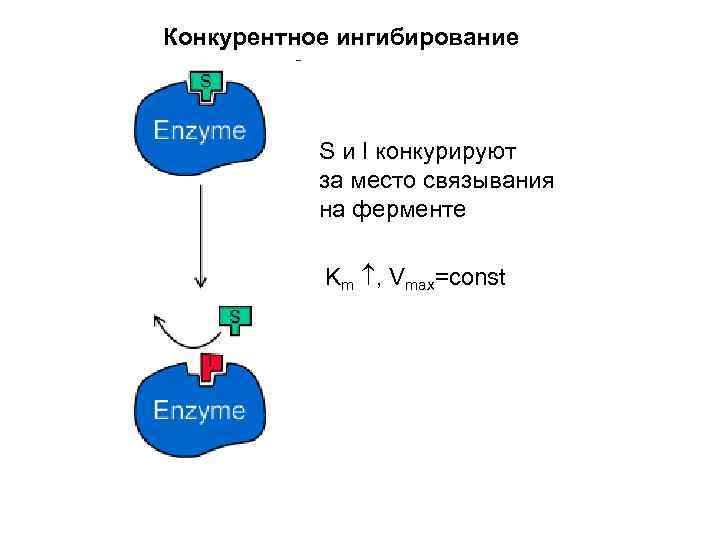 Конкурентное ингибирование S и I конкурируют за место связывания на ферменте Km , Vmax=const
Конкурентное ингибирование S и I конкурируют за место связывания на ферменте Km , Vmax=const
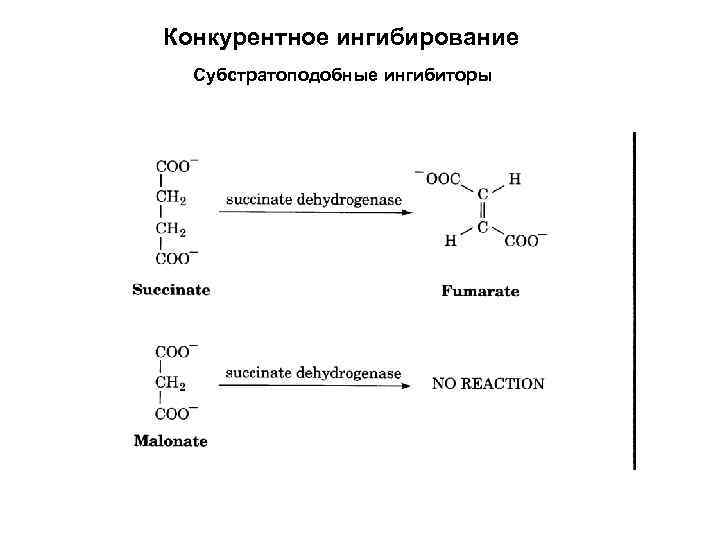 Конкурентное ингибирование Субстратоподобные ингибиторы
Конкурентное ингибирование Субстратоподобные ингибиторы
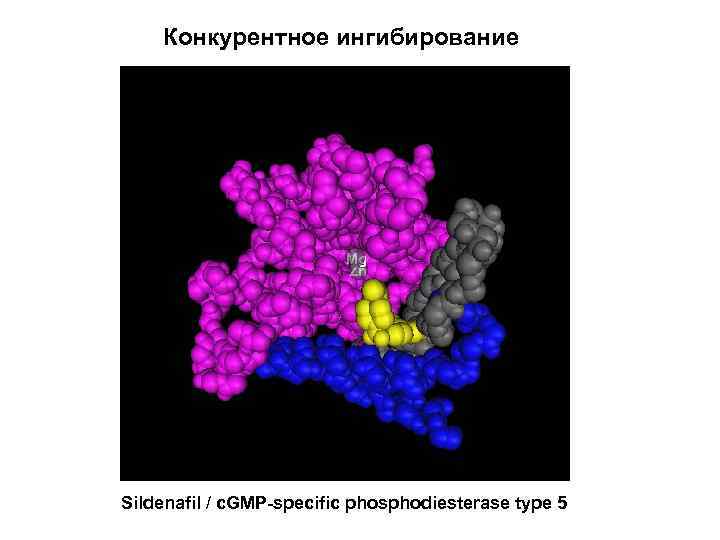 Конкурентное ингибирование Sildenafil / c. GMP-specific phosphodiesterase type 5
Конкурентное ингибирование Sildenafil / c. GMP-specific phosphodiesterase type 5
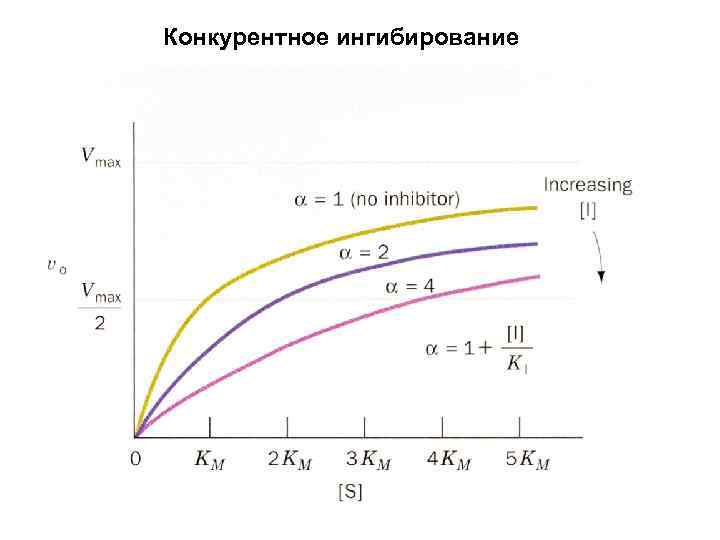 Конкурентное ингибирование
Конкурентное ингибирование
 Конкурентное ингибирование
Конкурентное ингибирование
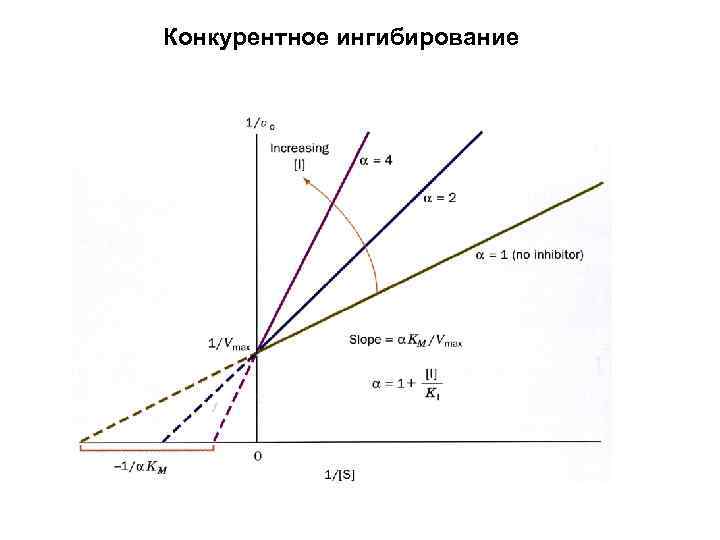 Конкурентное ингибирование
Конкурентное ингибирование
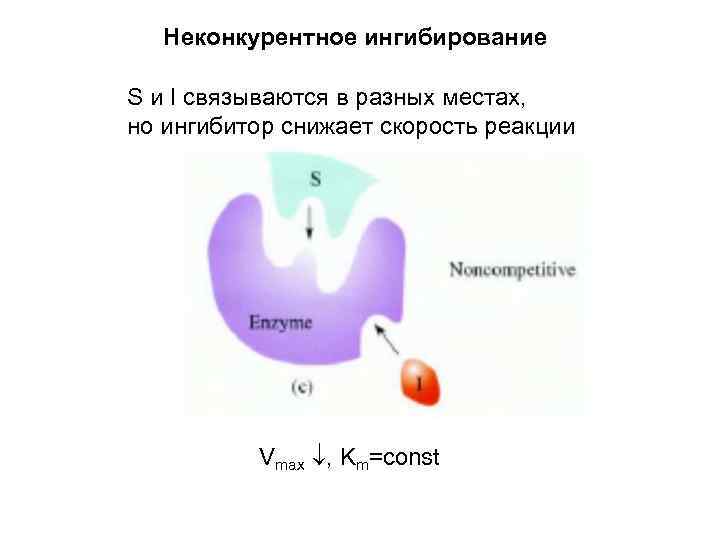 Неконкурентное ингибирование S и I связываются в разных местах, но ингибитор снижает скорость реакции Vmax , Km=const
Неконкурентное ингибирование S и I связываются в разных местах, но ингибитор снижает скорость реакции Vmax , Km=const
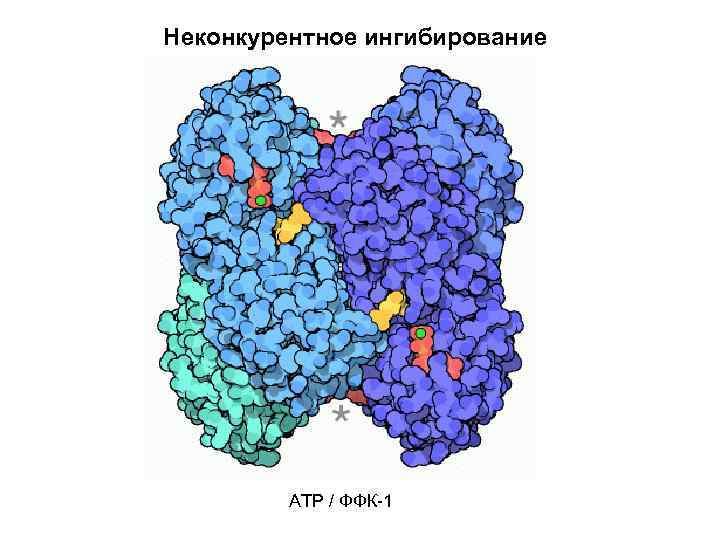 Неконкурентное ингибирование ATP / ФФК-1
Неконкурентное ингибирование ATP / ФФК-1
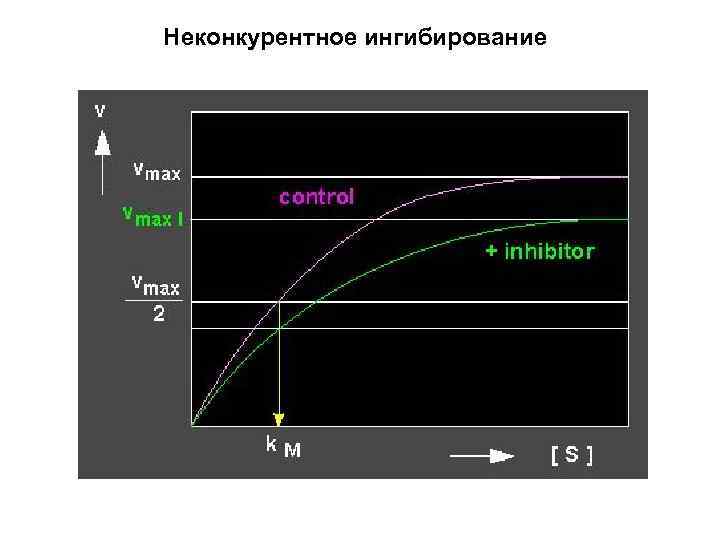 Неконкурентное ингибирование
Неконкурентное ингибирование
 Неконкурентное ингибирование
Неконкурентное ингибирование
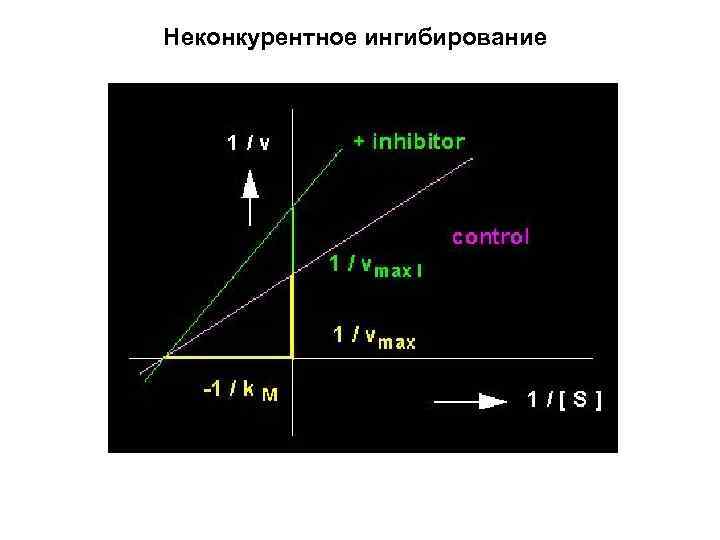 Неконкурентное ингибирование
Неконкурентное ингибирование
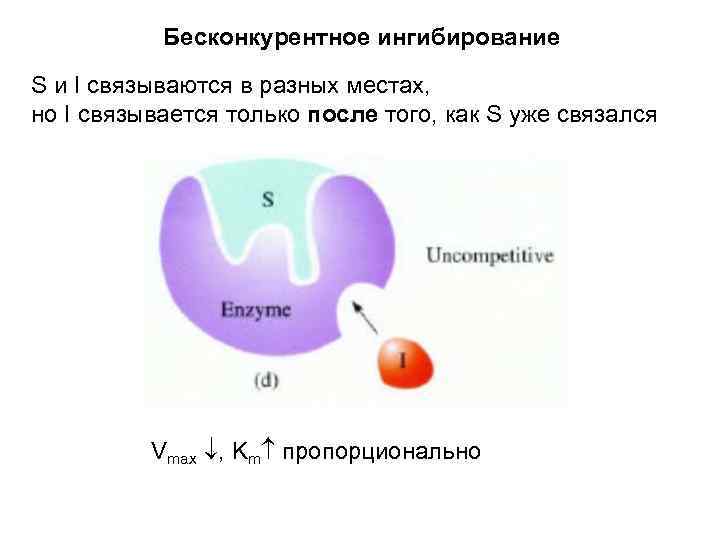 Бесконкурентное ингибирование S и I связываются в разных местах, но I связывается только после того, как S уже связался Vmax , Km пропорционально
Бесконкурентное ингибирование S и I связываются в разных местах, но I связывается только после того, как S уже связался Vmax , Km пропорционально
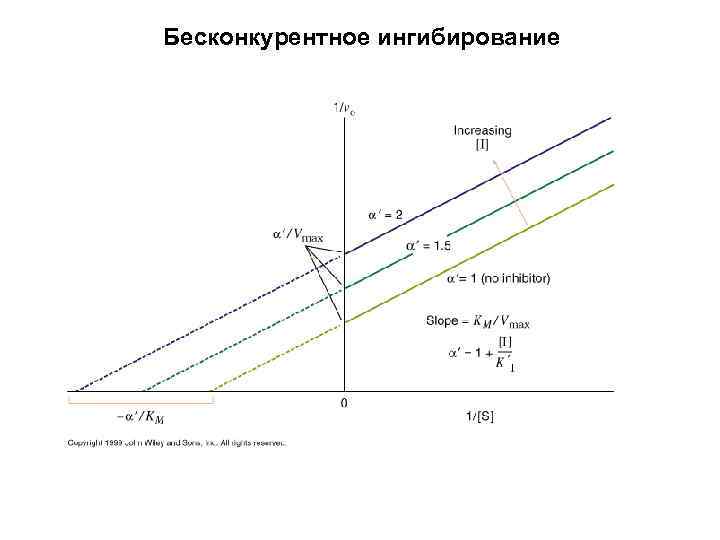
 Бесконкурентное ингибирование
Бесконкурентное ингибирование
 Бесконкурентное ингибирование
Бесконкурентное ингибирование
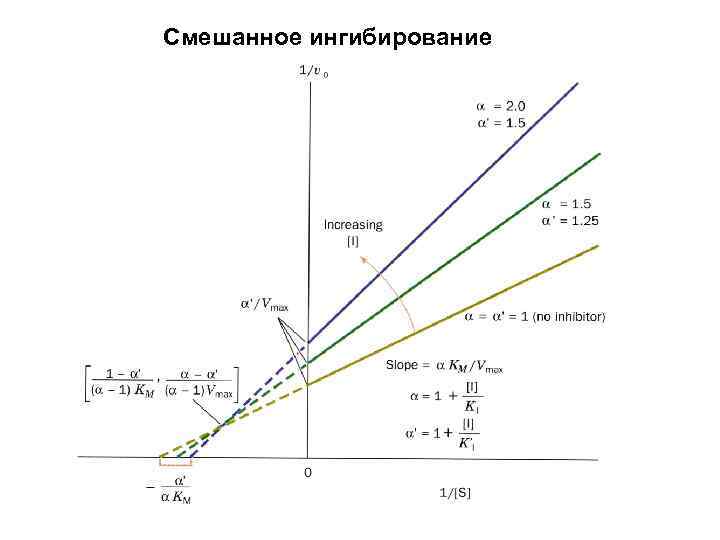 Смешанное ингибирование
Смешанное ингибирование
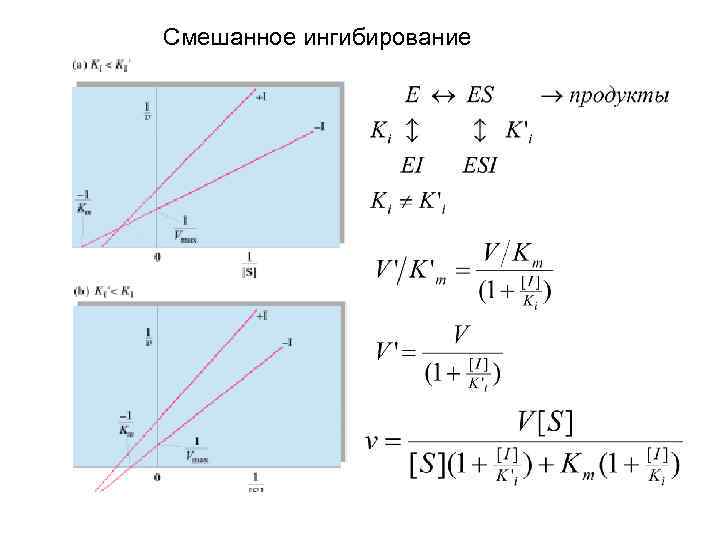 Смешанное ингибирование
Смешанное ингибирование
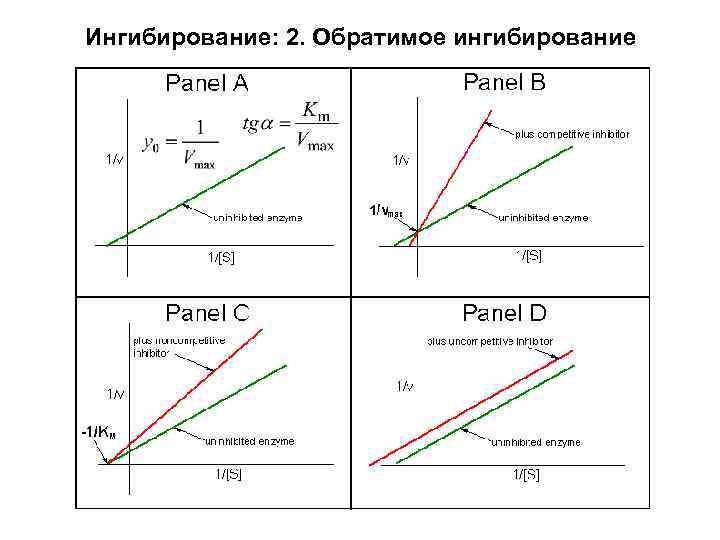 Ингибирование: 2. Обратимое ингибирование
Ингибирование: 2. Обратимое ингибирование
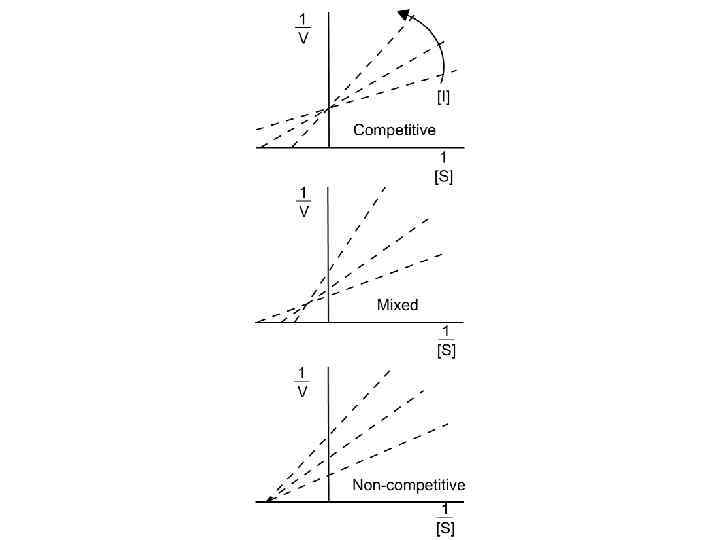
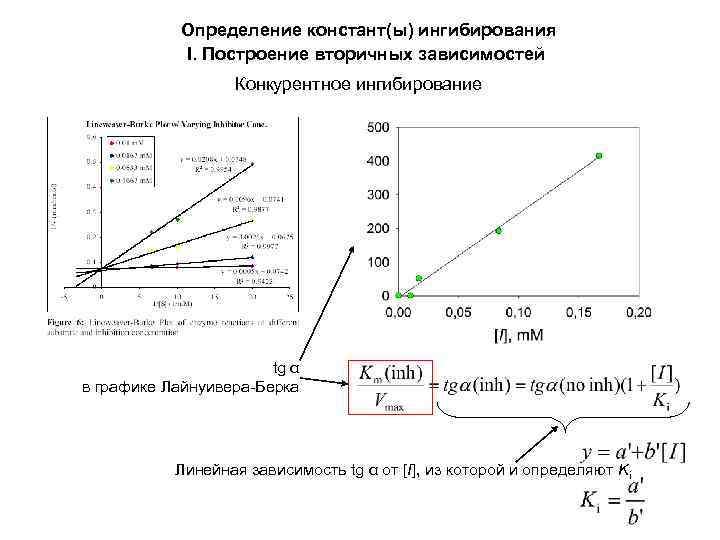 Определение констант(ы) ингибирования I. Построение вторичных зависимостей Конкурентное ингибирование tg α в графике Лайнуивера-Берка Линейная зависимость tg α от [I], из которой и определяют Ki
Определение констант(ы) ингибирования I. Построение вторичных зависимостей Конкурентное ингибирование tg α в графике Лайнуивера-Берка Линейная зависимость tg α от [I], из которой и определяют Ki
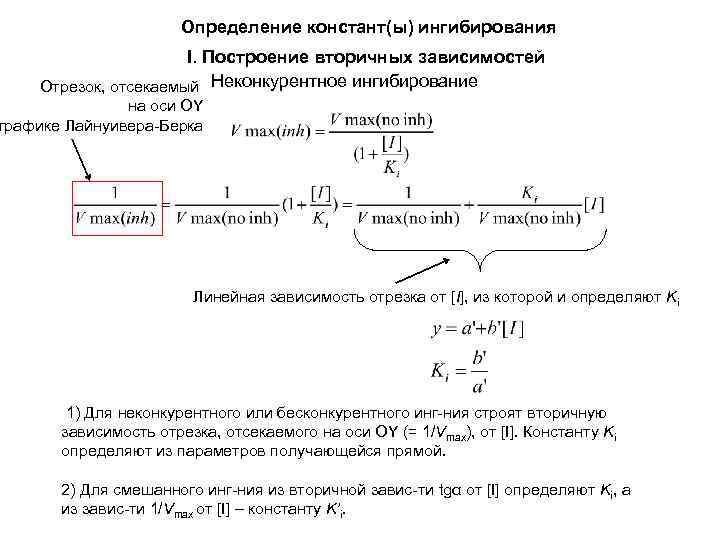 Определение констант(ы) ингибирования I. Построение вторичных зависимостей Отрезок, отсекаемый Неконкурентное ингибирование на оси OY графике Лайнуивера-Берка Линейная зависимость отрезка от [I], из которой и определяют Ki 1) Для неконкурентного или бесконкурентного инг-ния строят вторичную зависимость отрезка, отсекаемого на оси OY (= 1/Vmax), от [I]. Константу Ki определяют из параметров получающейся прямой. 2) Для смешанного инг-ния из вторичной завис-ти tgα от [I] определяют Ki, а из завис-ти 1/Vmax от [I] – константу K’i.
Определение констант(ы) ингибирования I. Построение вторичных зависимостей Отрезок, отсекаемый Неконкурентное ингибирование на оси OY графике Лайнуивера-Берка Линейная зависимость отрезка от [I], из которой и определяют Ki 1) Для неконкурентного или бесконкурентного инг-ния строят вторичную зависимость отрезка, отсекаемого на оси OY (= 1/Vmax), от [I]. Константу Ki определяют из параметров получающейся прямой. 2) Для смешанного инг-ния из вторичной завис-ти tgα от [I] определяют Ki, а из завис-ти 1/Vmax от [I] – константу K’i.
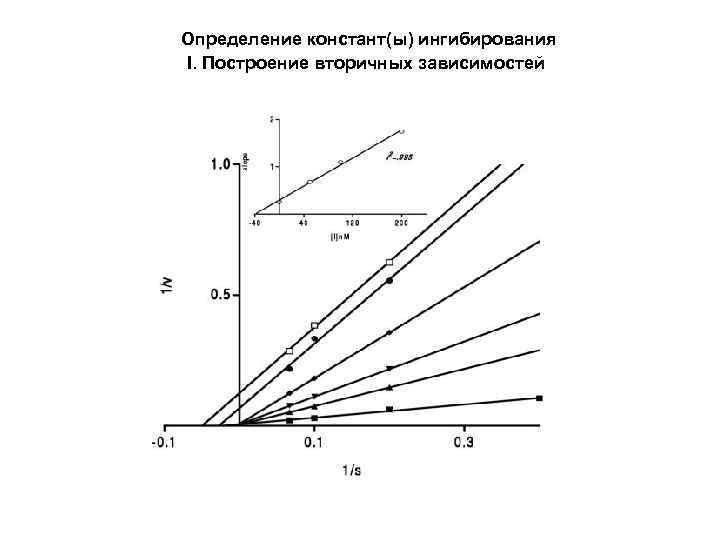 Определение констант(ы) ингибирования I. Построение вторичных зависимостей
Определение констант(ы) ингибирования I. Построение вторичных зависимостей
![1/v Определение констант(ы) ингибирования II. Преобразование Диксона Ki [I] 1/v Определение констант(ы) ингибирования II. Преобразование Диксона Ki [I]](https://present5.com/presentation/3540715_33786667/image-102.jpg) 1/v Определение констант(ы) ингибирования II. Преобразование Диксона Ki [I]
1/v Определение констант(ы) ингибирования II. Преобразование Диксона Ki [I]
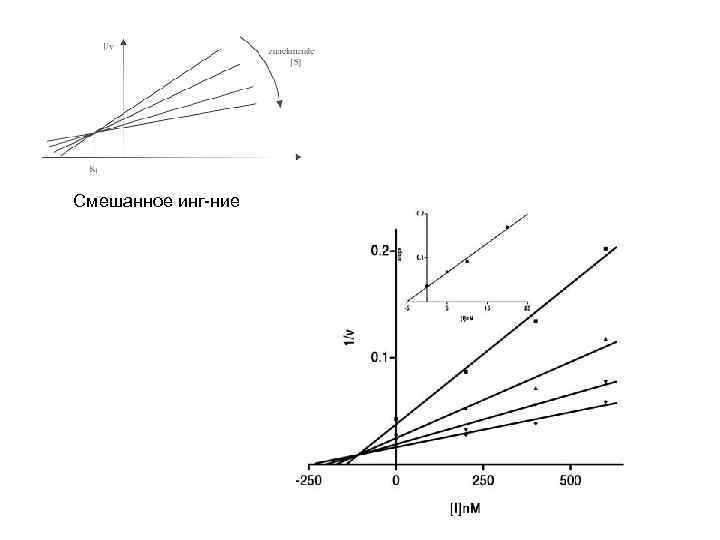 Смешанное инг-ние
Смешанное инг-ние
 Для тренировки
Для тренировки
 Для тренировки
Для тренировки
 Для тренировки
Для тренировки
 Drug design Random selection rational
Drug design Random selection rational
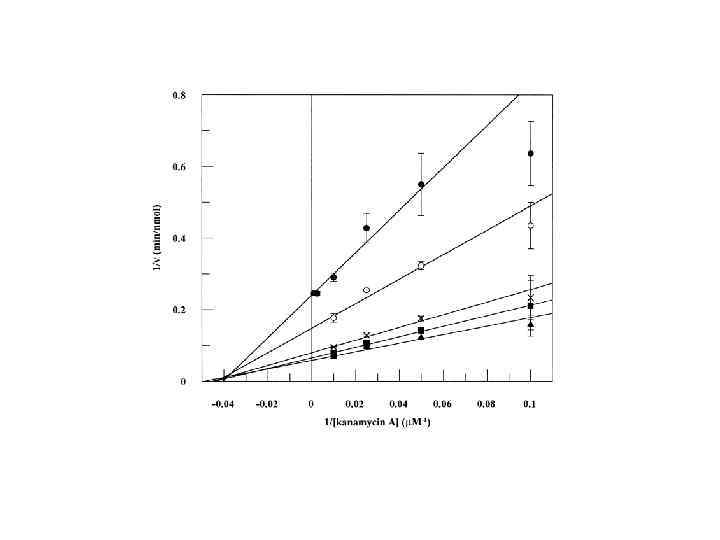
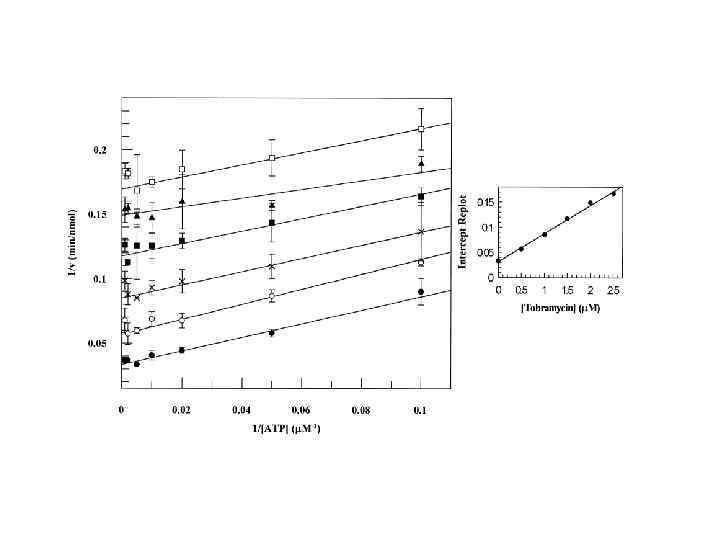
 Двухсубстратные реакции
Двухсубстратные реакции
![Примеры двухсубстратных реакций/ферментов glutathione S-transferase, [19] dihydrofolate reductase[20] DNA polymerase. [21] thioredoxin peroxidase, [22] Примеры двухсубстратных реакций/ферментов glutathione S-transferase, [19] dihydrofolate reductase[20] DNA polymerase. [21] thioredoxin peroxidase, [22]](https://present5.com/presentation/3540715_33786667/image-110.jpg) Примеры двухсубстратных реакций/ферментов glutathione S-transferase, [19] dihydrofolate reductase[20] DNA polymerase. [21] thioredoxin peroxidase, [22] acylneuraminate cytydilyltransferase[23], trypsin and chymotrypsin. [24]
Примеры двухсубстратных реакций/ферментов glutathione S-transferase, [19] dihydrofolate reductase[20] DNA polymerase. [21] thioredoxin peroxidase, [22] acylneuraminate cytydilyltransferase[23], trypsin and chymotrypsin. [24]
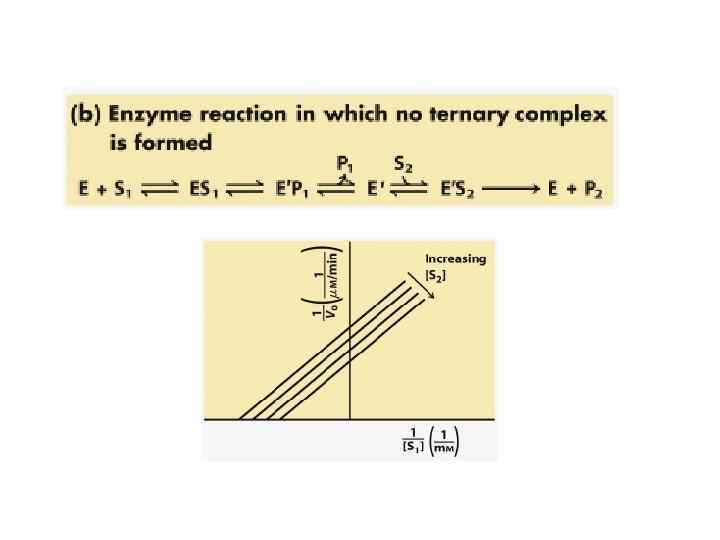
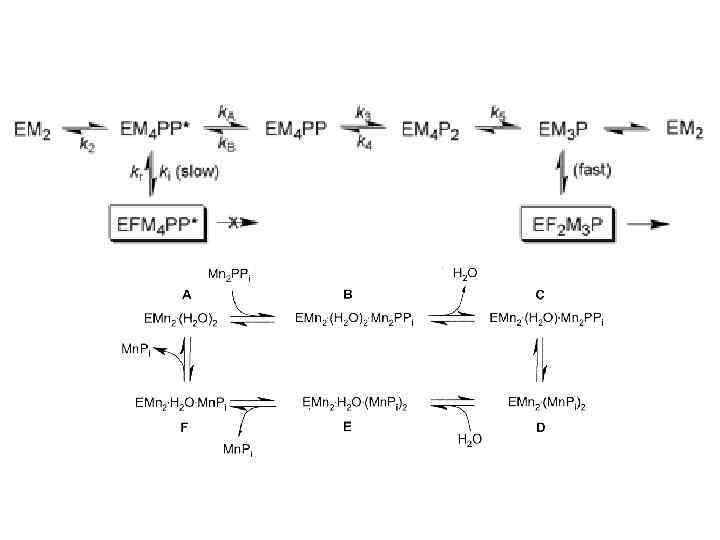
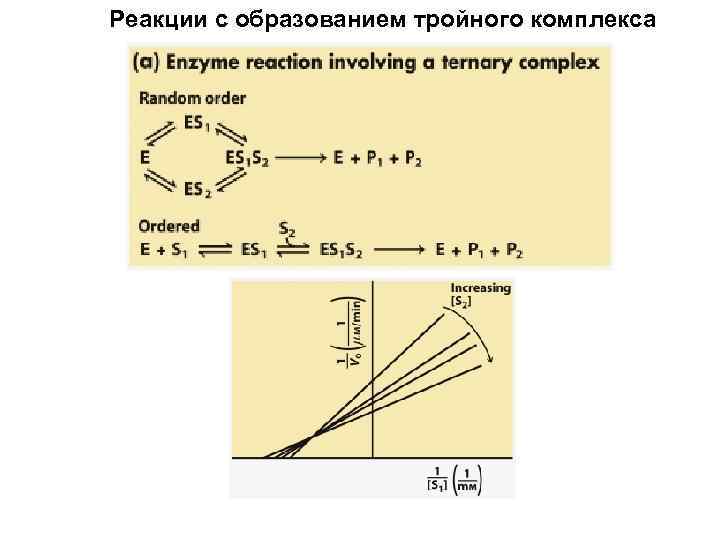 Реакции с образованием тройного комплекса
Реакции с образованием тройного комплекса



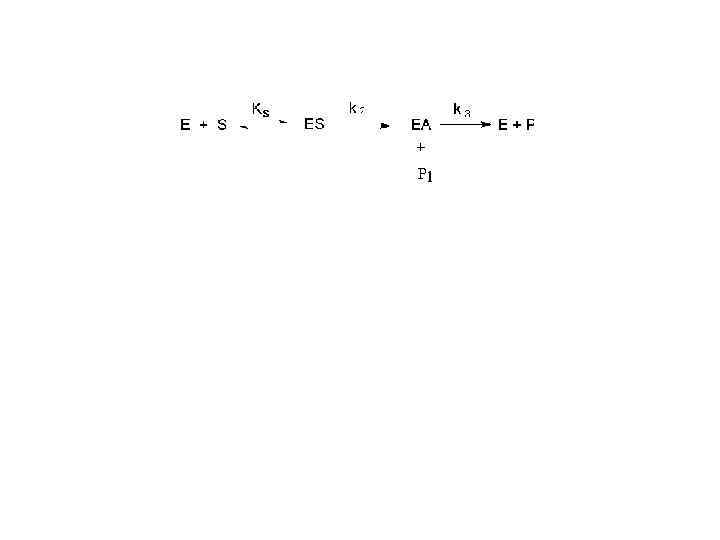
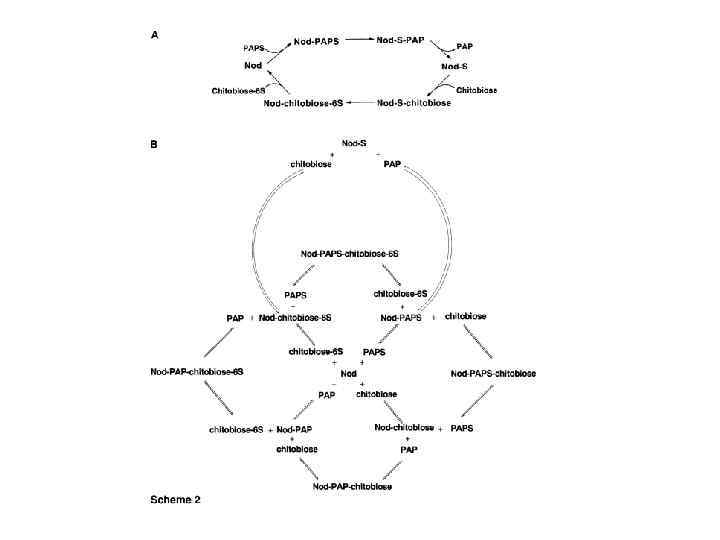

 Scheme 1. Proposed catalytic mechanism (2, 3) Stetefeld, J. et al. (2006) Proc. Natl. Acad. Sci. USA 103, 13688 -13693 Copyright © 2006 by the National Academy of Sciences
Scheme 1. Proposed catalytic mechanism (2, 3) Stetefeld, J. et al. (2006) Proc. Natl. Acad. Sci. USA 103, 13688 -13693 Copyright © 2006 by the National Academy of Sciences
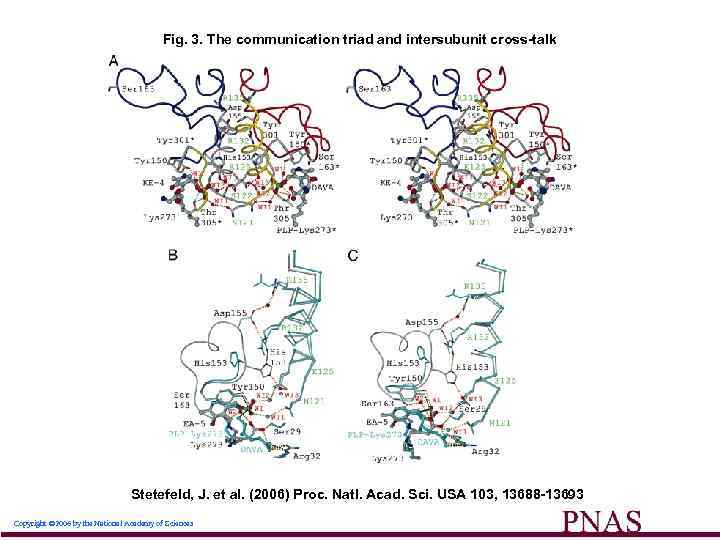 Fig. 3. The communication triad and intersubunit cross-talk Stetefeld, J. et al. (2006) Proc. Natl. Acad. Sci. USA 103, 13688 -13693 Copyright © 2006 by the National Academy of Sciences
Fig. 3. The communication triad and intersubunit cross-talk Stetefeld, J. et al. (2006) Proc. Natl. Acad. Sci. USA 103, 13688 -13693 Copyright © 2006 by the National Academy of Sciences
![Bacteriophage T 4 Dam DNA-[N 6 -adenine]Methyltransferase kmeth = 0. 56 s 1 kcat Bacteriophage T 4 Dam DNA-[N 6 -adenine]Methyltransferase kmeth = 0. 56 s 1 kcat](https://present5.com/presentation/3540715_33786667/image-130.jpg) Bacteriophage T 4 Dam DNA-[N 6 -adenine]Methyltransferase kmeth = 0. 56 s 1 kcat = 0. 015 s 1
Bacteriophage T 4 Dam DNA-[N 6 -adenine]Methyltransferase kmeth = 0. 56 s 1 kcat = 0. 015 s 1
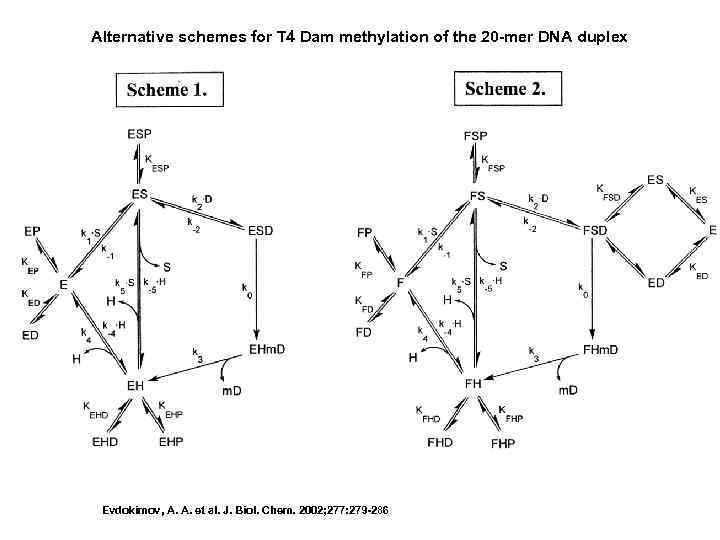 Alternative schemes for T 4 Dam methylation of the 20 -mer DNA duplex Evdokimov, A. A. et al. J. Biol. Chem. 2002; 277: 279 -286
Alternative schemes for T 4 Dam methylation of the 20 -mer DNA duplex Evdokimov, A. A. et al. J. Biol. Chem. 2002; 277: 279 -286
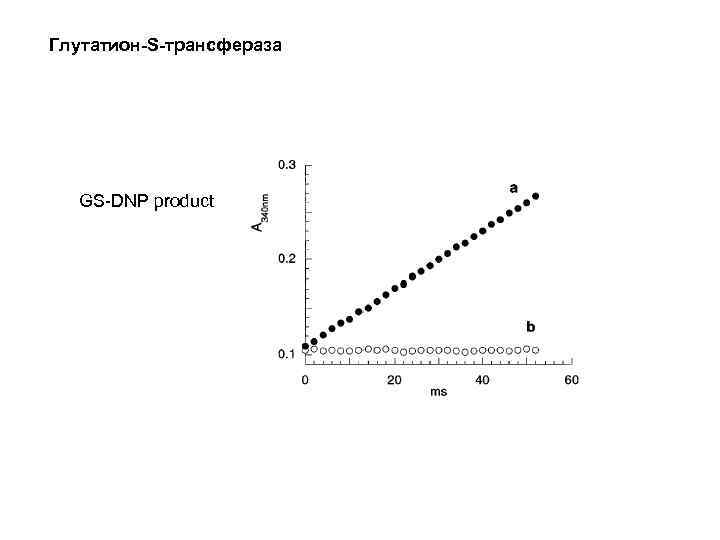 Глутатион-S-трансфераза GS-DNP product
Глутатион-S-трансфераза GS-DNP product
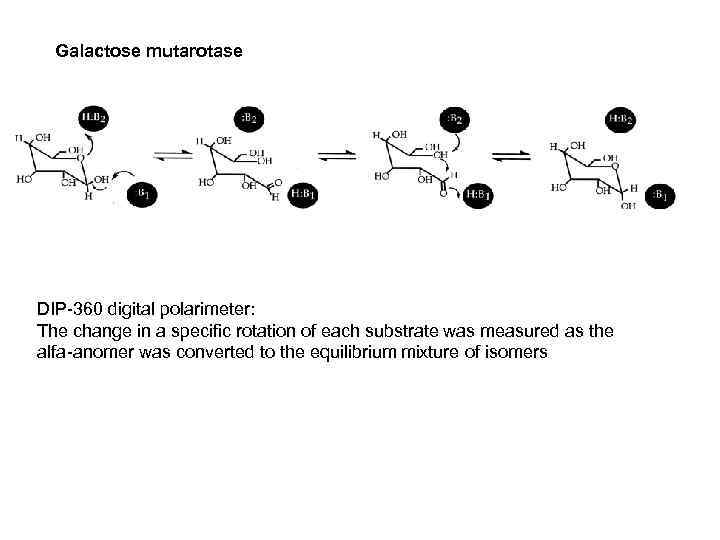 Galactose mutarotase DIP-360 digital polarimeter: The change in a specific rotation of each substrate was measured as the alfa -anomer was converted to the equilibrium mixture of isomers
Galactose mutarotase DIP-360 digital polarimeter: The change in a specific rotation of each substrate was measured as the alfa -anomer was converted to the equilibrium mixture of isomers
 Rectangular hyperbolic plot (h = Hill coefficient) where h = 1 for a MM enzyme Hill plot Double-reciprocal plot where h = 1 for a MM enzyme Scatchard plot r/[S]h = (1/Kmh)(n-r) where h = 1 for a MM enzyme where h = 1 for a MM enzyme
Rectangular hyperbolic plot (h = Hill coefficient) where h = 1 for a MM enzyme Hill plot Double-reciprocal plot where h = 1 for a MM enzyme Scatchard plot r/[S]h = (1/Kmh)(n-r) where h = 1 for a MM enzyme where h = 1 for a MM enzyme




 Линеаризация уравнения Михаэлиса-Ментен. 3. Преобразование Хейнса-Вольфа
Линеаризация уравнения Михаэлиса-Ментен. 3. Преобразование Хейнса-Вольфа
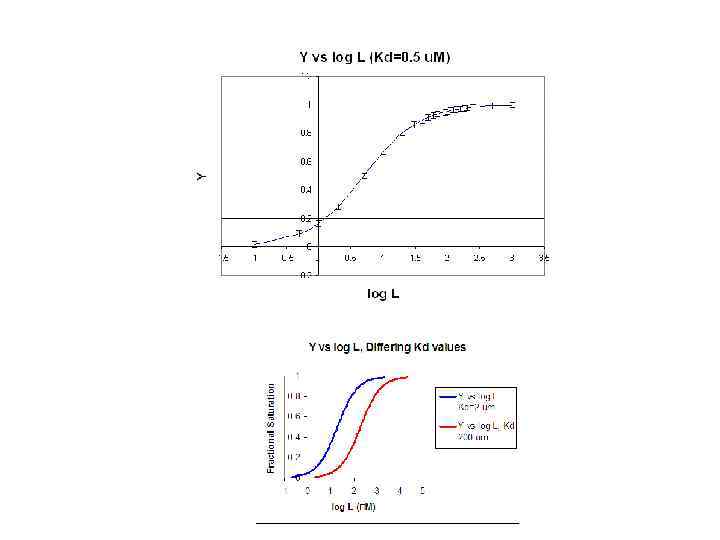
![Y = fractional saturation = Y = ([ML]/[M 0] = [L]/(KD+ [L]) [ML] = Y = fractional saturation = Y = ([ML]/[M 0] = [L]/(KD+ [L]) [ML] =](https://present5.com/presentation/3540715_33786667/image-141.jpg) Y = fractional saturation = Y = ([ML]/[M 0] = [L]/(KD+ [L]) [ML] = [M 0][L]/(KD+ [L]
Y = fractional saturation = Y = ([ML]/[M 0] = [L]/(KD+ [L]) [ML] = [M 0][L]/(KD+ [L]
![[ML] = [M 0][L]/(KD+ [L] Y = fractional saturation = ([ML]/[M 0] = [L]/(KD+ [ML] = [M 0][L]/(KD+ [L] Y = fractional saturation = ([ML]/[M 0] = [L]/(KD+](https://present5.com/presentation/3540715_33786667/image-143.jpg) [ML] = [M 0][L]/(KD+ [L] Y = fractional saturation = ([ML]/[M 0] = [L]/(KD+ [L])
[ML] = [M 0][L]/(KD+ [L] Y = fractional saturation = ([ML]/[M 0] = [L]/(KD+ [L])
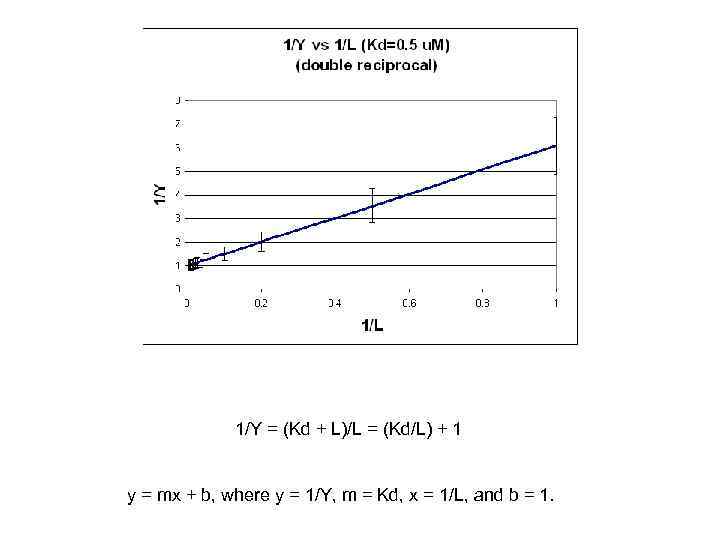 1/Y = (Kd + L)/L = (Kd/L) + 1 y = mx + b, where y = 1/Y, m = Kd, x = 1/L, and b = 1.
1/Y = (Kd + L)/L = (Kd/L) + 1 y = mx + b, where y = 1/Y, m = Kd, x = 1/L, and b = 1.
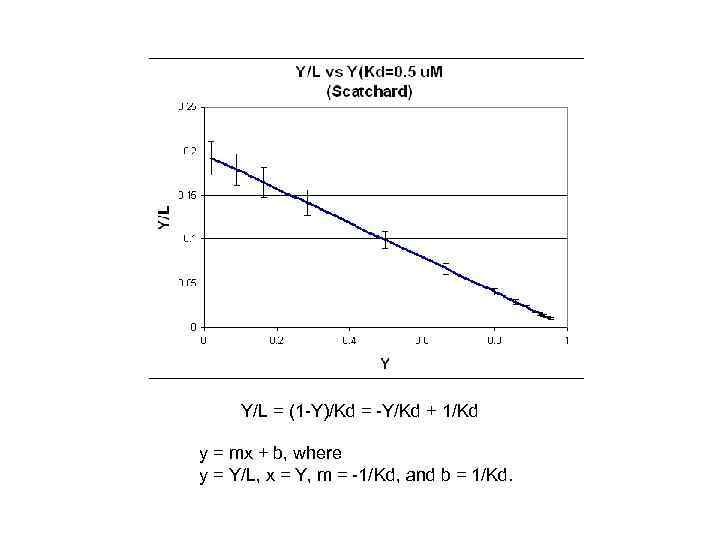 Y/L = (1 -Y)/Kd = -Y/Kd + 1/Kd y = mx + b, where y = Y/L, x = Y, m = -1/Kd, and b = 1/Kd.
Y/L = (1 -Y)/Kd = -Y/Kd + 1/Kd y = mx + b, where y = Y/L, x = Y, m = -1/Kd, and b = 1/Kd.