Феноменология и вероятностные характеристики макросистем Лекция 2 Множество

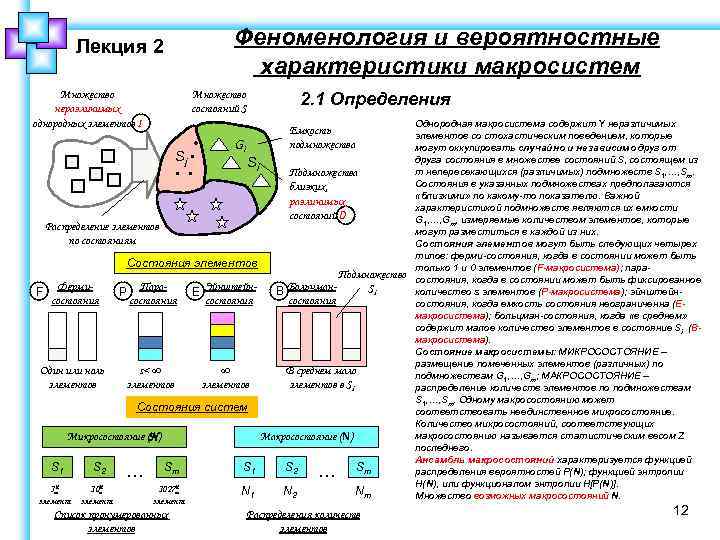Феноменология и вероятностные характеристики макросистем Лекция 2 Множество неразличимых однородных элементов I Множество состояний S • Sj • • • Gi 2. 1 Определения Емкость подмножества Si Распределение элементов по состояниям Подмножества близких, различимых состояний D Состояния элементов F Фермисостояния Один или ноль элементов P Парасостояния E Эйнштейнсостояния s< ∞ элементов B Больцмансостояния Подмножество Si В среднем мало элементов в Si Состояния систем Микросостояние (N) S 1 S 2 3 й 10 й элемент … Макросостояние (N) Sm 1027 й элемент Список пронумерованных элементов S 1 S 2 N 1 N 2 … Sm Nm Распределения количеств элементов Однородная макросистема содержит Y неразличимых элементов со стохастическим поведением, которые могут оккупировать случайно и независимо друг от друга состояния в множестве состояний S, состоящем из m непересекающихся (различимых) подмножеств S 1, …, Sm. Состояния в указанных подмножествах предполагаются «близкими» по какому-то показателю. Важной характеристикой подмножеств являются их емкости G 1, …, Gm, измеряемые количеством элементов, которые могут разместиться в каждой из них. Состояния элементов могут быть следующих четырех типов: ферми-состояния, когда в состоянии может быть только 1 и 0 элементов (F-макросистема); парасостояния, когда в состоянии может быть фиксированное количество s элементов (P-макросистема); эйнштейнсостояния, когда емкость состояния неограниченна (Eмакросистема); больцман-состояния, когда «в среднем» содержит малое количество элементов в состояние Si (Bмакросистема). Состояние макросистемы: МИКРОСОСТОЯНИЕ – размещение помеченных элементов (различных) по подмножествам G 1, …, Gm; МАКРОСОСТОЯНИЕ – распределение количеств элементов по подмножествам S 1, …, Sm. Одному макросостоянию может соответствовать неединственное микросостояние. Количество микросостояний, соответствующих макросостоянию называется статистическим весом Z последнего. Ансамбль макросостояний характеризуется функцией распределения вероятностей P(N); функцией энтропии H(N), или функционалом энтропии Н[P(N)]. Множество возможных макросостояний N. 12

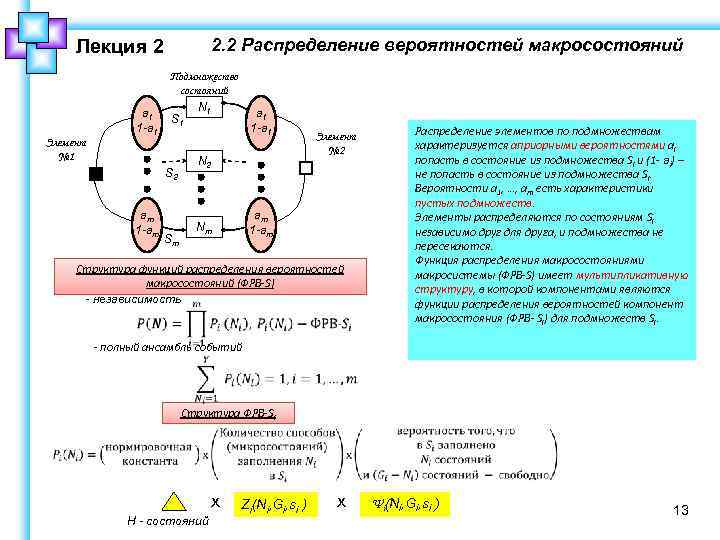2. 2 Распределение вероятностей макросостояний Лекция 2 a 1 1 -a 1 Подмножество состояний N 1 S 1 Элемент № 1 S 2 am 1 -am Sm a 1 1 -a 1 N 2 Элемент № 2 am 1 -am Nm Структура функций распределения вероятностей макросостояний (ФРВ-S) - независимость Распределение элементов по подмножествам характеризуется априорными вероятностями ai попасть в состояние из подмножества Si и (1 - ai) – не попасть в состояние из подмножества Si. Вероятности а 1, …, am есть характеристики пустых подмножеств. Элементы распределяются по состояниям Si независимо друг для друга, и подмножества не пересекаются. Функция распределения макросостояниями макросистемы (ФРВ-S) имеет мультипликативную структуру, в которой компонентами являются функции распределения вероятностей компонент макросостояния (ФРВ- Si) для подмножеств Si. - полный ансамбль событий Структура ФРВ-Si x Н - состояний Zi(Ni, Gi, si ) x Ψi(Ni, Gi, si ) 13

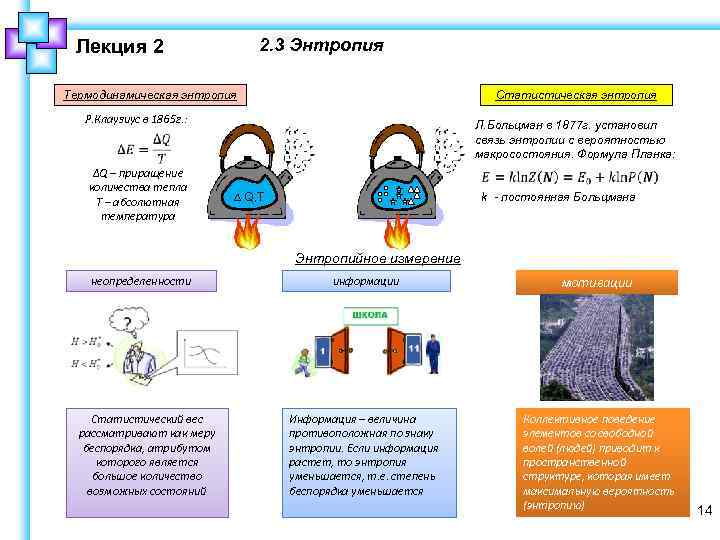2. 3 Энтропия Лекция 2 Термодинамическая энтропия Статистическая энтропия Р. Клаузиус в 1865 г. : ∆Q – приращение количества тепла Т – абсолютная температура Л. Больцман в 1877 г. установил связь энтропии с вероятностью макросостояния. Формула Планка: ∆ Q, T k - постоянная Больцмана Энтропийное измерение неопределенности Статистический вес рассматривают как меру беспорядка, атрибутом которого является большое количество возможных состояний информации мотивации Информация – величина противоположная по знаку энтропии. Если информация растет, то энтропия уменьшается, т. е. степень беспорядка уменьшается Коллективное поведение элементов со свободной волей (людей) приводит к пространственной структуре, которая имеет максимальную вероятность (энтропию) 14

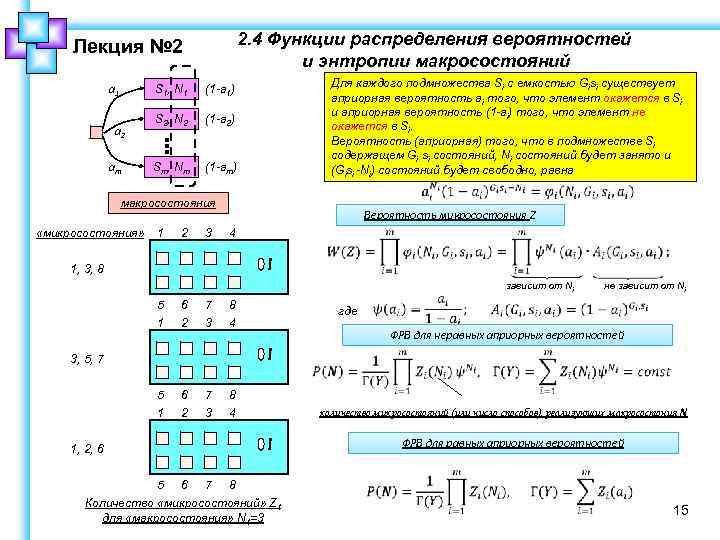2. 4 Функции распределения вероятностей и энтропии макросостояний Лекция № 2 a 1 S 1, N 1 a 2 am (1 -a 1) S 2, N 2 (1 -a 2) Sm , N m (1 -am) Для каждого подмножества Si с емкостью Gisi существует априорная вероятность ai того, что элемент окажется в Si и априорная вероятность (1 -ai) того, что элемент не окажется в Si. Вероятность (априорная) того, что в подмножестве Si содержащем Gi si состояний, Ni состояний будет занято и (Gisi -Ni) состояний будет свободно, равна макросостояния «микросостояния» 1 2 3 Вероятность микросостояния Z 4 1, 3, 8 зависит от Ni 5 1 6 2 7 3 8 4 не зависит от Ni где ФРВ для неравных априорных вероятностей 3, 5, 7 1, 2, 6 5 6 7 8 Количество «микросостояний» Z 1 для «макросостояния» N 1=3 количество микросостояний (или число способов), реализующих макросостония N ФРВ для равных априорных вероятностей 15

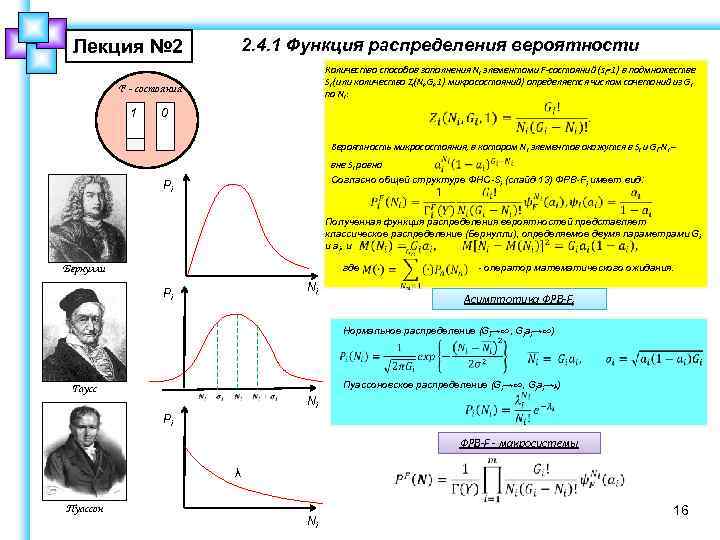Лекция № 2 2. 4. 1 Функция распределения вероятности Количество способов заполнения Ni элементами F-состояний (si=1) в подмножестве Si (или количество Zi(Ni, Gi, 1) микросостояний) определяется числом сочетаний из Gi по Ni: F - состояния 1 0 Вероятность микросостояния, в котором Ni элементов окажутся в Si и Gi-Ni – вне Si равна Согласно общей структуре ФНС-Si (слайд 13) ФРВ-Fi имеет вид: Pi Полученная функция распределения вероятностей представляет классическое распределение (Бернулли), определяемое двумя параметрами Gi и ai, и где Бернулли Ni Pi - оператор математического ожидания. Асимптотика ФРВ-Fi Нормальное распределение (Gi→∞, Giai→∞) Пуассоновское распределение (Gi→∞, Giai→λ) Гаусс Ni Pi ФРВ-F - макросистемы λ Пуассон Ni 16

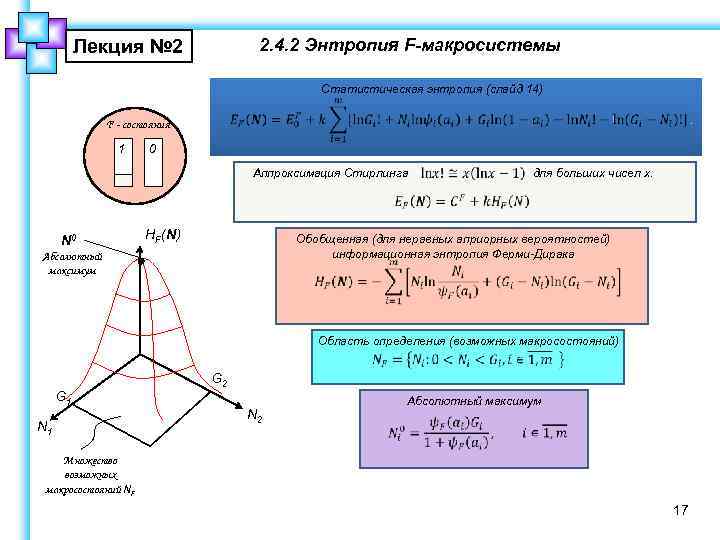2. 4. 2 Энтропия F-макросистемы Лекция № 2 Статистическая энтропия (слайд 14) F - состояния 1 0 Аппроксимация Стирлинга N 0 HF(N) для больших чисел x. Обобщенная (для неравных априорных вероятностей) информационная энтропия Ферми-Дирака Абсолютный максимум Область определения (возможных макросостояний) G 1 N 1 G 2 N 2 Абсолютный максимум Множество возможных макросостояний NF 17

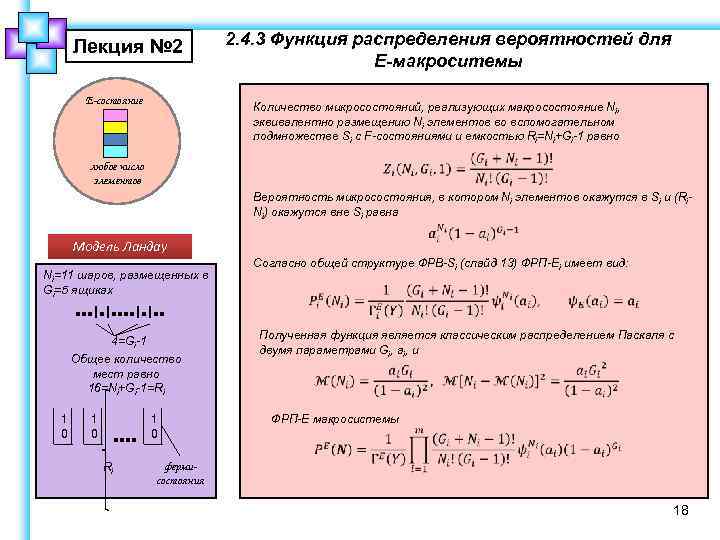Лекция № 2 E-состояние 2. 4. 3 Функция распределения вероятностей для Е-макроситемы Количество микросостояний, реализующих макросостояние Ni, эквивалентно размещению Ni элементов во вспомогательном подмножестве Si с F-состояниями и емкостью Ri=Ni+Gi-1 равно любое число элементов Вероятность микросостояния, в котором Ni элементов окажутся в Si и (Ri. Ni) окажутся вне Si равна Модель Ландау Ni=11 шаров, размещенных в Gi=5 ящиках 4=Gi-1 Общее количество мест равно 16=Ni+Gi-1=Ri 1 0 1 0 Ri Согласно общей структуре ФРВ-Si (слайд 13) ФРП-Еi имеет вид: Полученная функция является классическим распределением Паскаля с двумя параметрами Gi, ai, и ФРП-Е макросистемы фермисостояния 18

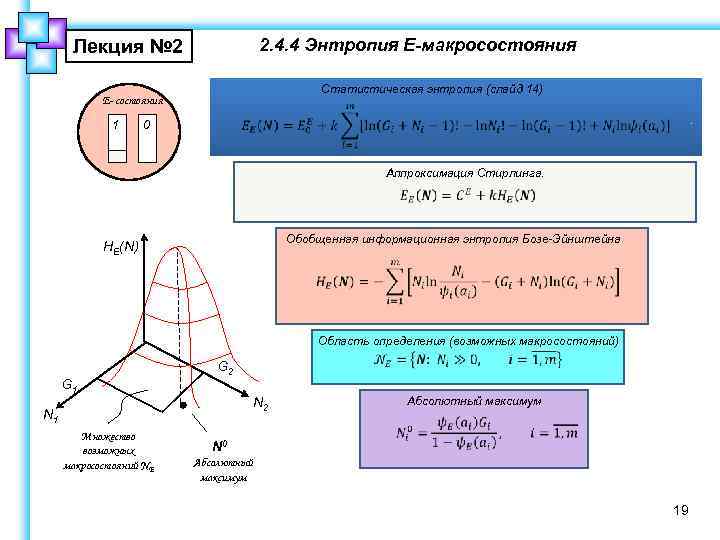2. 4. 4 Энтропия Е-макросостояния Лекция № 2 Статистическая энтропия (слайд 14) E- состояния 1 0 Аппроксимация Стирлинга. Обобщенная информационная энтропия Бозе-Эйнштейна HЕ(N) Область определения (возможных макросостояний) G 1 G 2 N 1 Множество возможных макросостояний NЕ Абсолютный максимум N 0 Абсолютный максимум 19

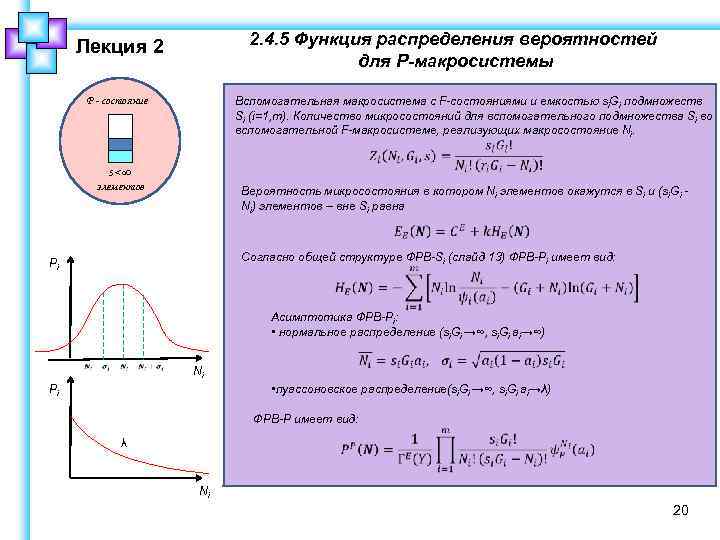2. 4. 5 Функция распределения вероятностей для P-макросистемы Лекция 2 Вспомогательная макросистема с F-состояниями и емкостью si. Gi подмножеств Si (i=1, m). Количество микросостояний для вспомогательного подмножества Si во вспомогательной F-макросистеме, реализующих макросостояние Ni. P - состояние s< ∞ элементов Вероятность микросостояния в котором Ni элементов окажутся в Si и (si. Gi Ni) элементов – вне Si равна Согласно общей структуре ФРВ-Si (слайд 13) ФРВ-Pi имеет вид: Pi Асимптотика ФРВ-Pi: • нормальное распределение (si. Gi →∞, si. Gi ai→∞) Ni • пуассоновское распределение(si. Gi →∞, si. Gi ai→λ) Pi ФРВ-P имеет вид: λ Ni 20

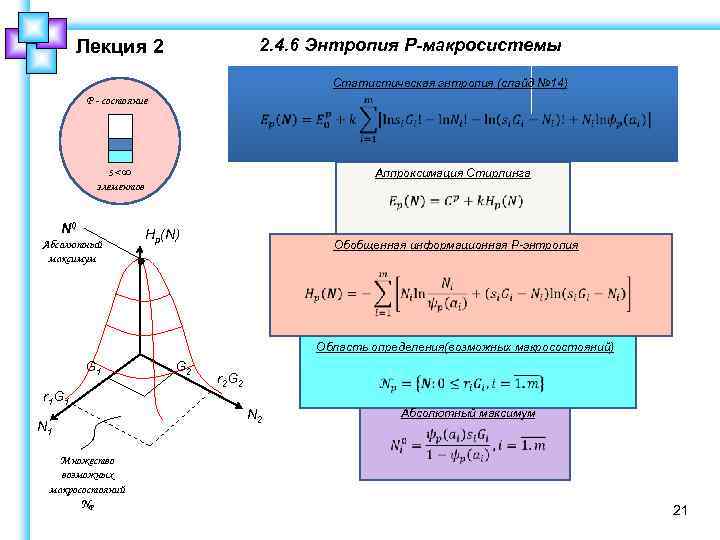2. 4. 6 Энтропия P-макросистемы Лекция 2 Статистическая энтропия (слайд № 14) P - состояние s< ∞ элементов N 0 Абсолютный максимум Аппроксимация Стирлинга Hp(N) Обобщенная информационная Р-энтропия Область определения(возможных макросостояний) G 1 r 1 G 1 N 1 Множество возможных макросостояний NP G 2 r 2 G 2 N 2 Абсолютный максимум 21

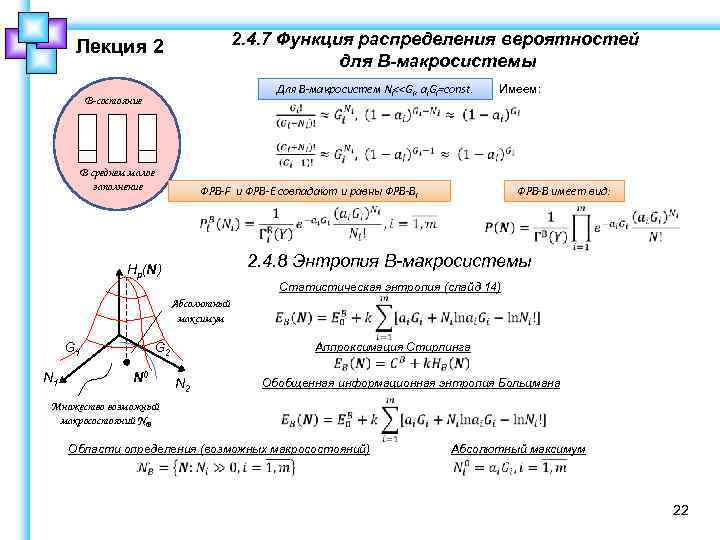2. 4. 7 Функция распределения вероятностей для В-макросистемы Лекция 2 Для В-макросистем Ni<