920a6c13fa0c17f12a56ea3e5acfc3e6.ppt
- Количество слайдов: 36

Feedback Control and Multi-Agent Systems: Ubiquitous and Increasingly Interdependent Prof. Bill Dunbar Autonomous Systems Group Computer Engineering

What are Systems? … ANYTHING in Engineering, usually with Dynamics. Some familiar examples: How do we describe systems? … with math!

Math: Describing Diverse Engineering Systems in a Common Way Internet backbone CA power grid In these Examples: San Fran ATC

Control Systems are Hidden Engineering Systems “A Control System is a device in which a sensed quantity is used to modify the behavior of a system through computation and actuation. ”

• My (and Potentially Your) Research Robotics – Exploration – Toys – Competition (soccer) • Automated Freeways • Supply Chain Management

Eventually…A Fully Autonomous Vehicle Off-Road Dessert Race

The Potential is Enormous • Researchers at Caltech are working toward the math model of the “fruit fly system, ” with the ultimate objective of making a micromechanical fly!

Distributed Optimization-Based Control of Multiagent Systems Ass. Prof. Bill Dunbar Autonomous Systems Group Computer Engineering
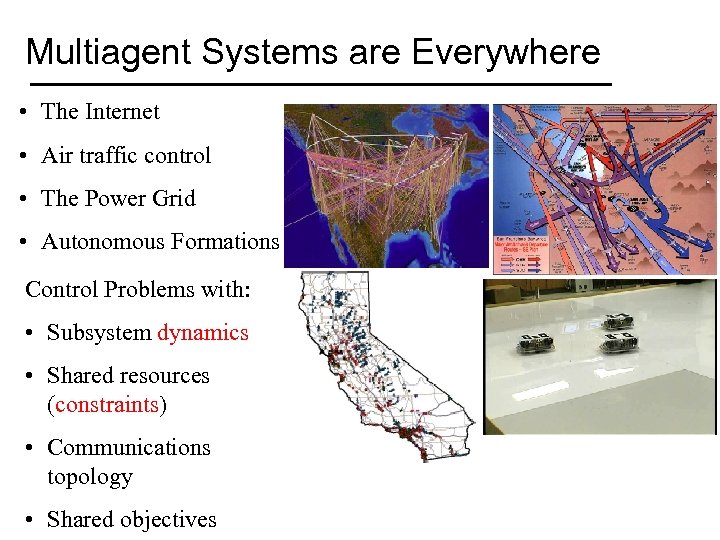
Multiagent Systems are Everywhere • The Internet • Air traffic control • The Power Grid • Autonomous Formations Control Problems with: • Subsystem dynamics • Shared resources (constraints) • Communications topology • Shared objectives
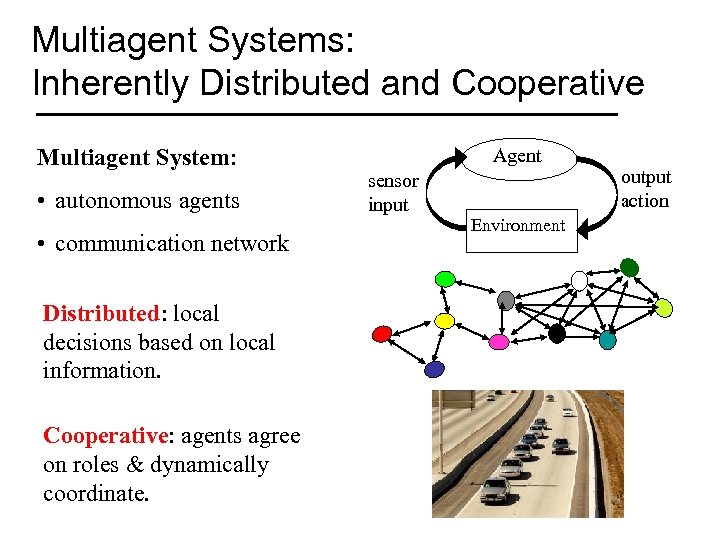
Multiagent Systems: Inherently Distributed and Cooperative Multiagent System: • autonomous agents • communication network Distributed: local decisions based on local information. Cooperative: agents agree on roles & dynamically coordinate. Agent sensor input Environment output action
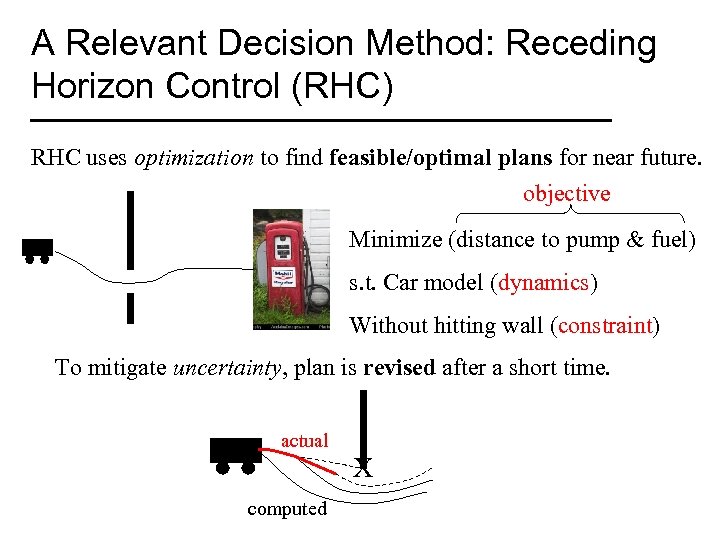
A Relevant Decision Method: Receding Horizon Control (RHC) RHC uses optimization to find feasible/optimal plans for near future. objective Minimize (distance to pump & fuel) s. t. Car model (dynamics) Without hitting wall (constraint) To mitigate uncertainty, plan is revised after a short time. actual X computed

Mathematics of RHC is Finite Horizon Optimal Control objective Minimize (distance to pump& fuel) s. t. Car dynamics Without hitting wall (constraint)

Convergence of RHC Requires Appropriate Planning Horizon and Terminal Penalty Theoretical conditions sufficient & in absence of explicit uncertainty. *[Mayne et al. , 2000]
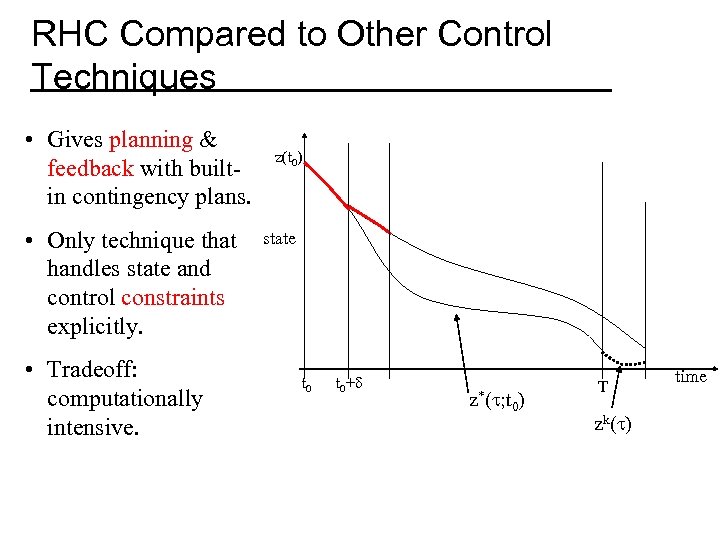
RHC Compared to Other Control Techniques • Gives planning & feedback with builtin contingency plans. • Only technique that handles state and control constraints explicitly. • Tradeoff: computationally intensive. z(t 0) state t 0+d z*(t; t 0) T zk(t) time

RHC Successful in Applications: Process to Flight Control Caltech flight control experiment: Tracking ramp input of 16 meters in horizontal, step input of 1 m in altitude. RHC updates at 10 Hz, trajectories generated by NTG software package. Movie
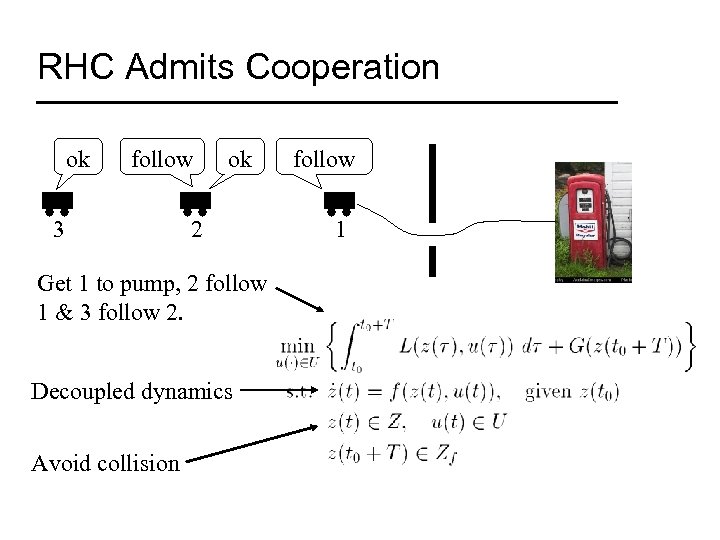
RHC Admits Cooperation ok follow 3 ok 2 Get 1 to pump, 2 follow 1 & 3 follow 2. Decoupled dynamics Avoid collision follow 1
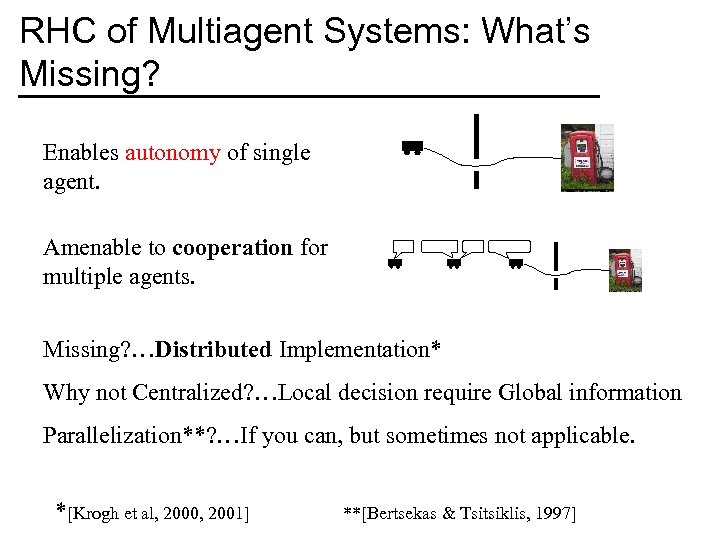
RHC of Multiagent Systems: What’s Missing? Enables autonomy of single agent. Amenable to cooperation for multiple agents. Missing? …Distributed Implementation* Why not Centralized? …Local decision require Global information Parallelization**? …If you can, but sometimes not applicable. *[Krogh et al, 2000, 2001] **[Bertsekas & Tsitsiklis, 1997]

My Contribution: A Distributed Implementation of RHC Distributed: local decisions based on local information. Decoupled subsystem dynamics/constraints, Coupled cost L Decomposition

Solution of Sub-problems requires Assumed Plan for Neighbors Agent 3 z 3(t 0) What 3 does state What 2 assumes t 0+d z 3*(t; t 0) z 3 k(t) time
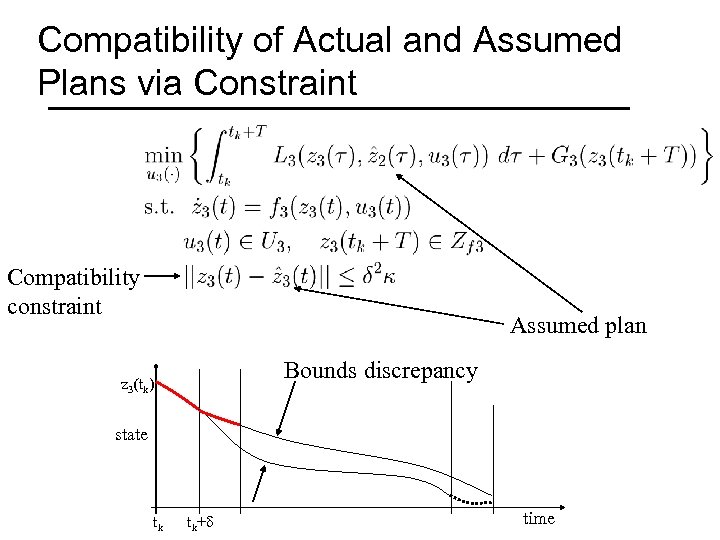
Compatibility of Actual and Assumed Plans via Constraint Compatibility constraint Assumed plan Bounds discrepancy z 3(tk) state tk tk+d time

Distributed Implementation Requires Synchrony & Common Horizon T

Conditions for Theory are General

Convergence Conditions: Same as Centralized plus Bound on Update Period *[Dunbar & Murray, Accepted to Automatica, June, 2004]
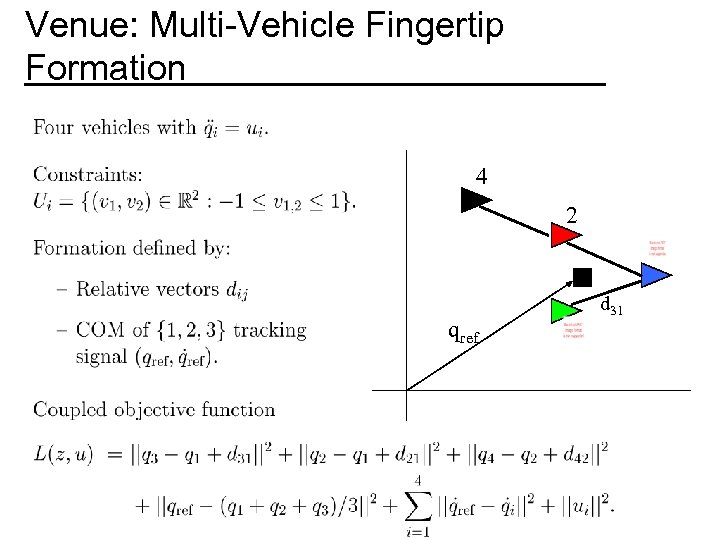
Venue: Multi-Vehicle Fingertip Formation 4 2 qref d 31

Decomposition of Coupled Cost
Simulation Parameters 4 2 : Reference signal : Actual COM of {1, 2, 3}

Centralized RHC: Benchmark for Comparison
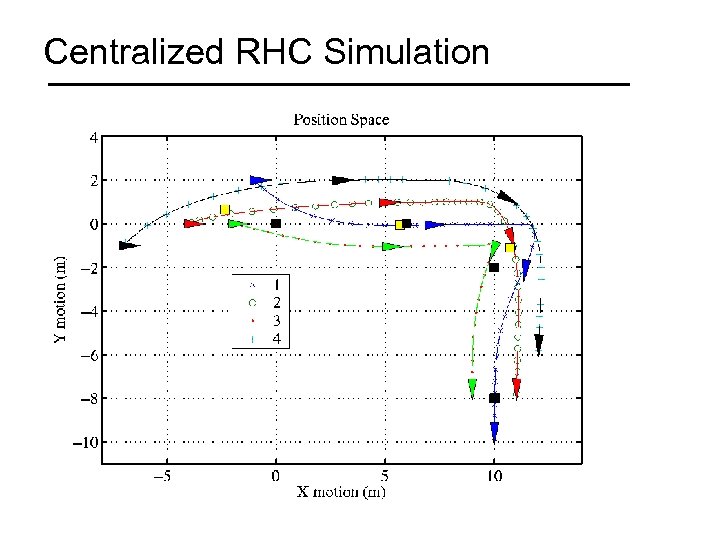
Centralized RHC Simulation

Distributed RHC is Comparable to Centralized RHC
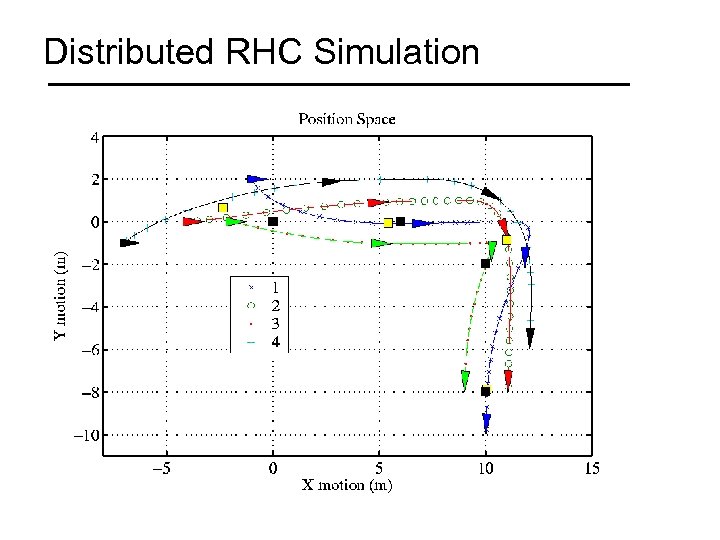
Distributed RHC Simulation

Naïve Approach Produces Less Desirable Performance
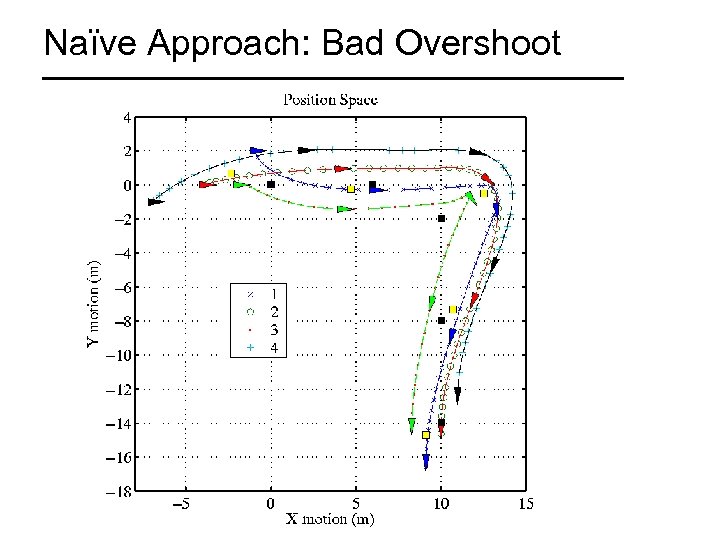
Naïve Approach: Bad Overshoot

Summary of Contribution Distributed implementation of RHC is provable convergent, performs well, and is applicable to a class of Multiagent Systems: • Distributed & cooperative structure: § § Decomposition and incorporation of compatibility constraint § • Local decisions based on local information Coordination via sharing feasible plans Applicable for: § Heterogeneous nonlinear dynamics § Generic objective function (need not be quadratic) § Coupling constraints

Conclusions • Theory conservative; useful as guideline for implementation. • Scalable: computational complexity independent of Na ; communication complexity independent of Na but dependent on Ni (size of neighborhood). • Communicating trajectories: more intensive than traditional decentralized control, but not too bad, given smoothness properties. • Less communication than required by parallelization. Tradeoff: not recovering centralized solution to original problem, but that of a modified problem.

Current and Ongoing Work Theoretically: • Locally synchronous and asynchronous versions • DONE: Coupled subsystem dynamics. Potential applications: § Process control § Supply chain management • Reduced order contingency plans • Connection with rollout algorithms in MDPs

Current and Ongoing Work Applications: • Coordinated UAVs • Mobile Sensor Networks § Robots coordinating for toxin detection • Intelligent Transportation Systems § Automated freeways § Semi-automated Air Traffic Control • Interdisciplinary examples: § Supply chain management (Business) § Power/Water resource management
920a6c13fa0c17f12a56ea3e5acfc3e6.ppt