6ff54411138ec910593be956d6016a5e.ppt
- Количество слайдов: 19

Feb. 23 Statistic for the day: Estimated market value of usable body parts of an adult human: $46, 000 Source: Harper’s index Assignment: Read Chapter 15 pp. 264 -271 Exercises pp. 275 -276: 19, 21, 22, 25 These slides were created by Tom Hettmansperger and in some cases modified by David Hunter
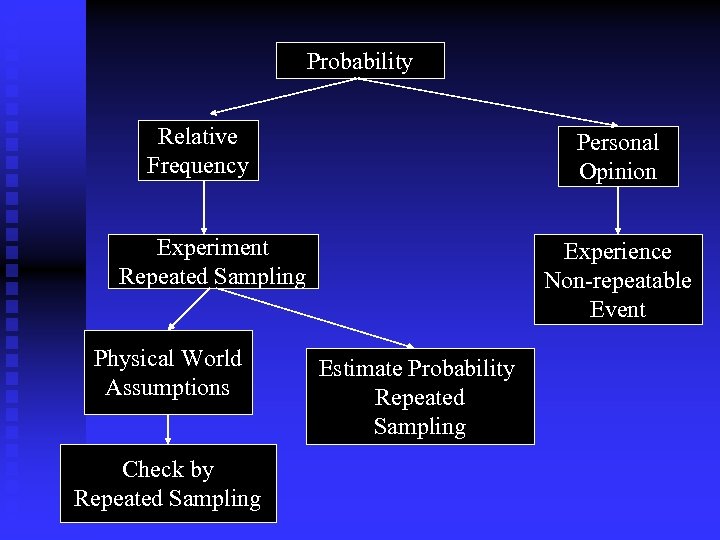
Probability Relative Frequency Personal Opinion Experiment Repeated Sampling Physical World Assumptions Check by Repeated Sampling Experience Non-repeatable Event Estimate Probability Repeated Sampling

Example 1 Relative frequency Repeated sampling Physical world assumption • coin • dice • cards 0 4 Roll this strange die. What is the probability of 4? What is the physical world assumption? Pr(get a 4) = 4/6 = 2/3 0 4 4 4

Example 2 Relative frequency Repeated sampling Estimate probability by repeated sampling Tack What is the probability of landing point up?

Example 3 Personal probability Opinion, experience Non-repeatable event A in Stat 100
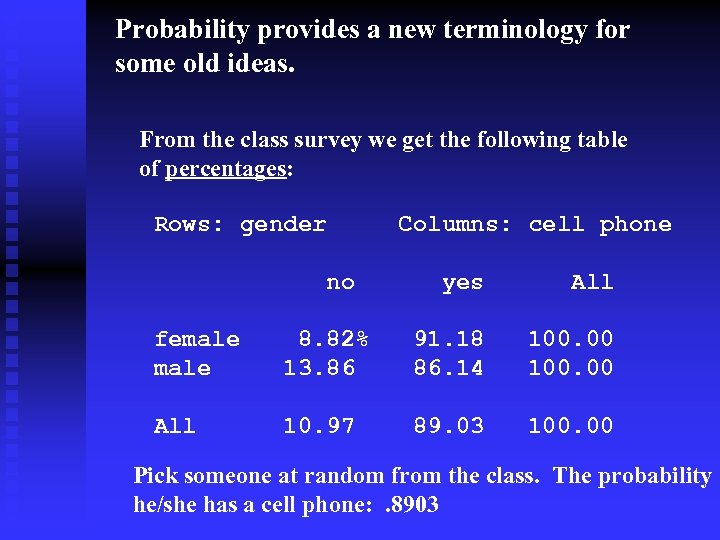
Probability provides a new terminology for some old ideas. From the class survey we get the following table of percentages: Rows: gender Columns: cell phone no yes All female 8. 82% 13. 86 91. 18 86. 14 100. 00 All 10. 97 89. 03 100. 00 Pick someone at random from the class. The probability he/she has a cell phone: . 8903

Rules: For combining probabilities 0 < Probability < 1 1. If there are only two possible outcomes, then their probabilities must sum to 1. 2. If two events cannot happen at the same time, they are called mutually exclusive. The probability of at least one happening (one or the other) is the sum of their probabilities. [1. is a special case of this. ] 3. If two events do not influence each other, they are called independent. The probability that they happen at the same time is the product of their probabilities. 4. If the occurrence of one event forces the occurrence of another event, then the probability of the second event is always at least as large as the probability of the first event.

1. If there are only two possible outcomes, then their probabilities must sum to 1. Rows: gender Columns: cell phone no yes All female 12 14 136 101 All 26 237 Pr(no) = 26/237 =. 11 Relative frequency. Pr(yes) = 1 – Pr (no) = 1 -. 11 =. 89

Example 3 p 261: (relative frequency) Pr(lost luggage) = 1/176 =. 00568 Then Pr(not lost) = 1 – 1/176 = 175/176 =. 99432 The point: Pr(lost) + Pr(not lost) = 1 So if we know Pr(lost), then Pr(not lost) = 1 – Pr(lost).

2. If two events cannot happen at the same time, they are called mutually exclusive. The probability of at least one happening (one or the other) is the sum of their probabilities. [1. is a special case of this. ] Example 5 p 262: (personal probability) Suppose Pr(A in stat) =. 50 and Pr( B in stat) =. 30, Then Pr( A or B in stat) =. 50 +. 30 =. 80 Note the events ‘A in stat’ and ‘B in stat’ are mutually exclusive.

Rows: gender Columns: cell phone no yes All female 12 14 124 87 136 101 All 26 211 237 Pr( female with cell phone) = 124/237 =. 523 Pr(male without cell phone) = 14/237 =. 059 Mutually exclusive events Pr( female w. cell p or male w/o cell p) =. 523 +. 059 =. 582 Relative frequency.

Rows: gender Columns: cell phone no yes All female 12 14 124 87 136 101 All 26 211 237 Pr(female) = 136/237 =. 574 Pr(male) =. 426 Pr(cell phone) = 211/237 =. 890 Pr(no cell phone) =. 110 Pr(female or cell phone) = ? Note it cannot be. 574 +. 890 = 1. 464 Why not? Pr(male or no cell phone) = ? Can it be. 426 +. 110 =. 536?

3. If two events do not influence each other, they are called independent. The probability that they happen at the same time is the product of their probabilities. Example 8 p 263 (personal probability) Suppose you believe: Pr(A in stat) =. 5 and Pr(A in history) =. 6 Further you believe that the two events are independent. So that they do not influence each other. Then Pr(A in stat and A in hist) = (. 5)x(. 6) =. 30

Example (personal probability) You believe: Pr(own a house in 10 years) =. 70 Pr(live in Pa in 10 years) =. 40 You also believe they are independent events. Then Pr( you will own a house and live in Pa) =. 7 x. 4 =. 28 -----------------------------------Suppose you also believe Pr(you will live in a city in 10 years) =. 60 Pr(you will own a house and live in a city) = ? May not be independent events.

Suppose you also believe Pr(you will live in a city in 10 years) =. 60 Pr(you will own a house and live in a city) = ? May not be independent events. ------------------------------A TEST FOR INDEPENDENCE OF EVENTS: Ask if the probability of owning a house changes when you learn that you will be living in a city. Pr(own house) =. 70 Pr(own house given you live in a city) may be less than. 70. This means the events are dependent.
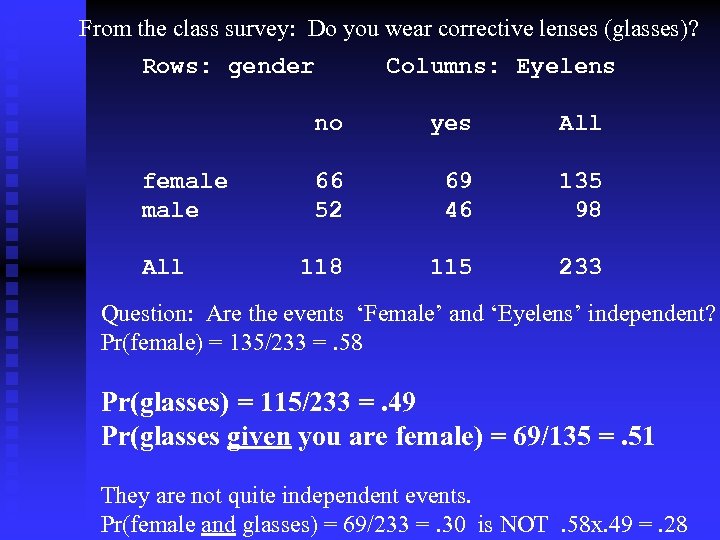
From the class survey: Do you wear corrective lenses (glasses)? Rows: gender Columns: Eyelens no female All yes All 66 52 69 46 135 98 115 233 Question: Are the events ‘Female’ and ‘Eyelens’ independent? Pr(female) = 135/233 =. 58 Pr(glasses) = 115/233 =. 49 Pr(glasses given you are female) = 69/135 =. 51 They are not quite independent events. Pr(female and glasses) = 69/233 =. 30 is NOT. 58 x. 49 =. 28
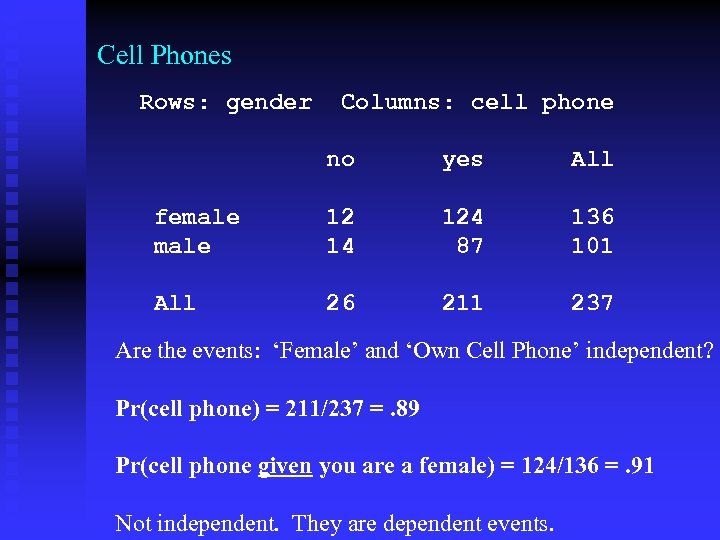
Cell Phones Rows: gender Columns: cell phone no yes All female 12 14 124 87 136 101 All 26 211 237 Are the events: ‘Female’ and ‘Own Cell Phone’ independent? Pr(cell phone) = 211/237 =. 89 Pr(cell phone given you are a female) = 124/136 =. 91 Not independent. They are dependent events.

4. If the occurrence of one event forces the occurrence of another event, then the probability of the second event is always at least as large as the probability of the first event. If event A forces B to occur, then Pr(A) < P(B)

Tattoos and Pierces Rows: tattoo Columns: body no yes All no yes 157 23 32 22 189 45 All 180 54 234 The event ‘have a tattoo and have body pierce’ forces the event ‘have a tattoo’ to occur. Hence Pr(tattoo and pierce) < Pr(tattoo) We can see it in the table: Pr(tattoo and pierce) = 22/234 =. 094 but Pr(tattoo) = 54/234 =. 231. And. 094 <. 231.
6ff54411138ec910593be956d6016a5e.ppt