Feature Selection as Relevant Information Encoding Naftali Tishby School of Computer Science and Engineering The Hebrew University, Jerusalem, Israel NIPS 2001
Many thanks to: Noam Slonim Amir Globerson Bill Bialek Fernando Pereira Nir Friedman
Feature Selection? • NOT generative modeling! – no assumptions about the source of the data • Extracting relevant structure from data – functions of the data (statistics) that preserve information • Information about what? • Approximate Sufficient Statistics • Need a principle that is both general and precise. – Good Principles survive longer!
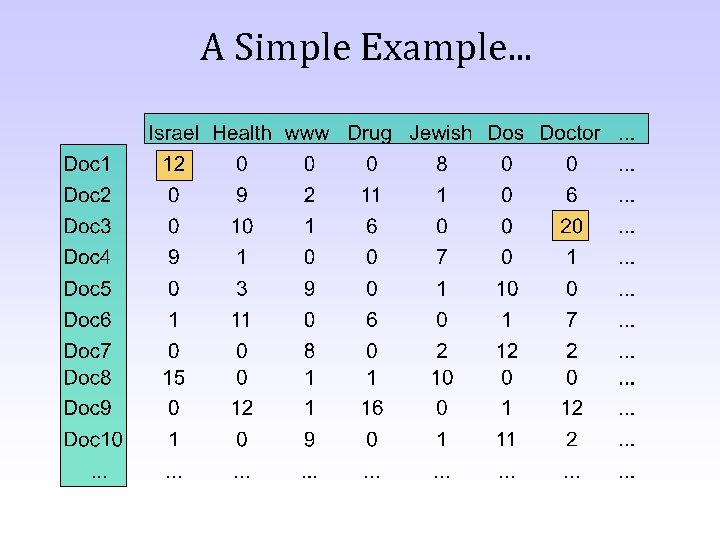
A Simple Example. . .
Simple Example
A new compact representation The document clusters preserve the relevant information between the documents and words
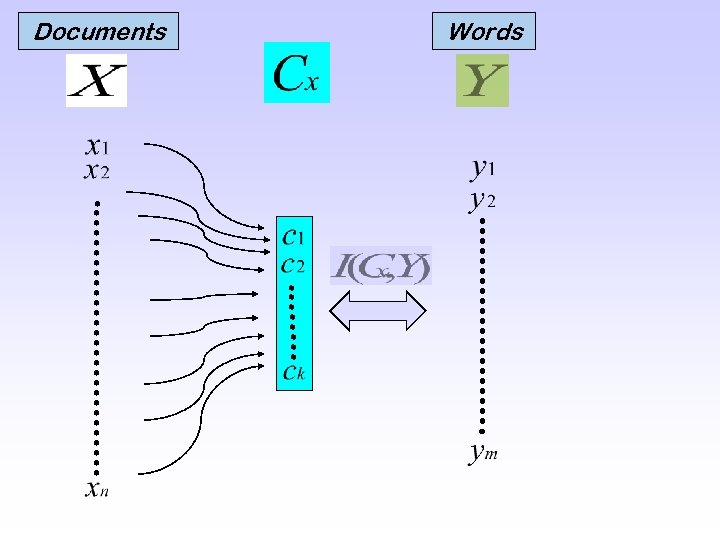
Documents Words
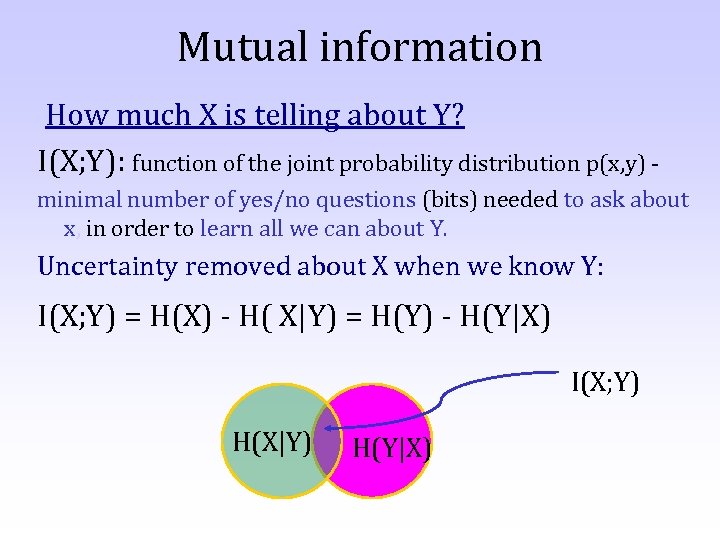
Mutual information How much X is telling about Y? I(X; Y): function of the joint probability distribution p(x, y) minimal number of yes/no questions (bits) needed to ask about x, in order to learn all we can about Y. Uncertainty removed about X when we know Y: I(X; Y) = H(X) - H( X|Y) = H(Y) - H(Y|X) I(X; Y) H(X|Y) H(Y|X)
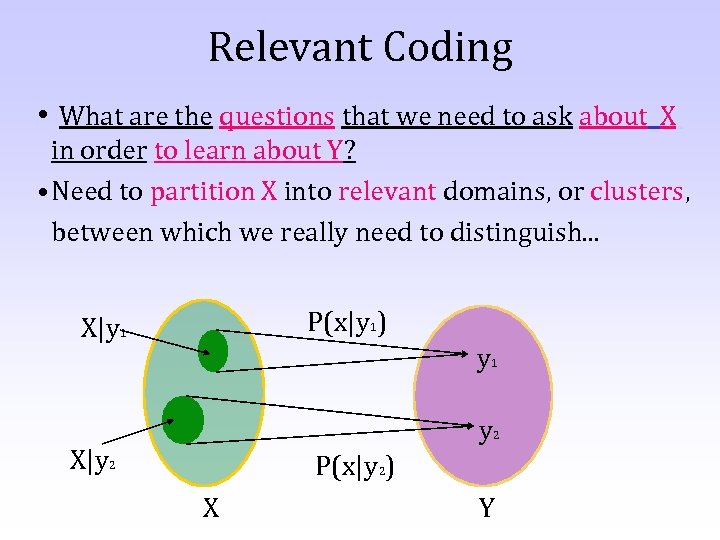
Relevant Coding • What are the questions that we need to ask about X in order to learn about Y? • Need to partition X into relevant domains, or clusters, between which we really need to distinguish. . . P(x|y 1) X|y 1 y 2 X|y 2 P(x|y 2) X Y
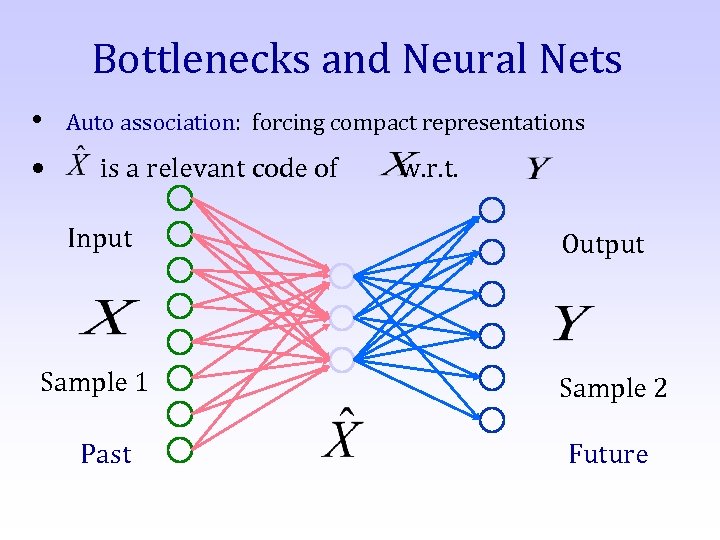
Bottlenecks and Neural Nets • • Auto association: forcing compact representations is a relevant code of Input Sample 1 Past w. r. t. Output Sample 2 Future
• Q: How many bits are needed to determine the relevant representation? – need to index the max number of non-overlapping green blobs inside the blue blob: (mutual information!)
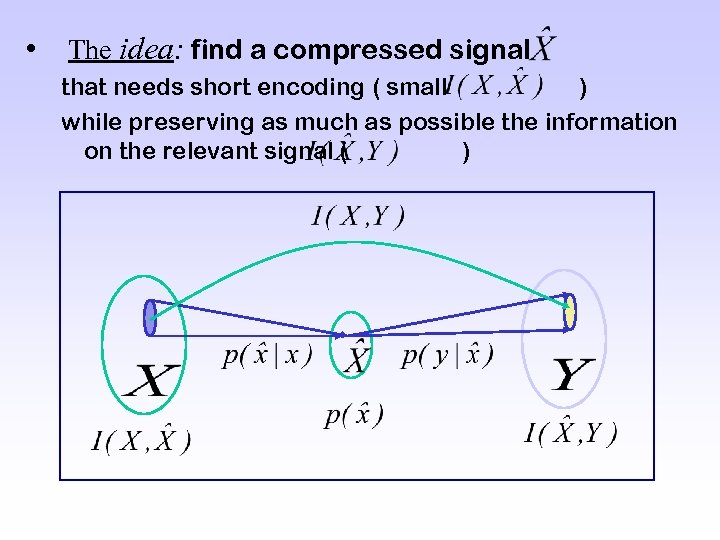
• The idea: find a compressed signal that needs short encoding ( small ) while preserving as much as possible the information on the relevant signal ( )
A Variational Principle We want a short representation of X that keeps the information about another variable, Y, if possible.
The Self Consistent Equations • Marginal: • Markov condition: • Bayes’ rule:
The emerged effective distortion measure: • Regular if • Small if is absolutely continuous w. r. t. predicts y as well as x:
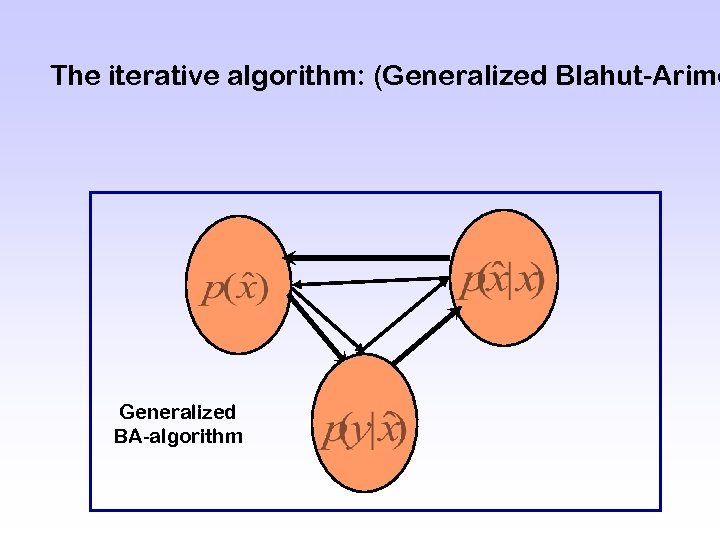
The iterative algorithm: (Generalized Blahut-Arimo Generalized BA-algorithm
The Information Bottleneck Algorithm “free energy”
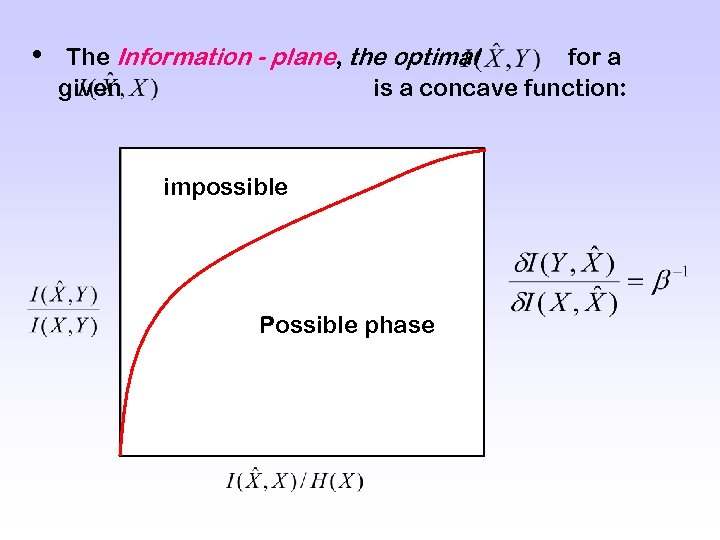
• The Information - plane, the optimal for a given is a concave function: impossible Possible phase
Manifold of relevance The self consistent equations: Assuming a continuous manifold for Coupled (local in ) eigenfunction equations, with as an eigenvalue.
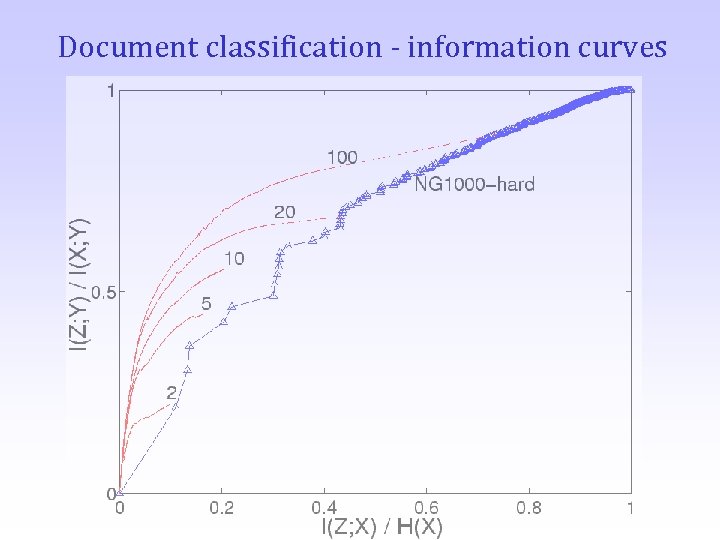
Document classification - information curves
Multivariate Information Bottleneck • Complex relationship between many variables • Multiple unrelated dimensionality reduction schemes • Trade between known and desired dependencies • Express IB in the language of Graphical Models • Multivariate extension of Rate-Distortion Theory
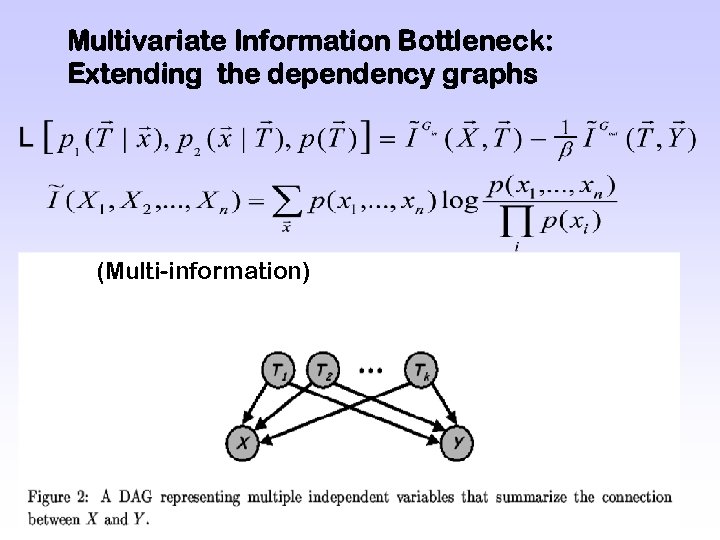
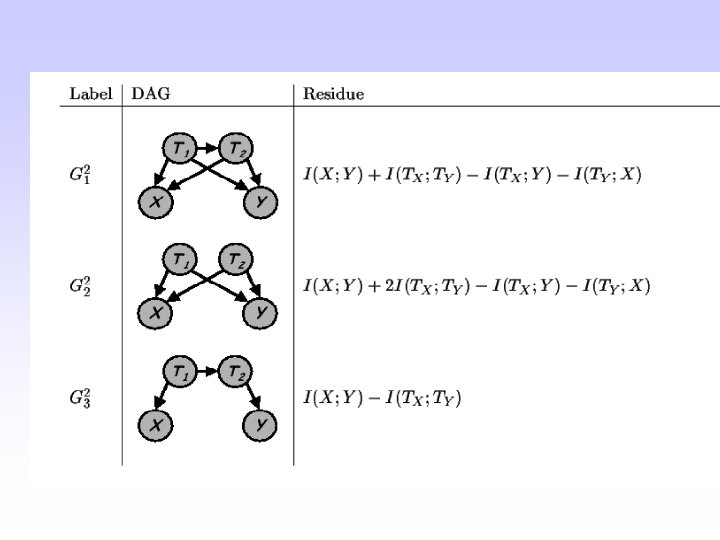
Multivariate Information Bottleneck: Extending the dependency graphs (Multi-information)
Sufficient Dimensionality Reduction (with Amir Globerson) • Exponential families have sufficient statistics • Given a joint distribution the exponential form: , find an approximation of This can be done by alternating maximization of Entropy under the constraints: The resulting functions are our relevant features at rank d.
Summary • We present a general information theoretic approach for extracting relevant information. • It is a natural generalization of Rate-Distortion theory with similar convergence and optimality proofs. • Unifies learning, feature extraction, filtering, and prediction. . . • Applications (so far) include: – Word sense disambiguation – – Document classification and categorization Spectral analysis Neural codes Bioinformatics, … – Data clustering based on multi-distance distributions –…
Скачать презентацию Feature Selection as Relevant Information Encoding Naftali Tishby
bc88a996a5ae1af4b5965c9db7acfd6e.ppt