FE Exam Review Electrical Circuits The FE exam

FE Exam Review Electrical Circuits The FE exam consists of 180 multiple-choice questions. During the morning session, all examinees take a general exam common to all disciplines. During the afternoon session, examinees can opt to take a general exam or a discipline-specific (chemical, civil, electrical, environmental, industrial, or mechanical) exam. See exam specifications for more details.

• XI. Electricity and Magnetism 9% • A. Charge, energy, current, voltage, power • B. Work done in moving a charge in an electric field (relationship between voltage and work) • C. Force between charges • D. Current and voltage laws (Kirchhoff, Ohm) • E. Equivalent circuits (series, parallel) • F. Capacitance and inductance • G. Reactance and impedance, and admittance • H. AC circuits • I. Basic complex algebra

Exam Strategies • Only 4 minutes per problem. –Don’t dwell on a problem. • Do the ones you know. Make an “educated guess” at the ones you don’t know. • Answers are typically in SI unit. Set your calculator to engineering notation. • Pay attention to units (degrees vs. radians)

FE supplies equations You can visit their page To get one http: //www. ncees. org/exams/study%5 Fmaterial s/fe%5 Fhandbook/

Electric Field Electric field due to single charge: E = k k=8. 89 x 109 Nm 2/C 2 Uniform electric field due to uniform distribution of surface charge: Electric potential due to single charge Potential difference in uniform electric field: ΔV = E●d Potential energy : ΔU = qΔV Charge in uniform electric field qΔV= Kf -Ki F =q. E = ma

Capacitance C = Q/ΔV, unit: farad [F] C =εo. A /d, with dielectric C=keo. A/d Cseries = (1/C 1+1/C 2 + … + 1/Cn)-1 Cparallel = C 1 + C 2 + …. + Cn U = ½CV 2 εo =8. 85 x 10 -12 C 2/Nm 2

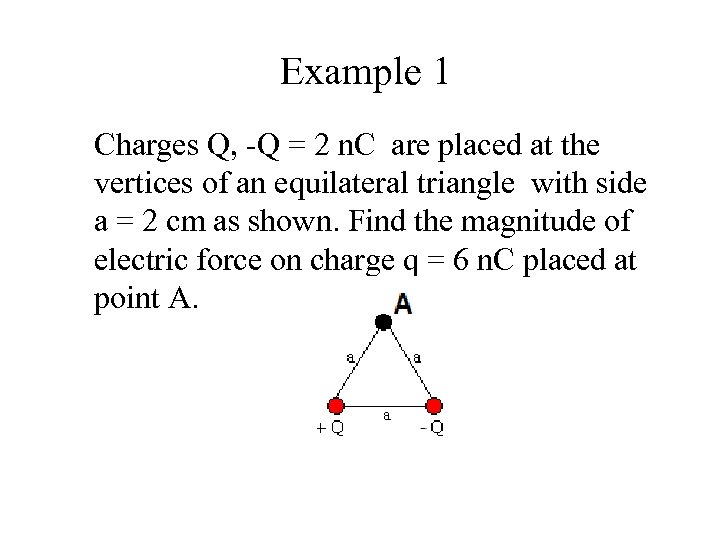Example 1 Charges Q, -Q = 2 n. C are placed at the vertices of an equilateral triangle with side a = 2 cm as shown. Find the magnitude of electric force on charge q = 6 n. C placed at point A.

Example 2, 3 2. An electron with a speed of 5 x 106 m/s i enters an uniform electric field E =1000 N/C i. a. How long will it take for the electron to come to stop? qe = 1. 6 x 10 -19 C me = 9. 11 x 10 -31 kg 3. Find the potential difference needed for the electron to obtain a speed of 3 x 107 m/s.

Example 4 Determine the charge on capacitor C 1 when C 1=10 µF, C 2=12 µF, C 3= 15 µF, Ceq= 4μF and V 0=7 V. (Hint: If capacitors are connected in series, then charge on each capacitor is the same as that on equivalent capacitor a. 0. 5 x 10 -5 C b. 2. 8 x 10 -5 C c. 5. 2 x 10 -5 C d. 7. 0 x 10 -5 C e. 1. 1 x 10 -4 C

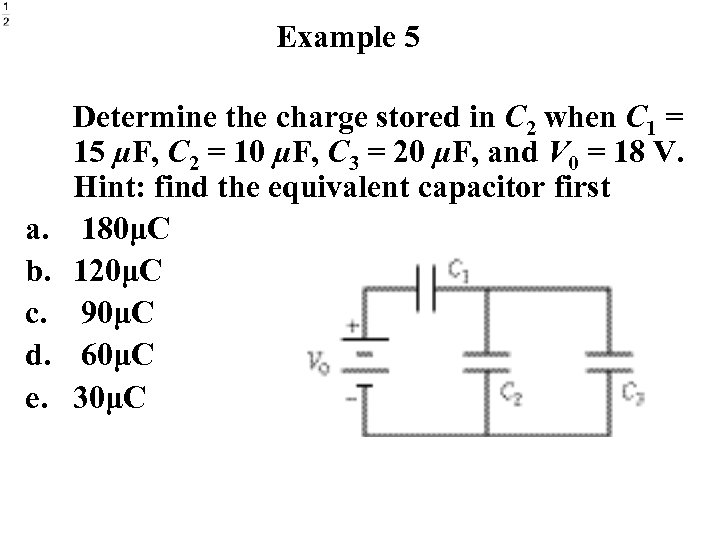Example 5 a. b. c. d. e. Determine the charge stored in C 2 when C 1 = 15 µF, C 2 = 10 µF, C 3 = 20 µF, and V 0 = 18 V. Hint: find the equivalent capacitor first 180μC 120μC 90μC 60μC 30μC

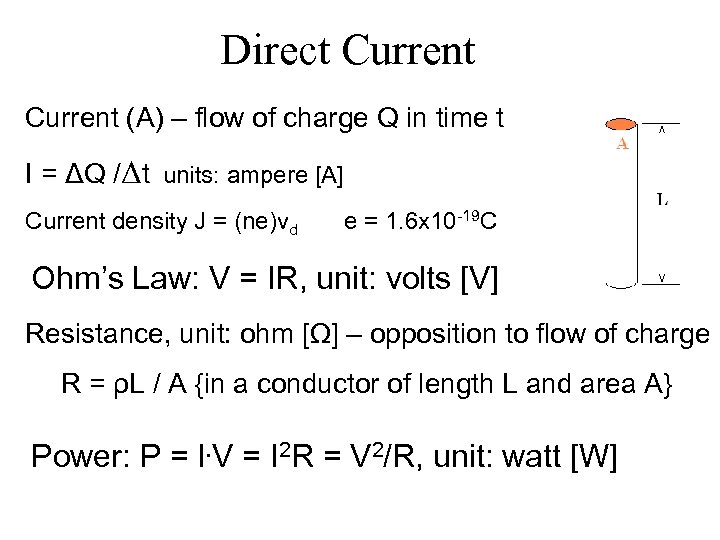Direct Current (A) – flow of charge Q in time t I = ΔQ /Δt units: ampere [A] Current density J = (ne)vd e = 1. 6 x 10 -19 C Ohm’s Law: V = IR, unit: volts [V] Resistance, unit: ohm [Ω] – opposition to flow of charge R = ρL / A {in a conductor of length L and area A} Power: P = I. V = I 2 R = V 2/R, unit: watt [W]

Combination of Resistors Rseries = R 1 + R 2 + …. + Rn Rparallel = (1/R 1 + 1/R 2 + … + 1/Rn)-1

A wire carries a steady current of 0. 1 A over a period of 20 s. What total charge passes through the wire in this time interval? a. 200 C I=Q/t 1 A=1 C/1 s b. 20 C c. 2 C Q = It Q = 0. 1 A*20 s = 2 C d. 0. 005 C

A metallic conductor has a resistivity of 18 10 6 m. What is the resistance of a piece that is 30 m long and has a uniform cross sectional area of 3. 0 mm 2? Resistivity a. 0. 056 b. 180 R=r*L/A c. 160 Resistance R=18*10 -6 Ωm*30 m / d. 90 3*10 -6 m 2 R = 180

A 60 -W light bulb is in a socket supplied with 120 V. What is the current in the bulb? a. 0. 50 A b. 2. 0 A P = V*I = V 2/R = I 2*R c. 60 A d. 7 200 A 60 = 120*I >> I = 60/120 = 0. 5

If a lamp has resistance of 120 when it operates at 100 W, what is the applied voltage? a. 110 V b. 120 V P = V*I = V 2/R = I 2*R c. 125 V d. 220 V 100 = V 2 /120 V = sqrt(120*100) = 11*10 = 110

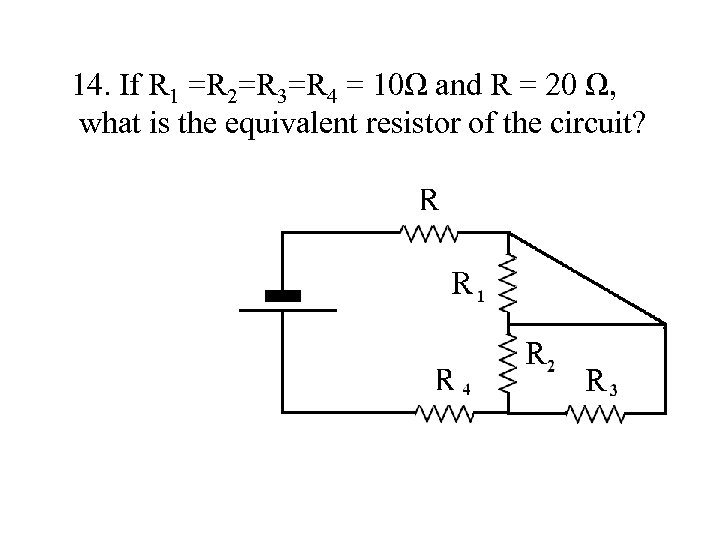14. If R 1 =R 2=R 3=R 4 = 10Ω and R = 20 Ω, what is the equivalent resistor of the circuit?

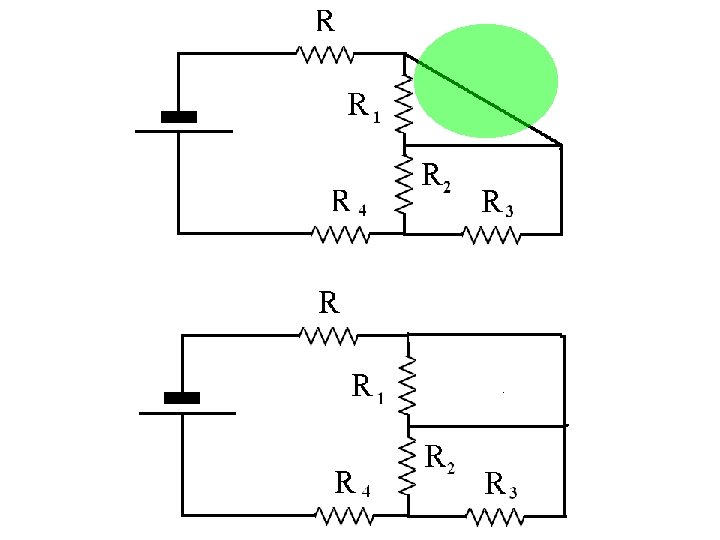
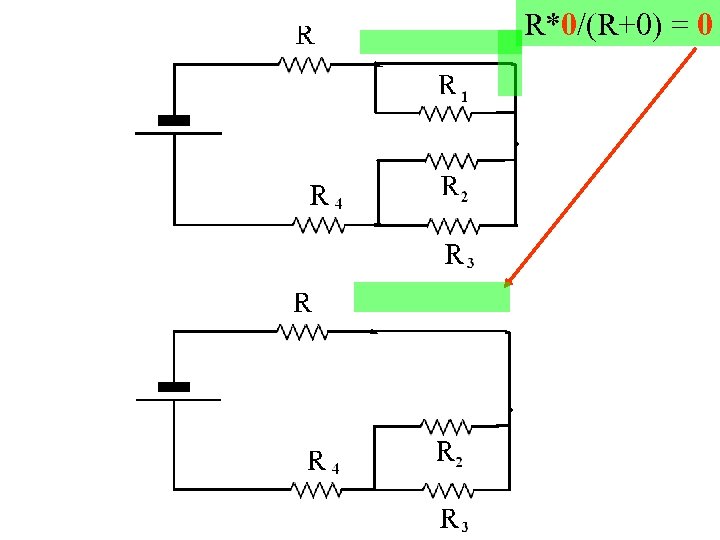R*0/(R+0) = 0

Example 14 cd • Req =(1/R 2+ 1/R 3)-1 + R 4 + R • R eg =(1/10+1/10)-1 + 10 +20 = 35Ω

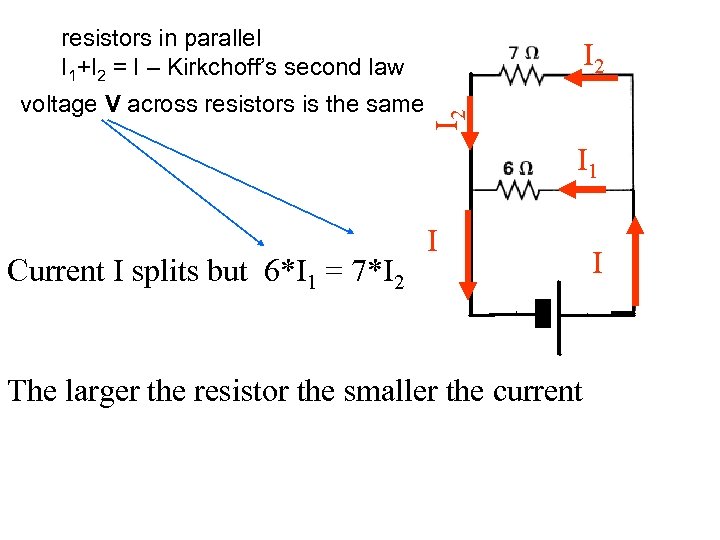resistors in parallel I 1+I 2 = I – Kirkchoff’s second law I 2 voltage V across resistors is the same I 2 I 1 Current I splits but 6*I 1 = 7*I 2 I The larger the resistor the smaller the current I

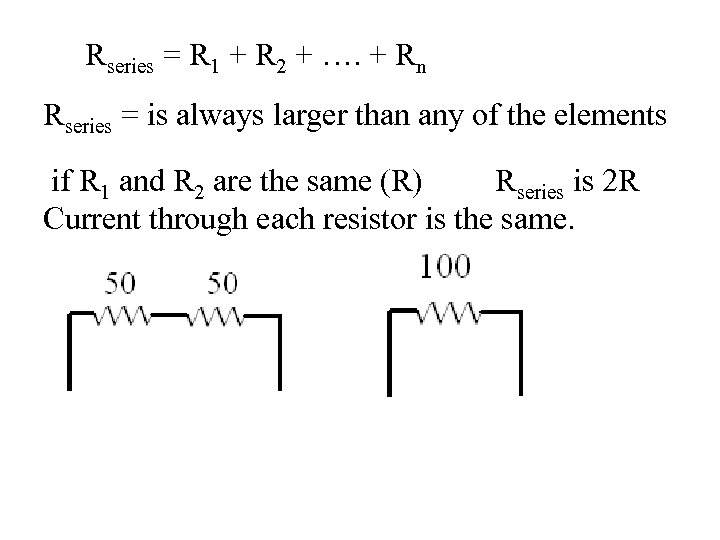Rseries = R 1 + R 2 + …. + Rn Rseries = is always larger than any of the elements if R 1 and R 2 are the same (R) Rseries is 2 R Current through each resistor is the same.

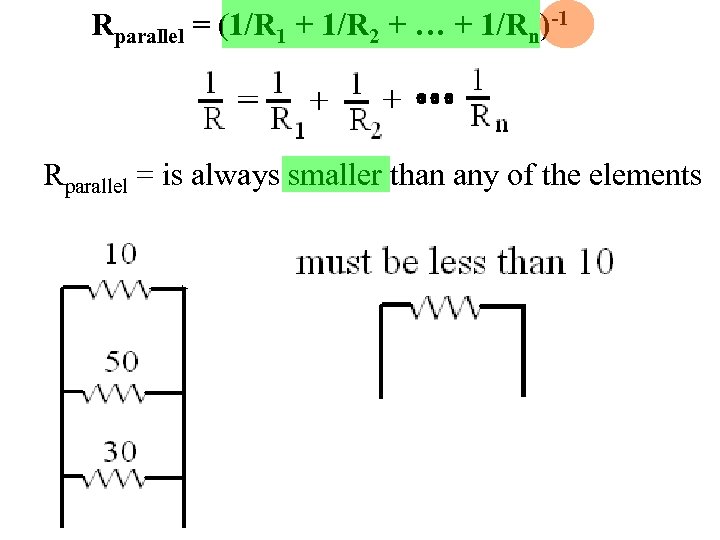Rparallel = (1/R 1 + 1/R 2 + … + 1/Rn)-1 Rparallel = is always smaller than any of the elements

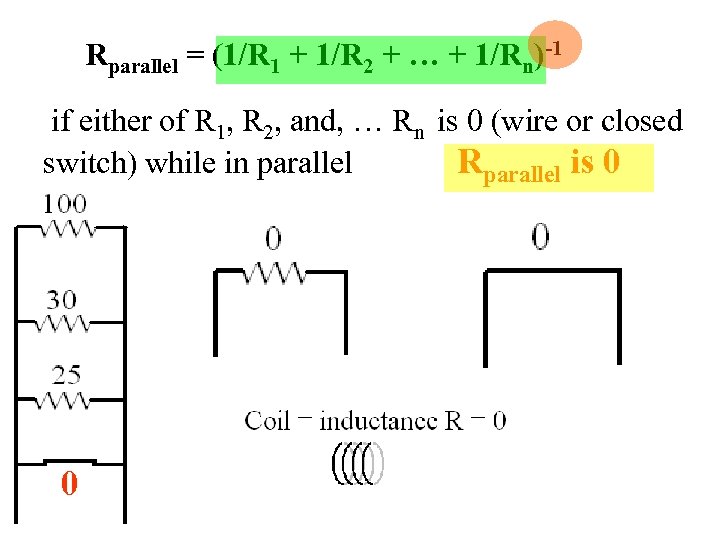Rparallel = (1/R 1 + 1/R 2 + … + 1/Rn)-1 if either of R 1, R 2, and, … Rn is 0 (wire or closed switch) while in parallel Rparallel is 0 0

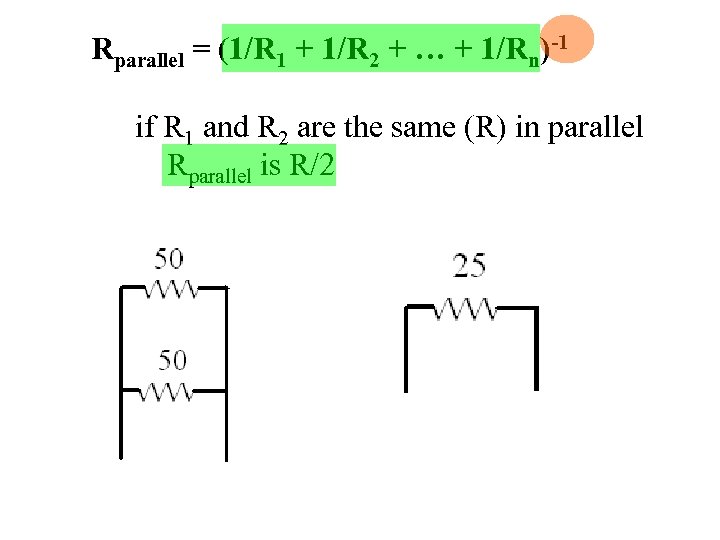Rparallel = (1/R 1 + 1/R 2 + … + 1/Rn)-1 if R 1 and R 2 are the same (R) in parallel Rparallel is R/2

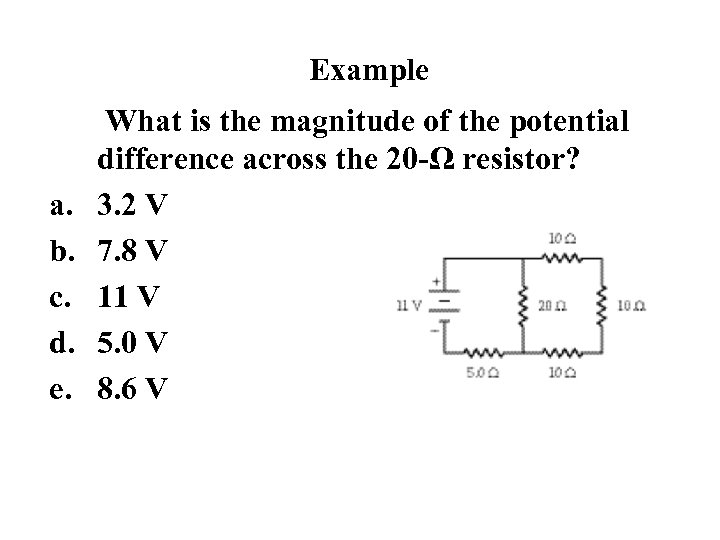Example a. b. c. d. e. What is the magnitude of the potential difference across the 20 -Ω resistor? 3. 2 V 7. 8 V 11 V 5. 0 V 8. 6 V

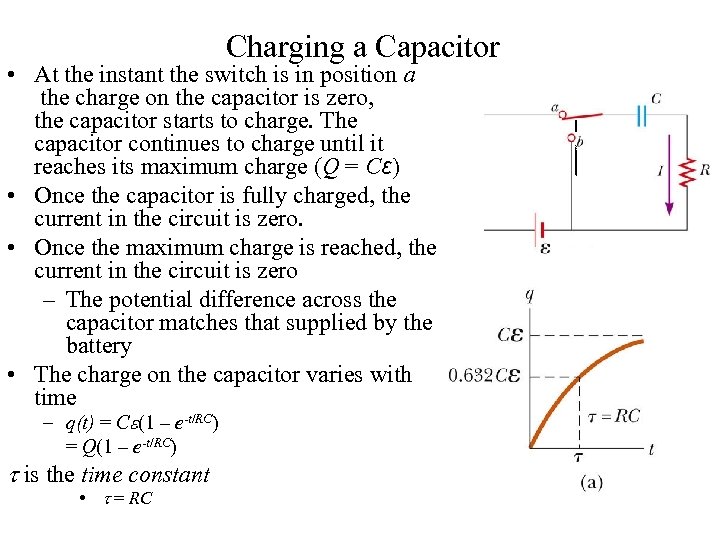Charging a Capacitor • At the instant the switch is in position a the charge on the capacitor is zero, the capacitor starts to charge. The capacitor continues to charge until it reaches its maximum charge (Q = Cε) • Once the capacitor is fully charged, the current in the circuit is zero. • Once the maximum charge is reached, the current in the circuit is zero – The potential difference across the capacitor matches that supplied by the battery • The charge on the capacitor varies with time – q(t) = Ce(1 – e-t/RC) = Q(1 – e-t/RC) is the time constant • = RC

Discharging a Capacitor in an RC Circuit • When a switch is thrown from a to b the charged capacitor C can discharge through resistor R – q(t) = Qe-t/RC • The charge decreases exponentially

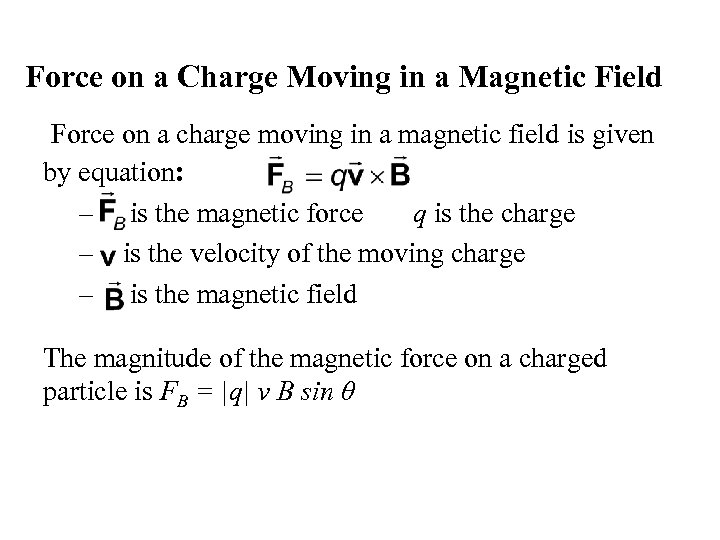Force on a Charge Moving in a Magnetic Field Force on a charge moving in a magnetic field is given by equation: – is the magnetic force q is the charge – is the velocity of the moving charge – is the magnetic field The magnitude of the magnetic force on a charged particle is FB = |q| v B sin θ

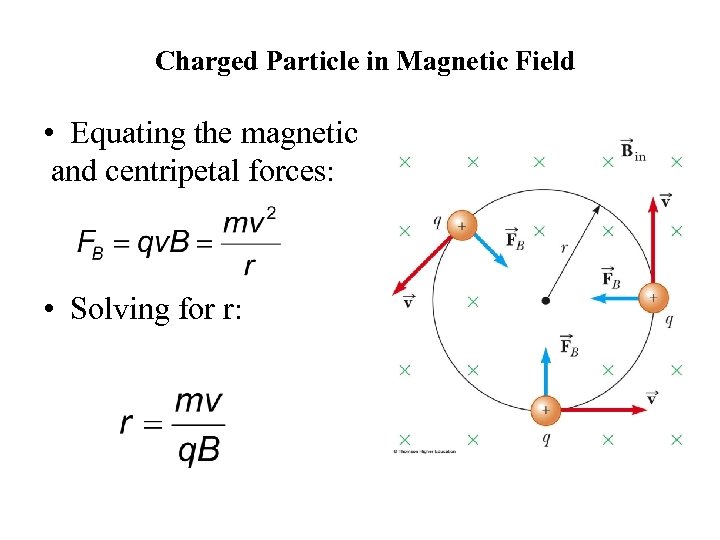Charged Particle in Magnetic Field • Equating the magnetic and centripetal forces: • Solving for r:

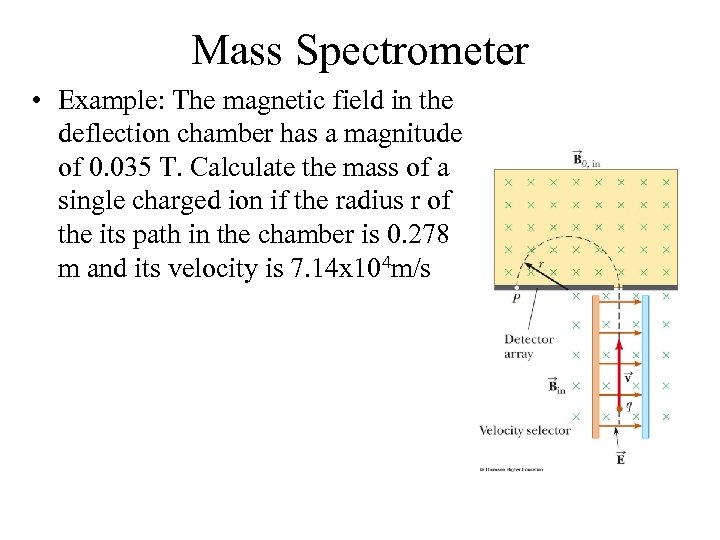Mass Spectrometer • Example: The magnetic field in the deflection chamber has a magnitude of 0. 035 T. Calculate the mass of a single charged ion if the radius r of the its path in the chamber is 0. 278 m and its velocity is 7. 14 x 104 m/s

Inductance, Inductors Inductance, unit: henry [H] = ability to store magnetic energy A circuit element that has a large self-inductance is called an inductor. The circuit symbol is Potential across inductor: v. L(t) = L di. L(t) / dt L = N 2 μA / ℓ UM = ½LI 2 Lparallel = (1/L 1 + 1/L 2 + … + 1/Ln)-1 Lseries = L 1 + L 2 + …. + Ln

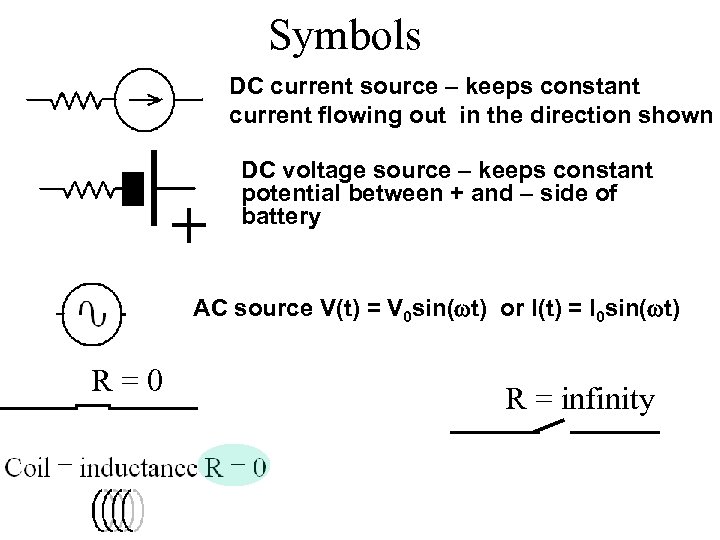Symbols DC current source – keeps constant current flowing out in the direction shown DC voltage source – keeps constant potential between + and – side of battery AC source V(t) = V 0 sin(wt) or I(t) = I 0 sin(wt) R=0 R = infinity

Complex Numbers rectangular form z=a+jb, z=zcosθ+jzsinθ) phasor form z=c/θ c = (a 2+b 2)½ θ = tan-1(b/a) z 1+z 2 = (a 1+a 2)+j(b 1+b 2) z 1·z 2= c 1·c 2/(θ 1+θ 2) z 1/z 2=c 1/c 2/(θ 1 -θ 2 ) AC circuits: impedance Z=R+j. X In series Zeq = (R 1+R 2)+j(X 1+X 2) In parallel Zeq=[1/(R 1 +j. X 1)+1/(R 2 +j. X 2)]-1

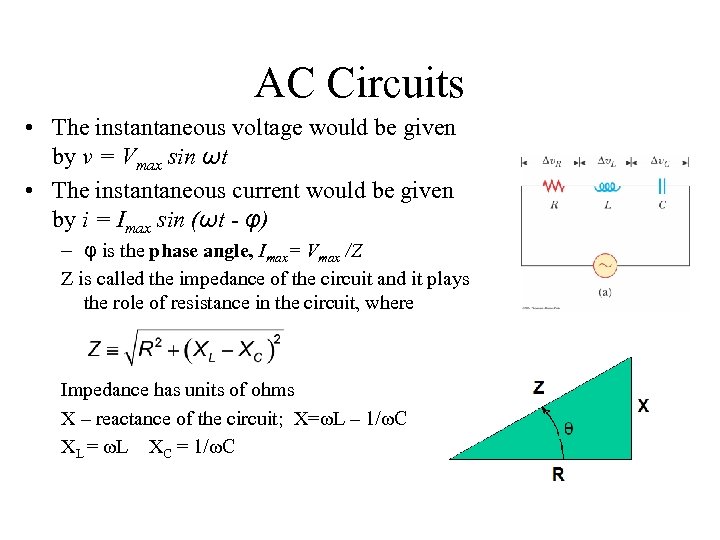AC Circuits • The instantaneous voltage would be given by v = Vmax sin ωt • The instantaneous current would be given by i = Imax sin (ωt - φ) – φ is the phase angle, Imax= Vmax /Z Z is called the impedance of the circuit and it plays the role of resistance in the circuit, where Impedance has units of ohms X – reactance of the circuit; X=ωL – 1/ωC XL = ωL XC = 1/ωC

AC Circuits Root mean square value of V and I is given by expressions: Vrms = Vmax/√ 2 , Irms = Imax /√ 2 Z=V/I θ =tan-1(X/R) V = Vrms sin ωt, I = Irmssin (ωt+ θ) in phasor form V=Vrms∟ 0 I = Irms∟θ Impedance in rectangle form: Z =R+j. X X=XL-Xc Xc = 1/(ωC) XL = ωL

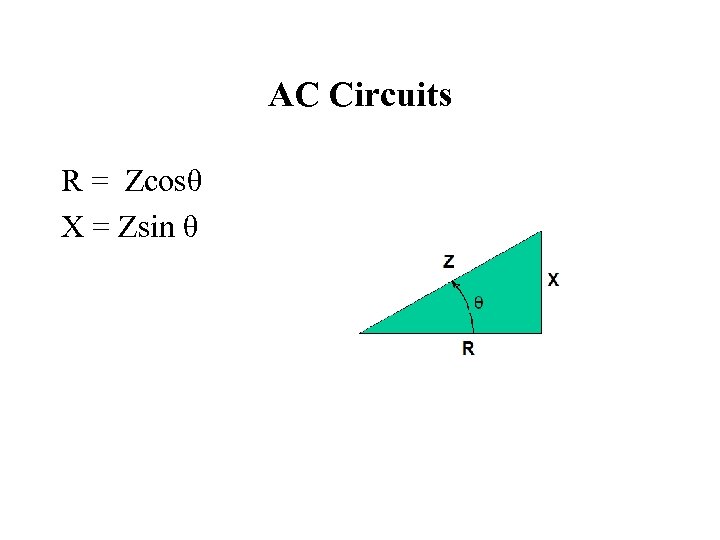AC Circuits R = Zcosθ X = Zsin θ

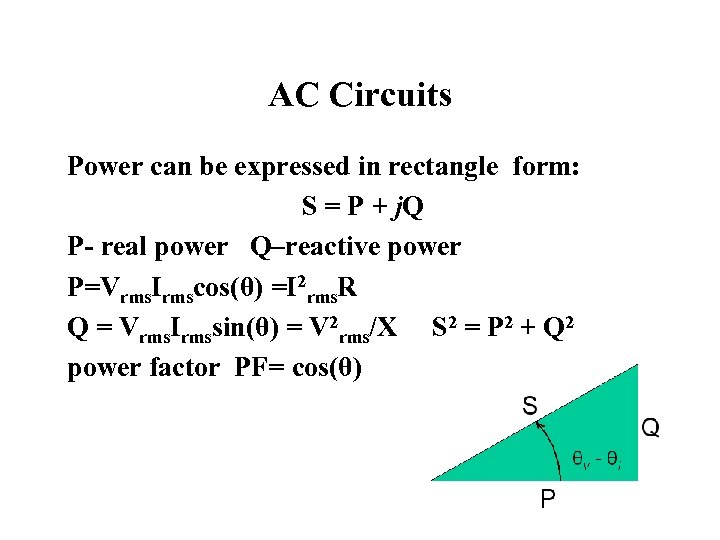AC Circuits Power can be expressed in rectangle form: S = P + j. Q P- real power Q–reactive power P=Vrms. Irmscos(θ) =I 2 rms. R Q = Vrms. Irmssin(θ) = V 2 rms/X S 2 = P 2 + Q 2 power factor PF= cos(θ)

Example A series RLC circuit has R = 425 Ω, L = 1. 25 H C = 3. 5 μF. It is connected to and AC source with f = 60 Hz and Vmax = 150 V a. Find the impedance of the circuit. b. Find the phase angle. c. Find the current in the circuit.

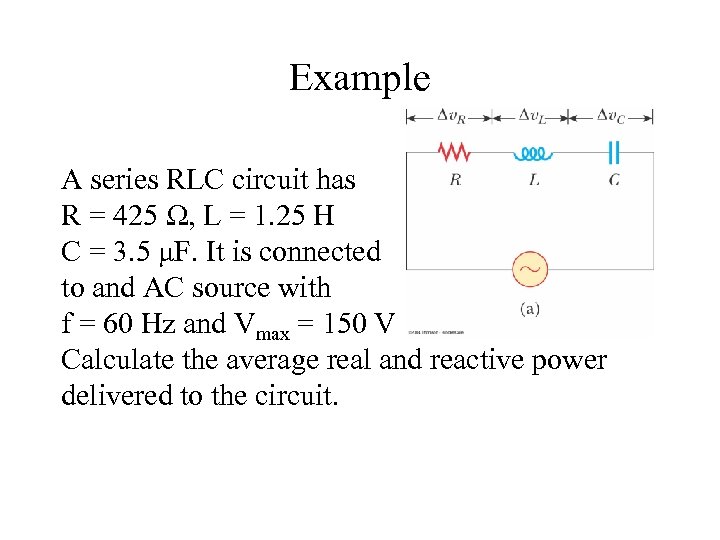Example A series RLC circuit has R = 425 Ω, L = 1. 25 H C = 3. 5 μF. It is connected to and AC source with f = 60 Hz and Vmax = 150 V Calculate the average real and reactive power delivered to the circuit.

sin(wt-q) sin(wt+q)

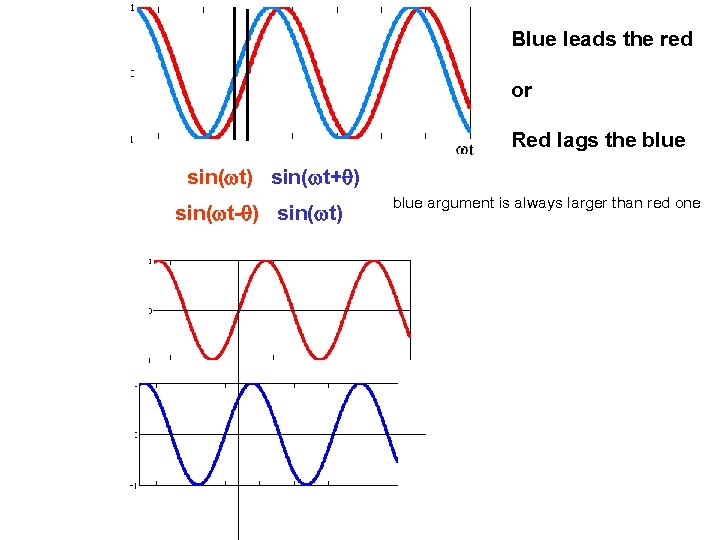Blue leads the red or Red lags the blue sin(wt) sin(wt+q) sin(wt-q) sin(wt) blue argument is always larger than red one

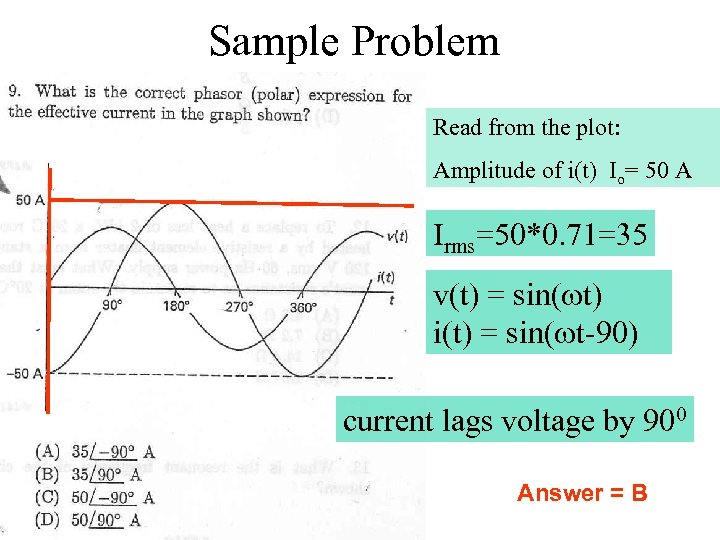Sample Problem Read from the plot: Amplitude of i(t) Io= 50 A Irms=50*0. 71=35 v(t) = sin(wt) i(t) = sin(wt-90) current lags voltage by 900 Answer = B

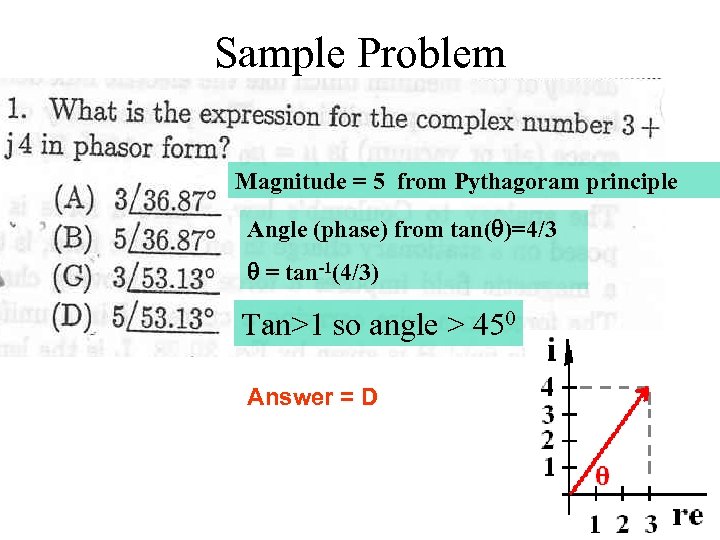Sample Problem Magnitude = 5 from Pythagoram principle Angle (phase) from tan(q)=4/3 q = tan-1(4/3) Tan>1 so angle > 450 Answer = D

Sample Problem Information 10 k. V power line is useless. It is not the potential difference between two ends of the wire. You must use P = I 2 R to calculate the power dissipated. Answer = C

Sample Problem • For AC circuit with Vrms=115 V, Irms = 20. 1 A and phase constant θ=320, find the average real power and average reactive power drawn by the circuit. P = 115 V*20. 1 Acos 320 = 1965 W Q = 115 V*20. 1 Asin 320 = 1217 k. VAR ( kilovolt -amps reactive)

Sample Problem Answer = A

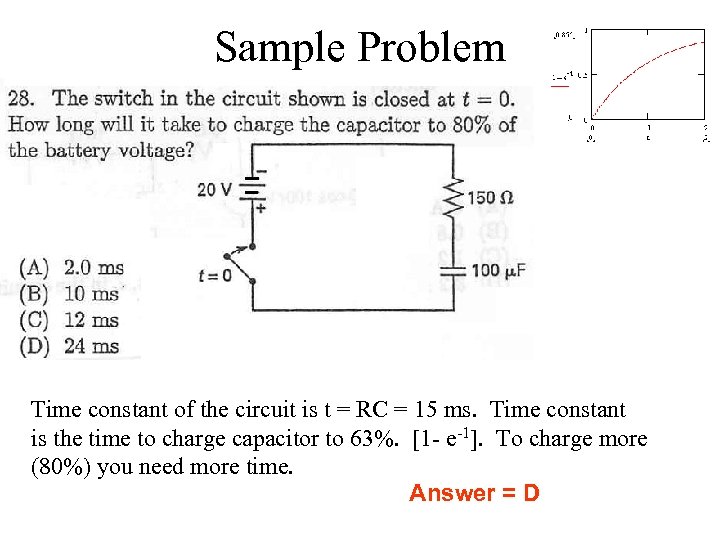Sample Problem Time constant of the circuit is t = RC = 15 ms. Time constant is the time to charge capacitor to 63%. [1 - e-1]. To charge more (80%) you need more time. Answer = D

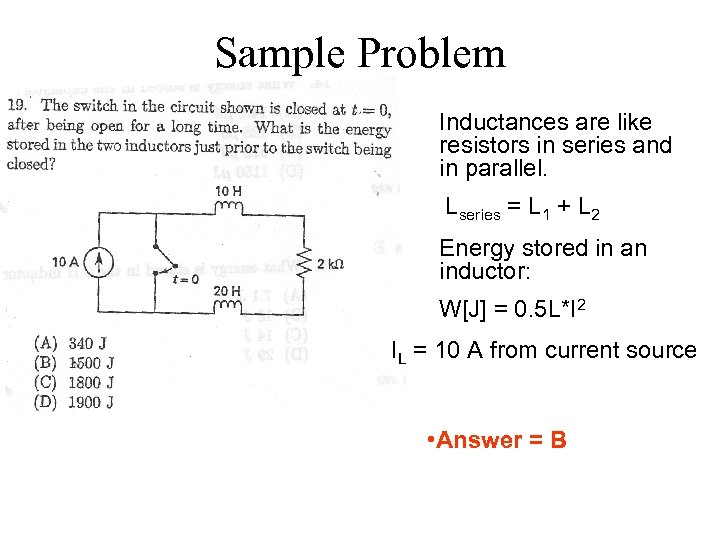Sample Problem Inductances are like resistors in series and in parallel. Lseries = L 1 + L 2 Energy stored in an inductor: W[J] = 0. 5 L*I 2 IL = 10 A from current source • Answer = B

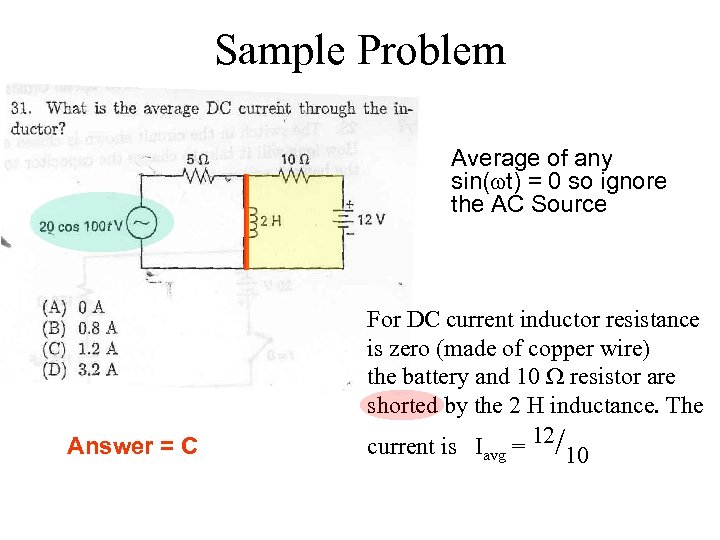Sample Problem Average of any sin(wt) = 0 so ignore the AC Source Answer = C For DC current inductor resistance is zero (made of copper wire) the battery and 10 resistor are shorted by the 2 H inductance. The current is Iavg = 12/10

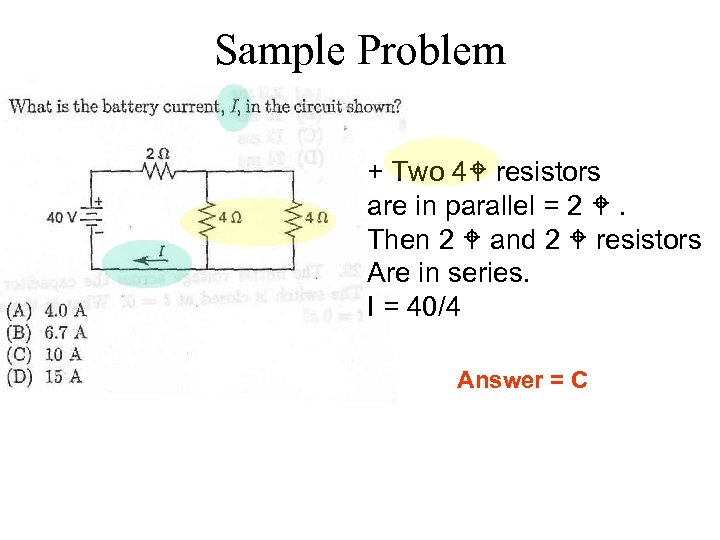Sample Problem + Two 4 resistors are in parallel = 2 . Then 2 and 2 resistors Are in series. I = 40/4 Answer = C

Sample Problem 20 is the amplitude Answer = B Power in AC circuits is calculated using rms values (this is why the rms was introduced) rms value is 20*0. 7 = 14. P=I 2 R = 14250 = 10 k. W.

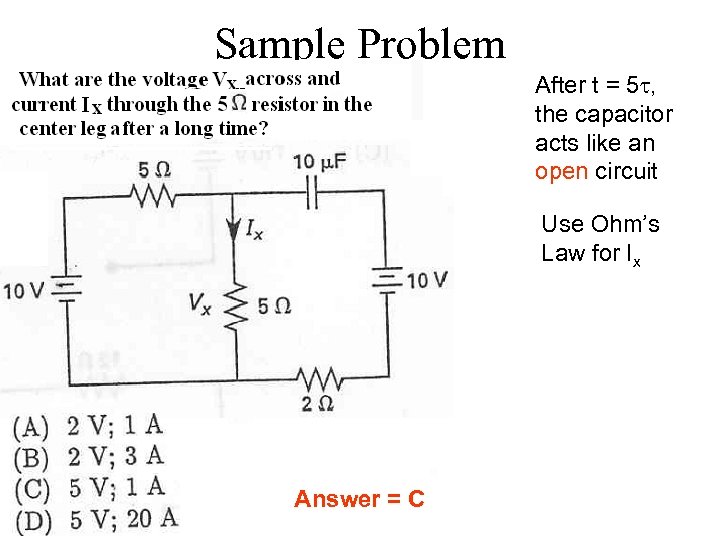Sample Problem After t = 5 t, the capacitor acts like an open circuit Use Ohm’s Law for Ix Answer = C