ФБГОУ ВПО Нижегородский государственный технический университет им Р

ФБГОУ ВПО «Нижегородский государственный технический университет им. Р. Е. Алексеева» Кафедра «Материаловедение, технологии материалов и термическая обработка металлов» Теория строения материалов комплект демонстрационных материалов к курсу лекций для студентов направления «Материаловедение и технологии материалов» очной и очно заочной форм обучения Составитель: доц. Костромин С. В. 2017 1

Литература • Лахтин Ю. М. , Леонтьева В. П. Материаловедение. – М. : Альянс, 2013. • Фетисов Г. П. , и др. Материаловедение и технология металлов. М. : Высшая Школа, 2008. • Материаловедение / Под ред. Б. Н. Арзамасова. – М. : МГТУ им. Баумана, 2008. • Научные основы материаловедения /Б. Н. Арзамасов и др. – М. : МГТУ им. Баумана, 1994. • Розин К. М. Практическая кристаллография. М. : МИСи. С, 2005. • Орлов А. Н. Введение в теорию дефектов в кристаллах. М. : Высшая школа, 1983. • Новиков И. И. , Розин К. М. Кристаллография и дефекты кристаллической решетки. – М. : Металлургия, 1990. 2

• Осинцев О. Е. Диаграммы состояния двойных и тройных систем. Фазовые равновесия в сплавах. – М. : Машиностроение, 2009. • Горелик С. С. , Добаткин С. В. , Капуткина Л. М. Рекристаллизация металлов и сплавов. – М. : МИСи. С, 2005. • Бокштейн Б. С. , Ярославцев А. Б. Диффузия атомов и ионов в твёрдых телах. – М. : МИСи. С, 2005. • Пикунов М. В. Плавка металлов, кристаллизация сплавов, затвердевание отливок. – М. : МИСи. С, 2005. • Теория строения материалов: Лабораторный практикум / Сорокин В. К. , Гаврилов Г. Н. , Алибеков С. Я. , Крашенинникова Н. Г. , Костромин С. В. , Терещенко Е. Г. , Мальцев И. М. , Колосова Т. М. – Йошкар Ола: Изд во ПГТУ, 2014. – 244 с. 3

Ссылка на Яндекс диск с материалами по курсу ТСМ: https: //yadi. sk/d/ZSks 2 Cz. Pdaq. DS 4

Цели и задачи освоения дисциплины. Дисциплина «Теория строения материалов» обеспечивает подготовку бакалавров по направлению 22. 03. 01 «Материаловедение и технологии материалов» и формирование знаний, умений и навыков, необходимых для применения материалов и технологических процессов их обработки при исполнении своих профессиональных обязанностей. • Предметом дисциплины являются конструкционные и инструментальные металлические, неметаллические и композиционные материалы. • Целью преподавания дисциплины является формирование компетенций в области строения и свойств основных конструкционных, инструментальных материалов, а также материалов с особыми свойствами, которые применяются в различных отраслях промышленности. 5

• Задачами преподавания дисциплины: - формирование знаний о физических, химических, механических, технологических и эксплуатационных свойствах различных материалов; - формирование знаний о поведении материалов при различном внешнем воздействии на них; - выработка навыков по правильному выбору материалов для заданной конструкции детали на основании анализа эксплуатационных требований, выбору способов её обработки; - ознакомление с методами исследования, с ГОСТами и другими нормативными документами Российской Федерации по конструкционным, инструментальным материалам и материалам с особыми свойствами. • 6

- - В результате освоения дисциплины обучающийся должен: • знать: основные классы современных материалов; современные теории строения материалов; связь химического состава, структуры и свойств материалов различных классов; основы теорий: строения атома, кристаллизации, диффузии, фазовых превращений, дислокационной теории; основы принципа выбора материалов, основные явления, происходящие в материалах при металлургических процессах производства, обработке давлением и термического упрочнения, особенности этапов жизненного цикла материалов и изделии из них. • уметь: определять по диаграмме состояния состав и количество фаз в сплавах, температуры фазовых переходов; рассчитывать параметры кристаллических решёток различных сингоний; рассчитывать параметры диффузионных процессов; определять структуру и фазовый состав сплавов различных типов проводить оценку структурных изменений материалов по изменению их структурно-зависимых физических свойств; выбрать класс материала по требуемым значениям свойств. 7

- • владеть: навыками работы со справочной литературой и технической документацией. навыками анализа макро- и микро структуры сталей и сплавов. умением оценить механические и технологические свойства материалов. умением оценить влияние структурных и технологических факторов на свойства материалов. • приобрести опыт: в научно исследовательской, расчетноаналитической, производственной и организационно-управленческой деятельности. 8

Материаловедение – наука, изучающая связь между химическим составом, структурой и свойствами материалов и изменение этих свойств при различных воздействиях на материал. С ↔ С Классификация материалов По агрегатному состоянию: Газообразные Жидкие Твёрдые По применению: Конструкционные Инструментальные С особыми свойствами По внутреннему строению: Кристаллические Аморфные По физико химической природе: Металлические Неметаллические Композиционные 9

Агрегатное состояние вещества (на примере кислорода О 2) 10

Модель расположения частиц в веществе а) кристалл б) жидкость в) газ 11

Поведение при нагреве кристаллического и аморфного вещества 12

Требования, предъявляемые к материалам: Эксплуатационные Технологические Экономические 13

Механические свойства Прочность – способность материала сопротивляться деформации и разрушению под действием внешних и внутренних напряжений. Истинный предел текучести σт определить трудно: не у всех металлов образуется «площадка текучести» . Поэтому чаще всего определяют условный предел текучести σ0, 2 который вызывает остаточную деформацию 0, 2 % σт. ~ σ0, 2 Прочностные расчеты чаще ведут по пределу текучести, так как значительная пластическая деформация большинства деталей и конструкций недопустима. Но и предел прочности знать необходимо, так как он показывает, при каком напряжении начнется разрушение 14

Механические свойства 15

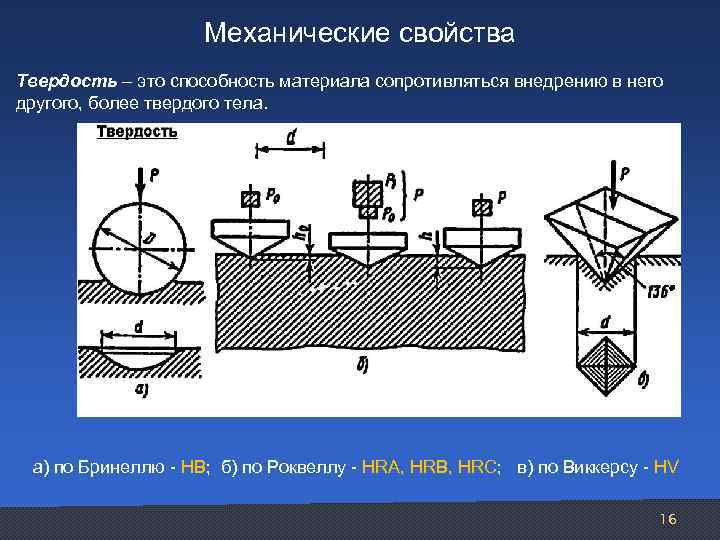
Механические свойства Твердость – это способность материала сопротивляться внедрению в него другого, более твердого тела. а) по Бринеллю HB; б) по Роквеллу HRA, HRB, HRC; в) по Виккерсу HV 16

Механические свойства Вязкость – способность материала сопротивляться разрушению при ударных, динамических нагрузках. Характеристика вязкости определяется при испытании на ударный изгиб, при котором нагрузка прилагается к образцу с очень большой скоростью, за тысячные доли секунды. Испытание проводится на маятниковом копре. Тяжелый маятник, поднятый на определенный угол, отпускают. На пути движения маятника находится образец. Удар ножа маятника разрушает его. Произведенная при разрушении работа определяется как разность между потенциальной энергией маятника до и после испытания. Ударная вязкость – это работа разрушения образца, отнесенная к площади поперечного сечения: 17

Механические свойства Образец должен иметь надрез – концентратор напряжения. Обозначение ударной вязкости зависит от вида надреза Для одного и того же материала KCU > KCV > KCT, т. е. чем острее надрез, тем легче разрушается материал. Ударная вязкость тоже является критерием надежности материала, гарантией, что он не будет разрушаться хрупко, внезапно. Свойство металла хрупко разрушаться, терять вязкость при понижении температуры называется хладноломкостью. За характеристику хладноломкости принимают температурный порог хладноломкости t 50. Это температура, при которой величина ударной вязкости уменьшается вдвое. При этом излом имеет строение наполовину вязкое, наполовину хрупкое. 18

Механические свойства Многие детали – валы, оси, шестерни – испытывают переменные по величине и направлению нагрузки. Под действием многократно повторяющихся знакопеременных нагрузок в металле накапливаются повреждения, дефекты. Это явление называется усталостью. Напряжения, даже меньше σт , могут вызвать зарождение и рост усталостной трещины, возникающей на поверхности детали. Это постепенно приведет к разрушению. Выносливость – это способность металла противостоять усталости, сопротивляться разрушению при знакопеременных нагрузках. Характеристики выносливости определяются из испытаний на специальных машинах циклического действия. Нагрузка, действующая на каждую точку поперечного сечения образца, непрерывно меняется по величине и направлению. Пределом выносливости, или пределом усталости σ 1 называется наибольшее напряжение, которое не вызывает разрушения образца после заданного числа циклов нагружения. При испытании сталей стандартное число циклов нагружения N = 107, при испытании цветных металлов и сплавов N = 108. 19

Физические свойства • 20

Физические свойства Температура плавления – это температура, при которой нагреваемый металл полностью переходит из твердого состояния в жидкое при нормальном атмосферном давлении. Чистые металлы плавятся при определенных температурах, а большинство сплавов – в интервале температур, т. е. имеют начало и конец плавления. При этом температура плавления сплава, как правило, ниже температуры плавления самого легкого его компонента, а температура затвердевания понижается с увеличением концентрации растворенного вещества. Температура плавления имеет большое значение при выборе металлов для изготовления литых изделий, сварных и паяных соединений, термоэлектрических приборов и других изделий. 21

Физические свойства Теплопроводность [Вт/(м·К)] – это способность материала передавать тепло от более нагретых к менее нагретым участкам с той или иной скоростью. Чем больше теплопроводность, тем быстрее тепло при нагревании распространяется по всему объему материала. Лучше других металлов проводит тепло Ag – 425 Вт/(м·К). Самая низкая теплопроводность у Bi – 8, 41 Вт/(м·К). Учитывают теплопроводность при обработке материалов режущими инструментами, термообработке, газовой резке. А также при изготовлении нагревательных приборов, различных тепловых агрегатов (котлов, теплосетей и т. п. ), холодильников. 22

Физические свойства Теплоемкость [к. Дж/(кг·К)] – свойство материала поглощать при нагревании определенное количество теплоты и отдавать его при охлаждении. Характеризуется удельной теплоемкостью, т. е. количеством тепла (Дж), которое необходимо для повышения температуры 1 кг металла на 1 К. Удельная теплоемкость уменьшается с увеличением порядкового номера элемента в таблице Д. И. Менделеева. Самая высокая теплоемкость у воды – 4, 2 к. Дж/(кг·К). У металлических сплавов теплоемкость находится в пределах 0, 1… 2, 0 к. Дж/(кг·К), большинства металлов – 0, 3… 0, 4 к. Дж/(кг·К). Учитывается теплоемкость при расчете процессов нагрева или охлаждения металлов. 23

Физические свойства Тепловое расширение – способность материалов изменять в процессе нагревания или охлаждения свои размеры при постоянном давлении. В основе теплового расширения лежит несимметричность тепловых колебаний атомов, поэтому при повышении температуры увеличиваются средние межатомные расстояния. Характеристиками теплового расширения являются температурные коэффициенты линейного или объемного расширения. Коэффициент линейного теплового расширения характеризует изменение линейного размера (длины) при изменении температуры на один градус. У металлов коэффициент линейного теплового расширения в интервале температур 0… 100 °С изменяется в широких пределах: от 4, 57· 10– 6 у Os до 10– 4 К– 1 – у Sr. С повышением температуры коэффициент линейного расширения возрастает. Тепловое расширение металлов необходимо учитывать при ковке, горячей объемной штамповке, сварке изделий, прокладке трубопроводов и рельсов железнодорожных путей, соединении мостовых ферм и других металлических конструкций. 24

Физические свойства Электропроводность способность металлов проводить электрический ток под действием внешнего электрического поля. Наибольшей электропроводностью обладают чистые металлы – Cu, Al, Fe. У сплавов электропроводность ниже. Характеристикой противоположной электропроводности является электросопротивление – свойство материала проводника препятствовать прохождению через него электрического тока. Характеризуется удельным электрическим сопротивлением [Ом·м], т. е. сопротивлением однородного отрезка проводника длиной 1 м и площадью токоведущего сечения 1 м 2. В технике применяется чаще всего в миллион раз меньшая производная единица – Ом·мм 2/м К металлам с высоким электрическим сопротивлением относят W, Cr, Ni. Из сплавов на их основе изготовляют электронагревательные элементы. 25

Металлы и сплавы Из 117 элементов периодической системы элементов ¾ обладают металлическими свойствами Распространенность элементов в земной коре 26

Классификация металлов и сплавов 27

Температура плавления металлов 28

Плотность металлов 29

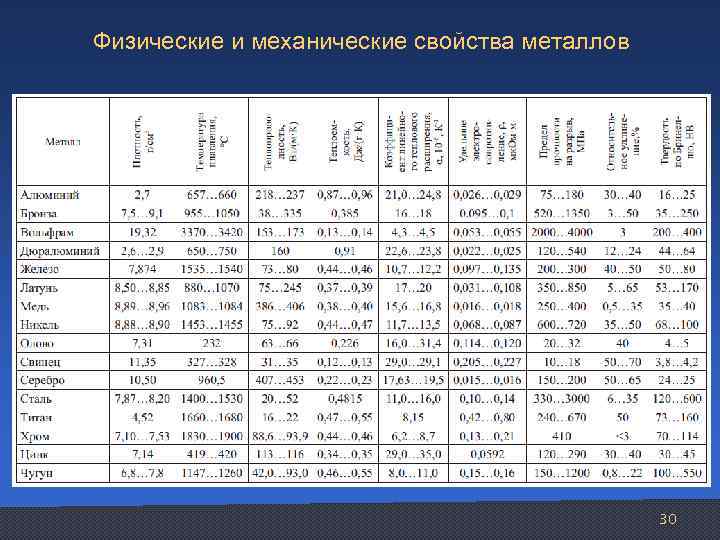
Физические и механические свойства металлов 30

Общие свойства металлических материалов 1. Металлические материалы, получаемые традиционным способом, являются кристаллическими веществами. 2. Для металлов характерен металлический тип связи между атомами в кристалле. 3. Металлы хорошо проводят тепло, электричество, имеют характерный блеск, способны к термоэлектронной эмиссии, имеют положительный температурный коэффициент электросопротивления. 4. Металлы способны к пластической деформации. 31

«Металлы суть светлые тела, которые ковать можно. Таких тел находим только шесть…» (М. В. Ломоносов, 1763) 32

Методы исследования структуры материалов макроанализ микроанализ рентгеноструктурный анализ 33

Уровни структуры металлических материалов Уровень структуры Макроструктура Метод исследования Увеличение Разрещающая способность d, нм Макроанализ до х100 Оптическая микроскопия х100 2000 до 200 Микроструктура Электронная микроскопия х2000 50000 200 0, 5 Тонкая структура Дифракционные методы более х50000 ~ 0, 1 34

Кристаллическая решётка Это совокупность воображаемых линий и плоскостей, проходящих через центры наиболее вероятного расположения частиц вещества в пространстве. Элементарная ячейка – наименьший объём, трансляцией которого можно построить весь кристалл целиком 35

Сингонии P – примитивная, С– базоцентрированная, I – объемно центрированная, F гранецентрированная 36

Решётки Бравэ П БЦ ОЦ ГЦ 37

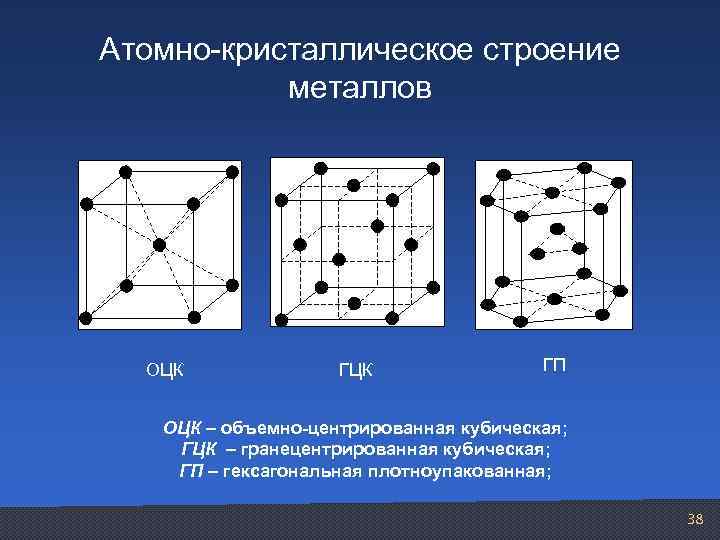
Атомно кристаллическое строение металлов ОЦК ГЦК ГП ОЦК – объемно-центрированная кубическая; ГЦК – гранецентрированная кубическая; ГП – гексагональная плотноупакованная; 38

Объёмноцентрированная кубическая решётка W, Mo, Cr, V, K, Na, Li, -Ti, -Fe, Ta 39

Гранецентрированная кубическая решётка Al, Cu, Ni, Ag, Au, Pb, -Fe, Pd, Ir, Ce 40

Гексагональная плотноупакованная решётка Mg, Zn, Ti, Cd, Be, Zr, Os 41

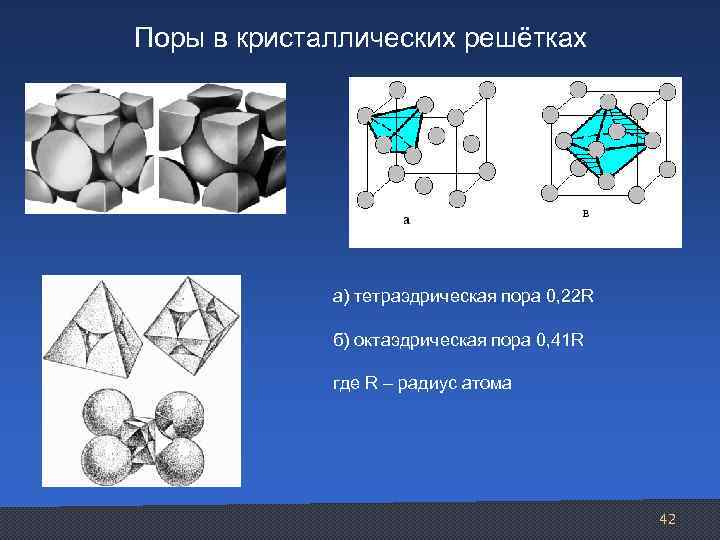
Поры в кристаллических решётках а) тетраэдрическая пора 0, 22 R б) октаэдрическая пора 0, 41 R где R – радиус атома 42

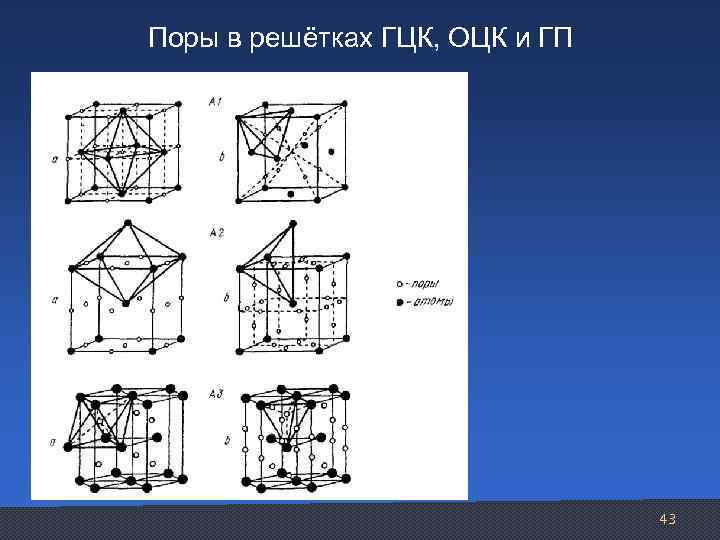
Поры в решётках ГЦК, ОЦК и ГП 43

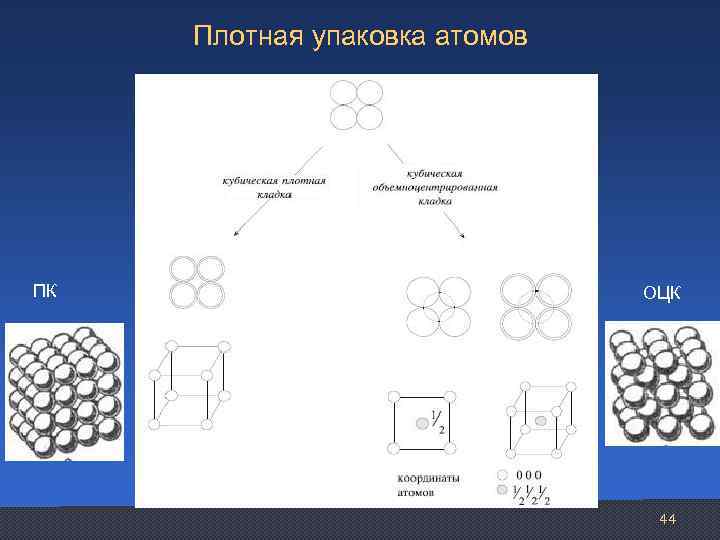
Плотная упаковка атомов ПК ОЦК 44

Плотнейшая упаковка атомов ГП ГЦК А В А А С В А 45

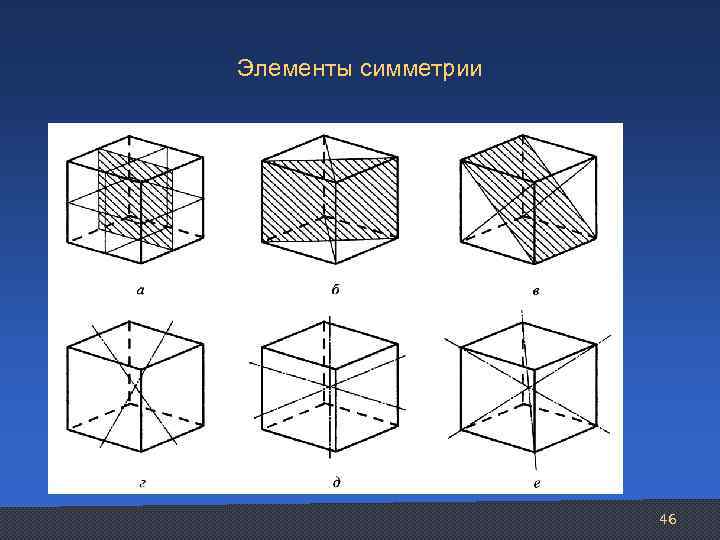
Элементы симметрии 46

Индексы узлов 47

Индексация атомных плоскостей. Индексы Миллера 48

Совокупность (семейство) плоскостей Непараллельные плоскости, имеющие одинаковое атомное строение (количество атомов и их расположение), кристаллографически эквивалентны. Всю совокупность эквивалентных плоскостей обозначают индексом какой либо одной плоскости, заключенным в фигурные скобки. Например, плоскости 100, 010, 001, 100, 010, 001. Их обозначают индексом одной какой либо плоскости и заключают в фигурные скобки как семейство плоскостей {100} или {001} 49

Индексы Миллера Бравэ 50

Индексы направлений Совокупность непараллельных кристаллографических направлений, эквивалентных по числу атомов, составляют семейство направлений. Его обозначают индексом одного из направлений и заключают в угловые скобки. Например, семейство шести ребер куба 100, 010, 001, 100, 010, 001 обозначают 100 . 51

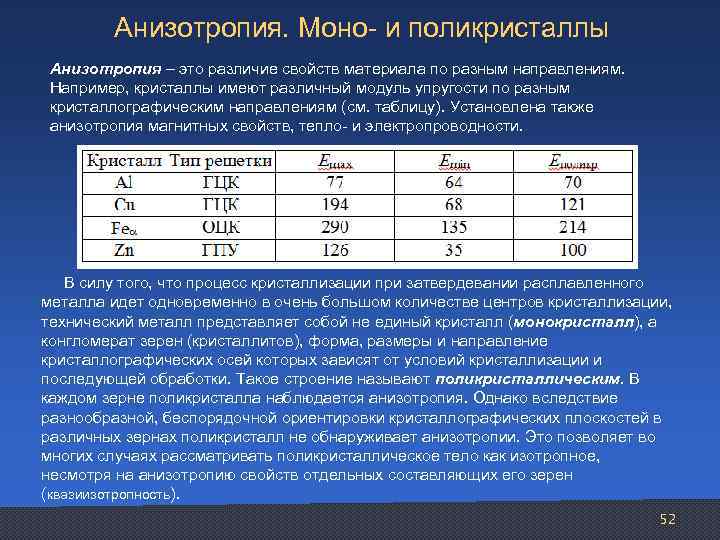
Анизотропия. Моно и поликристаллы Анизотропия – это различие свойств материала по разным направлениям. Например, кристаллы имеют различный модуль упругости по разным кристаллографическим направлениям (см. таблицу). Установлена также анизотропия магнитных свойств, тепло и электропроводности. В силу того, что процесс кристаллизации при затвердевании расплавленного металла идет одновременно в очень большом количестве центров кристаллизации, технический металл представляет собой не единый кристалл (монокристалл), а конгломерат зерен (кристаллитов), форма, размеры и направление кристаллографических осей которых зависят от условий кристаллизации и последующей обработки. Такое строение называют поликристаллическим. В каждом зерне поликристалла наблюдается анизотропия. Однако вследствие разнообразной, беспорядочной ориентировки кристаллографических плоскостей в различных зернах поликристалл не обнаруживает анизотропии. Это позволяет во многих случаях рассматривать поликристаллическое тело как изотропное, несмотря на анизотропию свойств отдельных составляющих его зерен (квазиизотропность). 52

Дефекты кристаллической решётки Три причины отсутствия идеальных кристаллов: Атомы вещества находятся в непрерывном тепловом колебательном движении; Нет идеально чистых веществ; У монокристаллов имеется поверхность, у поликристаллов – границы зёрен. Дефекты решётки классифицируют по размерному признаку: Точечные (нульмерные); Линейные (одномерные); Поверхностные (двумерные). 53

Дефекты кристаллической решётки: Точечные дефекты Вакансии Межузельные атомы Примесные атомы Комплексы Линейные дефекты Дислокации (краевые, винтовые, смешанные) Дисклинации Поверхностные дефекты Малоугловые границы Высокоугловые границы Дефекты упаковки Двойники 54

Точечные дефекты а) вакансия; б) межузельный атом Вакансии по Шоттки 55

Комплексы точечных дефектов дивакансии и тривакансии тетраэдр «гантель» краудион U 2 v<2 Uv 56

Линейные дефекты Предпосылки: 1. Сохранение в процессе пластической деформации кристаллической решётки. 2. Деформация распространяется по определённым плоскостям. 3. Расхождение значение теоретической и реальной прочности кристаллов. Металл. τ теорет, МПа τ действит, МПа Cu 7320 1, 0 Ag 4600 6, 0 Fe 11000 29 57

Модель трансляционного сдвига 58

Расчёт теоретической прочности кристалла по Френкелю (1924 г. ) Все атомы, находящиеся в плоскости сдвига, смещаются относительно другой атомной плоскости одновременно. Каждый атом в своем равновесном положении обладает минимумом энергии. Для его выведения из этого положения нужно приложить силу и затратить энергию. Энергия атома изменяется от минимума до максимума на пути « в/2» и снова от максимума до минимума на пути от « в/2» до « в» , т. е. график энергии есть периодическая функция. 59

Дислокации Несоответствие реального поведения кристаллов при механическом нагружении в модели Френкеля означает, что существуют факторы, значительно облегчающие процесс пластической деформации и уменьшающие критическое напряжение сдвига т. В 1934 г. Полани, Орован и Тейлор предположили, что такое несоответствие объясняется наличием в металлах особых дефектов – дислокаций. 60

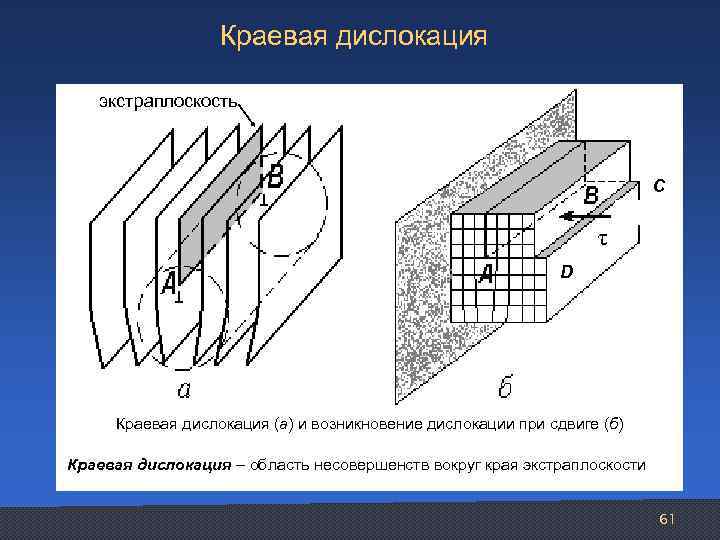
Краевая дислокация экстраплоскость С τ D Краевая дислокация (а) и возникновение дислокации при сдвиге (б) Краевая дислокация – область несовершенств вокруг края экстраплоскости 61

Краевая дислокация 62

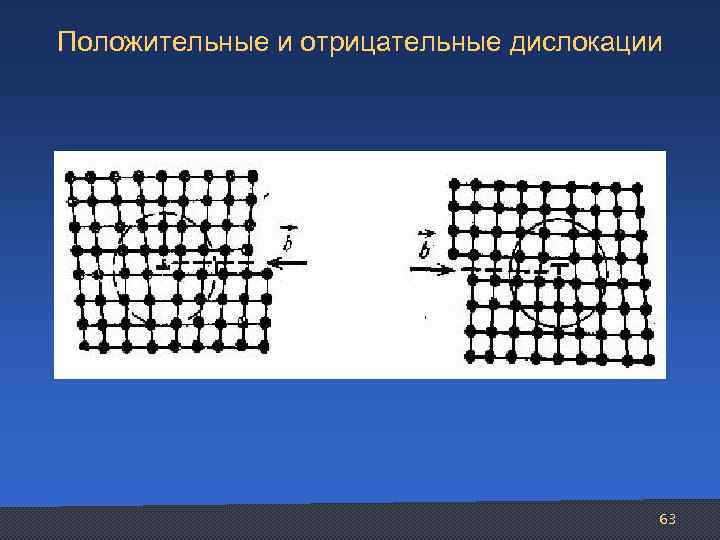
Положительные и отрицательные дислокации 63

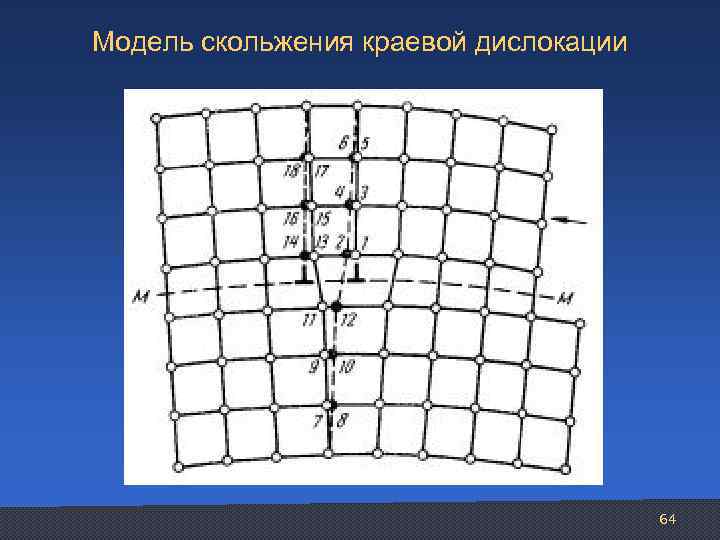
Модель скольжения краевой дислокации 64

Механизм пластической деформации 65

Движение дислокации в кристалле 66

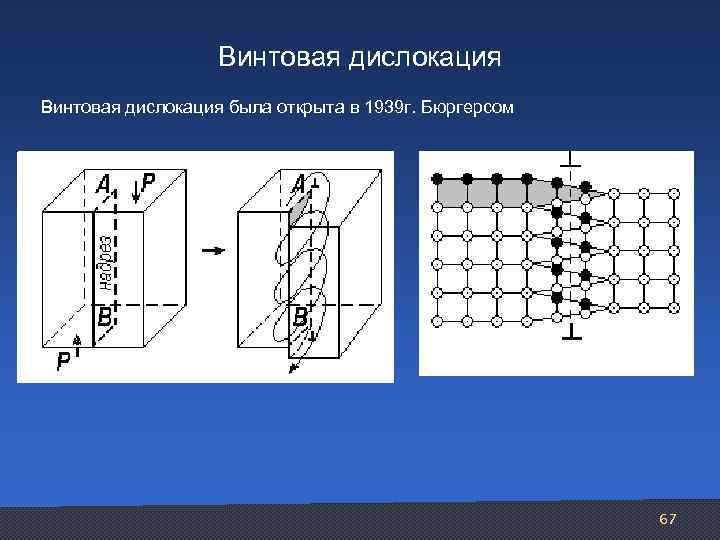
Винтовая дислокация была открыта в 1939 г. Бюргерсом 67

Винтовая дислокация 68

Модель скольжения винтовой дислокации 1. Дислокация перемещается на один период решетки вправо в результате пере движений атомов только внутри области несовершенства; атомы вне области несовершенства остаются на своих местах. 2. Дислокация перемещается на один период решетки вслед ствие передвижения атомов внутри ядра дислокации всего лишь на доли периода решетки. 3. В области ядра винтовой дислокации атомы смещаются в направлении действующих на них сил (вниз и вверх на рис. ), а сама дислокация перемещается перпендикулярно этому направ лению (вправо на ис. ). р 69

Смешанные дислокации 70

Ориентация дислокационных линий по отношению к направлению сдвига 71

Плотность дислокаций Выращенный массивный монокристалл высокой чистоты <103 Отожженный обычный монокристалл 104— 106 Отожженный поликристалл 107— 108 Металл после сильной холодной деформации 1011— 1012 В монокристаллических усах дислокации или совсем отсутствуют, или же в одном монокристалле находится только одна дислокация. 72

73

Модель Вольтерра Дислокации Вольтерра: а) исходный цилиндр с разрезом Г, б) краевая дислокация с вектором Бюргерса b , в) винтовая дислокация, г) клиновая дисклинация с вектором Франка ω, д) дисклинация кручения. Пусть есть однородный полый цилиндр с радиальным разрезом Г. Путем трансляции и разворота берегов разреза Г и последующей их склейки можно получить 4 дислокации Вольтерра. При этом в возникающие пустоты материал добавляется, а из областей перекрытия изымается. При уменьшении внутреннего отверстия в цилиндре возникает линейная сингулярность, которая и является линией дефекта. Первые два типа дислокаций Вольтерра, связанные с трансляцией на вектор b , являются дислокациями, а два других типа дислокаций Вольтерра, связанные с поворотом недеформированных берегов разреза на угол ω вокруг фиксированной оси, дисклинациями. Как для обозначения мощности дислокаций существует специальный термин вектор Бюргерса, так и для обозначения мощности дисклинаций (аксиального вектора ω) используется свой термин вектор Франка (или вектор поворота). Прямолинейные дисклинации с вектором Франка, параллельным линии дефекта, называют клиновыми, а дисклинаций с вектором Франка, перпендикулярным линии, — дисклинациями кручения. 74

Клиновые дисклинации г 75

Дисклинации кручения Если надрезать цилиндрический кристалл и поворачивать кромки разреза на вектор поворота, перпендикулярный к поверхности разреза, т. е. параллельный оси у, то возникает дисклинация кручения. Схема расположения атомов в районе дисклинации кручения показана на рис. д). Характеристиками дисклинации служат пространственное расположение линии дисклинации и вектор поворота. У дисклинаций кручения будет разный знак в случае, когда векторы поворота равны по величине и противоположны по направлению. Клиновая дисклинация имеет положительный знак, если она образована извлечением клина из кристалла, и отрицательный – при внедрении клина в кристалл. 76

Свойства дисклинаций Появление дисклинации повышает внутреннюю энергию кристалла. Дисклинация имеет энергию, превышающую энергию дислокации почти на четыре порядка, поэтому дисклинации образуются труднее, чем дислокации. Дисклинации взаимодействуют друг с другом. Две дисклинации одного знака отталкиваются, разных знаков — притягиваются. Сила взаимодействия клиновых дисклинации примерно в четыре раза больше, чем дисклинации кручения. Характер взаимодействия дисклинации с дислокациями зависит от взаимной ориентации вектора поворота и вектора Бюргерса и расположения дислокации. При этом возможно: Переползание и скольжение дислокации. Вращение дислокации, которое приводит к сдвигу части кристалла на угол относительно первоначального положения. Пересечение дисклинации движущейся дислокацией. Приводит к образованию порогов. Поглощение дислокации дисклинацией с образованием дисклинационно дислокационного комплекса. Дисклинации взаимодействуют с точечными дефектами. Вакансия притягивается к отрицательной клиновой дисклинации и отталкивается от положительной. Как и дислокации, дисклинации переползают в кристалле, поглощая или испуская точечные дефекты. Дисклинации возникают в кристалле при пластической деформации. Источник дисклинаций аналогичен источнику дислокаций Франка – Рида. 77

Поверхностные дефекты 78

Границы зерен Граница зерна – это не «стена» из чего то между соседними зернами и не пустота между ними. Это область, где нарушается строго упорядоченное строение металла: атомные плоскости в одном зерне не имеют продолжения в соседнем, там атомные плоскости расположены в другом направлении. Границы зерен – не линии, хотя именно так мы видим их на отполированной и протравленной поверхности металла. Это поверхности раздела между зернами, представляющими собой неправильные многогранники. Каждое зерно как бы «завернуто» в свою границу. Границы зерен и субзерен являются препятствиями для развития деформации, а значит – упрочняют металл. Чем больше поверхность границ в единице объема, тем прочнее металл. Понятно, что в мелкозернистом металле площадь поверхности границ больше, чем в крупнозернистом. Поэтому мелкозернистый металл обладает более высокими механическими свойствами по сравнению с крупнозернистым. 79

Границей зерен называют поверхность, по обе стороны от которой кристаллические решетки различаются пространственной ориентацией. Эта поверхность является дву мерным дефектом, имеющим макроскопические размеры в двух измерениях и атомные —в третьем измерении. Взаимную ориентацию решеток соседних зерен часто характеризуют, указывая общее для обоих зерен кристаллографическое направление [uvw] и угол поворота ω вокруг него, который приводит к параллельности решеток соседних зерен. Если ось вращения лежит в плоскости границы зерен, то такую границу называют границей наклона, а если ось вращения перпендикулярна плоскости границы, то границей кручения. 80

Границы с разориентацией соседних зерен менее ~7 о относят к малоугловым, а с большей разориентацией – к высокоугловым. Зёрна Блоки или субзёрна 81

Малоугловые границы Имеют дислокационное строение, угол разориентировки не превышает 7 о 82

Несимметричная малоугловая граница наклона Если малоугловая граница лежит несимметрично, то строение ее усложняется, так как на ней оканчиваются две группы плоскостей, образующие две серии краевых дислокаций 83

Малоугловая граница кручения образуется рядами винтовых дислокаций (на рис. черные кружки обозначают атомы ниже плоскости границы, а светлые – выше ее). Граница не может состоять из одного ряда параллельных винтовых дислокаций, так как такой ряд был бы нестабильным. Граница кручения образована сеткой двух взаимно перпендикулярных рядов винтовых дислокаций. Как и в малоугловой границе наклона, здесь также между участками с несовершенной решеткой (областями ядер дислокаций) имеются участки упругого сопряжения решеток соседних зерен. На рис. такие участки расположены внутри ячеек дислокационной сетки. 84

Малоугловые границы возникают при росте кристаллов из расплава, при пластической деформации и при дорекристаллизационном отжиге после холодной деформации. Образование стенок дислокаций, приводя щее к подразделению кристалла на субзерна – полигоны (мно гоугольники), было названо полигонизацией 85

Высокоугловые границы При углах разориентировки, превышающих 7°, плотность дислокаций на границах зерен становится столь высокой, что ядра дислокаций сливаются, и дальнейшее описание границ при помощи решеточных дислокаций становится невозможным. Такие границы называют высокоугловыми. Участки материала, отделенные высокоугловыми границами, называют зернами или кристаллитами. Тело, состоящее из множества кристаллитов, является поликристаллом. Теория аморфной прослойки – 1900 г Модель переходной решётки – 1929 г. Теория специальных и произвольных границ – 1949 г. 5 атомных диаметров 86

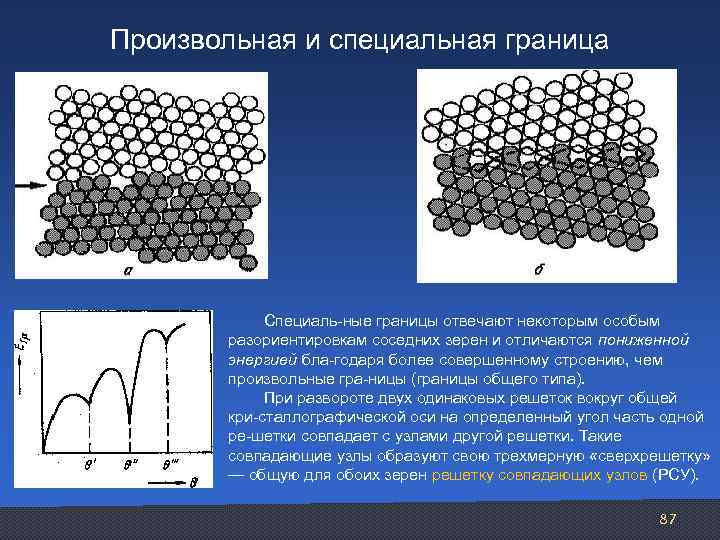
Произвольная и специальная граница Специаль ные границы отвечают некоторым особым разориентировкам соседних зерен и отличаются пониженной энергией бла годаря более совершенному строению, чем произвольные гра ницы (границы общего типа). При развороте двух одинаковых решеток вокруг общей кри сталлографической оси на определенный угол часть одной ре шетки совпадает с узлами другой решетки. Такие совпадающие узлы образуют свою трехмерную «сверхрешетку» — общую для обоих зерен решетку совпадающих узлов (РСУ). 87

Модель совпадающих узлов Модель релаксированной границы В модели жестких сфер нерелаксированная идеальная гра ница совпадающих узлов не может соответствовать минимуму энергии. Чтобы в пределах сегмента Р уменьшить сумму энергий парных взаимодействий атомов соседних кристаллов, необходимо сместить кристаллы один относительно другого (без вращения), выведя границу из положения совпадающих узлов. При такой «релаксации» каждый атом остается в узле решетки своего кристалла. И хотя границы совпадающих узлов после указанного смещения зерен уже не существует, периодичность строения границы сохраняется и сохраняется сегмент повторяемости Р. 88

Зернограничные дислокации (ЗГД) стрелками отмечены две экстраплоскости Первоначально представления о ЗГД были введены для описания атомного меха низма зернограничного скольжения сме щения одного зерна относительно другого под действием напряжений. Граница зерна имеет периодическое строение. ЗГД отделяет ту часть межзеренной границы, где сдвиг уже прошел и восстановилось исходное периодическое строение границы, от той части, где он еще не начался. На рис. показана краевая ЗГД, являющаяся областью линей ного несовершенства на границе зерен вокруг края двух «лиш них» плоскостей в верхнем зерне. Вектор Бюргерса такой ЗГД лежит в плоскости границы, и ЗГД может скользить в этой плоскости. При скольжении ЗГД в каждый момент времени в сдвиге участвуют только те атомы, которые находятся в об ласти ядра дислокации. Продви жение одной дислокации по по верхности раздела соседних зе рен вызывает их взаимное сме щение на величину вектора Бюр герса ЗГД. Здесь полная анало гия со скольжением дислокаций внутри зерен, кото рые, для отличия от зерногра ничных, называют решеточными дислокациями 89

Малоугловые и высокоугловые границы 90

Уравнение Холла Петча Границы зерен препятствуют перемещению дислокаций и являются местом повышенной концентрации примесей, поэтому они оказывают существенное влияние на механические свойства металла. Под размером зерна принято понимать величину его среднего диаметра, определяемого в поперечном сечении. Размер зерна в металлах меняется в широких пределах – от нескольких микрометров до миллиметров. Размер зерна оценивается в баллах по специальной стандартизированной шкале и характеризуется числом зерен, приходящихся на 1 мм 2 поверхности шлифа, при увеличении х100. Процесс пластического течения и предел текучести зависят от длины свободного пробега дислокаций, определяемой размером зерна. Предел текучести σт связан с размером зерна d уравнением Холла – Петча: Чем мельче зерно, тем выше предел текучести и прочность металла. Одновременно при измельчении зерна увеличиваются пластичность и вязкость металла, что обусловлено более однородным строением мелкозернистого металла и меньшим количеством структурных несовершенств, способствующих образованию трещин. 91

Когерентные, полукогерентные и некогерентные границы когерентная граница – самая низкая поверхностная энергия и самая высокая упругая; некогерентная – самая высокая поверхностная энергия и самая низкая упругая 92

Двойники Ещё одним механизмом пластической деформации является двойникование. Как и скольжение, двойникование осуществляется за счет сдвига, однако в этом случае происходит сдвиг части кристалла в положение, соответствующее зеркальному отображению несдвинутой части. Двойникование, подобно скольжению, сопровождается прохождением дислокаций сквозь кристалл. При деформации двойникованием напряжение сдвига выше, чем при скольжении. Двойники обычно возникают тогда, когда скольжение по тем или иным причинам затруднено. Деформация двойникованием обычно наблюдается при низких температурах и высоких скоростях приложения нагрузки, так как в этих случаях для скольжения необходимо высокое напряжение сдвига. Двойники более характерны для металлов с ГП решеткой (Ті, Mg, Zn). 93

Микроструктура аустенитных зёрен с двойниками 94

Дефекты упаковки Это возможные отступления от закономерного расположения плотноупакованных слоев Появление дефекта упаковки не изменяет ни числа ближайших соседей атомов, ни расстояния до них. Но как показывает зонная теория, из за изменения в расположении следующих слоев (не ближайших) возрастает энергия электронного газа. Следовательно, с появлением дефекта упаковки связан избыток энергии, который называют энергией дефекта упаковки. Под ней подразумевают избыточную свободную энергию единицы площади дефекта упаковки. Теория показывает, что у одновалентных непереходных металлов (Сu, Ag, Au) энергия дефектов упаковки мала, а у многовалентных (Al, Mg, Zn, Cd) — велика. 95

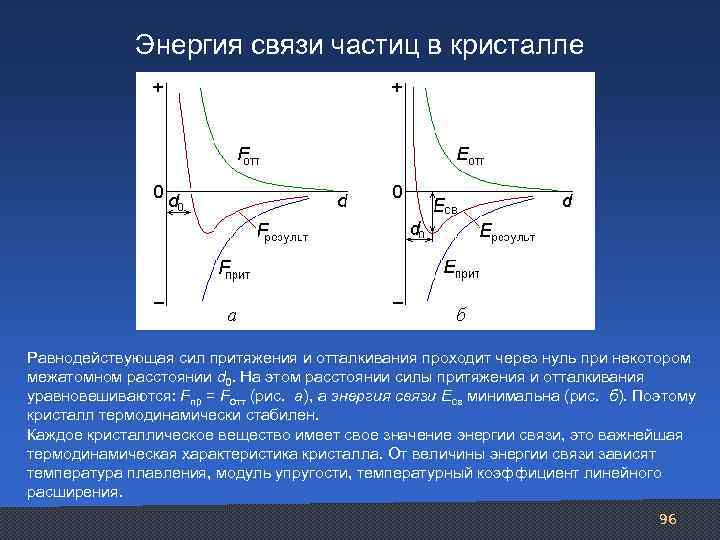
Энергия связи частиц в кристалле Равнодействующая сил притяжения и отталкивания проходит через нуль при некотором межатомном расстоянии d 0. На этом расстоянии силы притяжения и отталкивания уравновешиваются: Fпр = Fотт (рис. а), а энергия связи Eсв минимальна (рис. б). Поэтому кристалл термодинамически стабилен. Каждое кристаллическое вещество имеет свое значение энергии связи, это важнейшая термодинамическая характеристика кристалла. От величины энергии связи зависят температура плавления, модуль упругости, температурный коэффициент линейного расширения. 96

Энергия связи, тип кристалла Кристалл Ar CH 4 C Si. C Li. F Na. Cl Fe Na Есв, к. Дж/моль 7, 5 10 750 1180 1000 750 390 110 Тип связи молекулярная ковалентная ионная металлическая Тип кристалла молекулярный атомный ионный металлический 97

Молекулярная связь. Сила Ван дер Ваальса 98

Молекулярные кристаллы йод I 2 углекислый газ СО 2 В узлах решетки молекулы. Химическая связь между молекулами – силы Ван дер Ваальса между атомами в молекулах ковалентная полярная и неполярная. Свойства веществ: 1) малая твердость, прочность, 2) низкие Тпл, Ткип, 3) при комнатной Т обычно жидкость или газ, 4) высокая летучесть. Примеры: простые вещества (H 2, N 2, O 2, F 2, P 4, S 8, Ne, He), сложные вещества (СО 2, H 2 O, сахар С 12 H 22 O 11 и др. )

Ковалентная связь наиболее общий вид химической связи, возникающий за счет образования общей электронной пары. Виды ковалентной связи: полярная и неполярная. Механизмы ковалентной связи: обменный механизм каждый из взаимодействующих атомов поставляет по одному электрону донорно акцепторный механизм электронная пара передается в общее пользование одним атомом (донором) другому атому (акцептору). 100

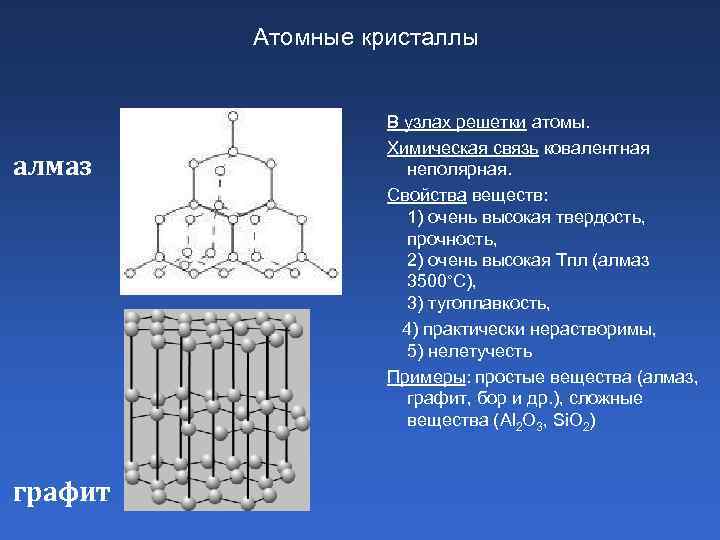
Атомные кристаллы алмаз графит В узлах решетки атомы. Химическая связь ковалентная неполярная. Свойства веществ: 1) очень высокая твердость, прочность, 2) очень высокая Тпл (алмаз 3500°С), 3) тугоплавкость, 4) практически нерастворимы, 5) нелетучесть Примеры: простые вещества (алмаз, графит, бор и др. ), сложные вещества (Al 2 O 3, Si. O 2)

Ионная связь, образующаяся за счет электростатического притяжения между разноименно заряженными ионами – катионами и анионами. Образовавшаяся электронная пара полностью принадлежит более электроотрицательному атому. Электроотрицательность условная величина, характеризующая способность атома в молекуле притягивать электроны. Полного перехода электронов при образовании ионной химической связи не происходит. Об этом свидетельствуют величины эффективных зарядов в соединениях. Ионная связь – образуется между металлом и неметаллом -1 +1 Na. Cl Na + Cl Na Cl Ненаправленность и ненасыщаемость: В ионном соединении каждый ион притягивает к себе независимо от направления неограниченное число противоположно заряженных ионов из за сил электростатического взаимодействия Взаимное отталкивание противоионов ограничивает их число в окружении каждого иона. 102

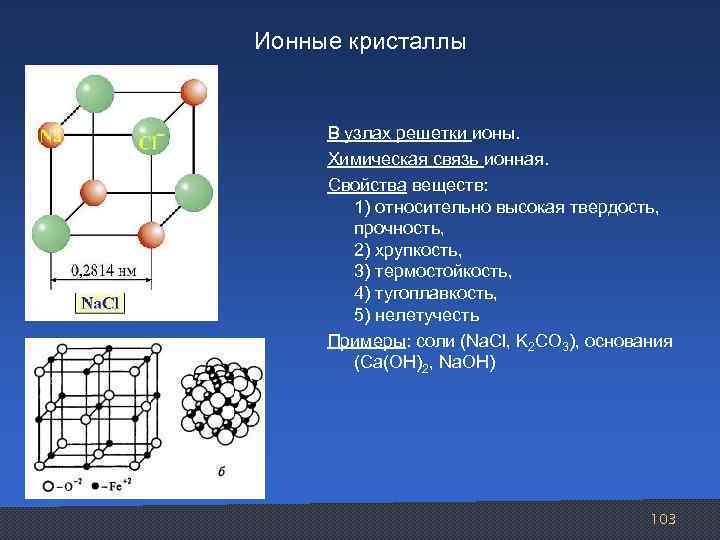
Ионные кристаллы В узлах решетки ионы. Химическая связь ионная. Свойства веществ: 1) относительно высокая твердость, прочность, 2) хрупкость, 3) термостойкость, 4) тугоплавкость, 5) нелетучесть Примеры: соли (Na. Cl, K 2 CO 3), основания (Ca(OH)2, Na. OH) 103

Металлическая связь возникает в результате движения свободных электронов, которые достаточно свободно движутся в решетке металлов, электростатически взаимодействуя с положительно заряженными ионами. Валентные электроны принадлежат одновременно всем атомам металла, свободно перемещаясь по всему кристаллу, образуя единое электронное облако ( «электронный газ» ). Электроны обладают свойствами волны, они «размазаны» по всему объёму металла. 104

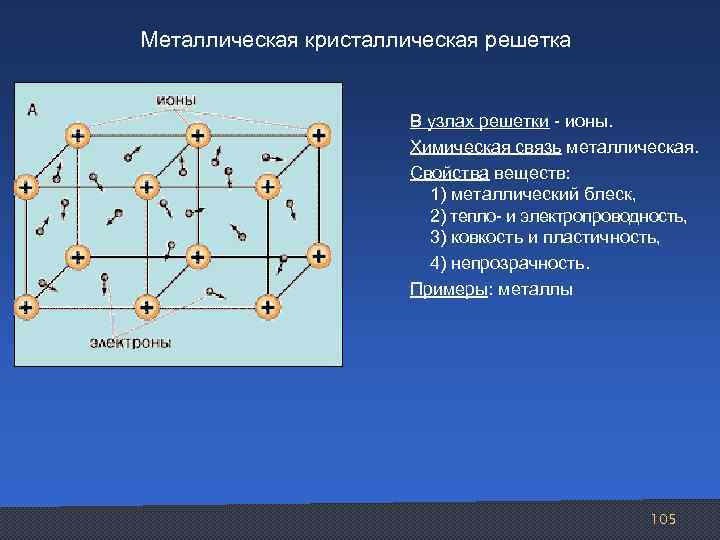
Металлическая кристаллическая решетка В узлах решетки ионы. Химическая связь металлическая. Свойства веществ: 1) металлический блеск, 2) тепло и электропроводность, 3) ковкость и пластичность, 4) непрозрачность. Примеры: металлы 105

Полиморфизм – явление существования одного химического элемента в разных кристаллических модификациях. Устойчивость той или иной кристаллической формы при данных внешних условиях определяется величиной свободной энергии модификации. Полиморфизм обнаружен для 37 химических элементов. 106

Полиморфизм железа 107

Влияние давления на полиморфизм железа 108

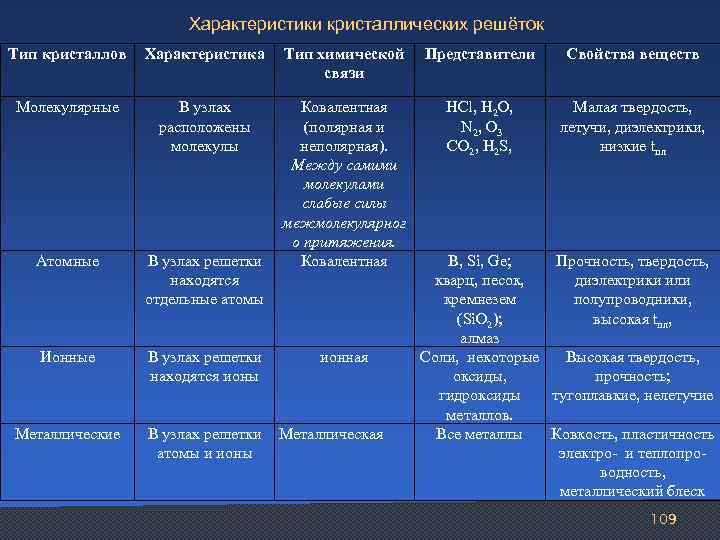
Характеристики кристаллических решёток Тип кристаллов Характеристика Тип химической связи Представители Свойства веществ Молекулярные В узлах расположены молекулы HCl, H 2 O, N 2, O 3 CO 2, H 2 S, Малая твердость, летучи, диэлектрики, низкие tпл Атомные В узлах решетки находятся отдельные атомы Ковалентная (полярная и неполярная). Между самими молекулами слабые силы межмолекулярног о притяжения. Ковалентная Ионные В узлах решетки находятся ионы Металлические В узлах решетки атомы и ионы ионная Металлическая B, Si, Ge; Прочность, твердость, кварц, песок, диэлектрики или кремнезем полупроводники, (Si. O 2); высокая tпл, алмаз Соли, некоторые Высокая твердость, оксиды, прочность; гидроксиды тугоплавкие, нелетучие металлов. Все металлы Ковкость, пластичность электро- и теплопроводность, металлический блеск 109

Основы дислокационной теории 110

Вектор Бюргерса Если обвести контуром несколько дислокаций, сливающихся и перекрещивающихся в одной зоне, то можно получить вектор Бюргерса, соответствующий сумме векторов Бюргерса каждой дислокации. 111

Вектор Бюргерса винтовой дислокации 112

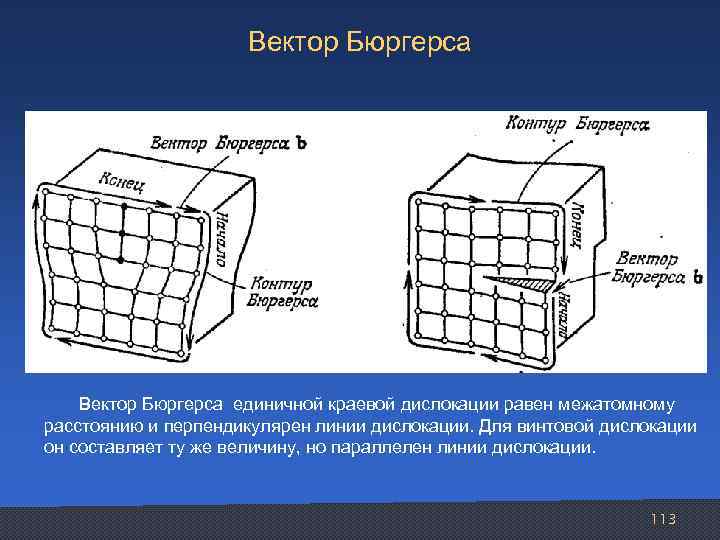
Вектор Бюргерса Вектор Бюргерса единичной краевой дислокации равен межатомному расстоянию и перпендикулярен линии дислокации. Для винтовой дислокации он составляет ту же величину, но параллелен линии дислокации. 113

Вектор Бюргерса: • кратен вектору трансляции кристаллической структуры (решётки Бравэ); • перпендикулярен линии краевой дислокации, параллелен линии винтовой дислокации; • любой дислокации можно представить как сумму краевой и винтовой компонент; • имеет постоянное значение и не меняется вдоль линии дислокации. 114

• Скачок вектора Бюргерса в некоторой точке означает ветвление дислокации в этой точке • При разветвлении дислокационной линии суммарная величина вектора Бюргерса не меняется 115

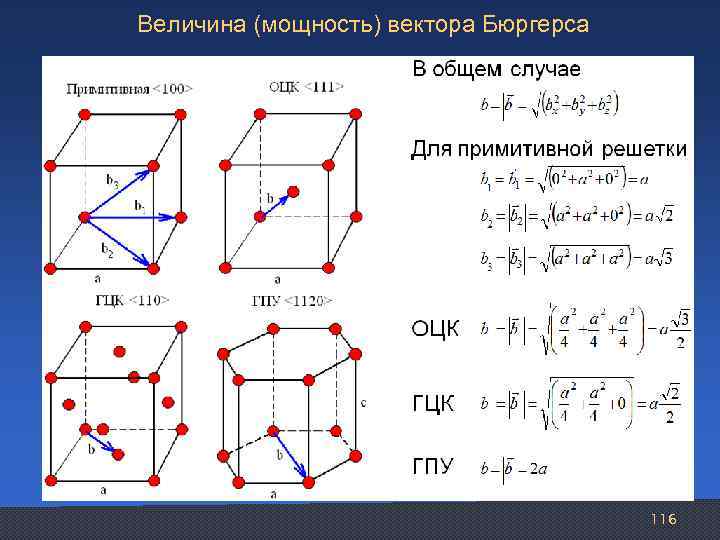
Величина (мощность) вектора Бюргерса 116

Энергия дислокации τ L b ядро R R τ L G модуль сдвига, b вектор Бюргерса, n- коэффициент Пуассона, R – радиус зоны, ro – радиус ядра дислокации 117

В бесконечно большом монокристалле Eд→∞, так как R →∞. В реальных поликристаллах r 0~10 нм, R не более размера зерна (~1 1000 мкм). Тогда множитель a = (1/4 p) ln(R/r 0) ~ 0, 5 1. Окончательно энергия образования дислокации: Энергия единицы ее длины: 118

Энергия движущейся дислокации v – скорость дислокации, с – скорость звука в материале. Если v мала, то Eдв Ед. При большой v Eдв >Ед ; v всегда меньше с. 119

Термодинамика дислокации • Вклад энергии ядра дислокации в общую энергию близок к 10 %. Таким образом, основной вклад в энергию дислокаций вносит поле дальнодействующих упругих напряжений. • Энергия дислокации длиной в один параметр решётки значительна: Eд ~ 0. 5 Gb 3 ~3 э. В. • Система стремится к состоянию с минимальной свободной энергией: ΔG = ΔH - TΔS • Образование дислокаций увеличивает S (в соответствии с S = k ln W) и H за счет Eд. При этом ΔH = Eд всегда >ΔS. Поэтому дислокации термодинамически неравновесны, т. е. они не могут возникнуть самопроизвольно в результате термических флуктуаций, как вакансии. • В реальных кристаллах дислокации есть всегда, потому что равновесное состояние практически недостижимо, т. к. для этого необходимо охлаждать материал при кристаллизации с бесконечно малой скоростью. 120

Сила, действующая на дислокацию Работа сдвига A=Pb, сила P = t. F = t l l. 1 2 Тогда A = tl l b Пусть f – сила, действующая на единицу длины дислокации. Тогда P = fl 1 и A = fl 1 l 2 Сравнивая 1) и 2), получим 1 2 f = tb 1) 2) 121

Выгибание дислокации На участке l сила F = tb l 1) Линейное натяжение препятствует выгибанию: Fн = 2 Tsin f/2, sin f/2, f = l/r Тогда 2) Сравнивая 1) и 2), получим напряжение для напряжения выгибания дислокации в дугу: 122

Скольжение дислокаций Пластическая деформация металлов и сплавов при Т < (0, 7 – 0, 8)Тпл осуществляется главным образом за счёт скольжения дислокаций, поэтому прочность металла напрямую зависит от лёгкости движения дислокаций. Движению дислокаций в кристалле препятствуют: силы Пайерлса – Набарро; другие дислокации; примесные атомы. 123

Скольжение дислокаций Краевая дислокация имеет единственную плоскость скольжения. L b b Любая плоскость, содержащая линию дислокации, является плоскостью скольжения для винтовой дислокации. L 124

Скольжение краевых дислокаций b Плоскость скольжения должна содержать линию дислокации и вектор Бюргерса. Скольжение дислокаций идёт скачками из одного устойчивого положения к другому. При элементарном перескоке происходит разрыв определённого количества атомных связей в ядре дислокации, что требует затрат энергии на преодоление энергетического барьера Пайерлса (UП), следовательно, для движения дислокации необходимо внешнее напряжение, которое и совершит эту работу. 125

Сила (барьер) Пайерлса Набарро Барьер Пайерлса – Набарро определяет сопротивление кристаллической решётки скольжению. q=1 для винтовой дислокации, q=1 n для краевой дислокации Чем меньше вектор Бюргерса b и больше межплоскостное расстояние d, тем меньше барьер Пайерлса – Набарро. d/b=1 ПН=4 10 -3 G d/b=1. 5 ПН=1. 5 10 -4 G 126

Анализ силы ПН 127

Системы скольжения в кристаллах Теория дислокаций показывает, что для данной кристаллической решётки должно наблюдаться лишь несколько плоскостей и направлений скольжения, которые образуют системы скольжения в кристалле. Сопротивление скольжению минимально для дислокаций с наименьшими векторами Бюргерса и в плоскостях с максимальным расстоянием между ними. Такими плоскостями и направлениями являются плотноупакованные плоскости и направления с наименьшими индексами {hkl} и <mnp>. 128

Скольжение дислокаций Наблюдаемые системы скольжения – Дислокация должна иметь наименьший вектор Бюргерса т. к. E ~Gb 2. b – минимальный вектор трансляции – Плоскость скольжения должна иметь максимальное значение межплоскостного расстояния - d. Плоскости скольжения – плоскости, имеющие максимальную плотность узлов решётки 129

Системы скольжения в ГЦК Минимальный вектор трансляции а/2 [110] Плоскости с максимальной плотностью узлов и максимальным d {111} В ГЦК решётке 4 различных плоскости {111}, в каждой содержится 3 вектора а/2 [110], поэтому всего 4 х3 =12 систем скольжения совокупности {111}<110>. 130

Системы скольжения в ОЦК Минимальный вектор трансляции а/2 [111] Плоскости с максимальной плотностью узлов и максимальным d {110} В ОЦК решётке 6 различных плоскости {110}, в каждой содержится 2 вектора а/2 [111], поэтому всего 6 х2=12 систем скольжения совокупности {110}<111>. Имеется также вторая совокупность {112}<111>, связанная с наличием в ОЦК кристаллах дефектов упаковки, расположенных в плоскостях {112}. Эти плоскости являются плоскостями скольжения для частичных дислокаций. 131

Консервативное движение краевой дислокации (скольжение) t b t Под действием t происходит смещение атомов на расстояния менее межатомных, разрыв и образование межатомных связей вдоль линии, перпендикулярной t и лежащей в плоскости скольжения. Образуется экстраплоскость, край которой под действием t перемещается сквозь кристалл по «эстафете» и выходит на противоположной стороне. Движение консервативное: • дислокация не выходит из плоскости скольжения; • нет переноса массы, т. к. сама экстраплоскость не движется; • смещение атомов на расстояния менее межатомных. 132

Консервативное движение винтовой дислокации (поперечное скольжение) Винтовая дислокация относительно легко переходит из одной атомной плоскости скольжения в другую, что объясняется цилиндрической симметрией расположения атомов вокруг линии дислокации. Этот процесс назван поперечным скольжением. Смена плоскости скольжения происходит из за наличия препятствий (барьеров) в первоначальной плоскости скольжения или изменения направления касательных напряжений. Так, на рисунке показано двойное поперечное скольжение: из первоначальной плоскости А дислокация перешла в плоскость В и вновь в плоскость С, параллельную первоначальной плоскости скольжения А. 133

Неконсервативное движение краевой дислокации (переползание) При повышенных температурах увеличивается скорость диффузии и в решётке появляются дополнительные вакансии сверх равновесной концентрации, Активизируется другой механизм движения дислокаций за счёт диффузии атомов и вакансий из объема кристалла к краю экстраплоскости. Движение перпендикулярно плоскости скольжения, образуются устойчивые пороги, которые также являются краевыми дислокациями. Движение неконсервативное. 134

Положительное переползание дислокации Дислокация – сток вакансий Перемещение дислокации вакансия 135

Отрицательное переползание дислокации Дислокация – источник вакансий Перемещение дислокации вакансия 136

Равновесное количество порогов 137

Полная и частичная дислокация • 138

Дислокации Шокли 139

Дислокации Шокли При скольжении частичная дислокация смещает атомы в «неправильные» положения и оставляет за собой дефект упаковки. При прохождении следующей частичной дислокации происходит обратный процесс и дефект упаковки исчезает. Вектор Бюргерса дислокации Шокли лежит в плоскости нарушения. 140

Кристаллизация – процесс образования кристаллов из жидкой фазы (затвердевание металлов и сплавов). Обратный процесс – плавление. Кристаллизация подчиняется общим закономерностям, присущим фазовым превращениям, в том числе протекающим в твёрдом состоянии. Свободная энергия G – часть полной внутренней энергии вещества, которая может меняться при изменении внешних условий (температуре и давлении). Самопроизвольно процессы идут только в сторону уменьшения свободной энергии. Устойчивой при данных температуре и давлении будет фаза с меньшей свободной энергией. 141

Метод термического анализа 142

Движущая сила процесса кристаллизации – разность свободных энергий Δ G, возникающая при переохлаждении сплава. Δ Т – степень переохлаждения. Т 1 ТS Т 2 G ΔG FТ FЖ ΔT Ткр Ттеор Температура, °С 143

Схема кристаллизации металла 1. Образование центров кристаллизации 2. Рост кристаллов 144

Модели расположения атомов в фазах а б в а и б – жидкой; в – кристаллической 145

146

Схема макроструктур слитков Схема а б в а – три зоны кристаллов (1 – мелкие равноосные; 2 – столбчатые; 3 – равноосные); б – столбчатые кристаллы; в – равноосные кристаллы Материаловедение ( «Машиностроение» ). Лекция 2 147

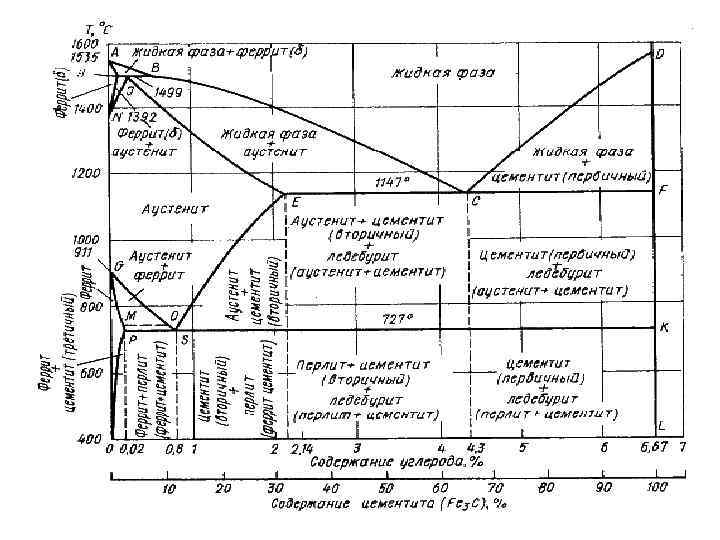
Теория сплавов и диаграммы состояния Компоненты – химические элементы, образующие сплав (иногда химические соединения). Фаза – однородная составная часть сплава, имеющая одинаковый химический состав, кристаллическое строение и отделённая от других частей поверхностью раздела: 1. Твёрдые растворы. 2. Промежуточные фазы. Структурная составляющая – внешний вид фазы или совокупности фаз: 1. Однофазная. 2. Многофазная Сплав – термодинамическая система, представляющая собой совокупность фаз, находящихся в одном из трёх возможных энергетических состояний: 1. Неравновесное. 2. Метастабильное. 3. Равновесное. Диаграмма состояния – наглядное графическое изображение совокупности фаз в зависимости от температуры и концентрации компонентов: 1. Метастабильная. 2. Стабильная. Правило фаз: С = К – Ф + 1 С – число степеней свободы – число внешних и внутренних факторов, которое можно изменять без изменения числа фаз в системе. 148

Микроструктуры углеродистых доэвтектоидных сталей и схемы их зарисовки а б в а – техническое железо; б – сталь 45; в – сталь У 8

Сталь 40 (0, 4%С, структура – Ф+П) 154

155

Сталь У 8 (0, 8%С) П пл. х150 П зерн. х150 х600 156

Сталь У 10 (1, 0%С, структура – П+Ц) 157

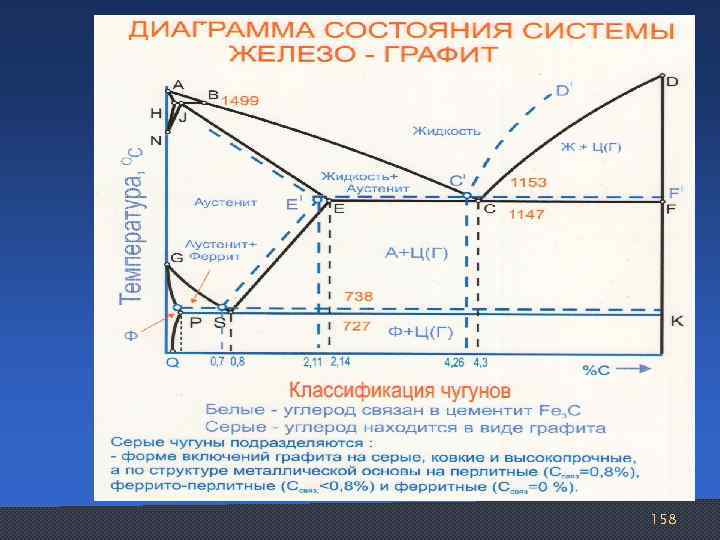
158

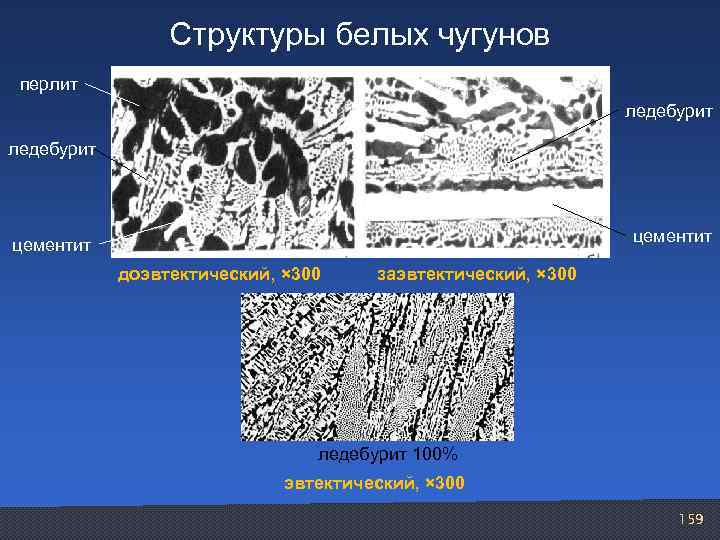
Структуры белых чугунов перлит ледебурит цементит доэвтектический, × 300 заэвтектический, × 300 ледебурит 100% эвтектический, × 300 159

Внешний вид графитных включений и схемы их зарисовки а а – пластинчатый; б б – шаровидный в в – хлопьевидный 160

161

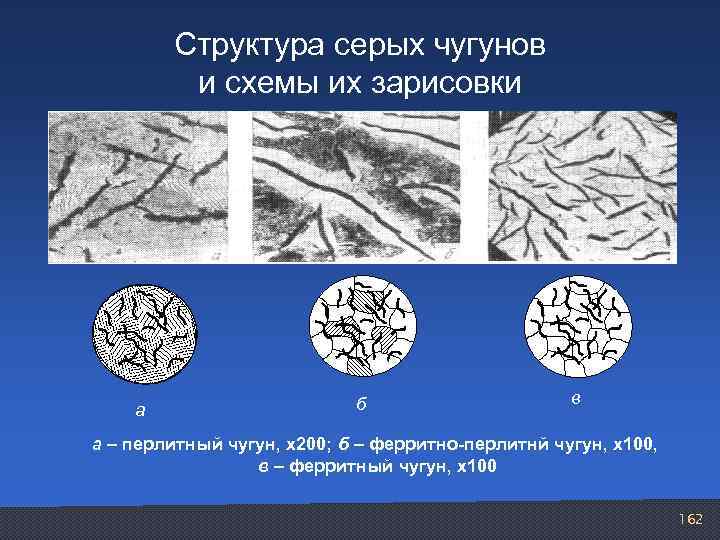
Структура серых чугунов и схемы их зарисовки а б в а – перлитный чугун, х200; б – ферритно-перлитнй чугун, х100, в – ферритный чугун, х100 162

Механические свойства некоторых серых чугунов ( ГОСТ 1412 85) sв, МПа d, % НВ Структура металлической основы СЧ 15 150 163 229 Ф СЧ 25 250 180 250 Ф+П СЧ 40 400 207 285 П СЧ 45 450 229 2890 П Чугун 163

164

Структуры ковких чугунов и схемы их зарисовки а б в а – ферритный ковкий чугун, × 200; б – ферритно-перлитный ковкий чугун, × 200; в – перлитный ковкий чугун, × 200 165

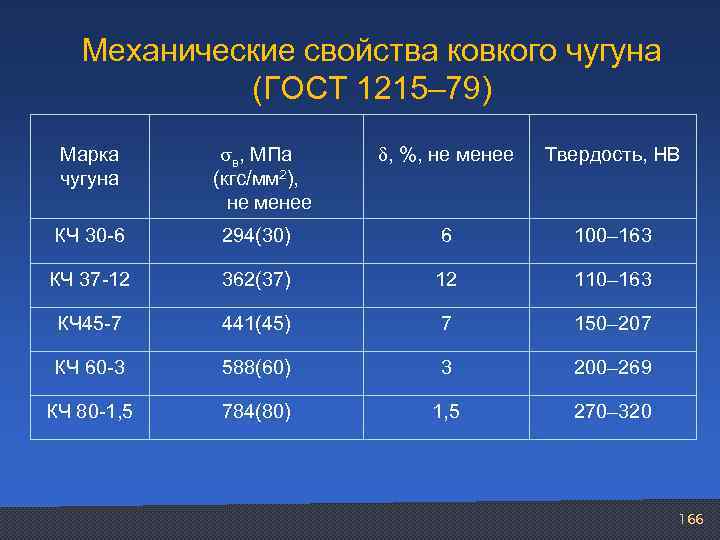
Механические свойства ковкого чугуна (ГОСТ 1215– 79) Марка чугуна в, МПа (кгс/мм 2), не менее , %, не менее Твердость, НВ КЧ 30 6 294(30) 6 100– 163 КЧ 37 12 362(37) 12 110– 163 КЧ 45 7 441(45) 7 150– 207 КЧ 60 3 588(60) 3 200– 269 КЧ 80 1, 5 784(80) 1, 5 270– 320 166

167

Структуры высокопрочных чугунов и схемы их зарисовки а б а – высокопрочный чугун на ферритной основе; б – высокопрочный чугун на ферритно-перлитной основе 168

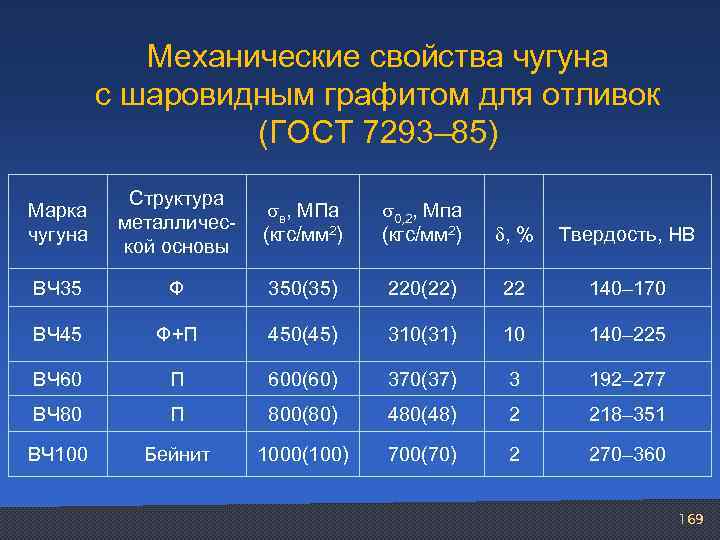
Механические свойства чугуна с шаровидным графитом для отливок (ГОСТ 7293– 85) Марка чугуна Структура металличес кой основы в, МПа (кгс/мм 2) 0, 2, Мпа (кгс/мм 2) , % Твердость, НВ ВЧ 35 Ф 350(35) 220(22) 22 140– 170 ВЧ 45 Ф+П 450(45) 310(31) 10 140– 225 ВЧ 60 П 600(60) 370(37) 3 192– 277 ВЧ 80 П 800(80) 480(48) 2 218– 351 ВЧ 100 Бейнит 1000(100) 700(70) 2 270– 360 169

Твёрдость чугунов не зависит от формы графита, а определяется типом металлической основы Рост твёрдости 170