Фазовые Диаграммы.ppt
- Количество слайдов: 43

Фазовые диаграммы Бокштейн Б. С. Долгополов Н. А. Родин А. О. Похвиснев Ю. В. кафедра физической химии 2006 г.

ФАЗА (Ф) – однородная часть неоднородной системы, отделена от других частей системы поверхностью раздела, имеет определенный химический состав и термодинамические свойства КОМПОНЕНТ (К) – индивидуальное вещество, составляющее системы Число независимых компонентов – это число таких веществ за вычетом числа связывающих их уравнений Пример – система: CO, CO 2, Fe и Fe. O – 5 веществ, но веществ 2 Fe + O 2 = 2 Fe. O и Fe. O + CO = Fe + CO 2 поэтому число компонентов К = 5 – 2 = 3 ЧИСЛО СТЕПЕНЕЙ СВОБОДЫ (C) – число независимых параметров, задание которых определяет состояние системы, или число параметров, которые можно менять, не меняя фазового состояния системы

ПРАВИЛО ФАЗ ГИББСА (1883 «О равновесии гетерогенных веществ) С = число параметров минус число связывающих эти параметры уравнений (независимых параметров) Имеем К компонентов и Ф фаз Число параметров: Число уравнений: КФ (концентрации) + 2 (Т, р) m 1 I = m 1 II = … = m 1 Ф m 2 I = m 2 II = … = m 2 Ф …………… m. КI = m. КII = … = m. КФ С = КФ + 2 – К(Ф-1) – Ф С=К+2 -Ф К(Ф-1) плюс Ф уравнений состояния

ПРАВИЛО ФАЗ ГИББСА (1883 «О равновесии гетерогенных веществ) С=К+2 -Ф т. к. С ≥ 0, то Ф ≤ К + 2, т. е. при К=1 К=2 Ф≤ 3 Ф ≤ 4 и т. д. С = 0 – новариантное равновесие (ничего нельзя менять); С = 1 – моновариантное равновесие (можно менять один параметр)
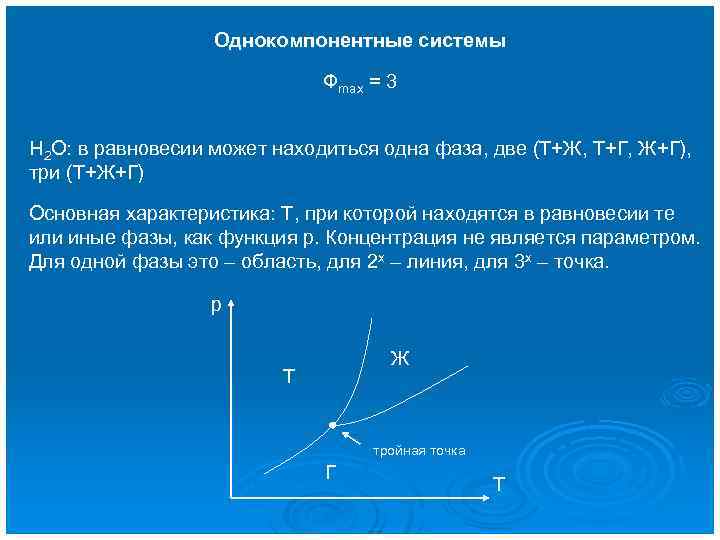
Однокомпонентные системы Фmax = 3 H 2 O: в равновесии может находиться одна фаза, две (Т+Ж, Т+Г, Ж+Г), три (Т+Ж+Г) Основная характеристика: Т, при которой находятся в равновесии те или иные фазы, как функция р. Концентрация не является параметром. Для одной фазы это – область, для 2 х – линия, для 3 х – точка. р Ж Т тройная точка Г Т

Однокомпонентные системы Фmax = 3 Фазовые переходы первого рода (агрегатные и аллотропические превращения: плавление, испарение, Fe → Feg и т. д. ) Для них: DH ≠ 0 и DV ≠ 0. Вдоль линий равновесия GI (T, p) = GII (T, p) Возьмем от GI и GII полные производные по Т (или по р): уравнение Клаузиуса-Клапейрона
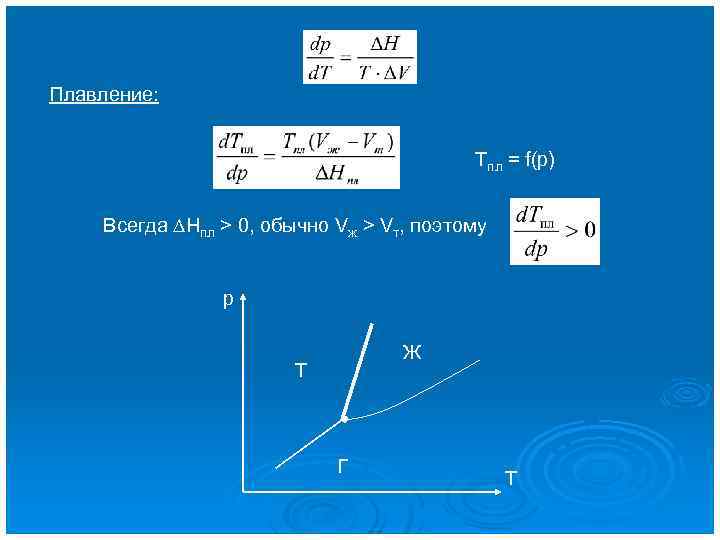
Плавление: Tпл = f(p) Всегда DHпл > 0, обычно Vж > Vт, поэтому р Ж Т Г Т
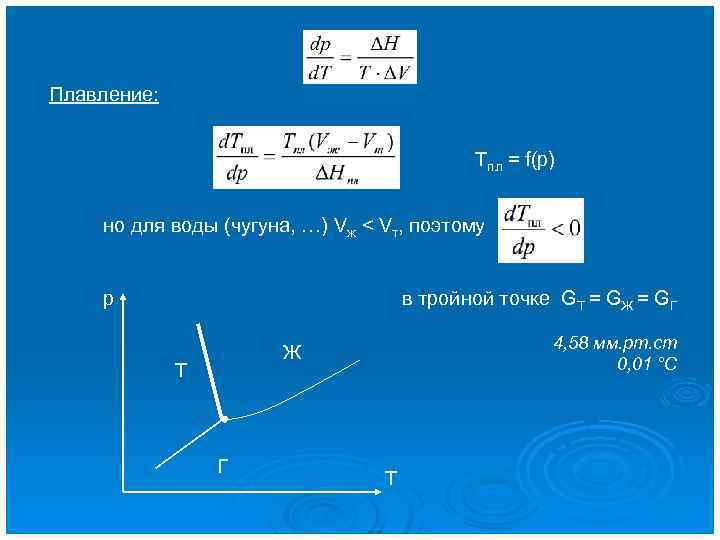
Плавление: Tпл = f(p) но для воды (чугуна, …) Vж < Vт, поэтому р в тройной точке GТ = GЖ = GГ 4, 58 мм. рт. ст 0, 01 °С Ж Т Г Т
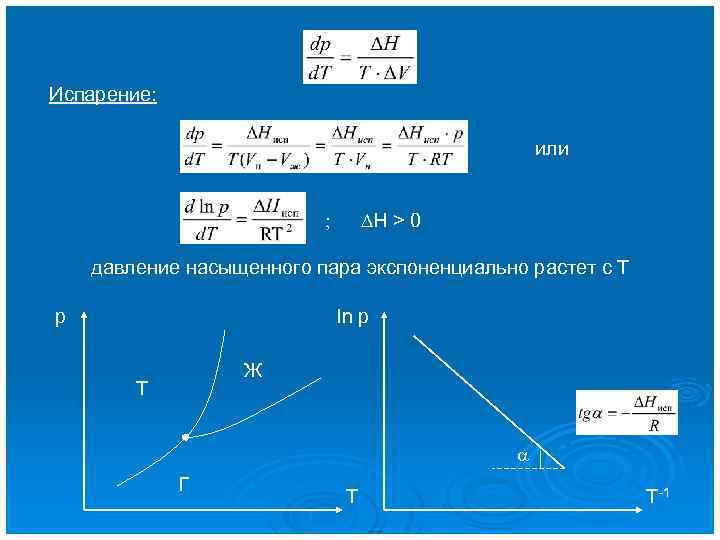
Испарение: или ; DH > 0 давление насыщенного пара экспоненциально растет с Т р ln р Ж Т Г Т Т-1

Что такое фазовые диаграммы? Фазовые диаграммы – это способ графического представления состояния равновесия систем, с указанием типа фаз и их параметров (температура, давление и состав), которые могут находиться в состоянии равновесия в системе.

Основные замечания Ø Для конденсированных систем свойства фаз слабо зависят от давления. Поэтому С=К-Ф+1 Ø Если в системе только 2 компонента, то К=2 и максимальное число фаз Ф макс=2+1=3. Итак в системе может быть 1, 2 или 3 фазы Ø Координаты для построения диаграмм: температура - состав. Наиболее удобным способом выражения состава являются мольные (или массовые) доли, так как: - не зависят от температуры - имеют ограниченную область значений от 0 до 1 (или от 0 до 100 в процентах) - позволяют легко перейти от концентрации одного компонента к концентрации другого - в этих единицах можно выбирать как состав системы целиком, так и состав каждой из фаз

С помощью фазовых диаграмм можно предсказать: Ø Какие фазы находятся в равновесии в сплаве Ø Какой состав имеют фазы в равновесии Ø Какое количество (масса) фаз будет в сплаве Ø Какие превращения произойдут в результате термической обработки, нагрева или охлаждения Можно предсказывать свойства получаемого материала и давать рекомендации по усовершенствованию процессов термической обработки и легирования материалов для обеспечения заданных свойств.
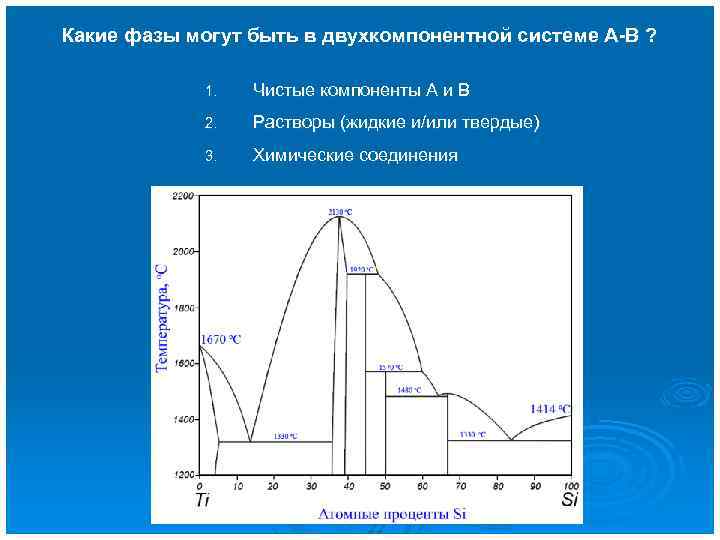
Какие фазы могут быть в двухкомпонентной системе А-В ? 1. Чистые компоненты А и В 2. Растворы (жидкие и/или твердые) 3. Химические соединения

Типы равновесий: 1) Возможно образование жидких растворов любой концентрации. В твердом состоянии вещества не растворяются друг в друге. 2) Возможно образование жидких растворов любой концентрации. Возможно образование твердых растворов любой концентрации. 3) Возможно образование жидких растворов любой концентрации. Растворимость в твердом состояния ограничена. 4) Имеются твердые химические соединения. Растворимость в твердом состоянии ограничена или отсутствует. 5) Ограниченная растворимость в жидком состоянии.

Диаграммы систем с полной растворимостью в жидком состоянии и отсутствием растворимости в твердом Закон понижения температуры замерзания: Если примесь не растворяется в твердом состоянии, то температура замерзания раствора ниже, чем температура замерзания чистого растворителя. Для совершенного раствора задача сводится к решению системы уравнений:
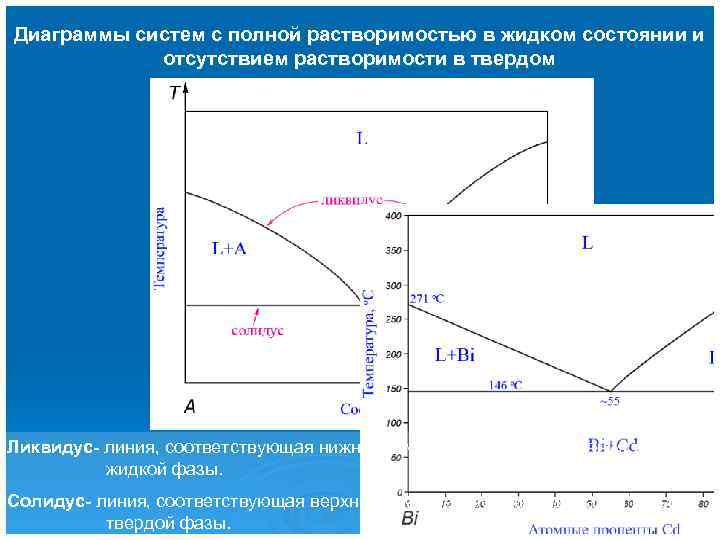
Диаграммы систем с полной растворимостью в жидком состоянии и отсутствием растворимости в твердом Ликвидус- линия, соответствующая нижней температуре существования только жидкой фазы. Солидус- линия, соответствующая верхней температуре существования только твердой фазы.
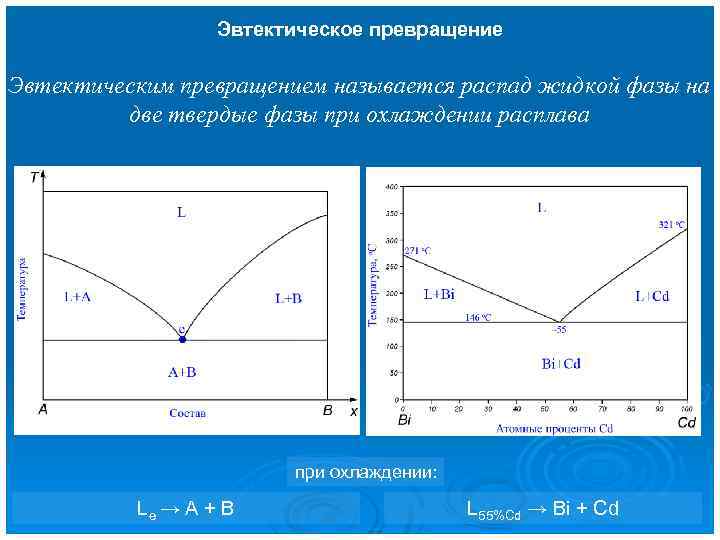
Эвтектическое превращение Эвтектическим превращением называется распад жидкой фазы на две твердые фазы при охлаждении расплава при охлаждении: Le → A + B L 55%Cd → Bi + Cd
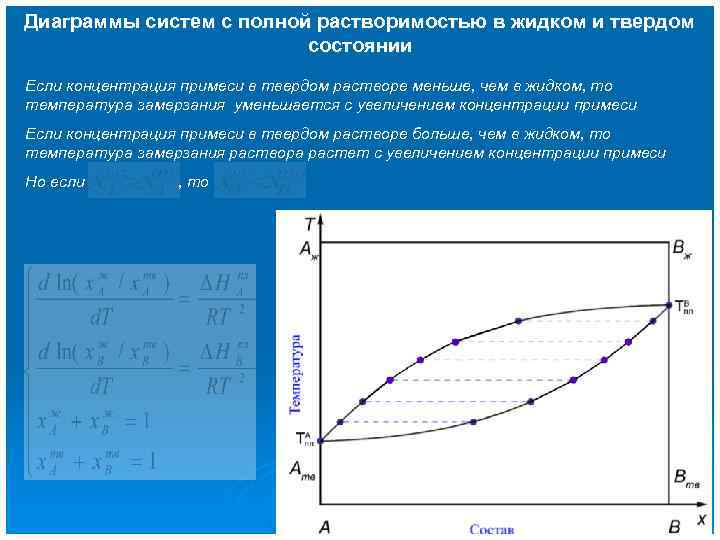
Диаграммы систем с полной растворимостью в жидком и твердом состоянии Если концентрация примеси в твердом растворе меньше, чем в жидком, то температура замерзания уменьшается с увеличением концентрации примеси Если концентрация примеси в твердом растворе больше, чем в жидком, то температура замерзания раствора растет с увеличением концентрации примеси Но если , то
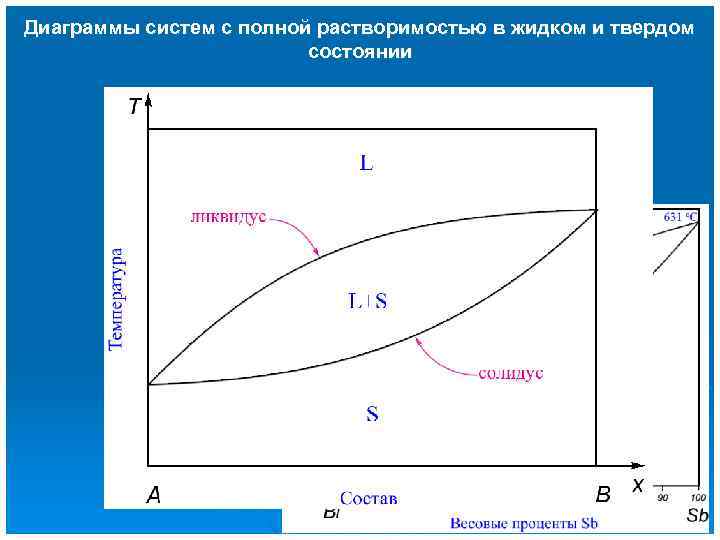
Диаграммы систем с полной растворимостью в жидком и твердом состоянии

Диаграммы систем с полной растворимостью в жидком и твердом состоянии В неидеальных растворах возможно понижение/повышение температуры с обеих сторон В точке минимума (максимума) составы твердой и жидкой фаз совпадают
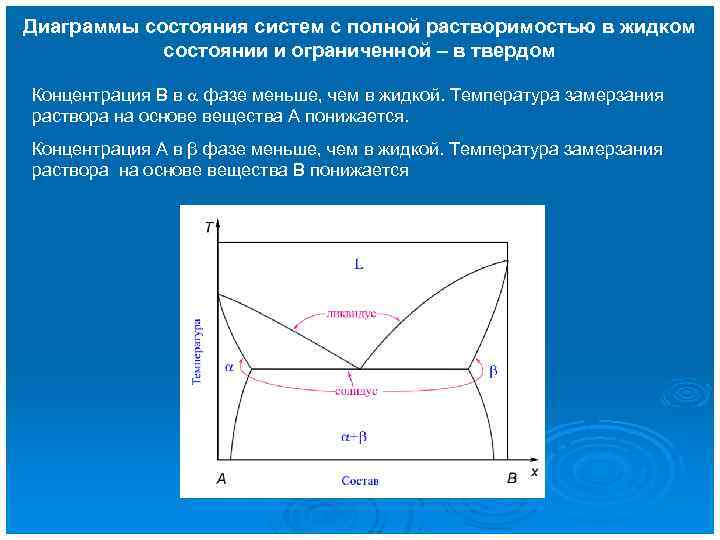
Диаграммы состояния систем с полной растворимостью в жидком состоянии и ограниченной – в твердом Концентрация В в фазе меньше, чем в жидкой. Температура замерзания раствора на основе вещества А понижается. Концентрация А в β фазе меньше, чем в жидкой. Температура замерзания раствора на основе вещества В понижается
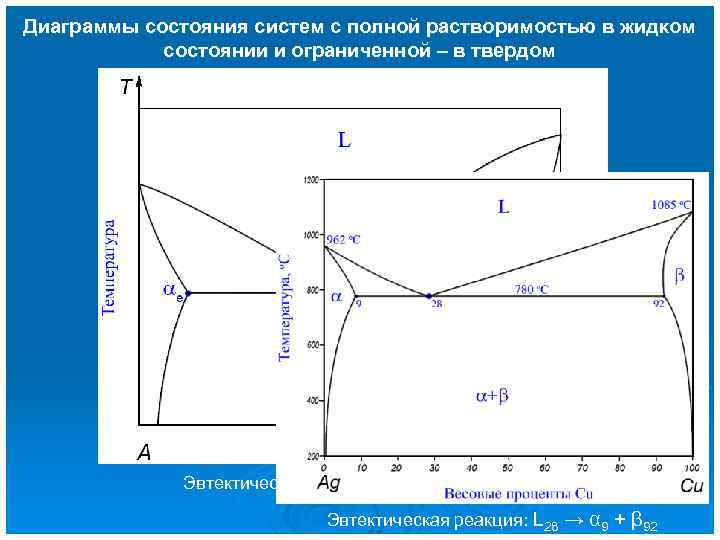
Диаграммы состояния систем с полной растворимостью в жидком состоянии и ограниченной – в твердом Эвтектическая реакция: Le → αe + β e Эвтектическая реакция: L 28 → α 9 + β 92

Диаграммы состояния систем с полной растворимостью в жидком состоянии и ограниченной – в твердом Концентрация В в фазе меньше, чем в жидкой. Температура замерзания раствора на основе вещества А понижается. Концентрация А в β фазе больше, чем в жидкой. Температура замерзания раствора на основе вещества В повышается
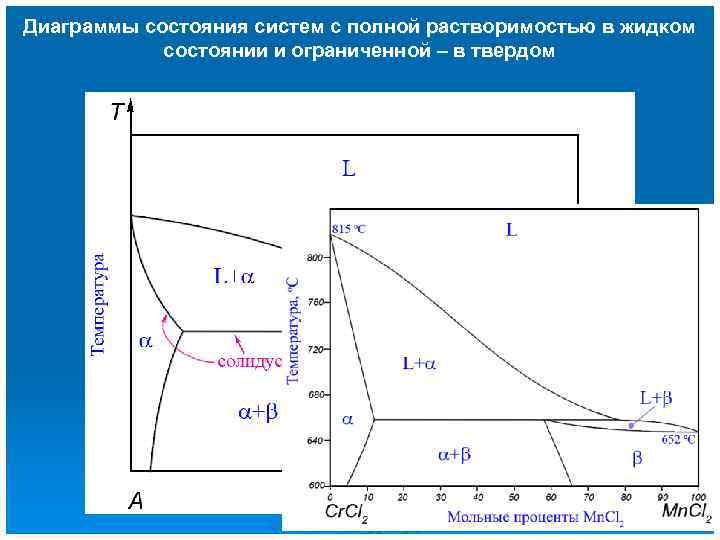
Диаграммы состояния систем с полной растворимостью в жидком состоянии и ограниченной – в твердом

Перитектическое превращение Перитектическим превращением называется реакция взаимодействия жидкой фазы c одной твердой фазой, приводящая к образованию другой твердой фазы. при охлаждении: Lp + αp → β p L 78 + α 10 → β 59
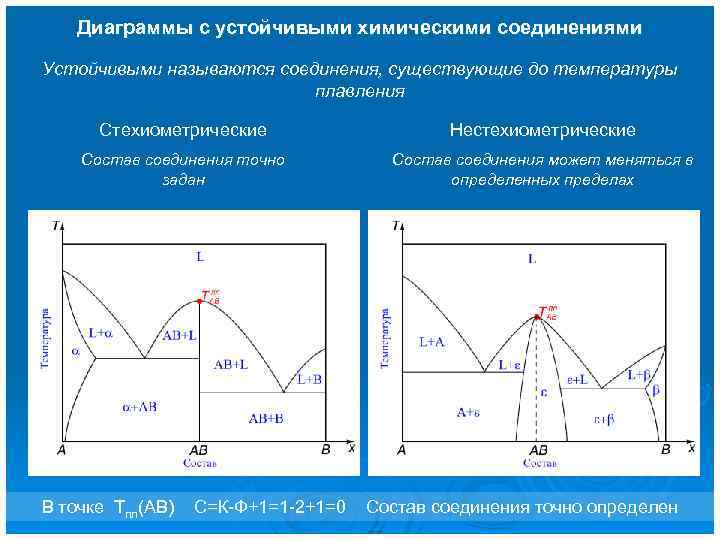
Диаграммы с устойчивыми химическими соединениями Устойчивыми называются соединения, существующие до температуры плавления Стехиометрические Нестехиометрические Состав соединения точно задан Состав соединения может меняться в определенных пределах В точке Тпл(AB) С=К-Ф+1=1 -2+1=0 Состав соединения точно определен

Диаграммы с неустойчивыми химическими соединениями Неустойчивыми называются соединения, распадающиеся при нагреве на две фазы разного состава Стехиометрические Нестехиометрические при охлаждении: Lp + αp → AB Lp + βp → εAB
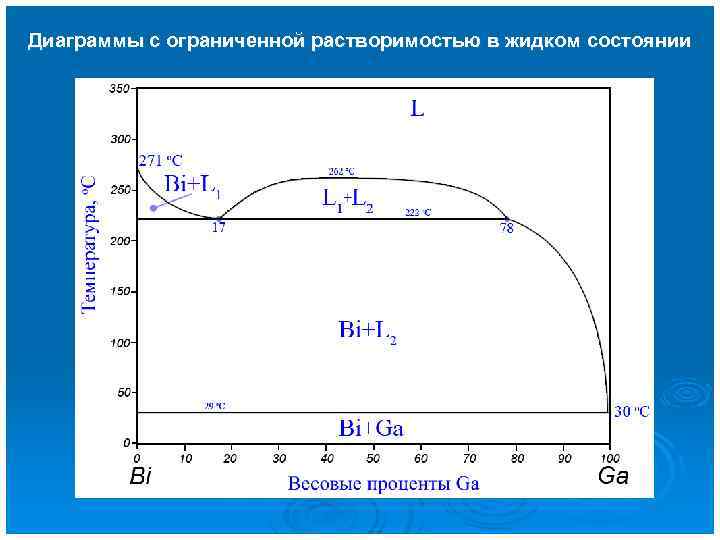
Диаграммы с ограниченной растворимостью в жидком состоянии
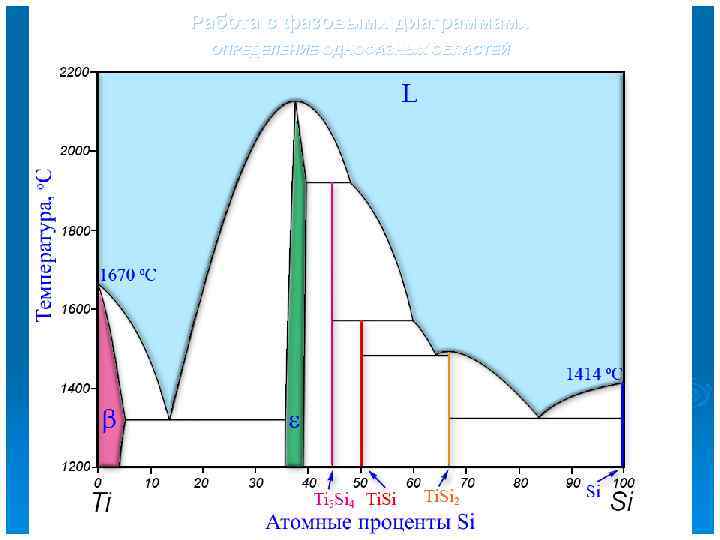
Работа с фазовыми диаграммами ОПРЕДЕЛЕНИЕ ОДНОФАЗНЫХ ОБЛАСТЕЙ
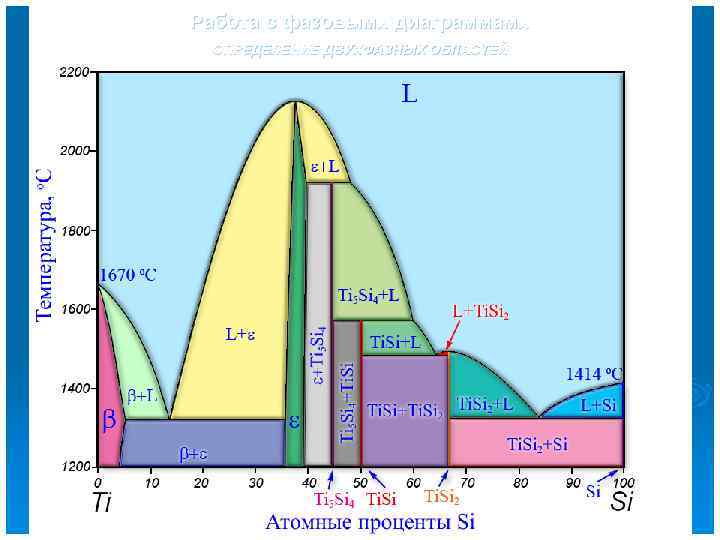
Работа с фазовыми диаграммами ОПРЕДЕЛЕНИЕ ДВУХФАЗНЫХ ОБЛАСТЕЙ
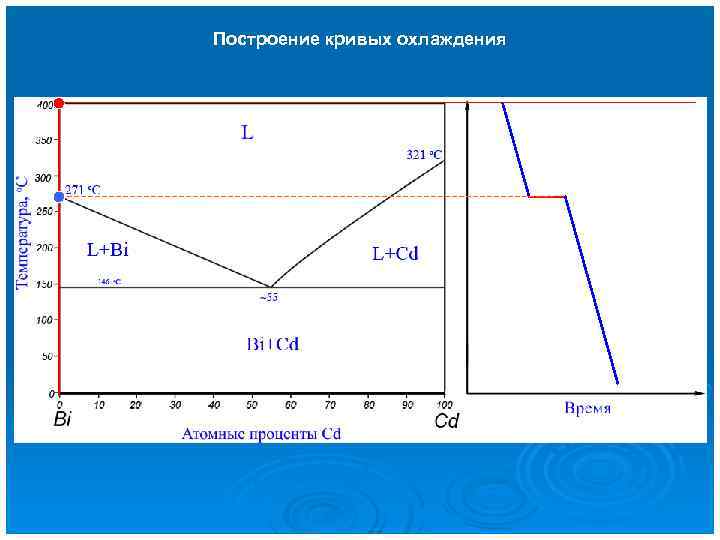
Построение кривых охлаждения
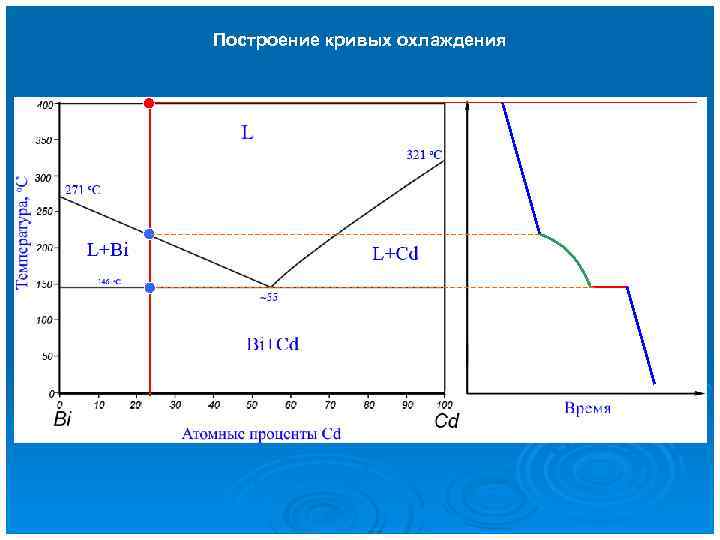
Построение кривых охлаждения
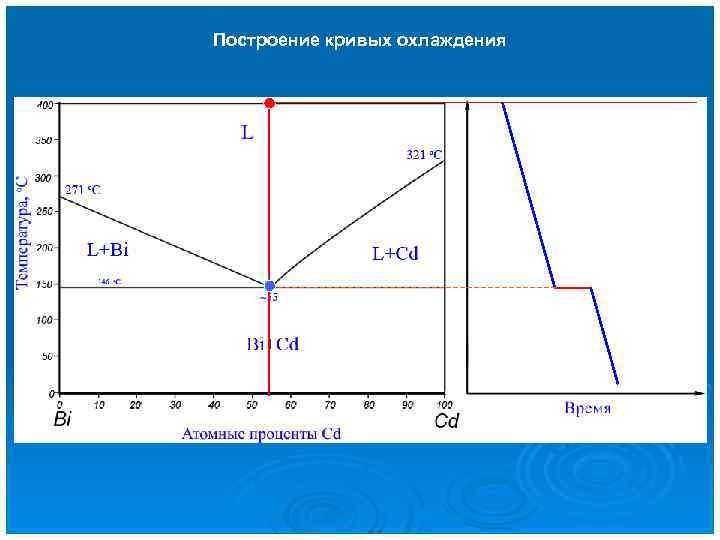
Построение кривых охлаждения
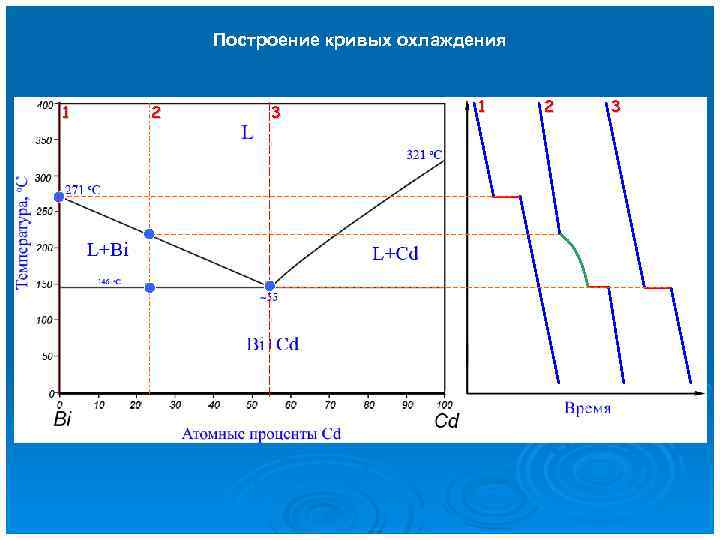
Построение кривых охлаждения 1 2 3
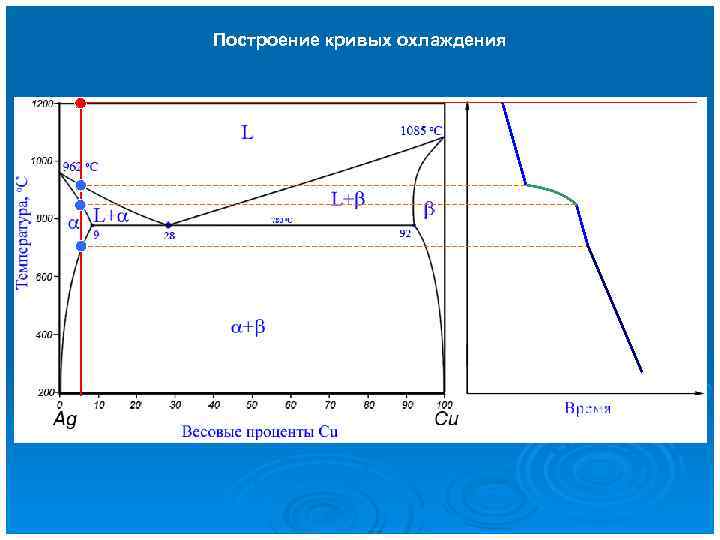
Построение кривых охлаждения
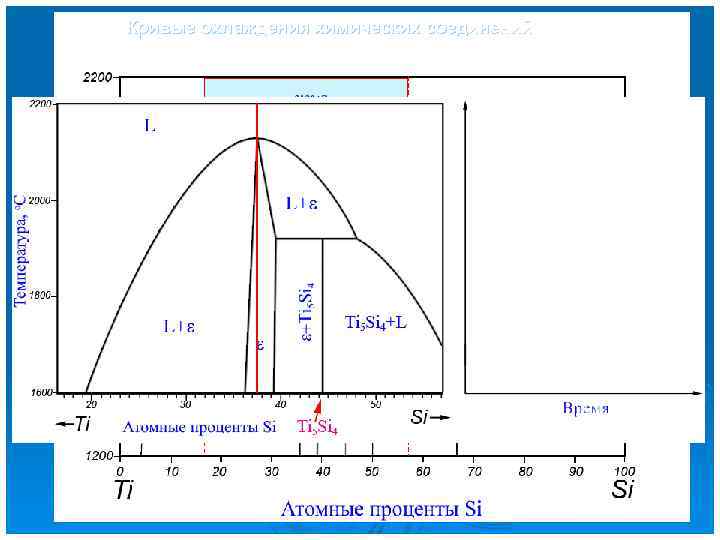
Кривые охлаждения химических соединений (Ti-Si)
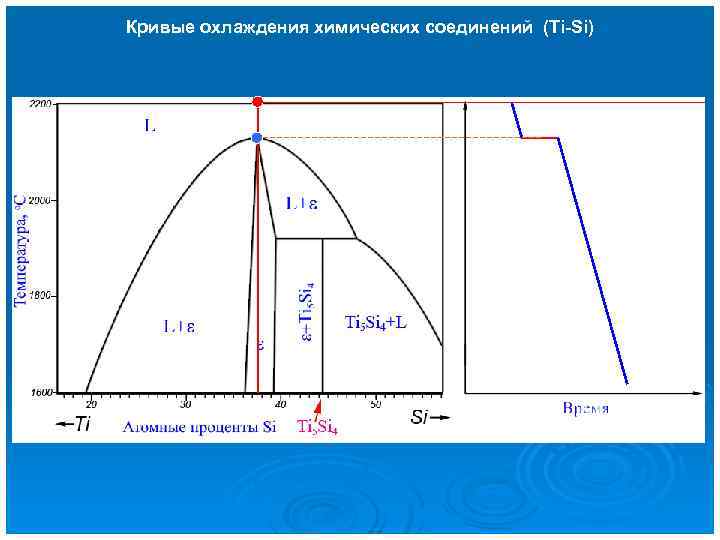
Кривые охлаждения химических соединений (Ti-Si)
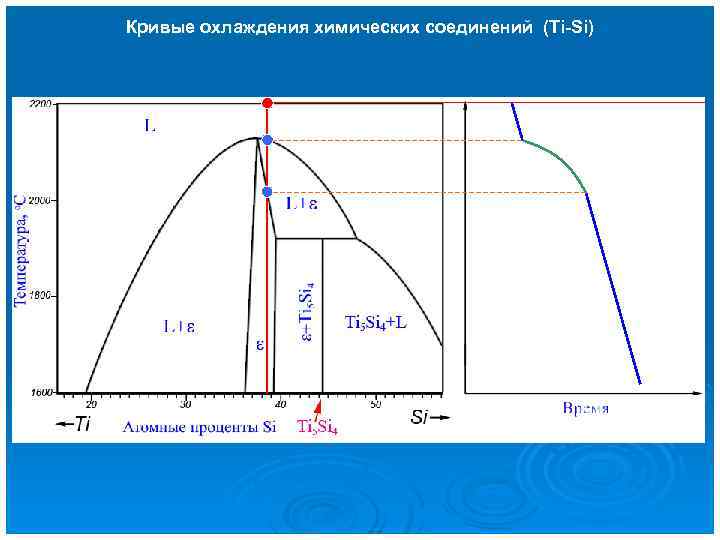
Кривые охлаждения химических соединений (Ti-Si)
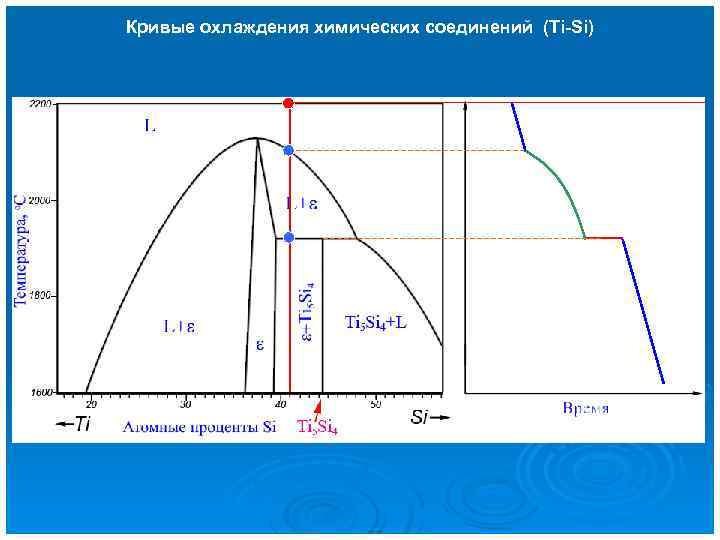
Кривые охлаждения химических соединений (Ti-Si)
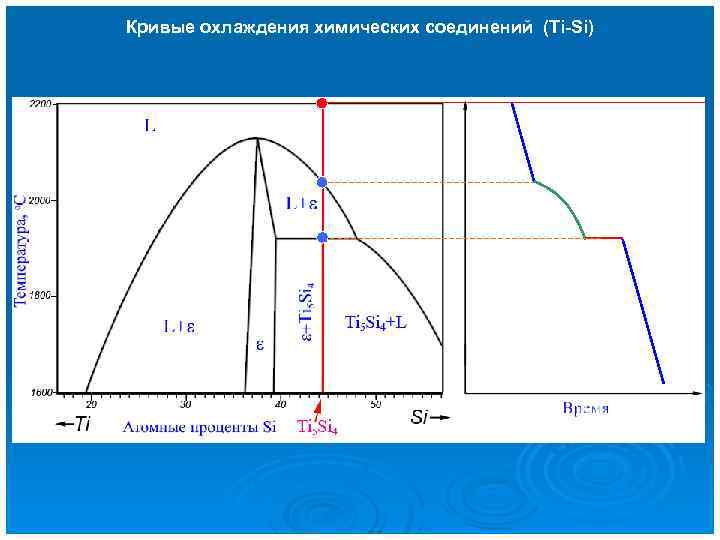
Кривые охлаждения химических соединений (Ti-Si)
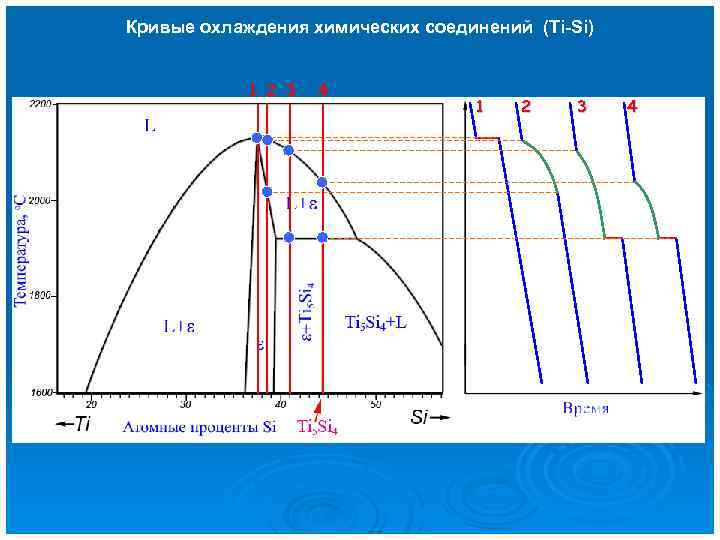
Кривые охлаждения химических соединений (Ti-Si) 1 2 3 4
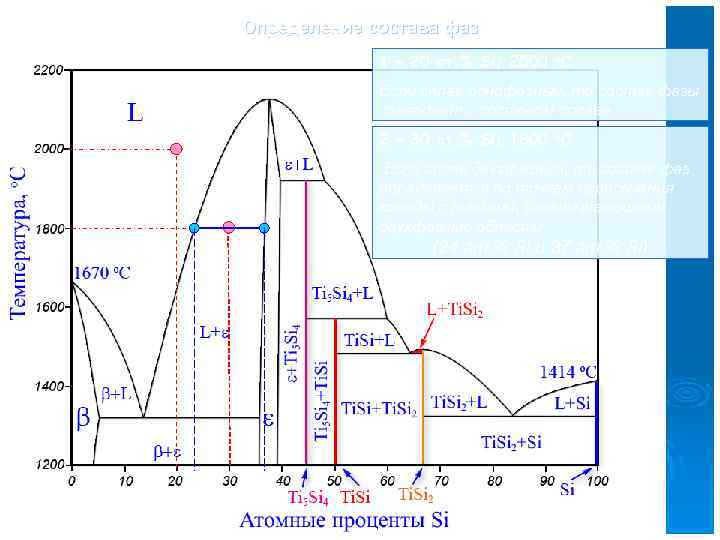
Определение состава фаз 1 – 20 ат. % Si; 2000 o. C Если сплав однофазный, то состав фазы совпадает с составом сплава 1 2 – 30 ат. % Si; 1800 o. C 2 Если сплав двухфазный, то состав фаз определяется по точкам пересечения коноды с линиями, ограничивающими двухфазные области (24 ат. % Si и 37 ат. % Si)
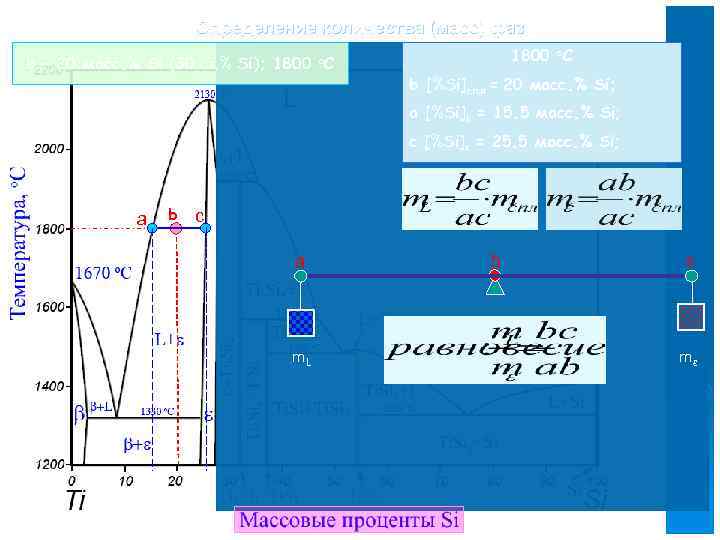
Определение количества (масс) фаз b – 20 масс. % Si (30 ат. % Si); 1800 o. C b [%Si]спл = 20 масс. % Si; a [%Si]L = 15. 5 масс. % Si; c [%Si]ε = 25. 5 масс. % Si; a b c a m. L b c mε
Фазовые Диаграммы.ppt