Faustmann in the Sea Optimal Rotation Time in

Faustmann in the Sea Optimal Rotation Time in Aquaculture By Atle G. Guttormsen Researcher Agricultural University of Norway

Alternative title: To Kill or Not to Kill -Decision Problems in Aquaculture

Outline n n n n Background and Motivation The Problem Previous Studies and Related Problems The Faustmann Solution Problems with the Faustmann Solution and an Extended Faustmann Model Applications on Salmon Summary and Conclusions

Background n n n Aquaculture becomes more and more important Little research done on management issues/decision problems A lot to learn from other industries

Motivation As fish farm enterprise gets larger and the industry more competitive, Optimal production planning and efficient management practice becomes key factors for success.

Decision Problems in Aquaculture § § § When to release juvenile fish How much and when to feed When to harvest § § 1 -2 kg 6 -7 kg etc.

The Feeding Problem n n ”Not” a problem because it’s usually never profitable to feed anything else than either max (to saturation) or nothing. For salmon will feeding 70% of max increase FCR substantially n Means: 70% feeding does not lead to 70% growth.

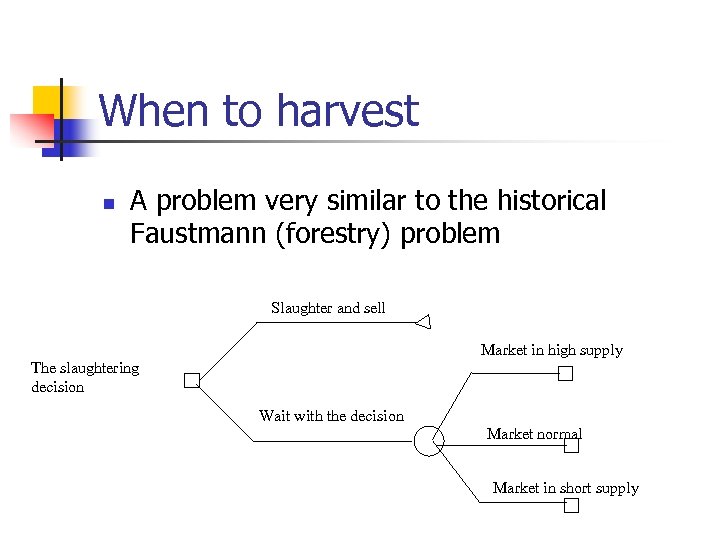When to harvest n A problem very similar to the historical Faustmann (forestry) problem Slaughter and sell Market in high supply The slaughtering decision Wait with the decision Market normal Market in short supply

Related problems n The tree-cutting problem n n From agricultural economics n n Wicksell, Faustmann, Samuelson Cow replacement When to slaughter your pork/broiler When to buy a new tractor Traditional investment problems n Keep the old machine or buy a new one

Previous research on Optimal Harvesting of Farmed “Fish” n n n Bjørndal (1988 and 1990) Arnason (1992) Heaps (1993 and 1994) Hean (1994). Mistiaen & Strand (1998) n n n n Karp, Sadeh and Griffin (1986) Leung & Shang (1989) Leung, Hochman, Wanitprapa, Shang and Wang (1989) Cacho (1990) Hochman, Leung, Rowland, and Wyban (1990) Cacho, Kinnucan and Hatch (1991). Leung, Lee and Hochman (1993)

The Objective n Maximize NPV of the Pen/Pond n n Gives harvesting/rotation time Gives value of the pen/pond

”early” conclusion n n The fish must be harvested when the capital (fish in sea) gives a better return than the opportunity cost. Will always hold, however the problem arise when we want to calculate the opportunity cost.

Without rotation n Bjørndal 1 n Bjørndal 2 (with cost) where l. h. s is marginal revenue, and r. h. s is marginal cost

Faustmann in the sea Continuous Release + Constant p’(w) + Constant p(w) + All rotation periods of equal length Gives in the discrete case S{t}=net fish value V{0}= the capitalized value of the pond/pen immediately prior to releasing new juvenile fish (site value) = The Faustmann Formula

The Problematic Assumptions underlying “Faustmann” § § § Possible to release juvenile fish to seawater continuously during the year One growth function (independent on release time) Constant relationship between prices for different sizes of fish

What makes it difficult ? § Ongoing process § § § Release of juvenile fish only possible during a certain periods of the year Growth is a function of (among other) water temperature § § Rotation Problem Different growth functions for different “starting” times Relationship between prices for different sizes of salmon varies through the year

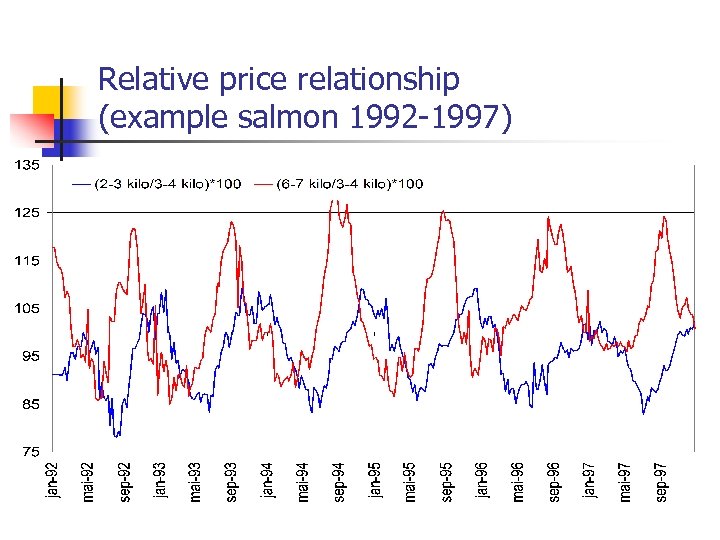Relative price relationship (example salmon 1992 -1997)

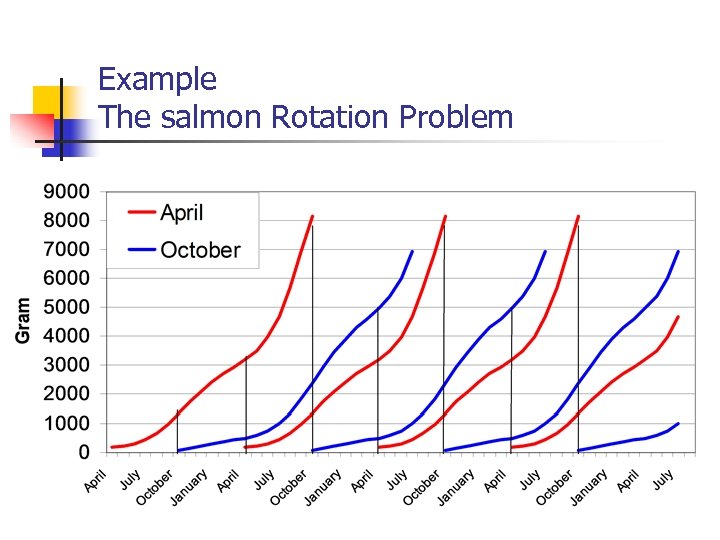Example The salmon Rotation Problem

My Extended Faustmann model n n n Makes the problem discrete Formulate it as a dynamic programming problem Solve it numerically with Matlab

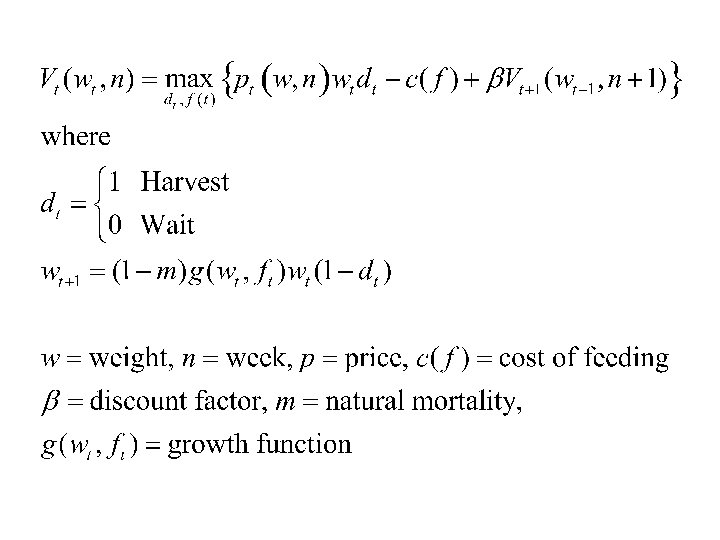
No analytical solutions, must be solved numerically

Examples n n n Tabulated growth functions Constant prices, costs, mortality and interest rates Includes only slaughtering costs (i. e. no release nor feeding cost) Applied on data for Salmon Programmed and Solved in Mat. Lab

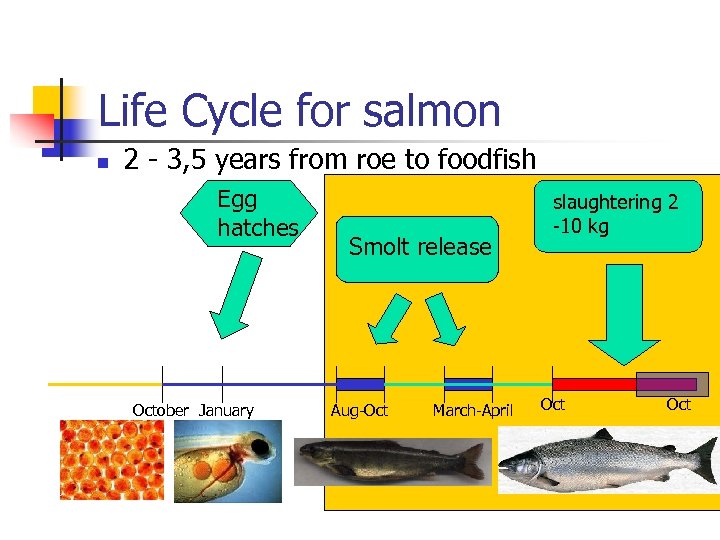Life Cycle for salmon n 2 - 3, 5 years from roe to foodfish Egg hatches October January Smolt release Aug-Oct March-April slaughtering 2 -10 kg Oct

Results the Faustmann model n Typical ”spring”-smolts (150 gram) with ”April” growth function. n n n Slaughter at 19 months Weight 5. 54 kg Typical ”fall”-smolts (50 gram) with ”September” growth function. n n Slaughter at 23 months Weight 5. 65 kg

Results The Extended Model n n Both ”spring” and ”fall” smolts Release possible in n n March, April, May, August, September and October Harvest (month released, weight and kilo) March, 25 months, 6. 2 kg April, 24 months, 6. 0 kg May, 23 months, 5. 7 kg n n n August, 21 months, 4. 7 kg September, 23 months, 5. 3 kg October, 23 months, 5. 6 kg

Further development n n Make more realistic examples Make examples for different species Include more costs Include more constraints n n n Feeding quotas Density regulations Etc.