cc255b2311c0ee3c7103c53756a2a2a7.ppt
- Количество слайдов: 27

Fast Arithmetics © Yohai Devir 2007, Dima Elenbogen 2010, Technion – Israel Institute of Technology
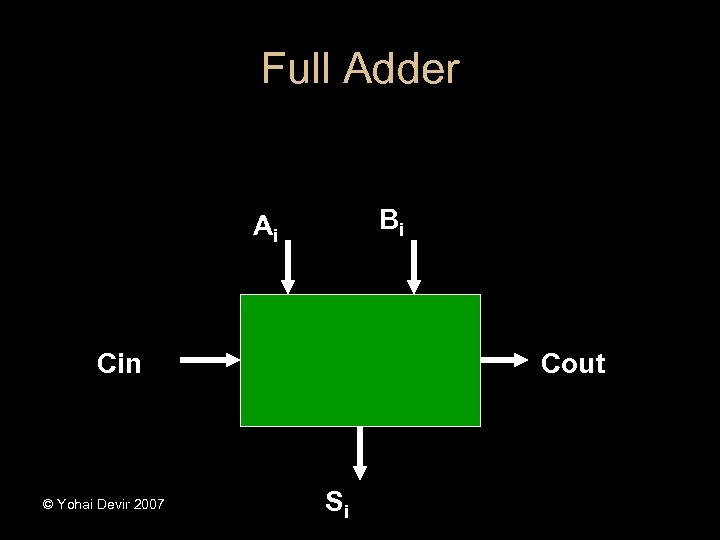
Full Adder Bi Ai Cin © Yohai Devir 2007 Cout Si
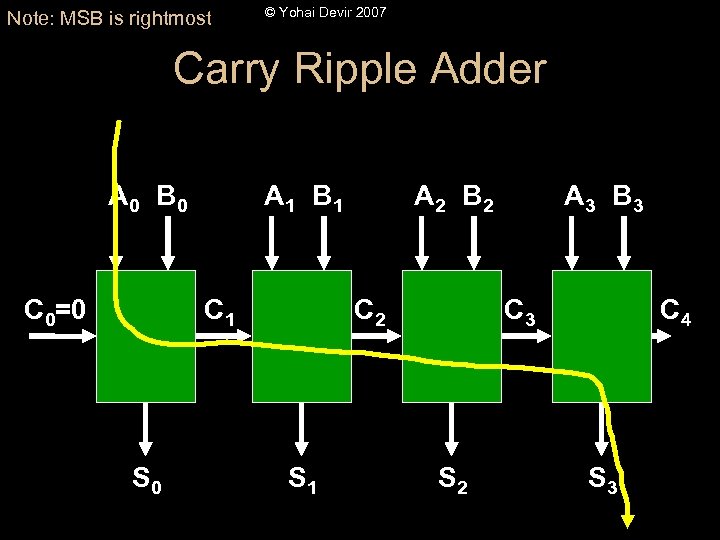
Note: MSB is rightmost © Yohai Devir 2007 Carry Ripple Adder A 0 B 0 C 0=0 A 1 B 1 C 1 S 0 A 2 B 2 C 2 S 1 A 3 B 3 C 3 S 2 C 4 S 3
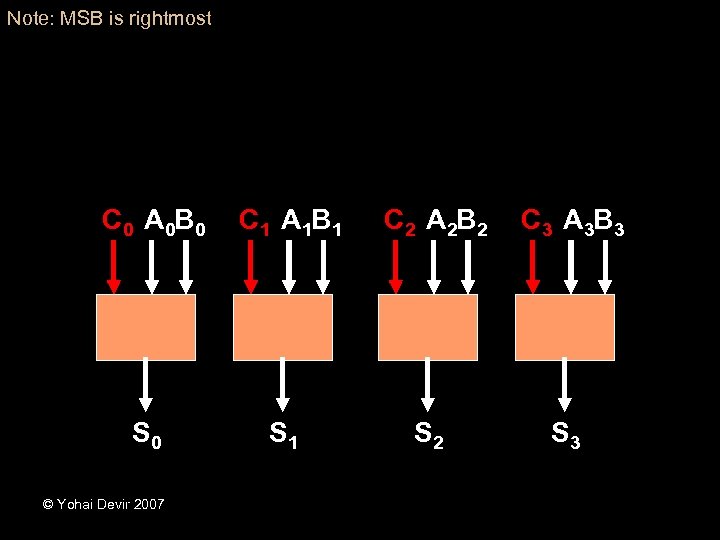
Note: MSB is rightmost C 0 A 0 B 0 C 1 A 1 B 1 C 2 A 2 B 2 C 3 A 3 B 3 S 0 S 1 S 2 S 3 © Yohai Devir 2007

Reduction • Changing the goal to: Calculate the Carry vector • In one time unit we can calculate S out of A, B, C • No effect on complexity © Yohai Devir 2007

© Yohai Devir 2007, Dima Elenbogen 2010, Technion – Israel Institute of Technology Three Cases 1 1 Generate: Gi ? 1 0 Propagate: Pi ? 0 ? 0 Kill Gi Pi
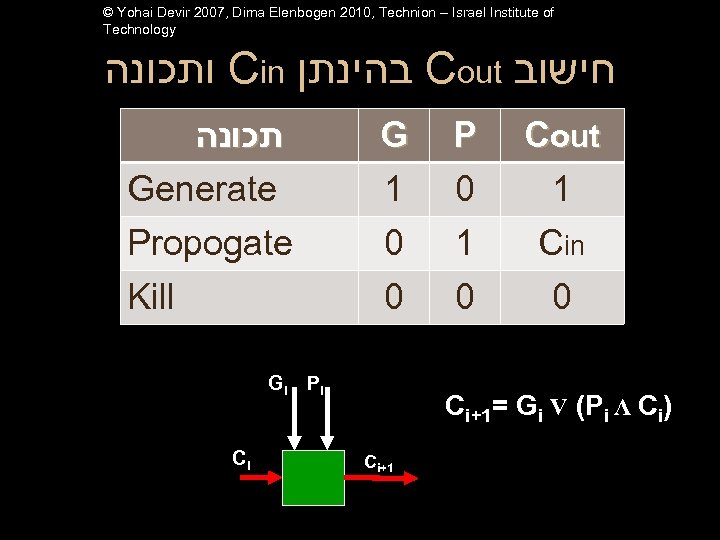
© Yohai Devir 2007, Dima Elenbogen 2010, Technion – Israel Institute of Technology ותכונה Cin בהינתן Cout חישוב תכונה Generate Propogate G 1 0 P 0 1 Cout 1 Cin Kill 0 0 0 Gi Pi Ci Ci+1= Gi V (Pi Λ Ci) Ci+1
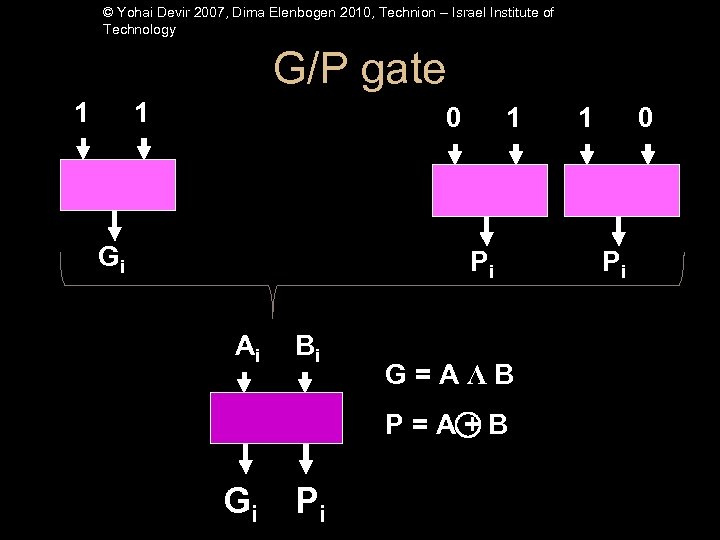
© Yohai Devir 2007, Dima Elenbogen 2010, Technion – Israel Institute of Technology G/P gate 1 1 0 Gi 1 Pi Ai Bi G=AΛB P=A+B Gi Pi 1 0 Pi

Note: MSB is rightmost Calculate using 2 G/P pairs Gi Pi Gi+1 Ci Pi+1 Ci+2 Ci+1 Ci+2=1 Gi+1 V (Gi Λ Pi+1) Ci+2=0 Gi+1=0 Λ Pi+1=0 Ci+2=Ci Pi Λ Pi+1 Gi Pi Gi+1 Pi+1 G’ = Gi+1 V (Gi Λ Pi+1) P’ = Pi Λ Pi+1 G’ P’ © Yohai Devir 2007, Dima Elenbogen 2010, Technion – Israel Institute of Technology
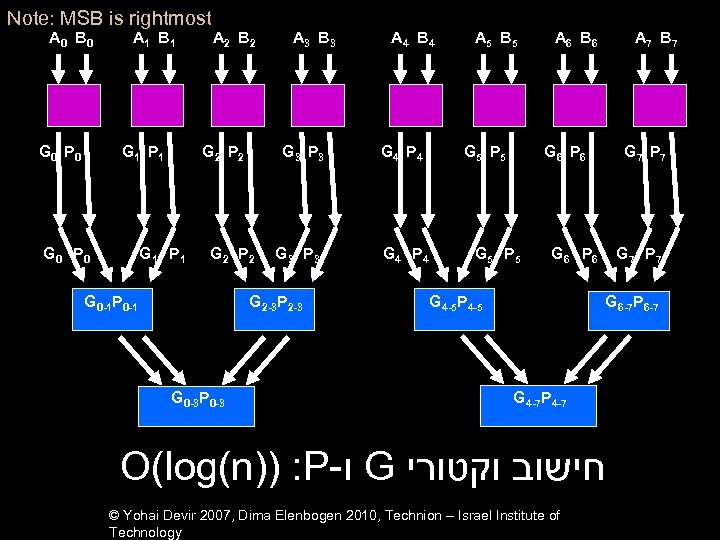
Note: MSB is rightmost A 0 B 0 G 0 P 0 A 1 B 1 G 1 P 1 G 0 P 0 A 2 B 2 G 2 P 2 G 1 P 1 G 3 P 3 G 2 P 2 G 0 -1 P 0 -1 A 3 B 3 G 3 P 3 G 2 -3 P 2 -3 G 0 -3 P 0 -3 A 4 B 4 G 4 P 4 A 5 B 5 G 5 P 5 A 6 B 6 A 7 B 7 G 6 P 6 G 5 P 5 G 7 P 7 G 6 P 6 G 4 -5 P 4 -5 G 7 P 7 G 6 -7 P 6 -7 G 4 -7 P 4 -7 O(log(n)) : P- ו G חישוב וקטורי © Yohai Devir 2007, Dima Elenbogen 2010, Technion – Israel Institute of Technology

חישוב של Gi-j. Pi-j ובלוק Ci בהינתן Cj+1 Note: MSB is rightmost Gi-j Ci Pi-j Cj+1 = Gi-j V (Pi-j Λ Ci) © Yohai Devir 2007, Dima Elenbogen 2010, Technion – Israel Institute of Technology
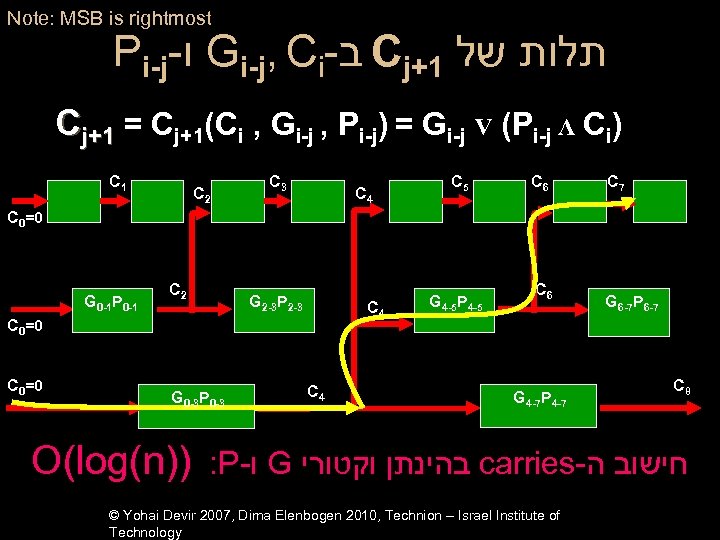
Note: MSB is rightmost Pi-j- ו Gi-j, Ci- ב Cj+1 תלות של Cj+1 = Cj+1(Ci , Gi-j , Pi-j) = Gi-j V (Pi-j Λ Ci) C 1 C 2 C 3 C 4 C 5 C 6 C 7 C 0=0 G 0 -1 P 0 -1 C 2 G 2 -3 P 2 -3 C 4 C 0=0 G 0 -3 P 0 -3 O(log(n)) C 4 G 4 -5 P 4 -5 C 6 G 4 -7 P 4 -7 G 6 -7 P 6 -7 C 8 : P- ו G בהינתן וקטורי carries- חישוב ה © Yohai Devir 2007, Dima Elenbogen 2010, Technion – Israel Institute of Technology
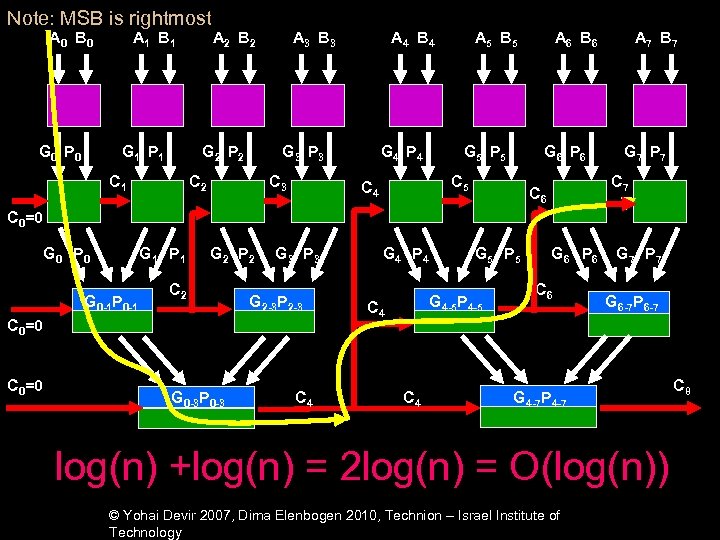
Note: MSB is rightmost A 0 B 0 G 0 P 0 A 1 B 1 G 1 P 1 A 2 B 2 G 2 P 2 C 1 A 3 B 3 A 4 B 4 G 3 P 3 C 2 C 3 G 4 P 4 A 5 B 5 G 5 P 5 G 6 P 6 C 5 C 4 A 6 B 6 A 7 B 7 G 7 P 7 C 6 C 0=0 G 0 P 0 G 1 P 1 G 0 -1 P 0 -1 G 2 P 2 C 2 G 3 P 3 G 2 -3 P 2 -3 C 0=0 G 0 -3 P 0 -3 C 4 G 4 P 4 G 5 P 5 G 4 -5 P 4 -5 C 4 G 6 P 6 C 6 G 7 P 7 G 6 -7 P 6 -7 G 4 -7 P 4 -7 log(n) +log(n) = 2 log(n) = O(log(n)) © Yohai Devir 2007, Dima Elenbogen 2010, Technion – Israel Institute of Technology C 8
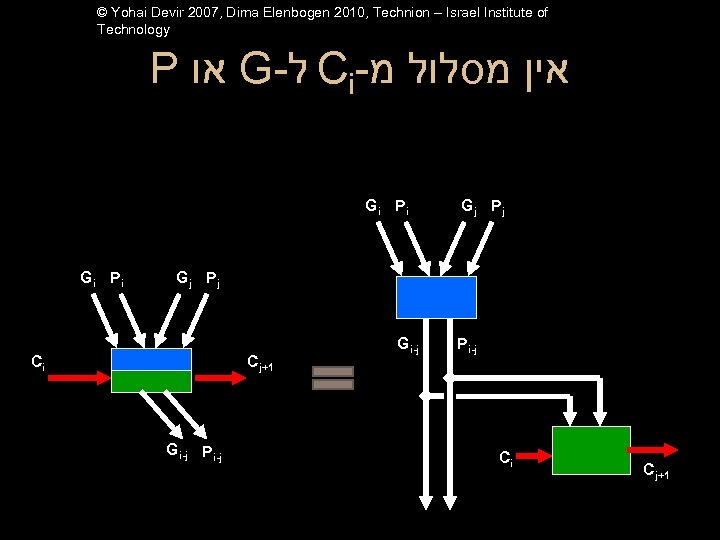
© Yohai Devir 2007, Dima Elenbogen 2010, Technion – Israel Institute of Technology P או G- ל Ci- אין מסלול מ Gi Pi Ci Gj Pj G 0 -1 P 0 -1 Gi-j Pi-j Gj Pj G 0 -1 P 0 -1 Cj+1 Gi-j Pi-j Ci Cj+1

Timeline of Calculations for n=8 C 0 is 0 from the beginning. Ai Bi 1) Gi. Pi for each 0 ≤ i < 8 2) C 1 (by C 0 and G 0 P 0) Gi Pi G 0 -1 P 0 -1, G 2 -3 P 2 -3, G 4 -5 P 4 -5, G 6 -7 P 6 -7 4) C 3 (by C 2 and G 2 P 2) 3) C 2 (by C 0 and G 0 -1 P 0 -1) C 4 (by C 0 and G 0 -3 P 0 -3) G 0 -3 P 0 -3, G 4 -7 P 4 -7 5) C 5 (by C 4 and G 4 P 4) // Now all G. . . P. . . are known C 6 (by C 4 and G 4 -5 P 4 -5) 6) C 7 (by C 6 and G 6 P 6) © Yohai Devir 2007, Dima Elenbogen 2010, Technion – Israel Institute of Technology

Note: MSB is rightmost Final stage C 0 A 0 B 0 C 1 A 1 B 1 C 2 A 2 B 2 Cn-1 An-1 Bn-1 . . . S 0 S 1 S 2 Overall complexity: O(log(n))+1=O(log(n)) © Yohai Devir 2007, Dima Elenbogen 2010, Technion – Israel Institute of Cn Sn-1

Example 2 from. pdf No! Adder Calculation Time Ripple-Carry n Carry-Look-Ahead 2∙log 2 n + 1 CLA is better when: 2∙log 2 n + 1 > n n≥ 6 © Dima Elenbogen 2010, Technion – Israel Institute of Technology

© Yohai Devir 2007, Dima Elenbogen 2010, Technion – Israel Institute of Technology Example 3 from. pdf Gi Ci Pi Gi+1 Ci+1 Pi+1 Gi+2 Ci+2 Pi+2 Ci+3

Note: MSB is rightmost Comparator A==B, A>B Propogate A 0 B 0 A 1 B 1 Generate A 2 B 2 A 3 B 3 EQ 0=1 EQ 2 EQ 3 EQ 4 GR 0=0 GR 1 GR 2 GR 3 GR 4 © Yohai Devir 2007

Note: MSB is rightmost © Yohai Devir 2007 Comparator A==B, A>B A 0 B 0 A 1 B 1 EQ 0 -1 A 0 A 1==B 0 B 1 EQ 0 -1 = EQ 1 Λ EQ 0 GR 1 GR 0 EQ 0 -1 GR 0 -1 A 0 A 1 > B 0 B 1 GR 0 -1 = GR 1 V (GR 0 Λ EQ 1)
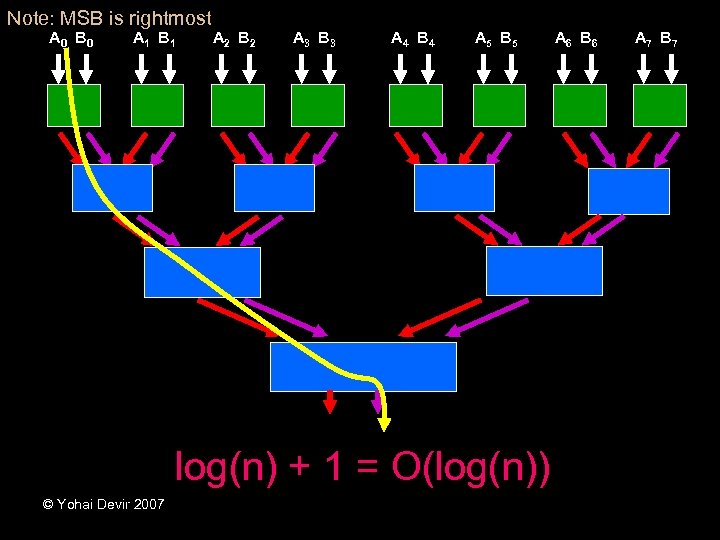
Note: MSB is rightmost A 0 B 0 A 1 B 1 A 2 B 2 A 3 B 3 A 4 B 4 A 5 B 5 log(n) + 1 = O(log(n)) © Yohai Devir 2007 A 6 B 6 A 7 B 7
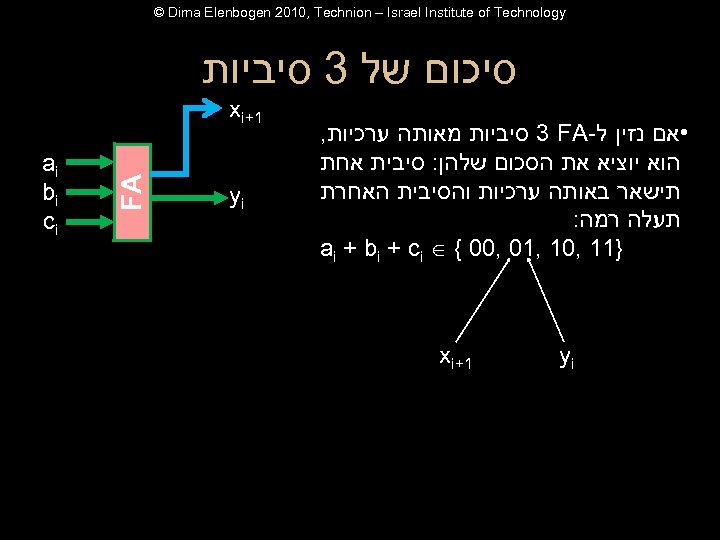
© Dima Elenbogen 2010, Technion – Israel Institute of Technology סיכום של 3 סיביות yi 1+ xi yi FA • אם נזין ל- 3 FA סיביות מאותה ערכיות, הוא יוציא את הסכום שלהן: סיבית אחת תישאר באותה ערכיות והסיבית האחרת תעלה רמה: }11 , 01 , 10 , 00 { ai + bi + ci 1+ xi ai bi ci

© Dima Elenbogen 2010, Technion – Israel Institute of Technology סיכום של 3 מספרים בני j סיביות כ''א FA FA yi ai bi ci 1 - ai 1 - bi 1 - ci FA • אם נזין ל- 3 FA סיביות מאותה ערכיות, הוא יוציא את הסכום שלהן: סיבית אחת תישאר באותה ערכיות והסיבית האחרת תעלה רמה. • טיפול זהה אפשר לבצע במקביל ברמות הערכיות האחרות. • זה מאפשר לנו במעבר יחיד לייצג סכום של 3 מספרים B , A ו- C כזוג מספרים X ו Y כשמתקיים: A + B + C = X + Y • בכל רמה בריחת סיבית אחת למעלה תפוצה ע''י הסיבית המצתרפת מלמטה. • אם אין ממה לפצות )למשל ברמת (LSB אזי משלימים את החסר בעזרת קבוע '0'. • שימו לב ש- X ו- Y הם בני 1+ j סיביות. 1+ xi 2 - ai 2 - bi 2 - ci xi 1 - yi 1 - xi 2 - yi 2 - xi
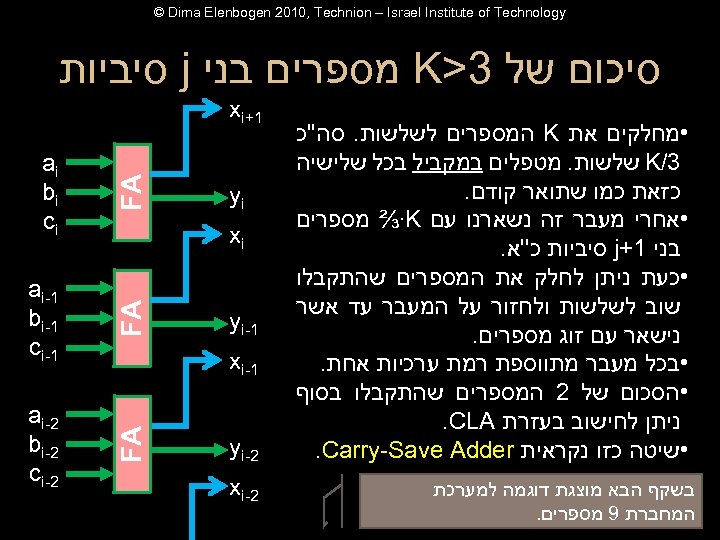
© Dima Elenbogen 2010, Technion – Israel Institute of Technology סיכום של 3> K מספרים בני j סיביות FA FA בשקף הבא מוצגת דוגמה למערכת המחברת 9 מספרים. yi ai bi ci 1 - ai 1 - bi 1 - ci FA • מחלקים את K המספרים לשלשות. סה''כ 3/ K שלשות. מטפלים במקביל בכל שלישיה כזאת כמו שתואר קודם. • אחרי מעבר זה נשארנו עם ⅔∙K מספרים בני 1+ j סיביות כ''א. • כעת ניתן לחלק את המספרים שהתקבלו שוב לשלשות ולחזור על המעבר עד אשר נישאר עם זוג מספרים. • בכל מעבר מתווספת רמת ערכיות אחת. • הסכום של 2 המספרים שהתקבלו בסוף ניתן לחישוב בעזרת . CLA • שיטה כזו נקראית . Carry-Save Adder 1+ xi 2 - ai 2 - bi 2 - ci xi 1 - yi 1 - xi 2 - yi 2 - xi
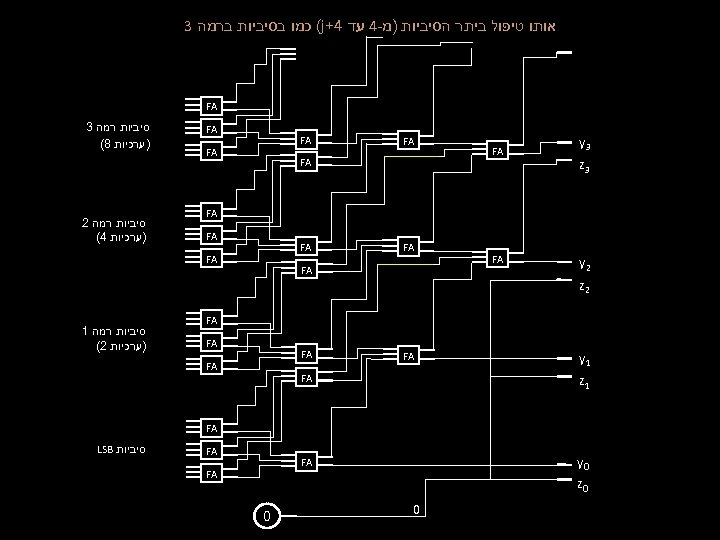
אותו טיפול ביתר הסיביות )מ-4 עד 4+ (j כמו בסיביות ברמה 3 FA 3 y 3 z FA FA 2 y FA FA FA 1 z סיביות רמה 1 )ערכיות 2( FA FA 0 y סיביות רמה 2 )ערכיות 4( FA FA 2 z סיביות רמה 3 )ערכיות 8( FA FA 0 z 0 0 סיביות LSB
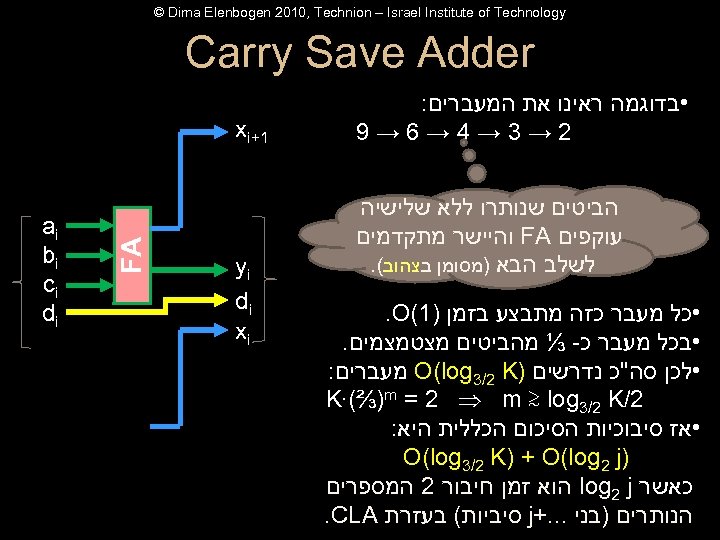
© Dima Elenbogen 2010, Technion – Israel Institute of Technology Carry Save Adder • בדוגמה ראינו את המעברים: 2→ 3→ 4→ 6→ 9 • כל מעבר כזה מתבצע בזמן )1(. O • בכל מעבר כ- ⅓ מהביטים מצטמצמים. • לכן סה''כ נדרשים ) O(log 3/2 K מעברים: 2/ K∙(⅔)m = 2 m ≳ log 3/2 K • אז סיבוכיות הסיכום הכללית היא: ) O(log 3/2 K) + O(log 2 j כאשר log 2 j הוא זמן חיבור 2 המספרים הנותרים )בני. . . + j סיביות( בעזרת . CLA yi di xi FA הביטים שנותרו ללא שלישיה עוקפים FA והיישר מתקדמים לשלב הבא )מסומן בצהוב(. 1+ xi ai bi ci di

! בהצלחה בבחינות ! ואל תעשו בהן טעויות מטופשות © Dima Elenbogen 2010, Technion – Israel Institute of Technology
cc255b2311c0ee3c7103c53756a2a2a7.ppt