Fast and Lock-Free Concurrent Priority Queues for Multi-Thread

Fast and Lock-Free Concurrent Priority Queues for Multi-Thread Systems Håkan Sundell Philippas Tsigas

Outline Synchronization Methods ¢ Priority Queues ¢ Concurrent Priority Queues ¢ l Lock-Free Algorithm: Problems and Solutions Experiments ¢ Conclusions ¢

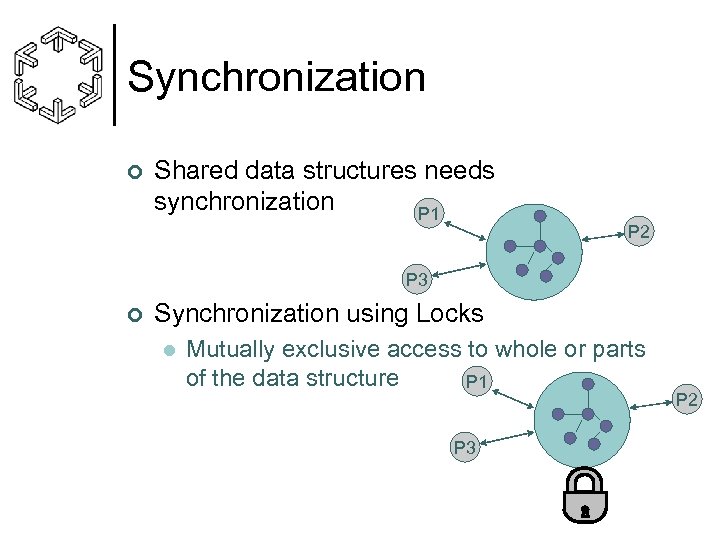Synchronization ¢ Shared data structures needs synchronization P 1 P 2 P 3 ¢ Synchronization using Locks l Mutually exclusive access to whole or parts of the data structure P 1 P 3 P 2

Blocking Synchronization ¢ Drawbacks Blocking l Priority Inversion l Risk of deadlock l ¢ Locks: Semaphores, spinning, disabling interrupts etc. l Reduced efficiency because of reduced parallelism

Non-blocking Synchronization ¢ Lock-Free Synchronization l Optimistic approach • Assumes it’s alone and prepares operation which later takes place (unless interfered) in one atomic step, using hardware atomic primitives • Interference is detected via shared memory and the atomic primitives • Retries until not interfered by other operations • Can cause starvation

Non-blocking Synchronization ¢ Lock-Free Synchronization Avoids problems with locks l Simple algorithms l Fast when having low contention l ¢ Wait-Free Synchronization l Always finishes in a finite number of its own steps. • Complex algorithms • Memory consuming • Less efficient in average than lock-free

Priority Queues Fundamental data structure ¢ Works on a set of pairs ¢ Two basic operations: ¢ l Insert(v, p): Adds a new element to the priority queue l v=Delete. Min(): Removes the element with the highest priority

Sequential Priority Queues ¢ All implementations involves search phase in either Insert or Delete. Min Arrays. Maximum complexity O(N) l Ordered Lists. O(N) l Trees. O(log N) l • Heaps. O(log N) l Advanced structures (i. e. combinations)

Randomized Algorithm: Skip Lists ¢ William Pugh: ”Skip Lists: A Probabilistic Alternative to Balanced Trees”, 1990 l Layers of ordered lists with different densities, achieves a tree-like behavior Head Tail 1 2 l 3 4 5 6 7 Time complexity: O(log 2 N) – probabilistic! … 25% 50%

Why Skip Lists for Concurrent Priority Queues? ¢ Ordered Lists is simpler than Trees l ¢ Search complexity is important l ¢ Skip Lists is an alternative to Trees Lotan and Shavit: “Skiplist-Based Concurrent Priority Queues”, 2000 l L L L Easier to make efficient concurrently L L L 1 Implementation using multiple locks L 2 L L L 3 L 4 L L 5 L 6 L L 7 L

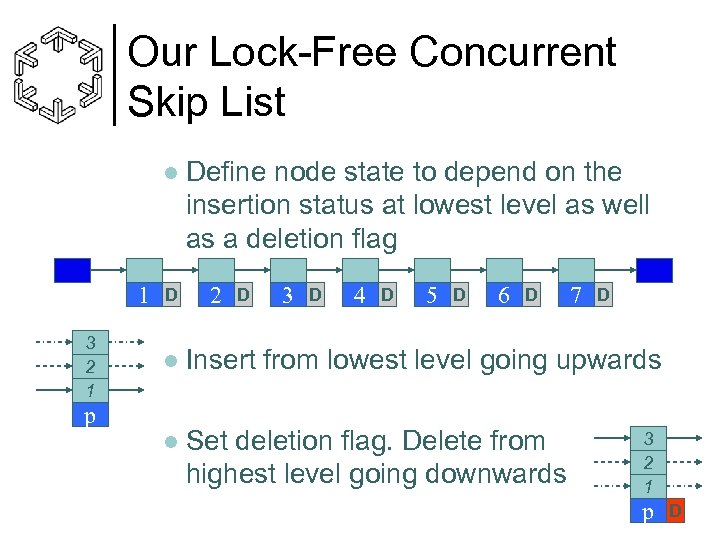Our Lock-Free Concurrent Skip List l 1 3 2 1 D Define node state to depend on the insertion status at lowest level as well as a deletion flag 2 D 3 D 4 D 5 D 6 D 7 D l Insert from lowest level going upwards l Set deletion flag. Delete from highest level going downwards p 3 2 1 p D

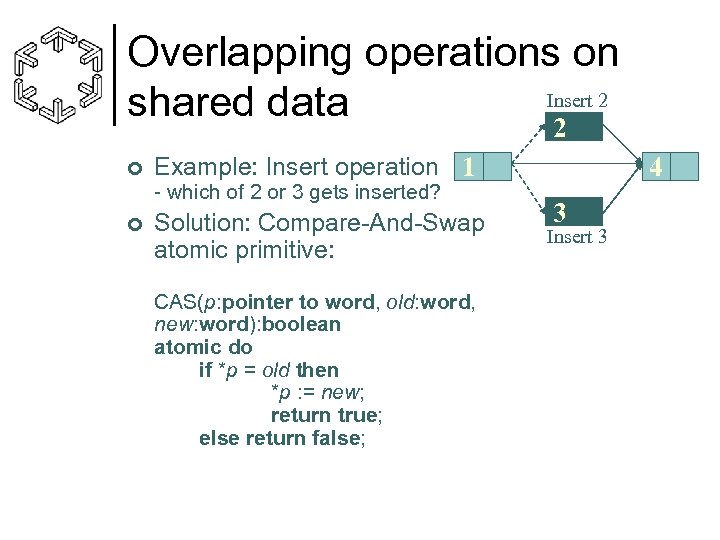Overlapping operations on Insert 2 shared data 2 ¢ Example: Insert operation 1 - which of 2 or 3 gets inserted? ¢ Solution: Compare-And-Swap atomic primitive: CAS(p: pointer to word, old: word, new: word): boolean atomic do if *p = old then *p : = new; return true; else return false; 4 3 Insert 3

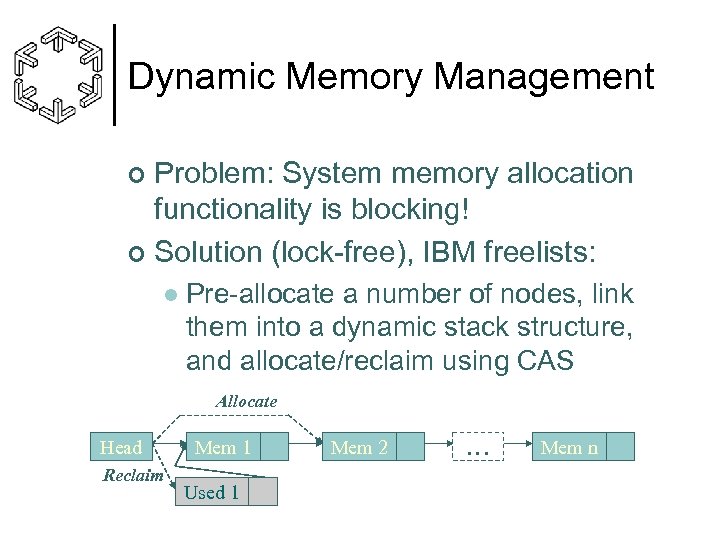Dynamic Memory Management Problem: System memory allocation functionality is blocking! ¢ Solution (lock-free), IBM freelists: ¢ l Pre-allocate a number of nodes, link them into a dynamic stack structure, and allocate/reclaim using CAS Allocate Head Reclaim Mem 1 Used 1 Mem 2 … Mem n

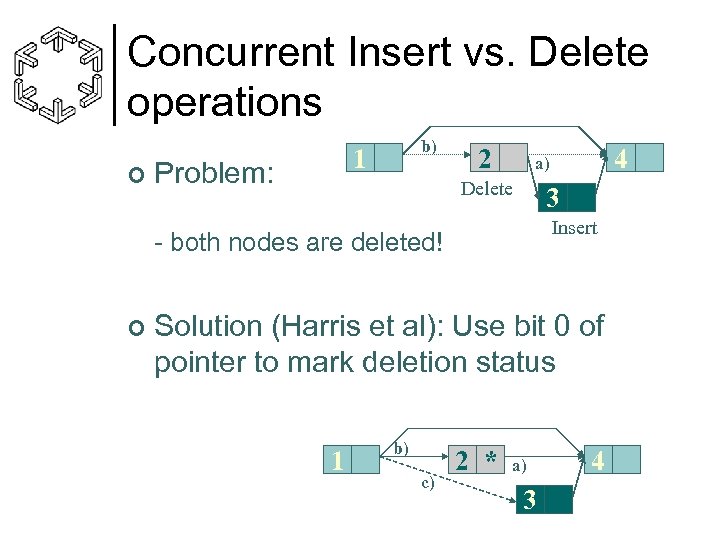Concurrent Insert vs. Delete operations ¢ b) 1 Problem: 2 Delete 3 Insert - both nodes are deleted! ¢ 4 a) Solution (Harris et al): Use bit 0 of pointer to mark deletion status 1 b) c) 2 * a) 3 4

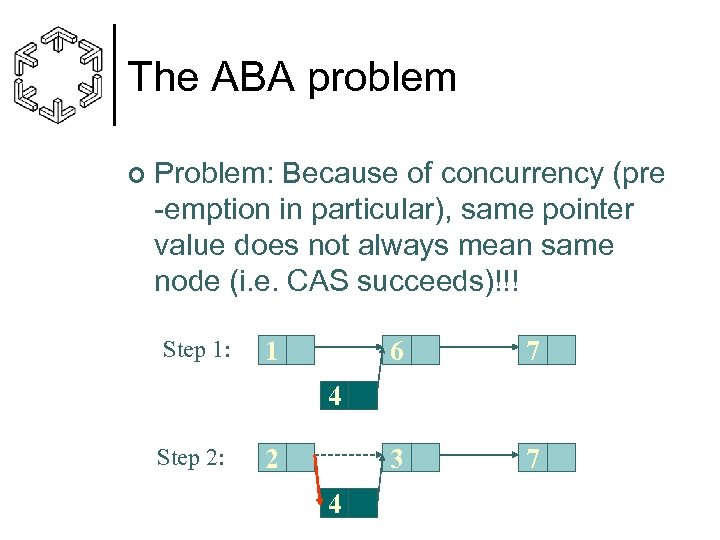The ABA problem ¢ Problem: Because of concurrency (pre -emption in particular), same pointer value does not always mean same node (i. e. CAS succeeds)!!! Step 1: 1 6 7 3 7 4 Step 2: 2 4

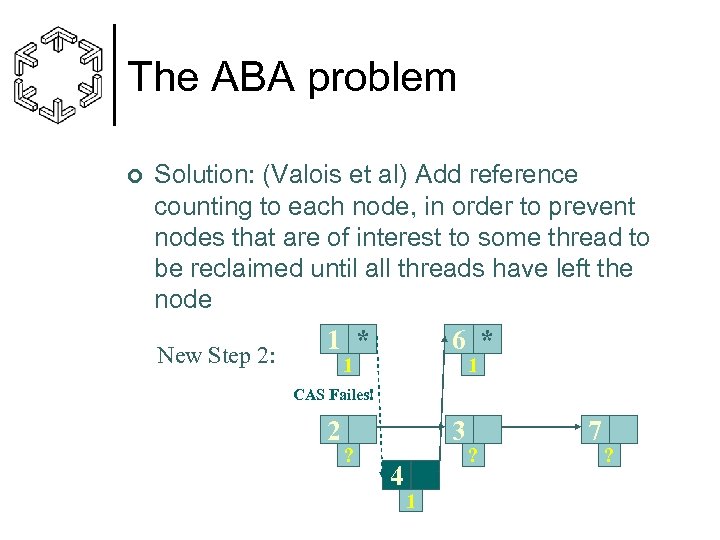The ABA problem ¢ Solution: (Valois et al) Add reference counting to each node, in order to prevent nodes that are of interest to some thread to be reclaimed until all threads have left the node New Step 2: 1 * 6 * 1 1 CAS Failes! 2 ? 3 4 1 ? 7 ?

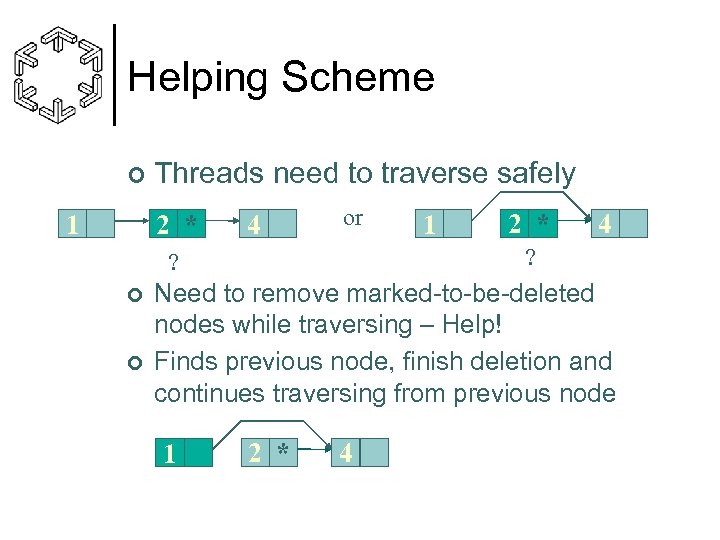Helping Scheme ¢ Threads need to traverse safely 2 * 1 4 or ¢ 2 * 4 ? ? ¢ 1 Need to remove marked-to-be-deleted nodes while traversing – Help! Finds previous node, finish deletion and continues traversing from previous node 1 2 * 4

Back-Off Strategy ¢ ¢ ¢ For pre-emptive systems, helping is necessary for efficiency and lock-freeness For really concurrent systems, overlapping CAS operations (caused by helping and others) on the same node can cause heavy contention Solution: For every failed CAS attempt, back-off (i. e. sleep) for a certain duration, which increases exponentially

Our Lock-Free Algorithm ¢ Based on Skip Lists l ¢ ¢ Uses CAS atomic primitive Lock-Free memory management l l ¢ ¢ ¢ Treated as layers of ordered lists IBM Freelists Reference counting Helping scheme Back-Off strategy All together proved to be linearizable

Experiments 1 -30 threads on platforms with different levels of real concurrency ¢ 10000 Insert vs. Delete. Min operations by each thread. 100 vs. 1000 initial inserts ¢ Compare with other implementations: ¢ Lotan and Shavit, 2000 l Hunt et al “An Efficient Algorithm for Concurrent Priority Queue Heaps”, 1996 l

Full Concurrency

Medium Pre-emption

High Pre-emption

Conclusions ¢ ¢ Our work includes a Real-Time extension of the algorithm, using time-stamps and a time -stamp recycling scheme Our lock-free algorithm is suitable for both pre-emptive as well as systems with full concurrency l ¢ Will be available as part of NOBLE software library, http: //www. noble-library. org See Technical Report for full details, http: //www. cs. chalmers. se/~phs

Questions? ¢ Contact Information: l l l Address: Håkan Sundell vs. Philippas Tsigas Computing Science Chalmers University of Technology Email: @ cs. chalmers. se Web: http: //www. cs. chalmers. se/~phs/warp

Semaphores

Back-off spinlocks

Jones Skew-Heap

The algorithm in more detail ¢ Insert: 1. 2. 3. 4. 5. ¢ Create node with random height Search position (Remember drops) Insert or update on level 1 Insert on level 2 to top (unless already deleted) If deleted then Help. Delete(1) All of this while keeping track of references, help deleted nodes etc.

The algorithm in more detail ¢ Delete. Min 1. 2. 3. 4. ¢ Mark first node at level 1 as deleted, otherwise Help. Delete(1) and retry Mark next pointers on level 1 to top Delete on level top to 1 while detecting helping, indicate success Free node All of this while keeping track of references, help deleted nodes etc.

The algorithm in more detail ¢ Help. Delete(level) 1. 2. 3. 4. ¢ Mark next pointer at level to top Find previous node (info in node) Delete on level unless already helped, indicate success Return previous node All of this while keeping track of references, help deleted nodes etc.

Correctness ¢ Linearizability (Herlihy 1991) l In order for an implementation to be linearizable, for every concurrent execution, there should exist an equal sequential execution that respects the partial order of the operations in the concurrent execution

Correctness ¢ ¢ Define precise sequential semantics Define abstract state and its interpretation l ¢ Define linearizability points l ¢ Show that state is atomically updated Show that operations take effect atomically at these points with respect to sequential semantics Creates a total order using the linearizability points that respects the partial order l The algorithm is linearizable

Correctness ¢ Lock-freeness l ¢ At least one operation should always make progress There are no cyclic loop depencies, and all potentially unbounded loops are ”gate-keeped” by CAS operations l The CAS operation guarantees that at least one CAS will always succeed • The algorithm is lock-free

Real-Time extension ¢ Delete. Min operations should ignore nodes that are inserted after the Delete. Min operation started Nodes are inserted together with a timestamp l Because timestamps are only used for relative comparisons, no need for a real-time clock l • Generate time-stamps by increasing function

Real-Time extension ¢ Timestamps are potentially unbounded and will overflow l ¢ Recycle ”wrapped-over” timestamp values by having Tag. Field. Size=Max. Tag*2 Timestamps at nodes can stay forever (Max. Tag => unlimited) l Every operation traverses one step through the Skiplist and updates ”too old” timestamps