Fast algorithm for detecting community structure in networks

Fast algorithm for detecting community structure in networks. . (M. E. J. Newman, (2004 Presented by Muad Abu-Ata

Community structure • groups of vertices within which connections are dense but between which they are sparser. • Within-group( intra-group) edges. – High density • Between-group( inter-group) edges. – Low density.

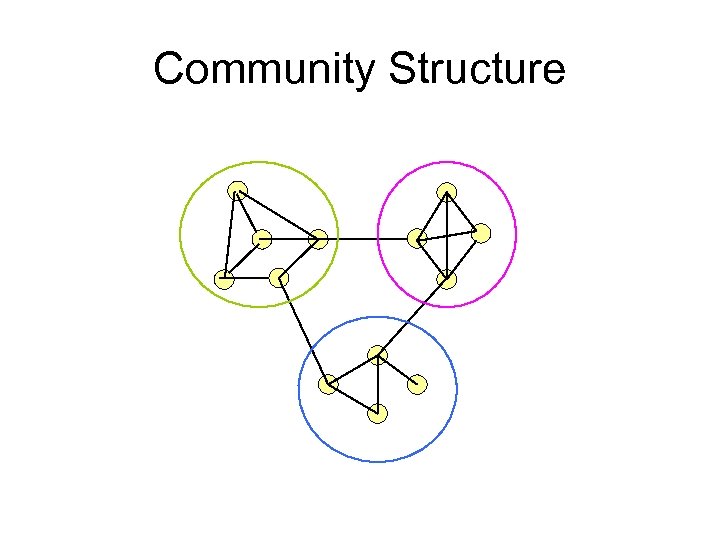Community Structure

Real Word Networks • • Internet World Wide Web. Citation Networks. Transportation Network. Email Networks. Food Webs. Social Networks. Biochemical Networks.

Examples of Community Structures • Communities of biochemical network correspond to functional units of some kind. • Communities of a web graph correspond to sets of web sites dealing with a related topics.

Finding Community Structures • Divide the network into non-empty groups( communities) in such a way that every vertex belongs to one of the communities. • Many possible divisions could be done. • We need a good division. • Measurement of good division.

Community Detection Approaches • Graph partitioning approaches: – Spectral bisection – The Kernighan-Lin (KL) algorithm • Hierarchical clustering. • The algorithm of Girvan and Newman. • The Newman fast algorithm.

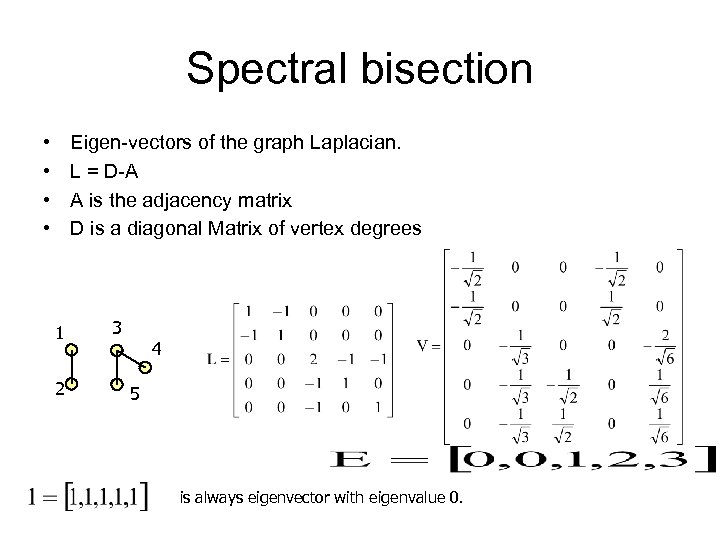Spectral bisection • • Eigen-vectors of the graph Laplacian. L = D-A A is the adjacency matrix D is a diagonal Matrix of vertex degrees 1 2 3 4 5 is always eigenvector with eigenvalue 0.

Bisect ! 1 2 3 4 5 The eigenvector corresponding to the lowest eigenvalue must have both positive and negative elements. +ve: reasonably fast; O(n 3) sparse matrix case, Lancozos method reduces it to approximately to

(. Spectral Bisection (Cont • Disadvantages: • It only bisects graphs into 2 communities. Division into a larger number of communities is usually achieved by repeated bisection, but this does not always give satisfactory results. • we do not in general know ahead of time how many communities we want to divide the graph into.

The Kernighan-Lin( KL) algorithm • 1. 2. 3. 4. Benefit function Q: the number of edges that lie within the two groups minus the number that lie between them. user specify the size of the two groups A & B. divide the vertices into the two groups randomly. Calculate the ∆Q for all possible exchange pair from A and B. Swap the pair that maximizes the change of Q. (greedy algorithm) 5. Repeat 3 & 4 until all vertices have been swapped once. (any vertex that has been swapped is never swapped. ) 6. Go back over the sequence of swaps and find the highest Q.

(. KL algorithm (cont Time complexity: O(n 2). -ve: requires a priori what the size of the groups will be. Running the algorithm for all possible group sizes O(n 3). The best values of Q are always achieved for very asymmetric trivial division.

Hierarchical clustering • develop a similarity (or dissimilarity) measure xij between pairs (i, j) of vertices. • Apply the hierarchical clustering and build the dendogram or tree. • Cross section the dendogram at any level will give the communities at that level.

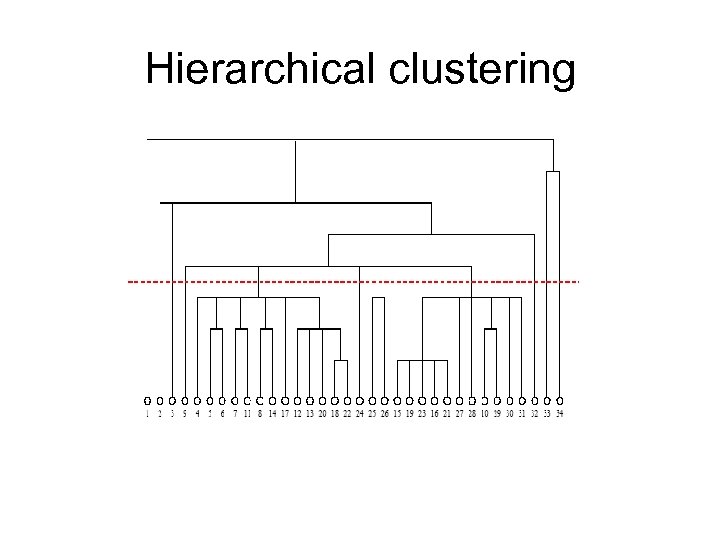Hierarchical clustering

Hierarchical clustering • Time complexity: O(n 2 logn) • N 2 vertex pairs. • Calculations of all similarity measures take O (mn). • Sorting N 2 similarity measures takes O(n 2 logn) for sorting. • Constructing the dendogram takes linear time. • it doesn't require us to specify the size or number of groups we want to look for beforehand. • -ve: – It does not tell us how many groups should be used to get the best division of the network (Where to cut!).

Girvan and Newman( GN) Algorithm 1. Edge Betweeness: The number of shortest paths between vertex pairs that goes along an edge. A B 2. 3. 4. Calculate the betweenness for all edges in the network. Remove the edge with the highest betweenness. Recalculate betweennesses for all edges affected by the removal. Repeat from step 2 until no edges remain. 5. 6. • cross cut the dendogram of components. By removing these edges, we separate groups from one another as components.

The GN Algorithm

The GN Algorithm • Time complexity: – O(m 2 n) O(n 3) • O( mn) for calculating edge betweeness. • m iterations. • -ve: – It provides no guide to how many communities a network should be split into (where to cross cut!). modularity measure.

Newman Fast Algorithm • Modularity Measure • the fraction of within-community edges minus the expected value of the same quantity for randomized network( edges fall at random with no regard to community structure) • Q= 0 no community structure. • 0. 3

Newman Fast Algorithm 1. 2. 3. 4. 5. Separate each vertex solely into n community. Calculate ∆Q for all possible community pairs. Merge the pair of the largest increase in Q. Repeat 2 & 3 until all communities merged in one community. Cross cut the dendogram where Q is maximum Notes: ∆Q=eij+ eji – 2 aiaj Calculate ∆Q only for pairs that are connected by an edge.

Newman Fast Algorithm

Newman Fast Algorithm

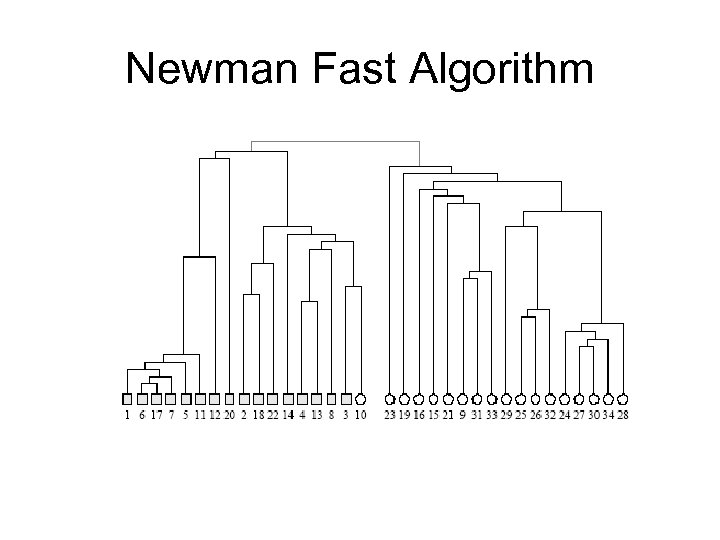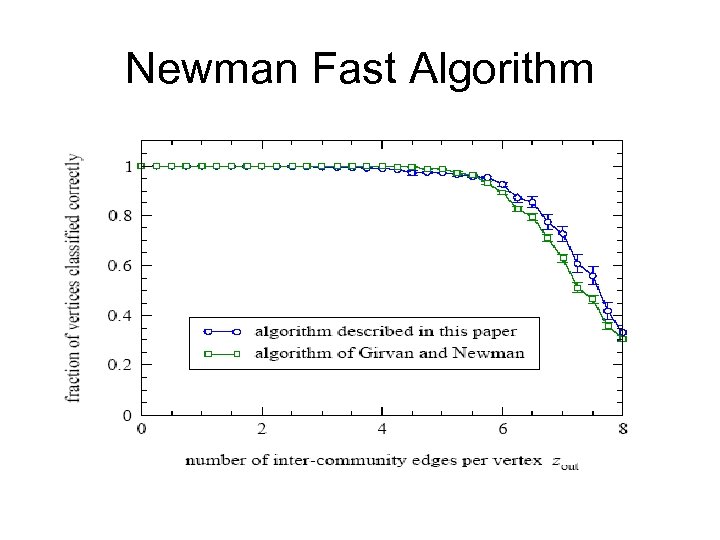Newman Fast Algorithm • Time Complexity – O((m+n)n) O(n 2) for sparse graphs

Conclusion • Newman fast algorithm is: – considerably fast O(n 2) – gives good divisions. – No need a prior knowledge of the community sizes. – No need a prior knowledge of the number of communities.

References • Fast algorithm for detecting community structure in networks, M. E. J. Newman. • Detecting community structure in network, M. E. J. Newman. • Finding community structure in very large networks, Aaron Clauset, M. E. J. Newman, and Cristopher Moore.