Fall 2009 The Chinese University of Hong Kong

Fall 2009 The Chinese University of Hong Kong CSC 3130: Automata theory and formal languages Turing Machines Andrej Bogdanov http: //www. cse. cuhk. edu. hk/~andrejb/csc 3130

What is a computer? input data instructions (program) computer output data A computer is a machine that manipulates data according to a list of instructions.

Are DFAs and PDAs computers? 0 1 0, e / a 1, a / e #, e / e e, Z 0 / e 0, 1 yes no! A computer is a machine that manipulates data according to a list of instructions.

A short history of computing devices slide rule (1600 s) abacus (Babylon 500 BC, China 1300) Leibniz calculator (1670 s) Babbage’s mechanical engine (1820 s)

A brief history of computing devices Z 3 (Germany, 1941) ENIAC (Pennsylvania, 1945) PC (1980) Mac. Book Air (2008)

Which of these are “real” computers? not programmable

Computation is universal In principle, all these computers have the same problem-solving ability C++ java python LISP

The Turing Machine C++ java python LISP

The Turing Machine • The Turing Machine is an abstract automaton that is meant to model any physically realizable computer – Using any technology (mechanical, electrical, nano, bio) – Under any physical laws (gravity, quantum, E&M) – At any scale (human, quantum, cosmological) • How come there is one model that can capture all these vastly different settings? • Why do we need an abstract model of a computer?

Computation and mathematical proofs • Prove that. . . √ 2 is irrational. (Archimedes’ Theorem) G = (L, R) has a perfect matching iff | (S)| ≥ |S| for every L ⊆ S. (Hall’s Theorem) The equation The language 0 n 1 n is not regular. n + y n = z n, n ≥ 2 x has no integer solutions. (Fermat-Wiles Theorem) Math is hard, let’s go shopping!

Hilbert’s list of 23 problems • Leading mathematician in the 1900 s • At the 1900 International Congress of Mathematicians, proposed a list of 23 problems for the 20 th century David Hilbert (1862 -1943) • Hilbert’s 10 th problem: Find a method for telling if an equation like xyz – 3 xy + 6 xz + 2 = 0 has integer solutions

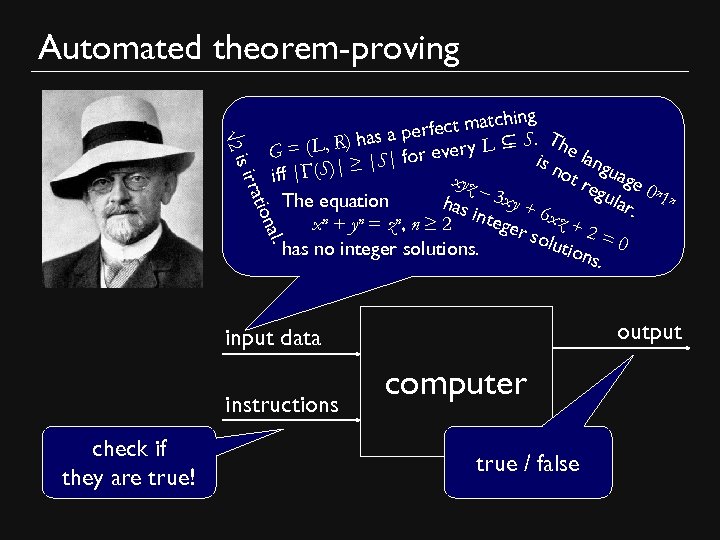Automated theorem-proving √ 2 l. ona rati is ir hing fect matc a per. T L, R) has =( ry L ⊆ S i he la G eve n sn ≥ |S| for ot guag | (S)| iff xyz reg e 0 n – 3 x ula n The equation y+ has r. 1 6 i xn + yn = zn, n ≥ 2 nteger xz + 2 solu = tion 0 has no integer solutions. s. output input data instructions check if they are true! computer true / false

Automated theorem proving • How could automated theorem proving work? • Let’s look at a typical proof: Theorem: √ 2 is irrational. Proof: Assume not. Then √ 2 = m/n. Then m 2 = 2 n 2 But m 2 has an even number of prime factors and 2 n 2 has an odd number of prime factors. Contradiction.

First idea of automated theorem proving ➀ • Checking that a proof is correct is much easier than coming up with the proof Proof: √ 2 = m/n (√ 2)n = m both sides ×n square Assume not. Then √ 2 = m/n. (√ 2)2 n 2 = m 2 def of sqrt 2 = 2 n 2 Then m 2 2 But m 2 has an even. . . 2 n = m and 2 n 2 has an odd. . . Contradiction. . if we write out the proof in sufficient detail

First idea of automated theorem proving ➀ • Checking that a proof is correct is much easier than coming up with the proof A proof, if written out in sufficient detail, can be checked mechanically – In principle this is uncontroversial – In practice, it is harder (but still possible) to do

Second idea of automated theorem proving ➁ • To find if statement is true, why don’t we try all possible proofs After all, a proof is just a sequence of symbols (over alphabet {0, 1, 2, m, n, √, 2, etc. }) If statement is true, it has a proof of finite length, say k To find it, let’s just try all possible proofs of length 1, 2, up to k √ 2 = m/n (√ 2)n = m (√ 2)2 n 2 = m 2. . .

Königsberg, 1930 David Hilbert Kurt Gödel (1862 -1943) (1906 -1978) September 8: Hilbert gives a famous lecture “Logic and the understanding of nature”

Königsberg, 1930 It is all over! David Hilbert Kurt Gödel (1862 -1943) (1906 -1978) John von Neumann (1903 -1957) I reached the conclusion that in any reasonable formal system in which provability in it can be expressed as a property of certain sentences, there must be propositions which are undecidable in it.

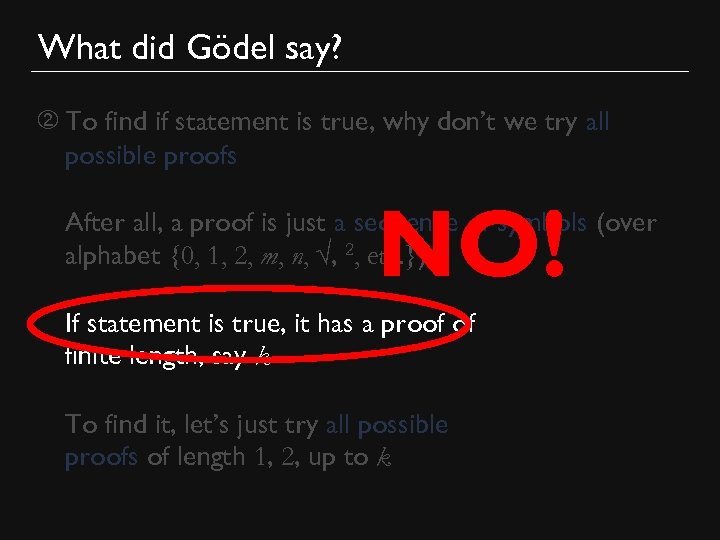What did Gödel say? ➁ • To find if statement is true, why don’t we try all possible proofs NO! After all, a proof is just a sequence of symbols (over alphabet {0, 1, 2, m, n, √, 2, etc. }) If statement is true, it has a proof of finite length, say k To find it, let’s just try all possible proofs of length 1, 2, up to k

Gödel’s incompleteness theorem Some mathematical statements are true but not provable. What are they?

Example of incompleteness • Recall Hilbert’s 10 th problem: Find a method for telling if an equation like xyz – 3 xy + 6 xz + 2 = 0 has integer solutions • Matyashievich showed in 1970 that there exists a polynomial p such that p(x 1, . . . , xk) = 0 has no integer solutions, but this cannot be proved

Another example of incompleteness • Recall ambiguous context free grammars • We did exercises of the type “Show that G is ambiguous” • However there exists a CFG G such that G is unambiguous, but this cannot be proved

www. logicomix. com

Gödel’s incompleteness theorem Some mathematical statements are true but not provable. What does this have to do with computer science?

The father of modern computer science • Invented the Turing Test to tell humans and computers apart • Broke German encryption codes during World War II Alan Turing • The Turing Award is the “Nobel prize of Computer Science” (1912 -1954) 1936: “On Computable Numbers, with an Application to the Entscheidungsproblem”

Turing’s angle on incompleteness mathematical statement input data instructions computer check if true! output true / false Gödel’s theorem says that a computer cannot determine the truth of mathematical statements But there are many other things!

Computer program analysis public static void main(String args[]) { System. out. println("Hello World!"); } What does this program do? public static void main(String args[]) { int i = 0; for (j = 1; j < 10; j++) { i += j; if (i == 28) { System. out. println("Hello World!"); } } } How about this one?

Computers cannot analyze programs! java program input data instructions does it print Hello, world! computer output The essence of Gödel’s theorem is that computers cannot analyze computer programs

How do you argue things like that? To argue what computers cannot do, we need to have a precise definition of what a computer is. 1936: “On Computable Numbers, with an Application to the Entscheidungsproblem” Section 1. Computing Machines

Turing Machines • A Turing Machine is a finite automaton with a two-way access to an infinite tape state control input 0 1 0 … infinite tape • Initially, the first few cells contain the input, and the other cells are blank

Turing Machines • At each point in the computation, the machine sees its current state and the symbol at the head state control 0 1 a 0 … • It can replace the symbol on the tape, change state, and move the head left or right

How Turing Machines operate current state q 1 a/b. L q 2 0 1 a 0 … Replace a with b, and move head left current state q 1 a/b. L q 2 0 1 b 0 …

Formal Definition A Turing Machine is (Q, , q 0, qacc, qrej): – – – Q is a finite set of states; is the input alphabet; is the tape alphabet ( ) including the blank symbol ☐ q 0 in Q is the initial state; qacc, qrej in Q are the accepting and rejecting state; is the transition function : (Q – {qacc, qrej}) →Q {L, R}

Operation of Turing Machines q 0 0 0 1 ☐ ☐ … Initially, tape contains input followed by blanks • Differences from pushdown automata – TM can access arbitrary entries in memory – Transitions in TM are deterministic – TM uses same tape for input and memory

Programming Turing Machines L 1 = {w$w: w ∈{a, b}*} Strategy: Read and remember the first symbol abbaa$abbaa Cross it off (x) xbbaa$abbaa Read the first symbol past $ xbbaa$abbaa If they don’t match, reject If they do, cross it off xbbaa$xbbaa

Programming Turing Machines L 1 = {w$w: w ∈{a, b}*} Strategy: Look for the first uncrossed symbol xbbaa$xbbaa Cross it off (x) xxbaa$xbbaa Read the first uncrossed symbol past $ xxbaa$xbbaa If they match, cross it off, else reject xxbaa$xxbaa At the end, there should be only xs and $s xxxxx$xxxxx If not, reject

Programming Turing Machines Description of Turing Machine: L 1 = {w$w: w ∈{a, b}*} 1 Until you reach $ 7 Read and remember entry Write x Move right past $ and past all xs If this entry is different, reject Otherwise Write x Move left past $ and to right of first x 8 If you see only xs followed by ☐, accept 2 3 4 5 6 xbbaa$xbbaa xxbaa$xbbaa xxbaa$xxbaa

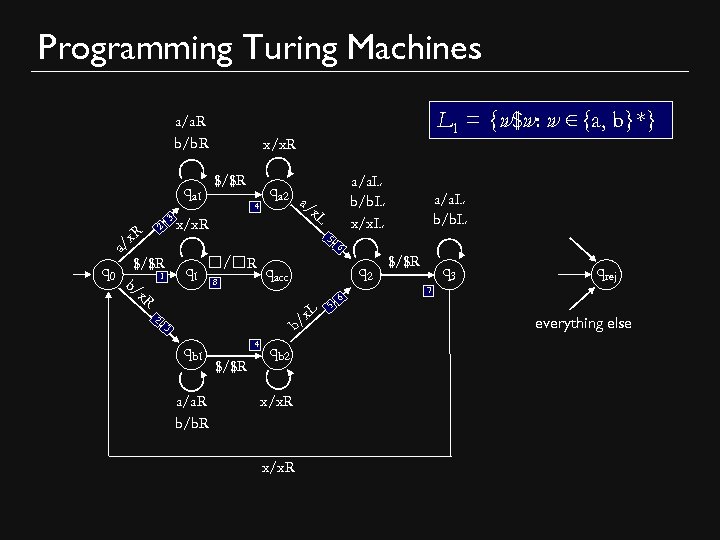Programming Turing Machines a/a. R b/b. R qa 1 3 2 R /x a q 0 $/$R 1 b/ x. R 2 L 1 = {w$w: w ∈{a, b}*} x/x. R $/$R 4 x/x. R a/a. L b/b. L x/x. L qa 2 a /x L 5 6 q 1 ☐/☐R qacc 8 q 2 L /x b 3 qb 1 a/a. R b/b. R 4 $/$R qb 2 x/x. R 5 a/a. L b/b. L 6 $/$R q 3 qrej 7 everything else

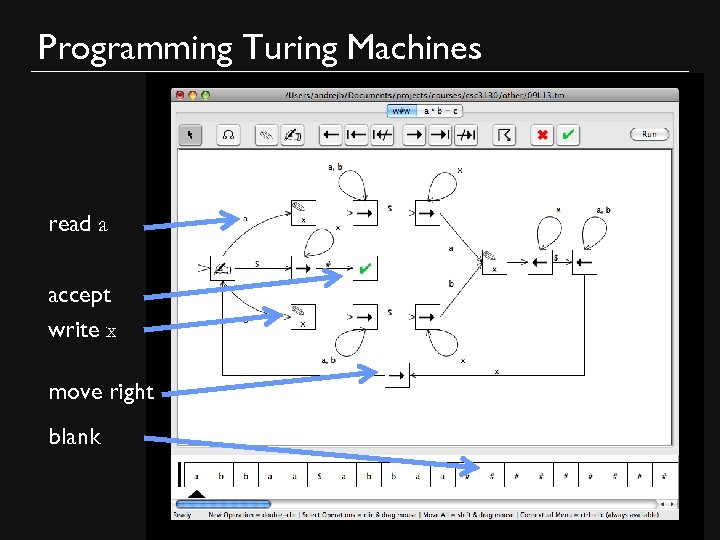Programming Turing Machines read a accept write x move right blank

Programming Turing Machines L 2 = {$aibjck: i × j = k and i, j, k > 0 } Strategy: Scan input from left to right to check it looks like $aa*bb*cc* Move left until you see first a Until all as have been crossed off (x) Cross off one a (x) For every b you see, cross off one of the cs (z) If there are no cs left, reject If there any uncrossed cs left, reject Otherwise, accept

Programming Turing Machines L 2 = {$aibjck: i × j = k and i, j, k > 0 } Implementation detail: For every b you see, cross off one of the cs (z): Until all bs have been crossed off (y) Replace current b by y Move right until you see first c Cross off c (z) Move left until first b Restore the bs: Replace all ys by bs

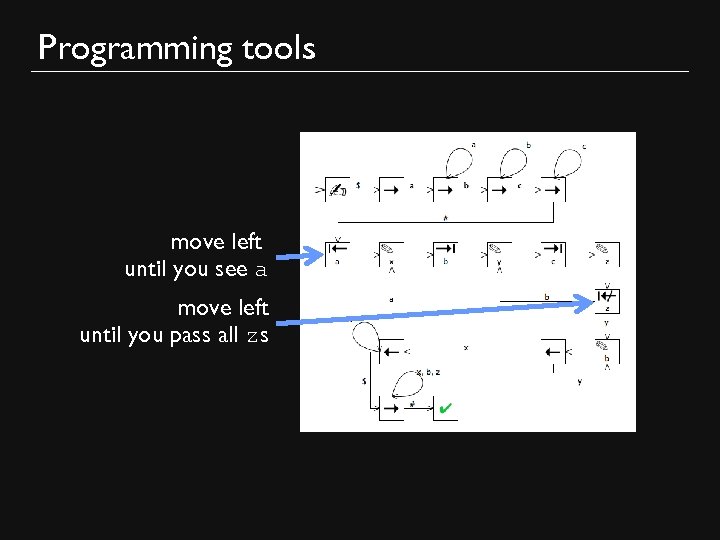Programming tools move left until you see a move left until you pass all zs

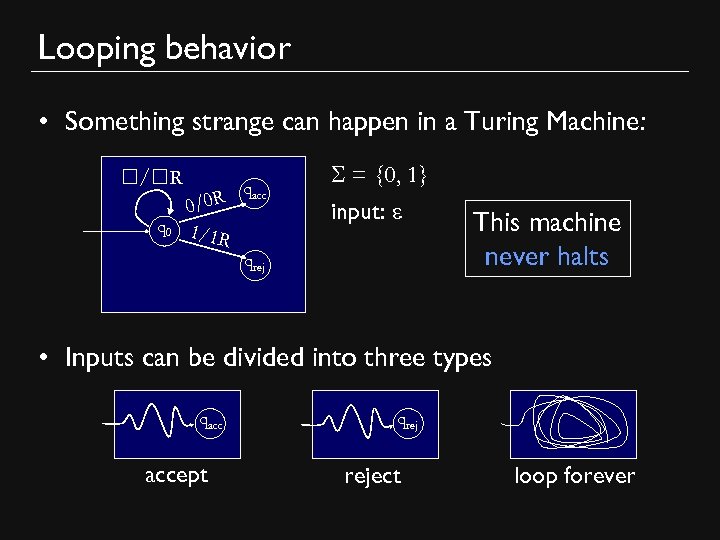Looping behavior • Something strange can happen in a Turing Machine: ☐/☐R q 0 0/0 R 1/1 R qacc = {0, 1} input: e qrej This machine never halts • Inputs can be divided into three types qacc accept qrej reject loop forever

The Church-Turing Thesis Turing Machine quantum computing cosmic computing DNA computing

The Church-Turing Thesis All arguments [for the CT Thesis] which can be given are bound to be, fundamentally, appeals to intuition, and for this reason rather unsatisfactory mathematically. The arguments which I shall use are of three kinds: 1. A direct appeal to intuition 2. A proof of the equivalence of two definitions (In case the new definition has greater intuitive appeal) 3. Giving examples of large classes of numbers which are computable. 1936: “On Computable Numbers, with an Application to the Entscheidungsproblem” Section 9. The extent of the computable numbers