Факультет управления Кафедра экономики и предпринимательства Лекция 7

Факультет управления Кафедра экономики и предпринимательства Лекция 7 -8. Средние величины Зубачев А. Б.

2 Учебные вопросы: 1. Средние величины. 2. Структурные средние.

1. Средние величины - это обобщающие показатели, которые характеризуют типический уровень явлений и выражают величину признака, отнесенную к единице совокупности. Средние величины рассчитываются на основе массовых данных для качественно однородной совокупности. 3

Виды средних величин. -Степенные средние; -Структурные средние (Мода, медиана). 4

Виды степенных средних. 5

Виды степенных средних. 6

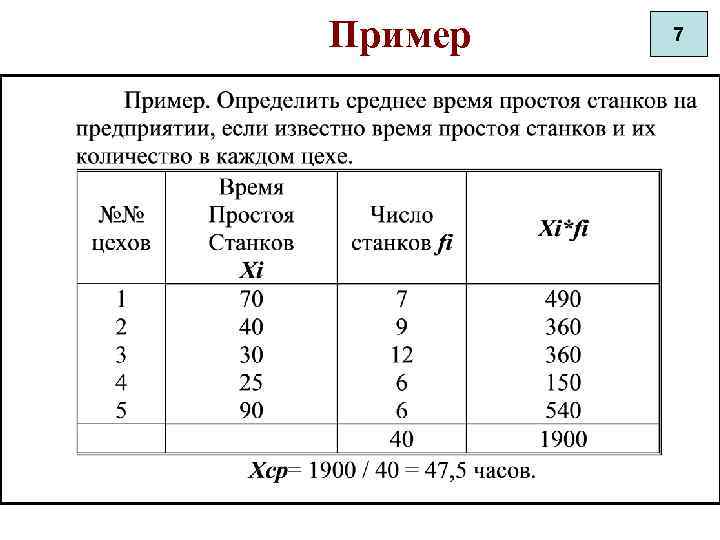Пример 7

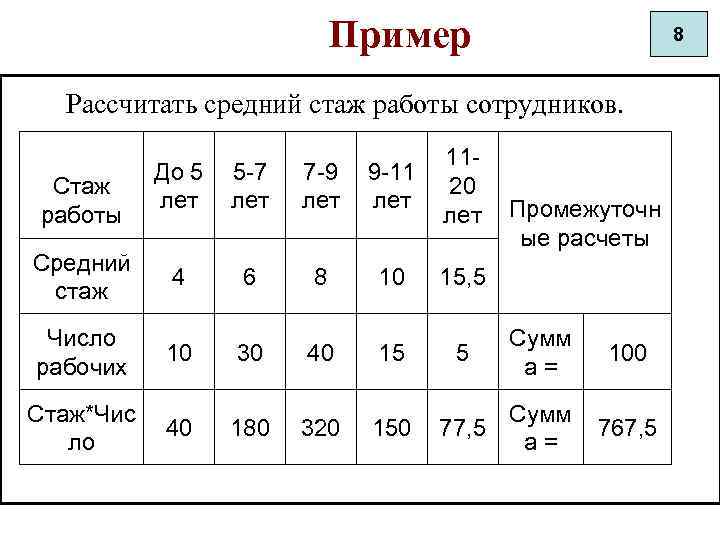Пример 8 Рассчитать средний стаж работы сотрудников. Стаж работы Средний стаж Число рабочих Стаж*Чис ло До 5 лет 5 -7 лет 7 -9 лет 9 -11 лет 1120 лет 4 6 8 10 15, 5 10 40 30 180 40 320 15 150 5 Промежуточн ые расчеты Сумм а= Сумм 77, 5 а= 100 767, 5

Основные свойства средней арифметической 9 1. От уменьшения или увеличения частот каждого значения признака Х в п раз величина средней арифметической не изменится. Если все частоты разделить или умножить на какоелибо число, то величина средней не изменится. 2. Общий множитель индивидуальных значений признака может быть вынесен за знак средней:

Основные свойства средней арифметической 10 3. Средняя суммы (разности) двух или нескольких величин равна сумме (разности) их средних: 4. Если х = с, где с - постоянная величина, то 5. Сумма отклонений значений признака Х от средней арифметической х равна нулю:

Виды степенных средних 11

Средняя гармоническая Наряду со средней арифметической, в статистике применяется средняя гармоническая величина, обратная средней арифметической из обратных значений признака. Как и средняя арифметическая, она может быть простой и взвешенной. 12

Пример Бригада токарей была занята обточкой одинаковых деталей в течение 8 -часового рабочего дня. Первый токарь затратил на одну деталь 12 мин, второй - 15 мин. , третий - 11, четвертый - 16 и пятый - 14 мин. Определите среднее время, необходимое на изготовление одной детали. 13

14 Полученная средняя была бы правильной, если бы каждый рабочий сделал только по одной детали. Но в течение дня отдельными рабочими было изготовлено различное число деталей. Для определения числа деталей, изготовленных каждым рабочим, воспользуемся следующим соотношением: все затраченное время Среднее время, затраченное = -----------------на одну деталь число деталей

15 Число деталей, изготовленных каждым рабочим, определяется отношением всего времени работы к среднему времени, затраченному на одну деталь. Тогда среднее время, необходимое для изготовления одной детали, равно:

Это же решение можно представить иначе: 15 Таким образом, формула для расчета средней гармонической простой будет иметь вид:

Виды степенных средних 16 Свойство мажорантности – с повышением показателя корня от – 1 до 3 значение средней не убывает. Так, если для одной совокупности вычислить все виды степенных средних, то они расположатся в возрастающем порядке. Хгарм <= Xгеом <= Xар <= Xкв <= Xкуб

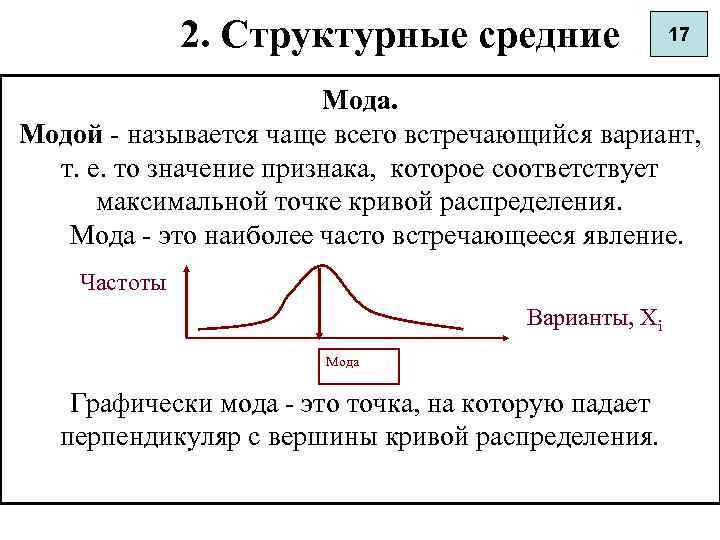2. Структурные средние 17 Мода. Модой - называется чаще всего встречающийся вариант, т. е. то значение признака, которое соответствует максимальной точке кривой распределения. Мода - это наиболее часто встречающееся явление. Частоты Варианты, Xi Мода Графически мода - это точка, на которую падает перпендикуляр с вершины кривой распределения.

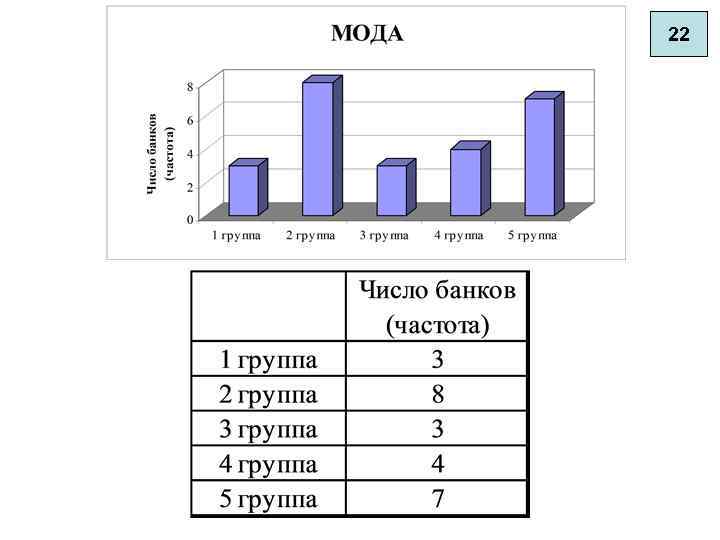
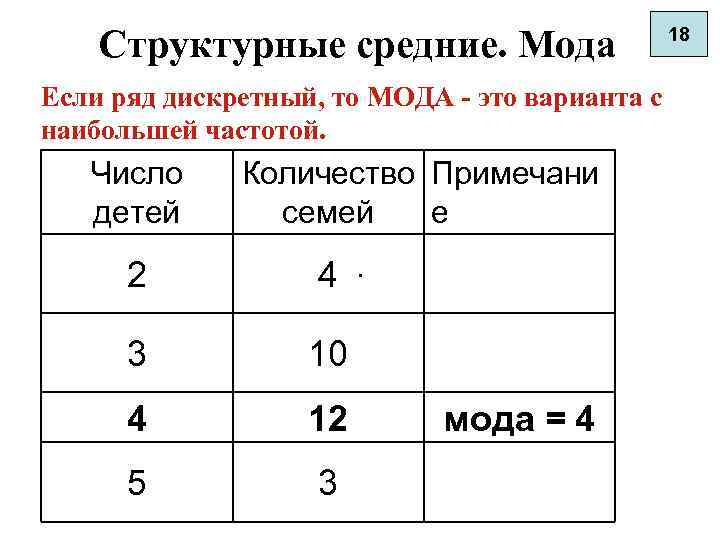Структурные средние. Мода Если ряд дискретный, то МОДА - это варианта с наибольшей частотой. Число детей Количество Примечани семей е 2 4 3 10 4 12 5 3 . мода = 4 18

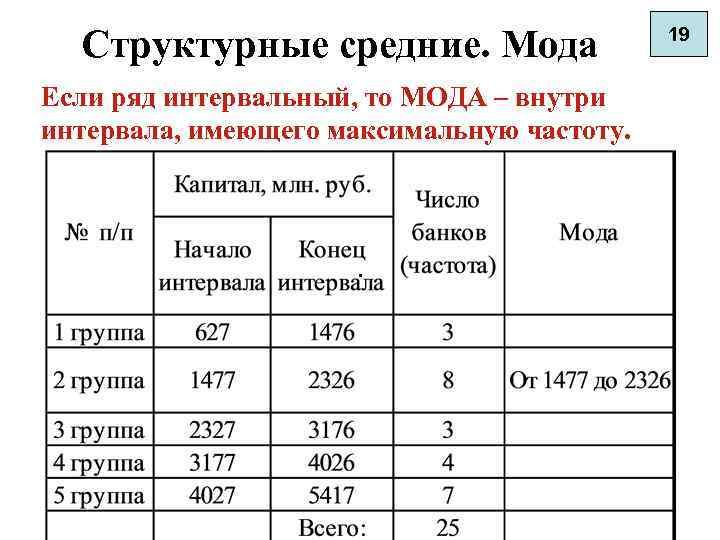Структурные средние. Мода Если ряд интервальный, то МОДА – внутри интервала, имеющего максимальную частоту. . 19

Структурные средние. Мода Если ряд интервальный: По частоте выявляется модальный интервал. Мода находится внутри модального интервала и находится по формуле: где f мо fмо+1 fмо-1 X 2 X 3 Мода Хмо- начало модального интервала; Iмо- величина модального интервала; . fмо-1, fмо+1 - частоты предмодального, модального и послемодального интервала. 20

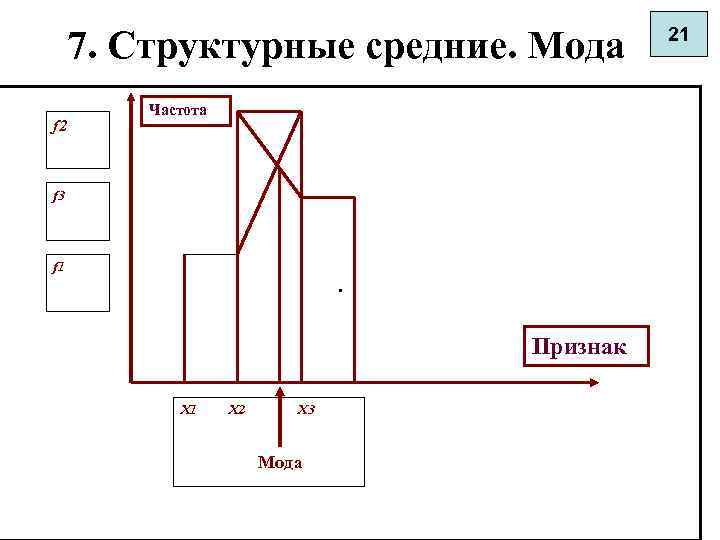7. Структурные средние. Мода f 2 Частота f 3 f 1 . Признак X 1 X 2 X 3 Мода 21

22

Структурные средние. Медиана 23 Медиана - делит площадь гистограммы распределения на две равные. части. Медиана - это величина, которая делит численность упорядоченного вариационного ряда на две равные части.

Структурные средние. Медиана 24 Медиана для дискретного ранжированного ряда, т. е. упорядоченного по возрастанию или убыванию. а) с нечетным числом членов, медианой является центральное значение. Пример. Возраст студентов : 17 18 18 19 20 21 20 Ме = 19 лет. . Хср= (17+18+18+19+20+21+20)/7 = 19, 6 лет. Номер элемента медианы = (n+1)/2. б) При четном числе членов медианой является среднее арифметическое из двух смежных центральных вариант. Для ряда 1 3 4 5 7 9 Ме = (4+5)/2 = 4, 5 Ме = (Хn/2 + X n/2+1)/ 2

7. Структурные средние. Медиана 25 Для интервального ряда: Располагаем варианты по ранжиру. Определяем для ранжированного ряда накопленные частоты. По накопленным частотам находим медианный. интервал, т. е. такой, где накопленная частота больше или равна половине частот. Находим медиану по формуле

Структурные средние. Медиана 26 Для интервального ряда: . Х Mе - нижняя граница варианты медианного интервала IMе - величина медианного интервала fi / 2 - полусумма накопленных частот SМе-1 - накопленные частоты перед медианным интервалом f. Ме - частота медианного интервала

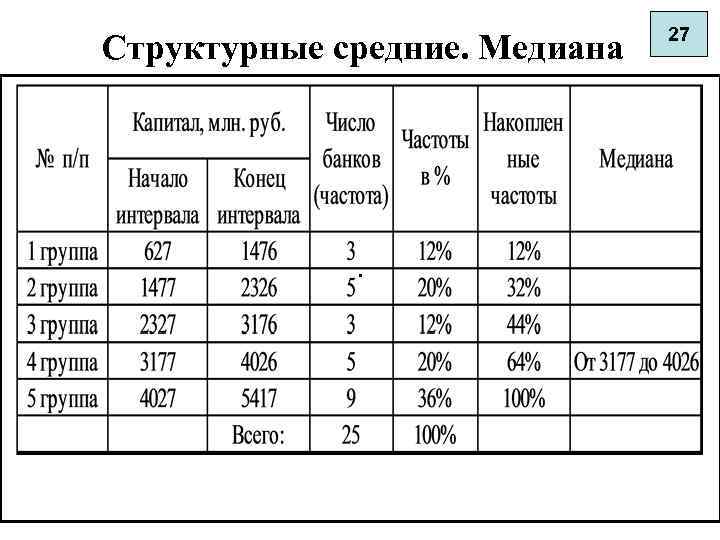Структурные средние. Медиана . 27

Структурные средние. Мода . 28