Факторіал http fallen-souls ucoz ru load 161 У сім ї

Факторіал http: //fallen-souls. ucoz. ru/load/161

У сім'ї - шість чоловік, а за столом в кухні - шість стільців. У сім'ї вирішили кожен вечір, вечеряючи, розсаджуватися на ці шість стільців по-новому. Скільки днів члени сім'ї зможуть робити це без повторень? Для зручності будемо вважати, що сім'я (бабуся, дідусь, мама, тато, дочка, син) буде розсаджуватися по черзі. У бабусі - 6 варіантів вибору стільців. У дідуся - 5 варіантів вибору стільців. У мами - 4 варіанти вибору стільців. У тата - 3 варіанти вибору стільців. У дочки - 2 варіанти вибору стільців. У сина - 1 варіант вибору стільців. За правилом множення: 6 × 5 × 4 × 3 × 2 × 1 = 720 (днів).

Визначення добуток натуральних чисел від одиниці до n включно, позначається n!: n! = 1 × 2 × 3 × 4 ×. . . ×( n - 2) × (n - 1) × n. «factor» - «множник» «Ен факторіал» - «складається з n множників » .

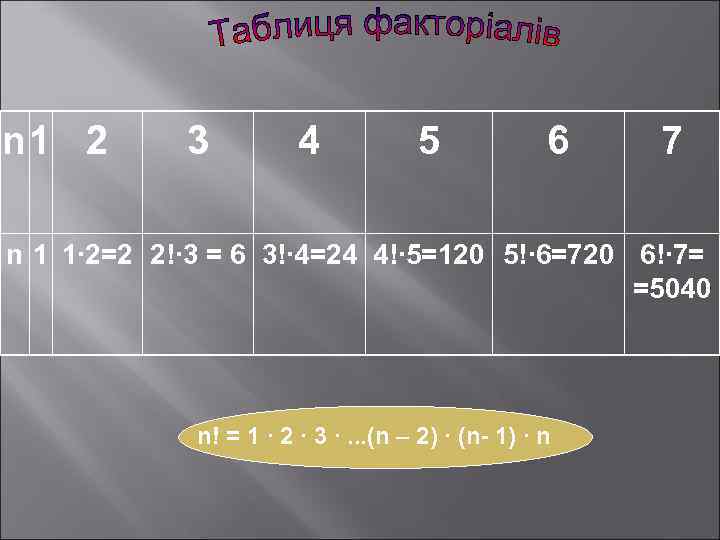n 1 2 3 4 5 6 7 n 1 1∙ 2=2 2!∙ 3 = 6 3!∙ 4=24 4!∙ 5=120 5!∙ 6=720 6!∙ 7= =5040 n! = 1 ∙ 2 ∙ 3 ∙. . . (n – 2) ∙ (n- 1) ∙ n

n! = (n - 1)! ∙ n Приклад: 7! ∙ 4! 6! ∙ 5! 6!∙ 7∙ 4! 6! ∙ 4! ∙ 5 7 5

Приклад: Скількома способами чотири злодія можуть по одному розбігтися на всі чотири сторони? Рішення: Нехай злодії розбігаються по черзі. У першого - 4 варіанти вибору У другого - 3 варіанти вибору У третього - 2 варіанти вибору У четвертого - 1 варіант вибору За правилом множення 4 ∙ 3 ∙ 2 ∙ 1 = 4! = 24 Відповідь: 24 способи.

У 10 класі в середу сім уроків: алгебра, геометрія, література, російська мова, англійська мова, біологія та фізкультура. Скільки можна скласти варіантів розкладу на середу? Для алгебри - 7 варіантів розташування в розкладі Для геометрії - 6 варіантів Для літератури - 5 варіантів і т. д. За правилом множення отримуємо 7 ∙ 6 ∙ 5 ∙ 4 ∙ 3 ∙ 2 ∙ 1 = 7! = 5040

Теорема: n різних елементів можна розставити по одному на n різних місць рівно n! способами. Число всіх перестановок множини з n елементів дорівнює n! Рn = n! Р – перестановки Р 3 = 3! = 6, Р 7 = 7! = 5040.