Fair Division Apportionment Chapters 13 14

Fair Division & Apportionment Chapters 13 & 14 Austin Cole

Fair Division Outline • Adjusted Winner Procedure • Knaster Inheritance Procedure • Taking Turns • Bottom-Up Strategy • Divide and Choose ▫ Steinhaus Proportional Procedure ▫ Banach-Knaster Proportional Procedure ▫ Selfridge-Conway Envy-Free Procedure

Adjusted Winner Procedure • Allows two parties to settle a dispute involving issues or objects with a certain mathematical degree of fairness

Glaxo Wellcome & Smith. Kline Beecham Merger • Assume there were five social issues for compromise: ▫ ▫ ▫ Name of the company Location of headquarters Person to serve as Chairman Person to serve as CEO Where layoffs would come from

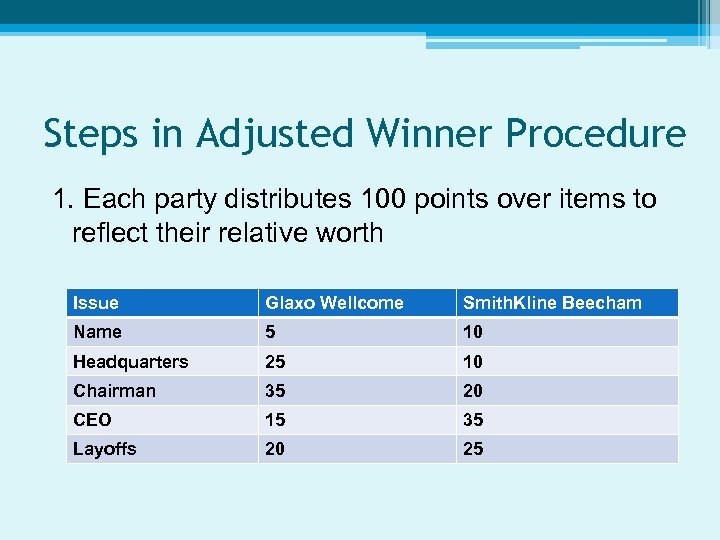Steps in Adjusted Winner Procedure 1. Each party distributes 100 points over items to reflect their relative worth Issue Glaxo Wellcome Smith. Kline Beecham Name 5 10 Headquarters 25 10 Chairman 35 20 CEO 15 35 Layoffs 20 25

2. Each item is given to party that assigned it more points. Each party tallies number of points received. The party with fewest points is given items on which both parties placed the same number of points. Issue Glaxo Smith. Kline Name 5 10 HQ (25) Name (10) HQ 25 10 Chairman (35) CEO (35) Chairman 35 20 CEO 15 35 Layoffs 20 25 Layoffs (25) Points=60 Points=70

3. If point totals aren’t equal, let A denote party with more points and B be the other party. Transfer items from A to B until point totals are equal (can involve fractional transfer). 4. Order is determined by increasing point ratio: A’s point value of the item B’s point value of the item Glaxo Layoffs Point Ratio: 25/20=1. 25 Name Point Ratio: 10/5=2 CEO Point Ratio: 2. 33 Smith. Kline HQ (25) Name (10) Chairman (35) CEO (35) Layoffs (25) Points=60 Points=70

Glaxo Smith. Kline HQ (25) Name (10) Chairman (35) CEO (35) Layoffs (25) Points=60 • • Points=70 So we transfers layoffs, but not the whole value 25 + 35 + 20(1 -X) = 10 + 35 + 25 X X = 7/9 So, 60 + 20(2/9) = 45 + 25(7/9) = 64 Glaxo Smith. Kline HQ (25) Name (10) Chairman (35) CEO (35) 2/9 Layoffs (4) 7/9 Layoffs (19) Points=64

Theorem: Properties of the Adjusted Winner Allocation • Allocation is equitable: both players receive equitable same number of points • Allocation is envy-free: neither player would be envy-free happier with what the other received • Allocation is Pareto-optimal: no other allocation Pareto-optimal can make one party better off without making the other worse off

Knaster Inheritance Procedure • A house has four heirs-Bob, Carol, Ted, & Alice BOB CAROL TED ALICE $120, 000 $200, 000 $140, 000 $180, 000 • Since Carol is the highest bidder, she gets the house ▫ But since her fair-share is ¼, she puts $150 K up for grabs ▫ Each person withdraws ¼ of their bid ▫ Bob: $30 K Ted: $35 K Alice: $45 K ▫ Then the surplus is split four ways

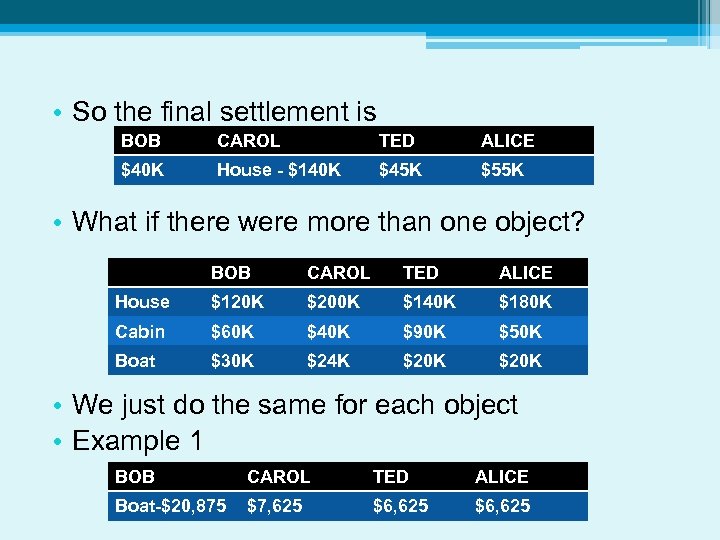• So the final settlement is BOB CAROL TED ALICE $40 K House - $140 K $45 K $55 K • What if there were more than one object? BOB CAROL TED ALICE House $120 K $200 K $140 K $180 K Cabin $60 K $40 K $90 K $50 K Boat $30 K $24 K $20 K • We just do the same for each object • Example 1 BOB CAROL TED ALICE Boat-$20, 875 $7, 625 $6, 625

Taking Turns • How do we decide who chooses first? • Because choosing first is often an advantage, shouldn’t we compensate the other party in some way? • Should a player always choose the object he most favors from those that remain, or are their strategic considerations to take into account?

Dividing up possessions for Divorce Bob’s Ranking Carol’s Ranking Pension House Investments Vehicles House Investments Pension Vehicles 1: Pension 3: Investments 1: House 3: Pension 2: House 4: Vehicles 2: Investments 4: Vehicles

Bottom-Up Strategy Bob Carol A C B E C D D A E B • Rational player will never choose least preferred alternative • Rational player will avoid wasting a choice on an object that he knows will remain available and can be chosen later Bob Carol C A D B E

Divide-and-Choose • http: //www. youtube. com/watch? v=Ad. YFVN 35 h 5 w • One party divides the object into two parts and the other party chooses whichever part he wants

Cake-Division • Cake-Division Procedure: n players allocate a cake among themselves so that each player has a strategy that will guarantee that player a piece with which he is satisfied, even in the face of collusion by others • Procedure is proportional if each player’s strategy guarantees that player a piece of size at least 1/n of the whole in his estimation • Procedure envy-free if each player’s strategy guarantees that player a piece considered to be at least tied for largest

Steinhaus Proportional Procedure for 3 Players • Bob divides a cake into three pieces • Carol & Ted must individually approve a piece to be of size at least 1/3 • Case 1: Carol & Ted approve different pieces. They each get their piece and Bob gets the piece left over. • Case 2: Carol & Ted approve the same piece A and disapprove of piece C. Give Bob piece C. Put A & B back together and let Carol & Ted divide and choose on AB.

Banach-Knaster Proportional Procedure for 4+ Players • Bob cuts a ¼ piece of cake and gives to Carol • If Carol thinks piece is too big, she trims it & places trimmings back on cake & passes piece to Ted • Ted proceeds as Carol did & passes piece to Alice • Alice does the same but then holds on to piece • The piece goes to the last person that trimmed it

• The Bob, Carol, & Alice resume this process with the rest of the cake • Bob cuts a ¼ piece of cake • Carol & Alice each get a chance to trim it and the piece goes to the last person that trimmed it • Final two players use divide -and choose method

Problem with Envy • Both of these proportional procedures are not envy-free • 3 person: What if Carol & Ted both find one piece unacceptable that is given to Bob? • 4+ person: What if Bob receives his first cut piece without any trimmings?

Selfridge-Conway Envy-Free Procedure for 3 Players 1. Player 1 cuts cake into 3 pieces of same size. He hands 3 pieces to player 2. 2. Player 2 trims at most 1 of 3 pieces to create at least 2 -way tie for largest. Set the trimmings aside & hand 3 pieces to player 3. 3. Player 3 chooses a piece 4. Player 2 chooses from 2 remaining pieces. (If he trimmed a piece in step 2 & player 3 didn’t choose it, he must choose it) 5. Player 1 receives remaining piece 6. From trimmings, player 2 cuts into 3 pieces and players choose in order of 3, 1, 2.

Apportionment Outline • • • Hamilton Method Jefferson Method Webster Method Hill-Huntington Method Districts Discussion

Apportionment • Apportionment problem ▫ to round a set of fractions so that their sum is maintained at its original value • Apportionment method ▫ the rounding procedure which must be able to be applied constantly

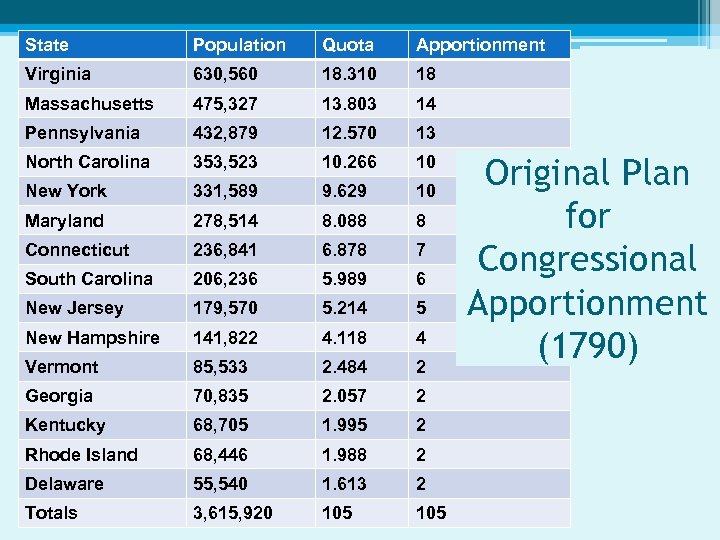State Population Quota Apportionment Virginia 630, 560 18. 310 18 Massachusetts 475, 327 13. 803 14 Pennsylvania 432, 879 12. 570 13 North Carolina 353, 523 10. 266 10 New York 331, 589 9. 629 10 Maryland 278, 514 8. 088 8 Connecticut 236, 841 6. 878 7 South Carolina 206, 236 5. 989 6 New Jersey 179, 570 5. 214 5 New Hampshire 141, 822 4. 118 4 Vermont 85, 533 2. 484 2 Georgia 70, 835 2. 057 2 Kentucky 68, 705 1. 995 2 Rhode Island 68, 446 1. 988 2 Delaware 55, 540 1. 613 2 Totals 3, 615, 920 105 Original Plan for Congressional Apportionment (1790)

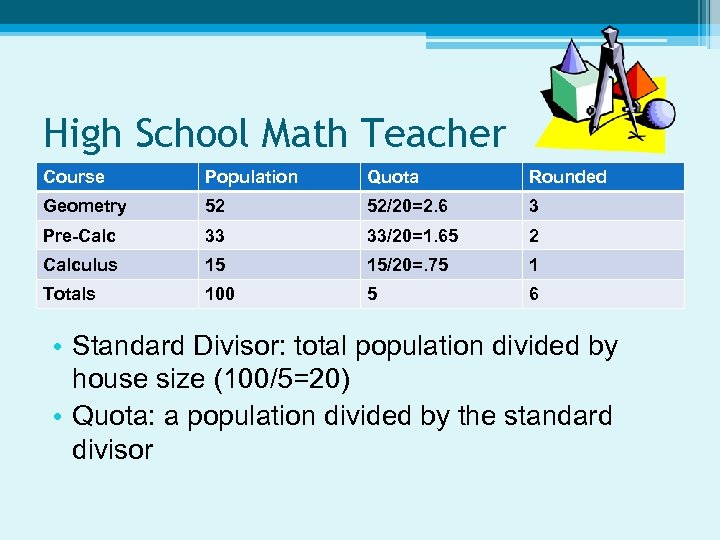High School Math Teacher Course Population Quota Rounded Geometry 52 52/20=2. 6 3 Pre-Calc 33 33/20=1. 65 2 Calculus 15 15/20=. 75 1 Totals 100 5 6 • Standard Divisor: total population divided by house size (100/5=20) • Quota: a population divided by the standard divisor

Hamilton Method • 1. Calculate each state’s quota • 2. Tentatively assign each state its lower quota of representatives. This leaves additional seats. • 3. Allot the remaining seats (one each) to states whose quotas have the largest fractional parts until house is filled

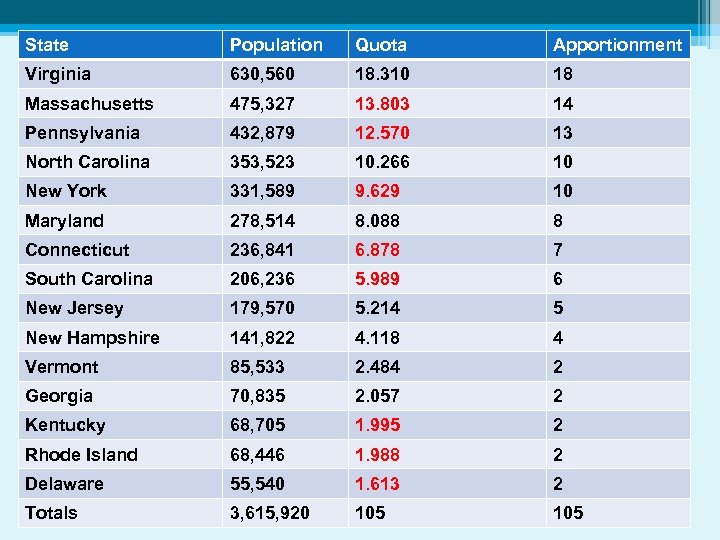State Population Quota Apportionment Virginia 630, 560 18. 310 18 Massachusetts 475, 327 13. 803 14 Pennsylvania 432, 879 12. 570 13 North Carolina 353, 523 10. 266 10 New York 331, 589 9. 629 10 Maryland 278, 514 8. 088 8 Connecticut 236, 841 6. 878 7 South Carolina 206, 236 5. 989 6 New Jersey 179, 570 5. 214 5 New Hampshire 141, 822 4. 118 4 Vermont 85, 533 2. 484 2 Georgia 70, 835 2. 057 2 Kentucky 68, 705 1. 995 2 Rhode Island 68, 446 1. 988 2 Delaware 55, 540 1. 613 2 Totals 3, 615, 920 105

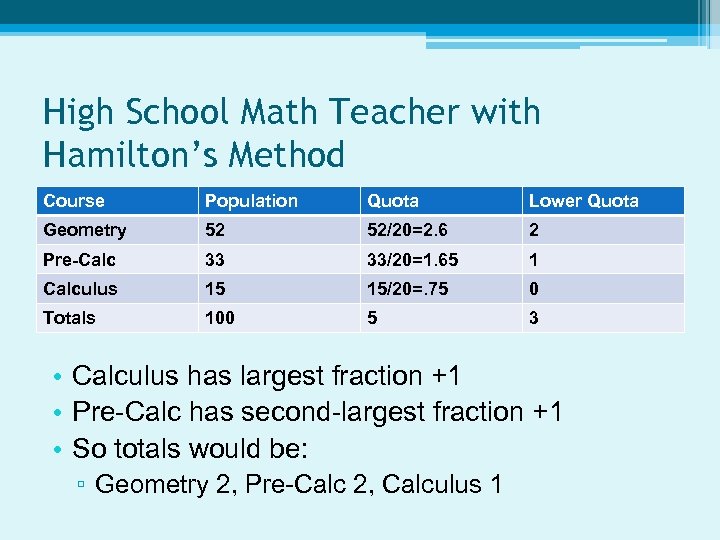High School Math Teacher with Hamilton’s Method Course Population Quota Lower Quota Geometry 52 52/20=2. 6 2 Pre-Calc 33 33/20=1. 65 1 Calculus 15 15/20=. 75 0 Totals 100 5 3 • Calculus has largest fraction +1 • Pre-Calc has second-largest fraction +1 • So totals would be: ▫ Geometry 2, Pre-Calc 2, Calculus 1

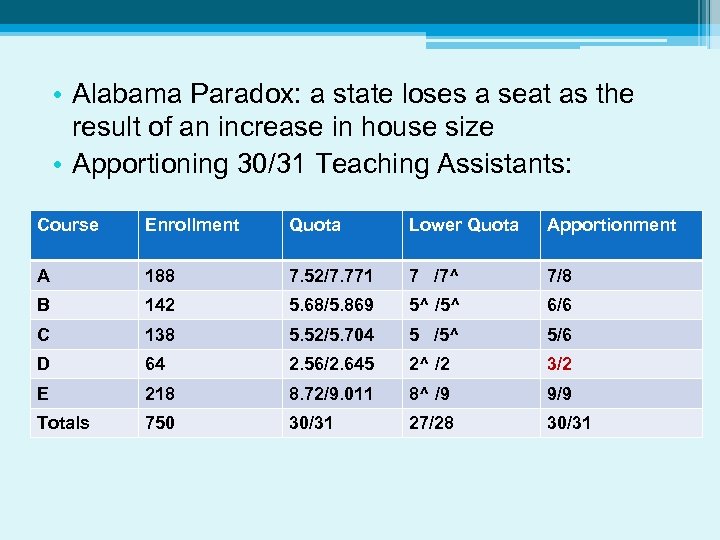• Alabama Paradox: a state loses a seat as the result of an increase in house size • Apportioning 30/31 Teaching Assistants: Course Enrollment Quota Lower Quota Apportionment A 188 7. 52/7. 771 7 /7^ 7/8 B 142 5. 68/5. 869 5^ /5^ 6/6 C 138 5. 52/5. 704 5 /5^ 5/6 D 64 2. 56/2. 645 2^ /2 3/2 E 218 8. 72/9. 011 8^ /9 9/9 Totals 750 30/31 27/28 30/31

Jefferson Method • Divisor method: determines each state’s apportionment by dividing its population by a common divisor d and rounding the quotient • Apportionment for a state i is ▫ Ai = pi rounded down d

Jefferson Method • 1. Determine the standard divisor s and quota qi for each state • 2. Assign each state i its tentative apportionment: ni= pi rounded down s • 3. Find the critical divisor for state i, di= pi ni + 1 • 4. The state with the largest critical divisor receives another seat • 5. If there are extra seats, recompute the critical divisor • 6. When house is filled, the last critical divisor is divisor d, representing the minimum district population

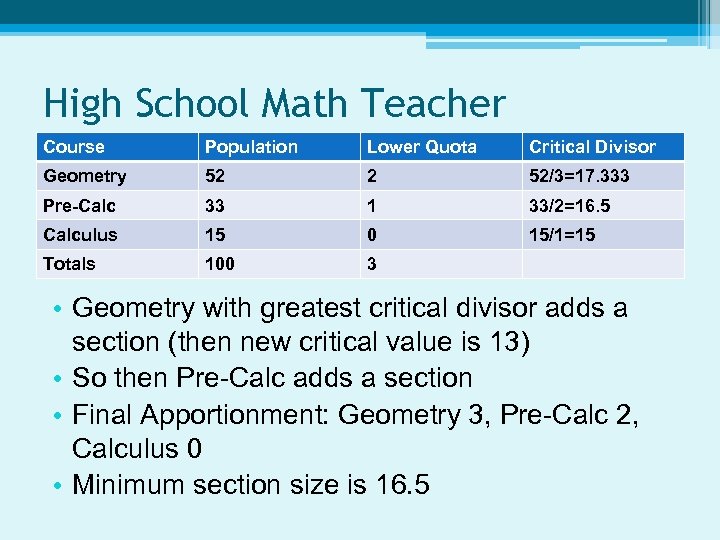High School Math Teacher Course Population Lower Quota Critical Divisor Geometry 52 2 52/3=17. 333 Pre-Calc 33 1 33/2=16. 5 Calculus 15 0 15/1=15 Totals 100 3 • Geometry with greatest critical divisor adds a section (then new critical value is 13) • So then Pre-Calc adds a section • Final Apportionment: Geometry 3, Pre-Calc 2, Calculus 0 • Minimum section size is 16. 5

Hamilton vs. Jefferson Method • 1820 Census: NY Population-1, 368, 775 US Population-8, 969, 878 • House size 213 • Standard divisor = 42, 112 NY’s quota = 32. 503 • Hamilton method→ 33 seats • Jefferson method→ with d=39, 900 ▫ 1, 368, 775/39, 900 rounded down awards 34 seats

Webster Method • The divisor method that rounds the quota to nearest whole number 1. Calculate standard divisor and find each state’s quota 2. The tentative apportionment ni is the rounded quota 3. Calculate sum of tentative apportionments

4. If tentative apportionments don’t fill the house, the critical divisor for state i is di+= pi ni + ½ The state with largest critical divisor receives a seat. 5. If tentative apportionments overfill the house, the critical divisor for state i is di-= pi ni - ½ The state with the smallest critical divisor loses a seat

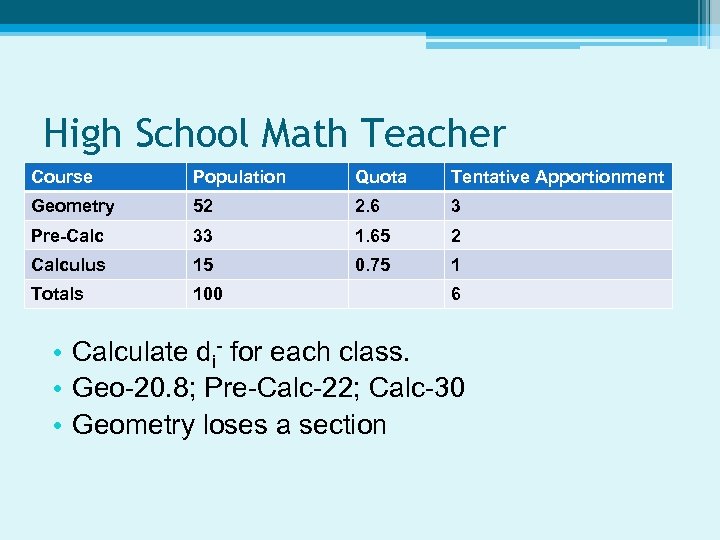High School Math Teacher Course Population Quota Tentative Apportionment Geometry 52 2. 6 3 Pre-Calc 33 1. 65 2 Calculus 15 0. 75 1 Totals 100 6 • Calculate di- for each class. • Geo-20. 8; Pre-Calc-22; Calc-30 • Geometry loses a section

Hill-Huntington Method • Used to apportion House of Reps since 1940 • Find standard divisor and quotas • If quota is greater than geometric mean, round tentative apportionment up • Critical divisor is di± = pi/√ ni(ni± 1) • Exercise 2

Districts • Representative share: apportionment/population • District population: state pop. /apportionment • Relative difference: given positive A, B and A>B, ▫ It is (A-B)/B X 100%

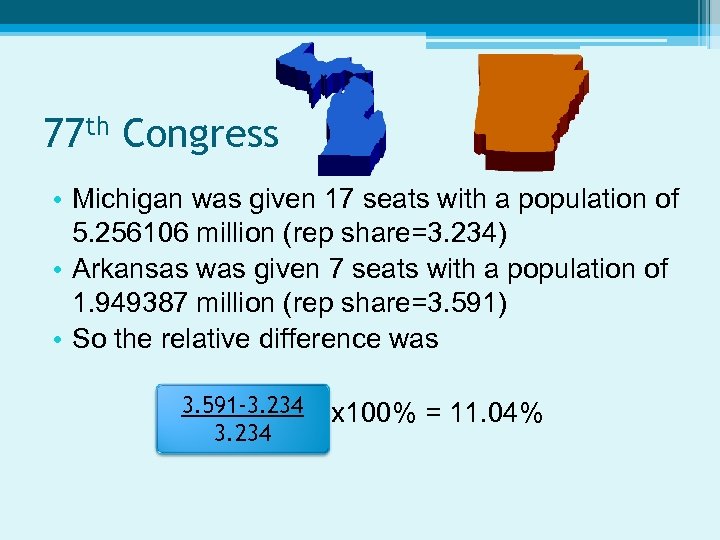77 th Congress • Michigan was given 17 seats with a population of 5. 256106 million (rep share=3. 234) • Arkansas was given 7 seats with a population of 1. 949387 million (rep share=3. 591) • So the relative difference was 3. 591 -3. 234 x 100% = 11. 04%

Discussion • In what instances can you think of that have used proportional procedures? Were they envyfree? • Can you think of other uses for apportionment? Which method would be best? • Homework (7 th Edition) ▫ Chapter 13 #3 ▫ Chapter 14 #19