Factoring Practice 1 x 2 16 x

Factoring Practice 1. x 2 – 16 (x – 4)(x + 4) 2. x 3 + 27 (x + 3)(x 2 - 3 x + 9) 3. 25 x 2 + 15 5(5 x 2 + 3) 4. x 2 – 10 x + 24 (x – 6)(x – 4) 5. 16 x 2 -36 4(2 x – 3)(2 x + 3) 6. 27 x 3 - 8 (3 x – 2)(9 x 2 +6 x + 4)

5. 2 Graphing Simple Rational Functions p. 310 What is the general form of a rational function? What does the h & k tell you? What does the graph of a hyperbola look like? What does the graph of ax+b/cx+d tell you? What information does the domain & range tell you?

Rational Function • A function of the form where p(x) & q(x) are polynomials and q(x)≠ 0.

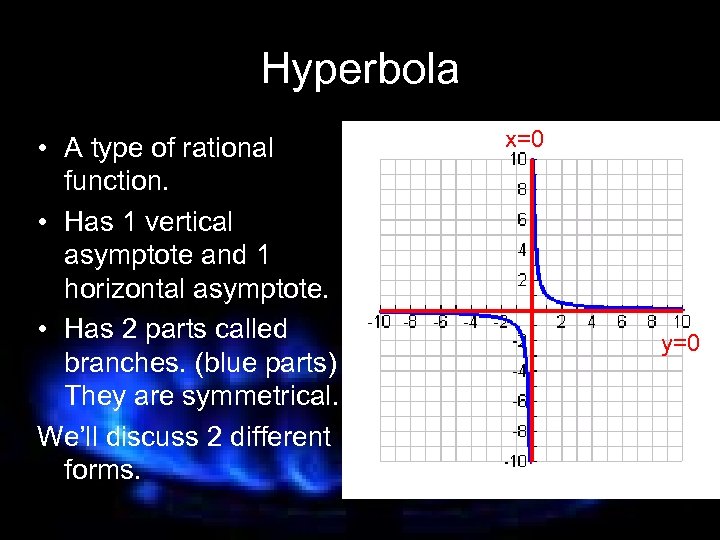Hyperbola • A type of rational function. • Has 1 vertical asymptote and 1 horizontal asymptote. • Has 2 parts called branches. (blue parts) They are symmetrical. We’ll discuss 2 different forms. x=0 y=0

Hyperbola (continued) • One form: • Has 2 asymptotes: x=h (vert. ) and y=k (horiz. ) • Graph 2 points on either side of the vertical asymptote. • Draw the branches.

Hyperbola (continued) • Second form: • Vertical asymptote: Set the denominator equal to 0 and solve for x. • Horizontal asymptote: • Graph 2 points on either side of the vertical asymptote. Draw the 2 branches.

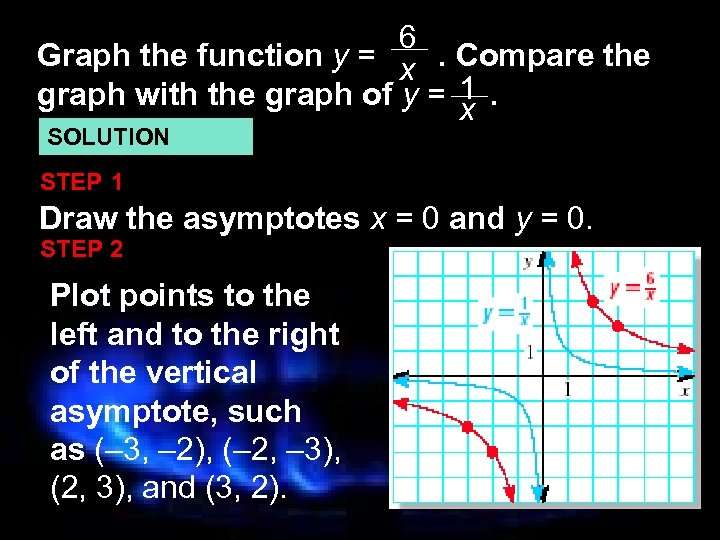6 Graph the function y = x. Compare the graph with the graph of y = 1. x SOLUTION STEP 1 Draw the asymptotes x = 0 and y = 0. STEP 2 Plot points to the left and to the right of the vertical asymptote, such as (– 3, – 2), (– 2, – 3), (2, 3), and (3, 2).

STEP 3 Draw the branches of the hyperbola so that they pass through the plotted points and approach the asymptotes. 6 The graph of y = x lies farther from the 1. axes than the graph of y = x Both graphs lie in the first and third quadrants and have the same asymptotes, domain, and range.

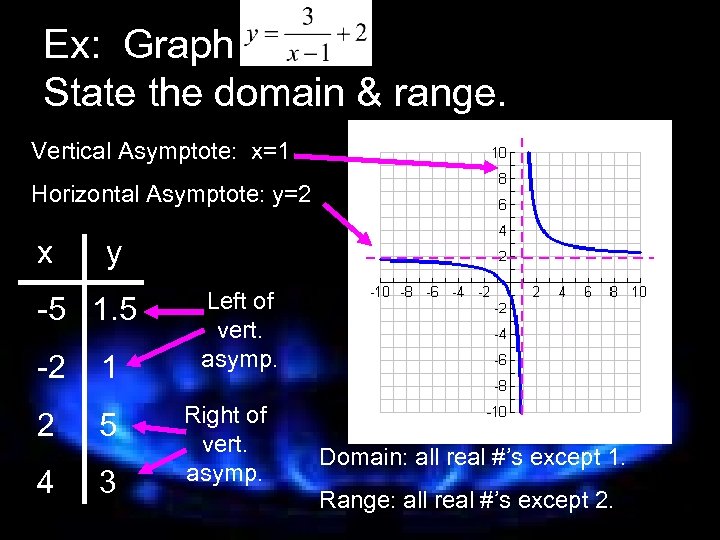Ex: Graph State the domain & range. Vertical Asymptote: x=1 Horizontal Asymptote: y=2 x y -5 1. 5 -2 1 2 5 4 3 Left of vert. asymp. Right of vert. asymp. Domain: all real #’s except 1. Range: all real #’s except 2.

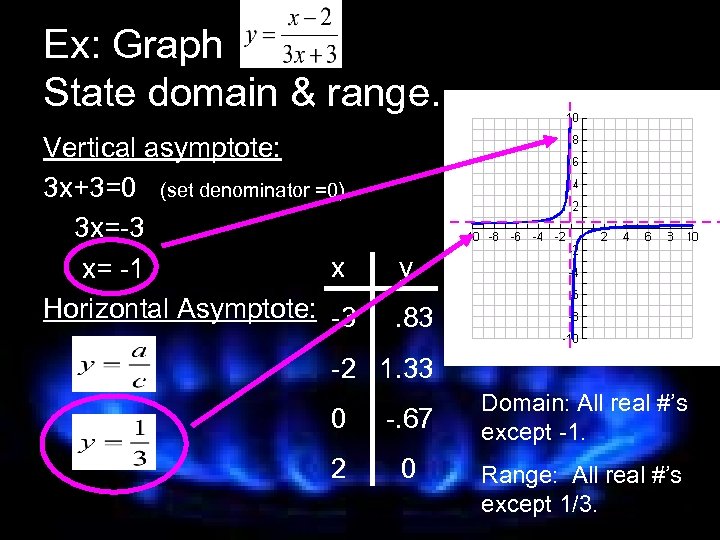Ex: Graph State domain & range. Vertical asymptote: 3 x+3=0 (set denominator =0) 3 x=-3 x y x= -1 Horizontal Asymptote: -3 . 83 -2 1. 33 0 -. 67 2 0 Domain: All real #’s except -1. Range: All real #’s except 1/3.

3 -D Modeling A 3 -D printer builds up layers of material to make three dimensional models. Each deposited layer bonds to the layer below it. A company decides to make small display models of engine components using a 3 -D printer. The printer costs $24, 000. The material for each model costs $300. • Write an equation that gives the average cost per model as a function of the number of models printed.

• Graph the function. Use the graph to estimate how many models must be printed for the average cost per model to fall to $700. • What happens to the average cost as more models are printed? SOLUTION STEP 1 Write a function. Let c be the average cost and m be the number of models printed. Unit cost • Number printed + Cost of printer c= Number printed 300 m + 24, 000 = m

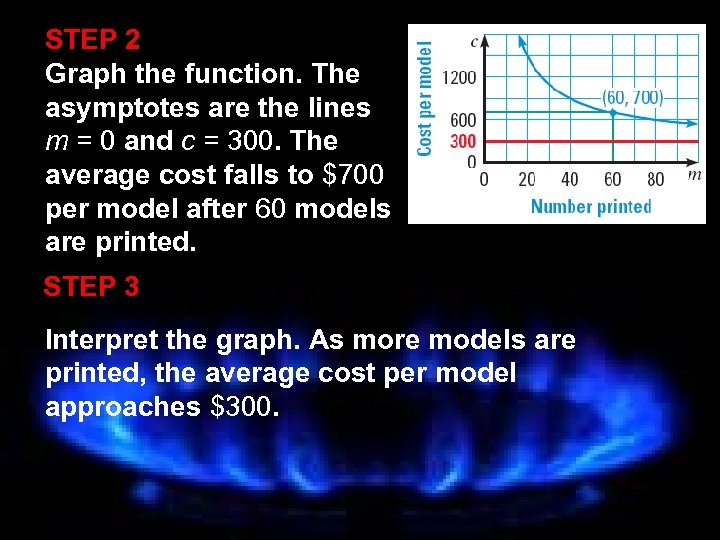STEP 2 Graph the function. The asymptotes are the lines m = 0 and c = 300. The average cost falls to $700 per model after 60 models are printed. STEP 3 Interpret the graph. As more models are printed, the average cost per model approaches $300.

Graph the function. State the domain and range. x – 1 4. y = x + 3 SOLUTION ANSWER domain: all real numbers except – 3, range: all real numbers except 2.

• What is the general form of a rational function? • What does the h & k tell you? Asymptotes are x = h, y = k • What does the graph of a hyperbola look like? Two symmetrical branches in opposite quadrants. • What does the graph of ax+b/cx+d tell you? cx+d = 0 is the vertical asymptote and y = a/c is the horizontal asymptote • What information does the domain & range tell you? Domain tells what numbers can be used for x and the range is the y numbers when put into the equation.

Assignment p. 313, 6 -8, 14 -20, 28 -31