Face Recognition Sumitha Balasuriya Computer Vision

Face Recognition Sumitha Balasuriya

Computer Vision • Image processing is a precursor to Computer Vision – making a computer understand interpret what’s in an image or video. 3 D shape Robotics Recognition Tracking Categorisation / Retrieval Segmentation

Innate Face Recognition Ability • Face recognition almost instantaneous • Highly invariant to pose, scale, rotation, lighting changes • Can handle partial occasions and changes in age • And we can do all this for faces of several thousand individuals Who is this?

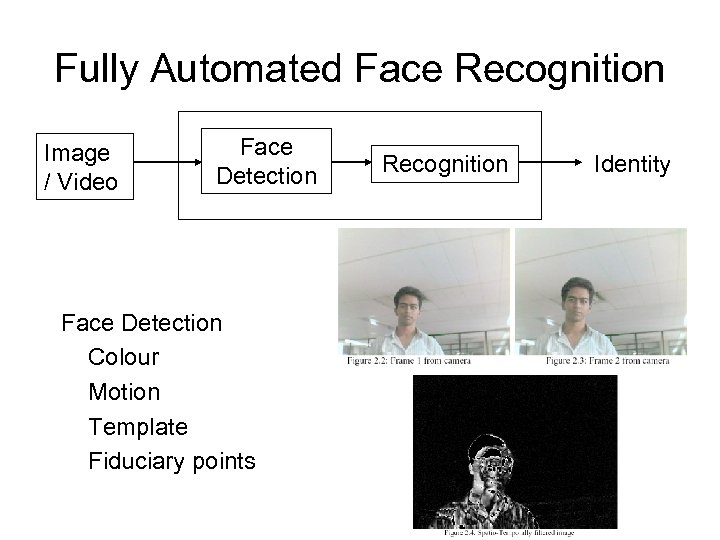
Fully Automated Face Recognition Image / Video Face Detection Colour Motion Template Fiduciary points Recognition Identity

Face Detection Australian National University Detect face and facial landmarks Register (align) face using an image transform

Face Recognition approaches Geometric features Recognition possible at low resolution and at high noise levels because geometrical features such as nose width and eye separation are used Automated extraction of facial geometric features is very hard Template matching Extract facial regions (matrix of pixels) and compare with that of known individuals Need templates for different face poses/views Very high dimensional data

High Dimensional Correlated Data • Images as a high dimensional vector • A typical image used for image processing will be 512 x 512= 262144 dimension vector! I • (Registered) face images are highly correlated I Face images 1, 2 …. I 1, 1 Image space (high dimensional space of all possible images)

Transform Face images to a ‘Face Space’ Face space (low dimensional space of face images) Face images U 2 • The basis vectors (Ui) of face space are the Principal Components of face images. U 3 • These Principal Components (PCs) correspond to the directions of U 1 greatest variation of the face dataset. • The first PC corresponds to the direction (and scale) of greatest variation, the 2 nd PC corresponds to the orthogonal direction with the second greatest variation and so on … • Embedding a face image vector into face space is done by calculating the vector’s projection onto the Principal Components. Mean face image f = U * (I - A) Embedded face Face image Eigenfaces Change dimensionality of f by changing that of U

Principal Component Analysis (Karhunen-Loeve transform) • PCA – find the Principal Components of a dataset • Finding the Eigenvectors and eigenvalues of the covariance matrix (Eigen decomposition) • The covariance matrix contains the relationships (correlations) between the variables of the vectors. Variances along the diagonals and covariance between each pair of variables in other positions

PCA (continued) Covariance matrix for images For images will run out of memory because for a dataset of say 512 x 512 images X*XT will be a 262144 x 262144 matrix. If it has double precision (64 bit) values C will be 512 GB!!! Therefore for image we instead compute the reduced covariance matrix If we have n datapoints c will be nxn. As n is normally much smaller than the dimensionality of the images the matrix c is computable Find the Eigenvectors and eigenvalues of c, solve the following linear equations You can get Matlab to solve equations to give the eigenvectors Eigenvalues and eigenvalues Reduced (degree of covariance Eigenvectors variation) >> [V, lamda]=eig(c); matrix (Principal Compoments!!)

PCA (continued) Eigenvectors (Eigenfaces) of covariance matirx Another way to compute PCA – Singular Value Decomposition method Don’t need to compute covariance matrix SVD decomposes an mxn matrix X to a product X = U * S * VT Left singular vectors (eigenvectors of X*XT) Diagonal matrix with eigenvalues along diagonal You can get Matlab to solve these equations as well to get U, S and V Right singular vectors >> [U, S, V]=svd(X); (eigenvectors of XT*X) Use eigen decomposition with the reduced covariance matrix if you run out of memory with svd (seems to work upto 100 x 100 images)

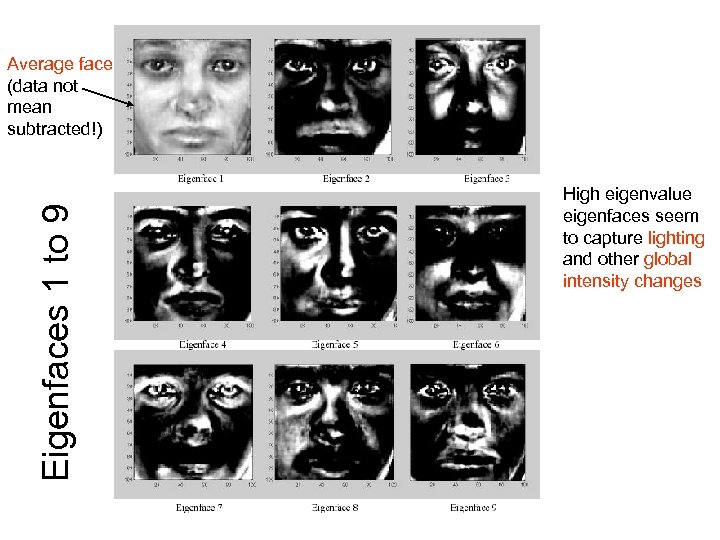
Eigenfaces 1 to 9 Average face (data not mean subtracted!) High eigenvalue eigenfaces seem to capture lighting and other global intensity changes

Eigenfaces 10 to 18 Lower eigenvalue eigenfaces are better for recognition

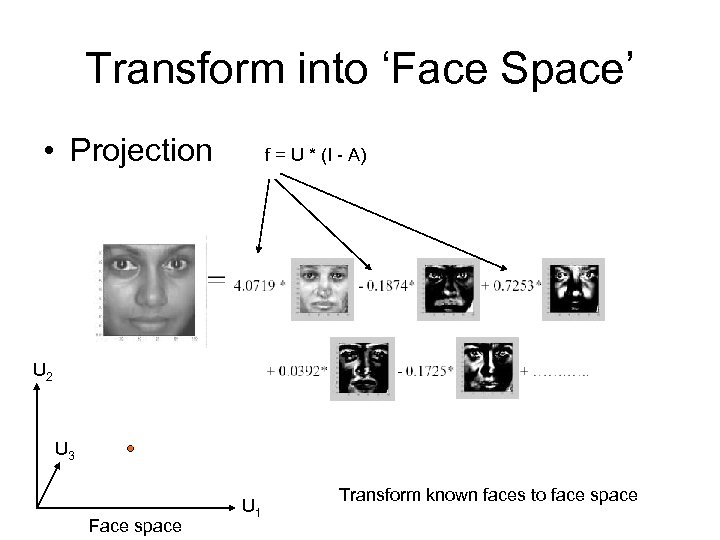
Transform into ‘Face Space’ • Projection f = U * (I - A) U 2 U 3 Face space U 1 Transform known faces to face space

Reconstruction F = UT * U * (I - A) Transform back to image space Mean subtracted image Transform to face space Very high compression! Face space with 28 eigenvectors 100 x 8 bits = 10000 bytes compress to 28*32 bits=112 bytes Only compress faces Can know whether image contains a face by calculating reconstruction error Face detection method!

Classifiers Classify an unknown face into one of the ? known face classes Important concepts • Inter-class (between-class) variance • Intra-class (within-class) variance Need a metric to measure distance for class membership

Metric A non-negative function g(x, y) describing the "distance" between neighbouring points for a given set and satisfies (1) g(x, y)+g(y, z)≥g(x, z) (triangle inequality) (2) g(x, y)=g(y, x) (symmetry) (3) g(x, x)=0, as well as g(x, y)=0 x=y

Euclidean distance (~300 BC) Decision surface Mahalanobis distance (1936) Superior to Euclidean distance because it takes distribution of the points (correlations) into account The distance between two N dimensional points scaled by the statistical variation in each component of the point.

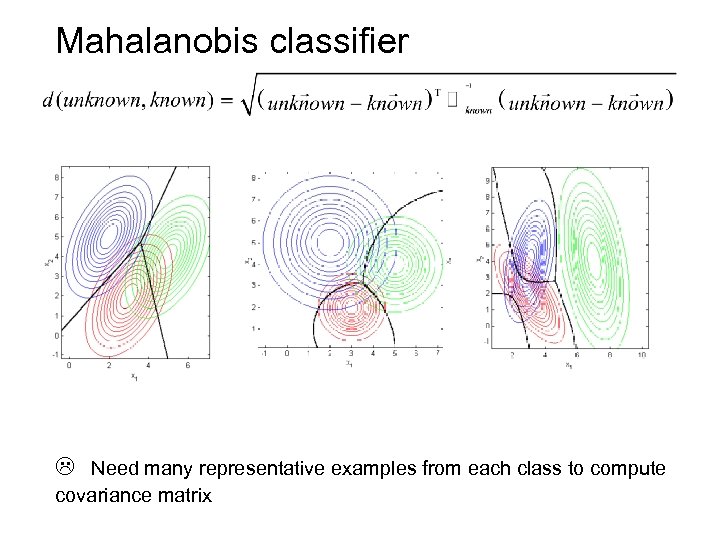
Mahalanobis classifier Need many representative examples from each class to compute covariance matrix

Recap • • Image processing precursor to Computer Vision Face Detection Images are high dimensional correlated data Principal Component Analysis – Eigen decomposition – Singular Value Decomposition • Eigenfaces for recognition, compression, face detection • Classifiers and Metrics

Questions • Will performance improve if we used orientated edge responses of the face image for recognition? Why? • A popular approach uses orientated responses only from certain specific points on the face image (say edge of nose, sides of eyes). What are the advantages/disadvantages of this approach? • PCA maximises the variance between vectors embedded in the eigenspace. What does LDA (Linear Discriminant Analysis) do?