f x f x 0 x x 0 x

f(x) f(x 0) x x 0 x

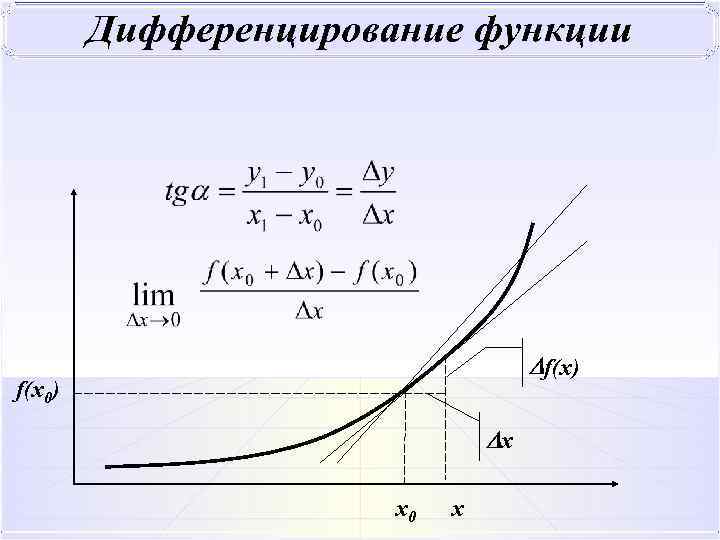
Разностное отношение может иметь конечный предел в точке x 0 только при условии, что y→ 0 при x→ 0 , т. е. в точке x 0 функция y=y(x) непрерывна, но обратное утверждение в общем случае не выполняется.

• В частности, это относится к случаям т. н. острых экстремумов y y=|x| x

Дифференцирование функции

Дифференцирование функции

Правила дифференцирования

Таблица производных

Производная сложной функции и Пример

Дифференциал функции Дифференциалом dy функции y=f(x) в точке x 0 называется главная, линейная относительно x, часть приращения функции в этой точке. dy=f’(x) x=f’(x)dx y=dy+ x, где - бесконечно малая функция при x→ 0 y dy x

Приближенные вычисления. Пример. Вычислить .

Теорема Ферма Если функция y=f(x) дифференцируема в точке а, т. е. существует f’(a) , и всюду в некоторой окрестности этой точки f(x)f(a)) , т. е. f(a) является наибольшим (наименьшим) значением функции в этой окрестности, то f’(a)=0

Теорема Ролля Если функция y=f(x) непрерывна на отрезке [a, b], дифференцируема на интервале (a, b) и f(a)=f(b), то в некоторой точке интервала c (a, b) ее производная равна нулю.

Теорема Лагранжа Если функция y=f(x) непрерывна на отрезке [a, b], дифференцируема на интервале (a, b), то найдется точка c (a, b) для которой f(b)-f(a)=(b–a)f'(c)

Теорема Коши Если функции f(x) и g(x) определены и непрерывны на отрезке [a, b], дифференцируемы на интервале (a, b) и при этом g(x)≠ 0, то найдется точка c (a, b) для которой

Если 1. или 2. Существует конечный или бесконечный Тогда

Производные и дифференциалы высших порядков Если функция f(x), определенная в А, имеет производную во всех точках А, то эту производную можно рассматривать как новую функцию g(x)=f’(x), x A. К этой функции применимы все предельные законы, в том числе и дифференцирование. Если g(x), определенная в А, имеет конечную производную g’(x) в точке x A, то значение этой производной является второй производной функции f(x). Аналогично вычисляются производные более высоких порядков.

План исследования функции и построения ее графика 1. Найти область определения 2. Исследовать на четность, нечетность, периодичность 3. Найти точки разрыва функции и определить их классификацию 4. Исследовать на наличие асимптот 5. Определить интервалы знакопостоянства функции 6. С помощью производной найти интервалы возрастания, убывания функции и ее экстремумы 7. С помощью производной второго порядка найти интервалы выпуклости, вогнутости функции и точки перегиба 8. Найти значения (или пределы) функции в граничных точках ее области определения

Исследовать функцию и построить график: 1. Найти область определения 2. Исследовать на четность, нечетность, периодичность Функция нечетна, непериодична 3. Найти точки разрыва функции и определить их классификацию Точек разрыва нет

Исследовать функцию и построить график: 4. Исследовать на наличие асимптот При x y 0; x y 0 - ось x - асимптота 5. Определить интервалы знакопостоянства функции

Исследовать функцию и построить график: 6. С помощью производной найти интервалы возрастания, убывания функции и ее экстремумы x = 1 и x = – 1 -- точки локальных экстремумов

Исследовать функцию и построить график: 7. С помощью производной второго порядка найти интервалы выпуклости, вогнутости функции и точки перегиба

Исследовать функцию и построить график: x ( – – ) – 1 (– 1; 0) 0 (0; 1) 1 1; ) ( ; y'(x) – – – 0 + + + 0 – – – y''(x) – 0 + + + 0 – – – 0 + min точка перегиба max точка перегиба

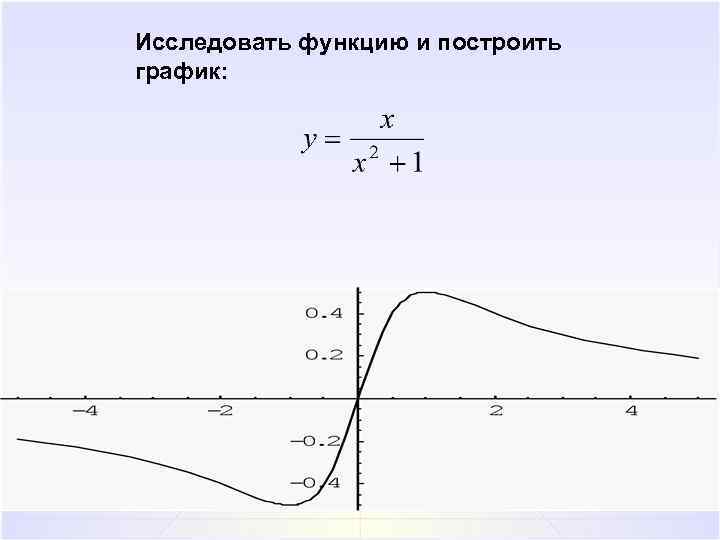Исследовать функцию и построить график:

Исследовать функцию и построить график: 1. Найти область определения 2. Исследовать на четность, нечетность, периодичность Функция не является периодической, четной, нечетной. 3. Найти точки разрыва функции и определить их классификацию точка разрыва (точка бесконечного скачка).

Исследовать функцию и построить график: 4. Исследовать на наличие асимптот При x 0 прямая y ось y - асимптота является двусторонней наклонной асимптотой. 5. Определить интервалы знакопостоянства функции

Исследовать функцию и построить график: 6. С помощью производной найти интервалы возрастания, убывания функции и ее экстремумы x = 1 и x = – 1 -- точки локальных экстремумов

Исследовать функцию и построить график: 7. С помощью производной второго порядка найти интервалы выпуклости, вогнутости функции и точки перегиба

Исследовать функцию и построить график: x (- , -2) -2 (-2, 0) y (x) + 0 y (x) возраст ает y(x) (0, 1) 1 (1, + ) - + 0 + - - - 0 + лок. макс. убывае т переги б выпукла вниз выпукла вверх 0 бескон ечный скачок возрастает выпукла вверх

Исследовать функцию и построить график: