F ra n k C o w






















- Размер: 821.5 Кб
- Количество слайдов: 45
Описание презентации F ra n k C o w по слайдам
 F ra n k C o w e ll: M ic ro e c o n o m ic s Risk MICROECONOMICS Principles and Analysis Frank Cowell Almost essential Consumption and Unce rtainty. Prerequisites November
F ra n k C o w e ll: M ic ro e c o n o m ic s Risk MICROECONOMICS Principles and Analysis Frank Cowell Almost essential Consumption and Unce rtainty. Prerequisites November
 F ran k C o w ell: M icro eco n o m ics Risk and uncertainty In dealing with uncertainty a lot can be done without introducing probability. Now we introduce a specific probability model This could be some kind of exogenous mechanism Could just involve individual’s perceptions Facilitates discussion of risk Introduces new way of modelling preferences
F ran k C o w ell: M icro eco n o m ics Risk and uncertainty In dealing with uncertainty a lot can be done without introducing probability. Now we introduce a specific probability model This could be some kind of exogenous mechanism Could just involve individual’s perceptions Facilitates discussion of risk Introduces new way of modelling preferences
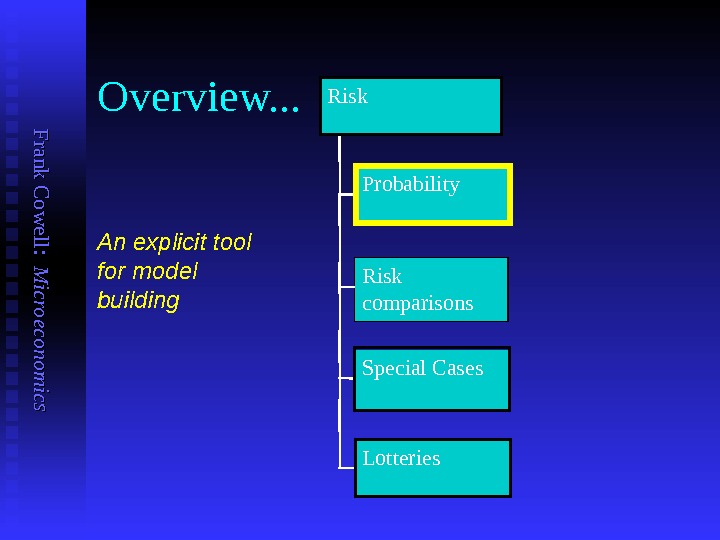
 F ran k C o w ell: M icro eco n o m ics Overview. . . Probability Risk comparisons Special Cases Lotteries. Risk An explicit tool for model building
F ran k C o w ell: M icro eco n o m ics Overview. . . Probability Risk comparisons Special Cases Lotteries. Risk An explicit tool for model building
 F ran k C o w ell: M icro eco n o m ics Probability What type of probability model? A number of reasonable versions: Public observable Public announced Private objective Private subjective Need a way of appropriately representing probabilities in economic models. Lottery government policy? coin flip emerges from structure of preferences.
F ran k C o w ell: M icro eco n o m ics Probability What type of probability model? A number of reasonable versions: Public observable Public announced Private objective Private subjective Need a way of appropriately representing probabilities in economic models. Lottery government policy? coin flip emerges from structure of preferences.
 F ran k C o w ell: M icro eco n o m ics Ingredients of a probability model We need to define the support of the distribution The smallest closed set whose complement has probability zero Convenient way of specifying what is logically feasible (points in the support) and infeasible (other points). Distribution function FF Represents probability in a convenient and general way. Encompass both discrete and continuous distributions. Discrete distributions can be represented as a vector Continuous distribution – usually specify density function Take some particular cases: a collection of examples
F ran k C o w ell: M icro eco n o m ics Ingredients of a probability model We need to define the support of the distribution The smallest closed set whose complement has probability zero Convenient way of specifying what is logically feasible (points in the support) and infeasible (other points). Distribution function FF Represents probability in a convenient and general way. Encompass both discrete and continuous distributions. Discrete distributions can be represented as a vector Continuous distribution – usually specify density function Take some particular cases: a collection of examples
 F ran k C o w ell: M icro eco n o m ics Some examples Begin with two cases of discrete distributions ## = 2. Probability of value xx 00 ; probability 1 –– of of value xx 11. . ## = 5. Probability ii of value xxii , , ii = 0, . . . , 44. . Then a simple example of continuous distribution with bounded support The rectangular distribution – – uniform density over an interval. Finally an example of continuous distribution with unbounded support
F ran k C o w ell: M icro eco n o m ics Some examples Begin with two cases of discrete distributions ## = 2. Probability of value xx 00 ; probability 1 –– of of value xx 11. . ## = 5. Probability ii of value xxii , , ii = 0, . . . , 44. . Then a simple example of continuous distribution with bounded support The rectangular distribution – – uniform density over an interval. Finally an example of continuous distribution with unbounded support
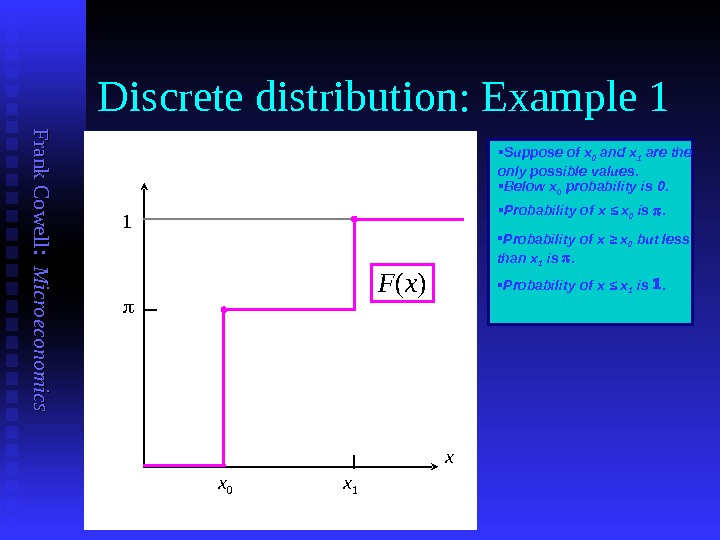
 F ran k C o w ell: M icro eco n o m ics Discrete distribution: Example 1 x Below x 0 probability is 0. Probability of x ≤ x 0 is . x 1 x 01 Probability of x ≤ x 1 is . Suppose of x 0 and x 1 are the only possible values. F ( x ) Probability of x ≥ x 0 but less than x 1 is .
F ran k C o w ell: M icro eco n o m ics Discrete distribution: Example 1 x Below x 0 probability is 0. Probability of x ≤ x 0 is . x 1 x 01 Probability of x ≤ x 1 is . Suppose of x 0 and x 1 are the only possible values. F ( x ) Probability of x ≥ x 0 but less than x 1 is .
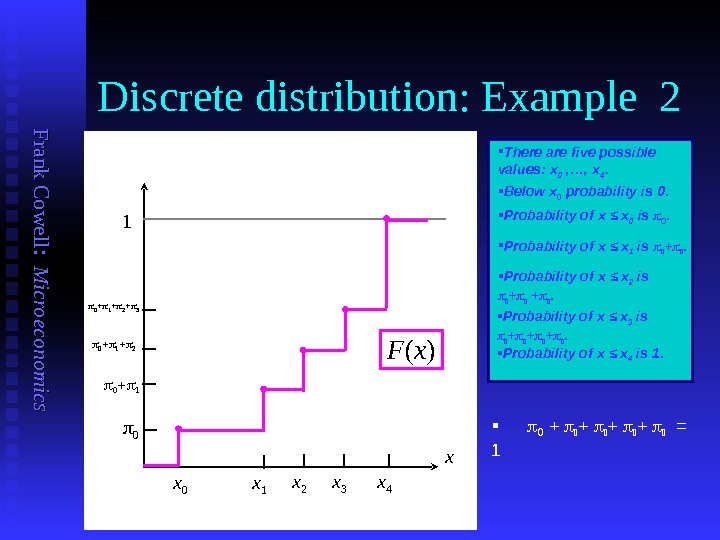
 F ran k C o w ell: M icro eco n o m ics Discrete distribution: Example 2 x Below x 0 probability is 0. Probability of x ≤ x 0 is . x 1 x 01 0 Probability of x ≤ x 1 is + . There are five possible values: x 0 , …, x 4. F ( x ) 0 1 2 3 Probability of x ≤ x 2 is + + . x 4 x 2 x 3 0 1 2 Probability of x ≤ x 3 is + + + . Probability of x ≤ x 4 is 1. + + =
F ran k C o w ell: M icro eco n o m ics Discrete distribution: Example 2 x Below x 0 probability is 0. Probability of x ≤ x 0 is . x 1 x 01 0 Probability of x ≤ x 1 is + . There are five possible values: x 0 , …, x 4. F ( x ) 0 1 2 3 Probability of x ≤ x 2 is + + . x 4 x 2 x 3 0 1 2 Probability of x ≤ x 3 is + + + . Probability of x ≤ x 4 is 1. + + =
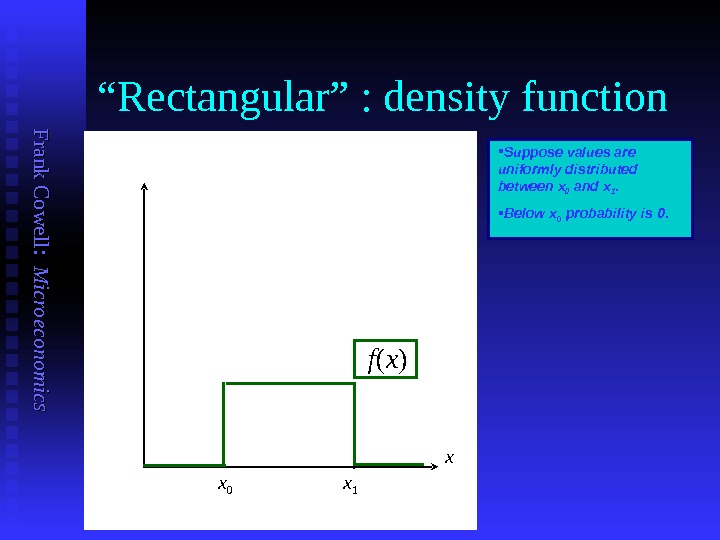
 F ran k C o w ell: M icro eco n o m ics “ Rectangular” : density function x Below x 0 probability is 0. x 1 x 0 Suppose values are uniformly distributed between x 0 and x 1. f ( x )
F ran k C o w ell: M icro eco n o m ics “ Rectangular” : density function x Below x 0 probability is 0. x 1 x 0 Suppose values are uniformly distributed between x 0 and x 1. f ( x )
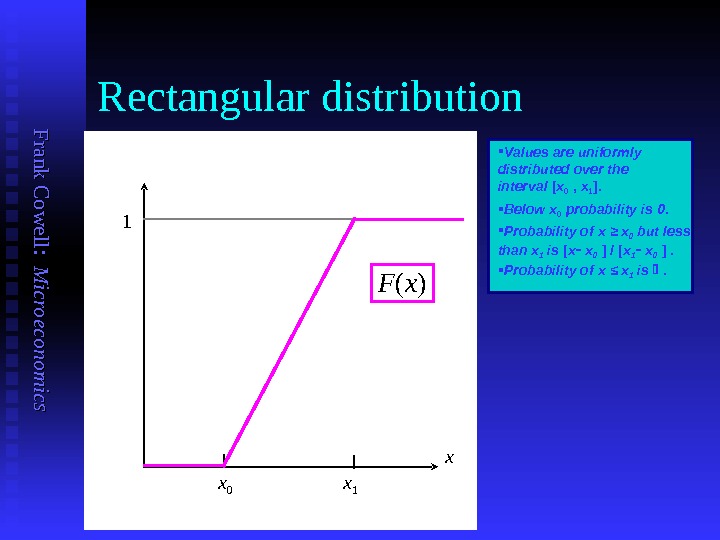
 F ran k C o w ell: M icro eco n o m ics Rectangular distribution x Below x 0 probability is 0. Probability of x ≥ x 0 but less than x 1 is [ x x 0 ] / [ x 1 x 0 ] . x 1 x 01 Probability of x ≤ x 1 is . Values are uniformly distributed over the interval [ x 0 , x 1 ]. F ( x )
F ran k C o w ell: M icro eco n o m ics Rectangular distribution x Below x 0 probability is 0. Probability of x ≥ x 0 but less than x 1 is [ x x 0 ] / [ x 1 x 0 ] . x 1 x 01 Probability of x ≤ x 1 is . Values are uniformly distributed over the interval [ x 0 , x 1 ]. F ( x )
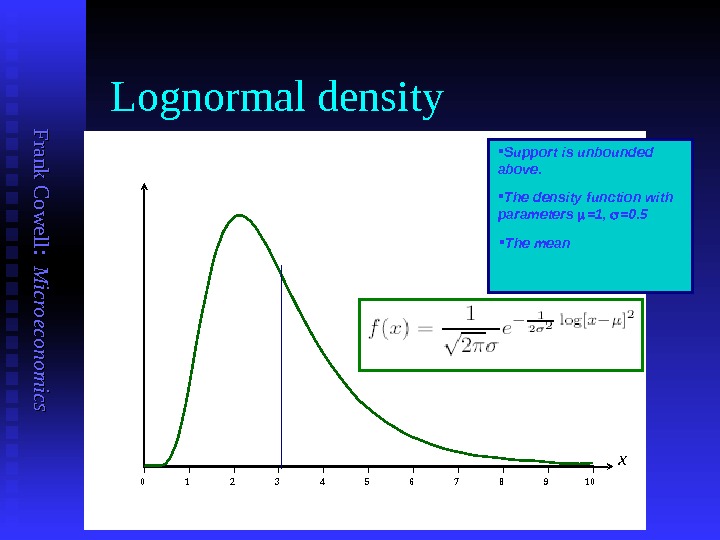
 F ran k C o w ell: M icro eco n o m ics Lognormal density x 0 1 2 3 4 5 6 7 8 9 10 Support is unbounded above. The density function with parameters =1, =0. 5 The mean
F ran k C o w ell: M icro eco n o m ics Lognormal density x 0 1 2 3 4 5 6 7 8 9 10 Support is unbounded above. The density function with parameters =1, =0. 5 The mean
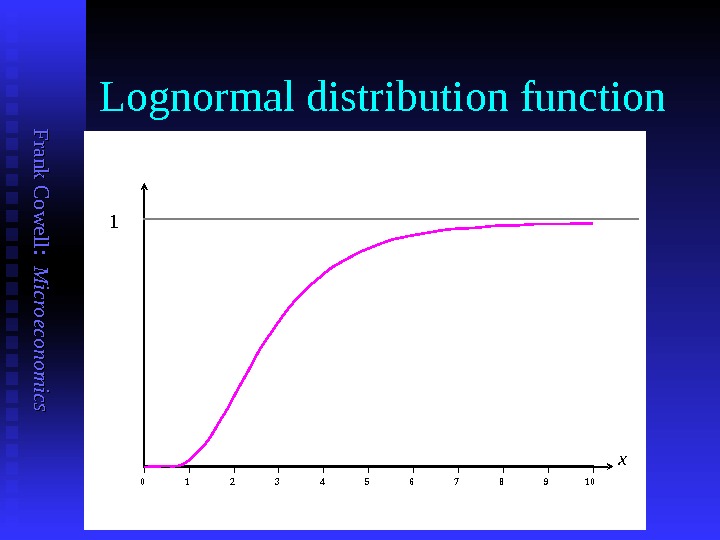
 F ran k C o w ell: M icro eco n o m ics Lognormal distribution function x
F ran k C o w ell: M icro eco n o m ics Lognormal distribution function x
 F ran k C o w ell: M icro eco n o m ics Overview. . . Probability Risk comparisons Special Cases Lotteries. Risk Shape of the u-function and attitude to risk
F ran k C o w ell: M icro eco n o m ics Overview. . . Probability Risk comparisons Special Cases Lotteries. Risk Shape of the u-function and attitude to risk
 F ran k C o w ell: M icro eco n o m ics Risk aversion and the function u With a probability model it makes sense to discuss risk attitudes in terms of gambles Can do this in terms of properties of “felicity” or “cardinal utility” function uu Scale and origin of uu are irrelevant But the curvature of uu is important. We can capture this in more than one way We will investigate the standard approaches. . . and then introduce two useful definitions
F ran k C o w ell: M icro eco n o m ics Risk aversion and the function u With a probability model it makes sense to discuss risk attitudes in terms of gambles Can do this in terms of properties of “felicity” or “cardinal utility” function uu Scale and origin of uu are irrelevant But the curvature of uu is important. We can capture this in more than one way We will investigate the standard approaches. . . and then introduce two useful definitions
 F ran k C o w ell: M icro eco n o m ics Risk aversion and choice Imagine a simple gamble Two payoffs with known probabilities: xx RED with probability RED. . xx BLUE with probability BLUE. . Expected value EE xx = = RED xx. RED + + BLUE xx. BLUE. . A “fair gamble”: stake money is exactly EE xx . . Would the person accept all fair gambles? Compare EE uu (( xx ) with uu (( EE xx ) ) depends on shape of u
F ran k C o w ell: M icro eco n o m ics Risk aversion and choice Imagine a simple gamble Two payoffs with known probabilities: xx RED with probability RED. . xx BLUE with probability BLUE. . Expected value EE xx = = RED xx. RED + + BLUE xx. BLUE. . A “fair gamble”: stake money is exactly EE xx . . Would the person accept all fair gambles? Compare EE uu (( xx ) with uu (( EE xx ) ) depends on shape of u
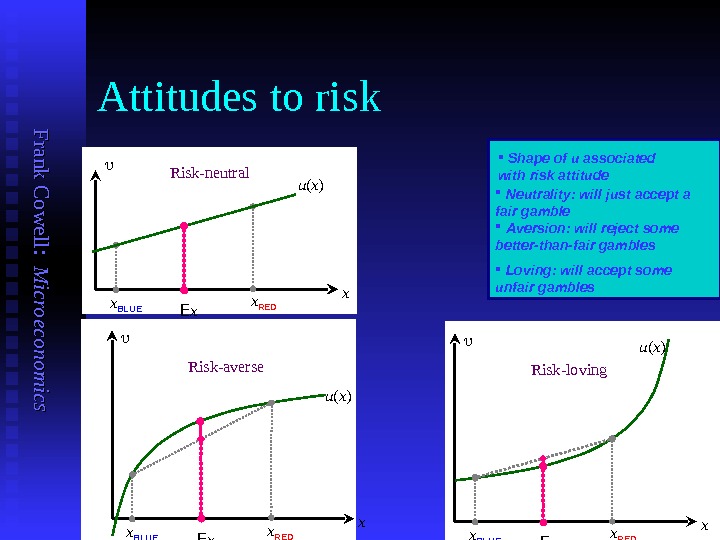
 F ran k C o w ell: M icro eco n o m ics Attitudes to risk u ( x ) x BLUE x x RED E x. Risk-loving u ( x ) x BLUE x x RED E x. Risk-neutral u ( x ) x BLUE x x RED E x Risk-averse Shape of u associated with risk attitude Neutrality: will just accept a fair gamble Aversion: will reject some better-than-fair gambles Loving: will accept some unfair gambles
F ran k C o w ell: M icro eco n o m ics Attitudes to risk u ( x ) x BLUE x x RED E x. Risk-loving u ( x ) x BLUE x x RED E x. Risk-neutral u ( x ) x BLUE x x RED E x Risk-averse Shape of u associated with risk attitude Neutrality: will just accept a fair gamble Aversion: will reject some better-than-fair gambles Loving: will accept some unfair gambles
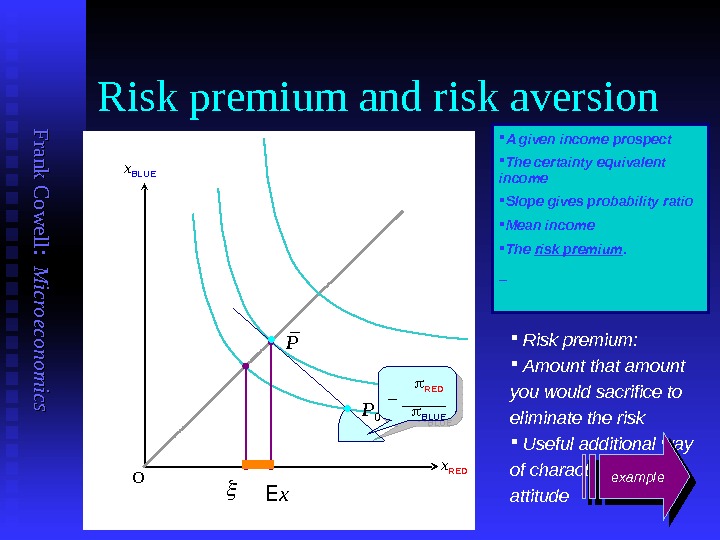
 F ran k C o w ell: M icro eco n o m ics Risk premium and risk aversion x BLUE x RED O RED – _____ BLUE The certainty equivalent income A given income prospect Slope gives probability ratio E x Mean income The risk premium. P 0 P Risk premium: Amount that amount you would sacrifice to eliminate the risk Useful additional way of characterising risk attitude – _ example
F ran k C o w ell: M icro eco n o m ics Risk premium and risk aversion x BLUE x RED O RED – _____ BLUE The certainty equivalent income A given income prospect Slope gives probability ratio E x Mean income The risk premium. P 0 P Risk premium: Amount that amount you would sacrifice to eliminate the risk Useful additional way of characterising risk attitude – _ example
 F ran k C o w ell: M icro eco n o m ics An example. . . Two-state model Subjective probabilities (0. 25, 0. 75) Single-commodity payoff in each case
F ran k C o w ell: M icro eco n o m ics An example. . . Two-state model Subjective probabilities (0. 25, 0. 75) Single-commodity payoff in each case
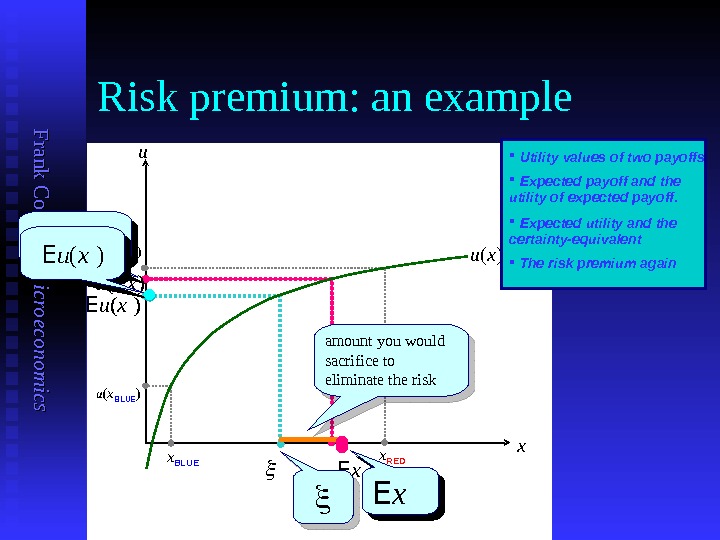
 F ran k C o w ell: M icro eco n o m ics Risk premium: an example u u ( x ) x BLUE x x REDu ( x BLUE )u ( x RED ) E xu ( E x ) E u ( x ) amount you would sacrifice to eliminate the risku ( E x ) E x Expected payoff and the utility of expected payoff. Expected utility and the certainty-equivalent The risk premium again Utility values of two payoffs E u ( x )
F ran k C o w ell: M icro eco n o m ics Risk premium: an example u u ( x ) x BLUE x x REDu ( x BLUE )u ( x RED ) E xu ( E x ) E u ( x ) amount you would sacrifice to eliminate the risku ( E x ) E x Expected payoff and the utility of expected payoff. Expected utility and the certainty-equivalent The risk premium again Utility values of two payoffs E u ( x )
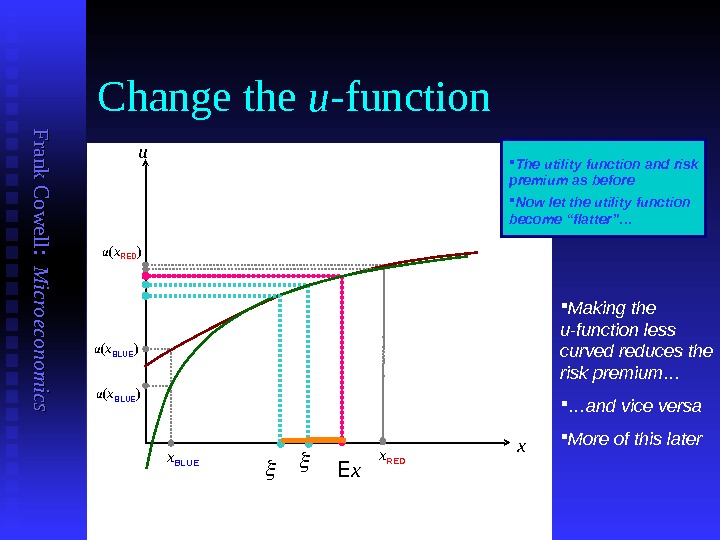
 F ran k C o w ell: M icro eco n o m ics Change the u -function u x BLUE x x REDu ( x BLUE )u ( x RED ) E x The utility function and risk premium as before Now let the utility function become “flatter”… u ( x BLUE ) Making the u-function less curved reduces the risk premium… … and vice versa More of this later
F ran k C o w ell: M icro eco n o m ics Change the u -function u x BLUE x x REDu ( x BLUE )u ( x RED ) E x The utility function and risk premium as before Now let the utility function become “flatter”… u ( x BLUE ) Making the u-function less curved reduces the risk premium… … and vice versa More of this later
 F ran k C o w ell: M icro eco n o m ics An index of risk aversion? Risk aversion associated with shape of uu second derivative or “curvature” But could we summarise it in a simple index or measure? Then we could easily characterise one person as more/less risk averse than another There is more than one way of doing this
F ran k C o w ell: M icro eco n o m ics An index of risk aversion? Risk aversion associated with shape of uu second derivative or “curvature” But could we summarise it in a simple index or measure? Then we could easily characterise one person as more/less risk averse than another There is more than one way of doing this
 F ran k C o w ell: M icro eco n o m ics Absolute risk aversion Definition of absolute risk aversion for scalar payoffs. uu xxxx (( xx )) (( xx ) : = uu xx (( xx ) ) For risk-averse individuals is positive. For risk-neutral individuals is zero. Definition ensures that is independent of the scale and the origin of uu. . Multiply uu by a positive constant… …… add any other constant… remains unchanged.
F ran k C o w ell: M icro eco n o m ics Absolute risk aversion Definition of absolute risk aversion for scalar payoffs. uu xxxx (( xx )) (( xx ) : = uu xx (( xx ) ) For risk-averse individuals is positive. For risk-neutral individuals is zero. Definition ensures that is independent of the scale and the origin of uu. . Multiply uu by a positive constant… …… add any other constant… remains unchanged.
 F ran k C o w ell: M icro eco n o m ics Relative risk aversion Definition of relative risk aversion for scalar payoffs: uu xxxx (( xx )) (( xx ) : = x x uu xx (( xx ) ) Some basic properties of are similar to those of : : positive for risk-averse individuals. zero for risk-neutrality. independent of the scale and the origin of uu Obvious relation with absolute risk aversion : : (( xx ) = xx (( xx ) )
F ran k C o w ell: M icro eco n o m ics Relative risk aversion Definition of relative risk aversion for scalar payoffs: uu xxxx (( xx )) (( xx ) : = x x uu xx (( xx ) ) Some basic properties of are similar to those of : : positive for risk-averse individuals. zero for risk-neutrality. independent of the scale and the origin of uu Obvious relation with absolute risk aversion : : (( xx ) = xx (( xx ) )
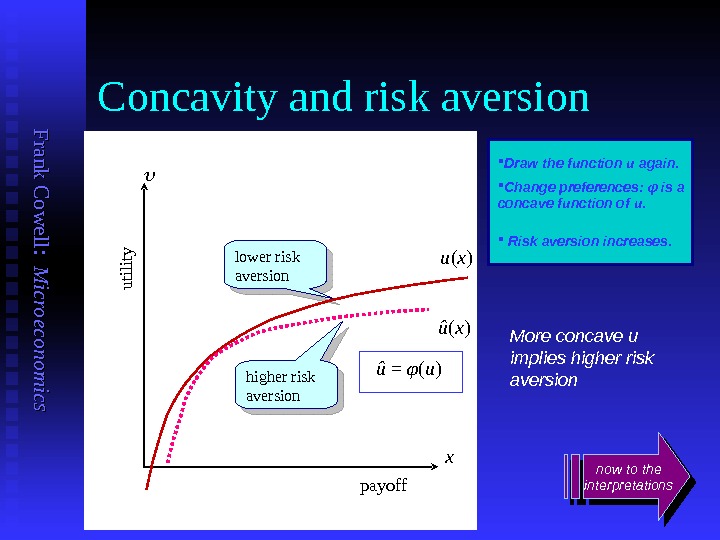
 F ran k C o w ell: M icro eco n o m ics Concavity and risk aversion u ( x ) payoff utility xû ( x ) Draw the function u again. Change preferences: φ is a concave function of u. Risk aversion increases. More concave u implies higher risk aversion now to the interpretationslower risk aversion higher risk aversion û = φ ( u )
F ran k C o w ell: M icro eco n o m ics Concavity and risk aversion u ( x ) payoff utility xû ( x ) Draw the function u again. Change preferences: φ is a concave function of u. Risk aversion increases. More concave u implies higher risk aversion now to the interpretationslower risk aversion higher risk aversion û = φ ( u )
 F ran k C o w ell: M icro eco n o m ics Interpreting and Think of as a measure of the concavity of u. u. Risk premium is approximately ½ (( xx ) var( xx ). ). Likewise think of as the elasticity of marginal u. u. In both interpretations an increase in the “curvature” of uu increases measured risk aversion. Suppose risk preferences change… uu is replaced by ûû , where ûû == φφ (( uu ) and φφ is strictly concave Then both (( xx ) and (( xx ) increase for all xx. . An increase in or or also associated with increased curvature of IC…
F ran k C o w ell: M icro eco n o m ics Interpreting and Think of as a measure of the concavity of u. u. Risk premium is approximately ½ (( xx ) var( xx ). ). Likewise think of as the elasticity of marginal u. u. In both interpretations an increase in the “curvature” of uu increases measured risk aversion. Suppose risk preferences change… uu is replaced by ûû , where ûû == φφ (( uu ) and φφ is strictly concave Then both (( xx ) and (( xx ) increase for all xx. . An increase in or or also associated with increased curvature of IC…
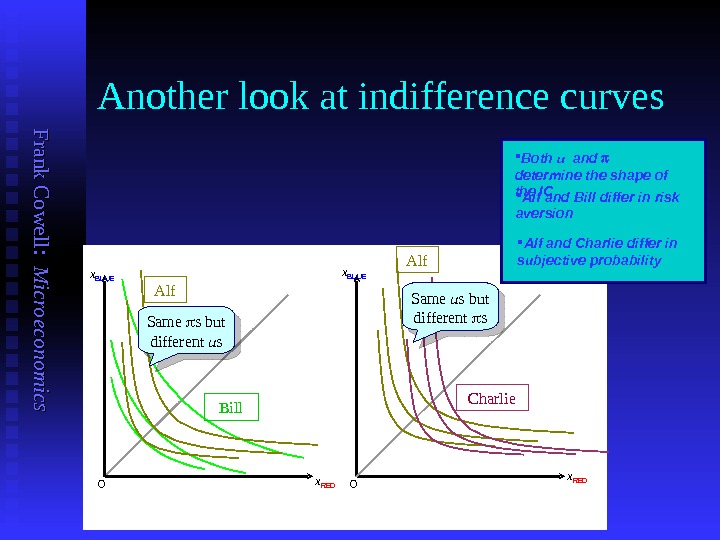
 F ran k C o w ell: M icro eco n o m ics Another look at indifference curves Both u and determine the shape of the IC Alf and Bill differ in risk aversion x BLUE x RED O Alf and Charlie differ in subjective probability Bill. Alf Charlie. Same u s but different s Same s but different u s
F ran k C o w ell: M icro eco n o m ics Another look at indifference curves Both u and determine the shape of the IC Alf and Bill differ in risk aversion x BLUE x RED O Alf and Charlie differ in subjective probability Bill. Alf Charlie. Same u s but different s Same s but different u s
 F ran k C o w ell: M icro eco n o m ics Overview. . . Probability Risk comparisons Special Cases Lotteries. Risk CARA and CRR
F ran k C o w ell: M icro eco n o m ics Overview. . . Probability Risk comparisons Special Cases Lotteries. Risk CARA and CRR
 F ran k C o w ell: M icro eco n o m ics Special utility functions? Sometimes convenient to use special assumptions about risk. Constant ARA Constant RRA By definition (( xx ) = xx (( xx ) ) Differentiate w. r. t. xx : : dd (( xx ) d (( xx )) = = (( xx ) + x x dd x dd xx So one could have, for example: constant ARA and increasing RRA constant RRA and decreasing ARA or, of course, decreasing ARA and increasing RR
F ran k C o w ell: M icro eco n o m ics Special utility functions? Sometimes convenient to use special assumptions about risk. Constant ARA Constant RRA By definition (( xx ) = xx (( xx ) ) Differentiate w. r. t. xx : : dd (( xx ) d (( xx )) = = (( xx ) + x x dd x dd xx So one could have, for example: constant ARA and increasing RRA constant RRA and decreasing ARA or, of course, decreasing ARA and increasing RR
 F ran k C o w ell: M icro eco n o m ics Special case 1: CARA We take a special case of risk preferences Assume that (( xx ) = for all xx Felicity function must take the form 1 1 uu (( xx ) : = e e xx Constant Absolute Risk Aversion This induces a distinctive pattern of indifference curves. . .
F ran k C o w ell: M icro eco n o m ics Special case 1: CARA We take a special case of risk preferences Assume that (( xx ) = for all xx Felicity function must take the form 1 1 uu (( xx ) : = e e xx Constant Absolute Risk Aversion This induces a distinctive pattern of indifference curves. . .
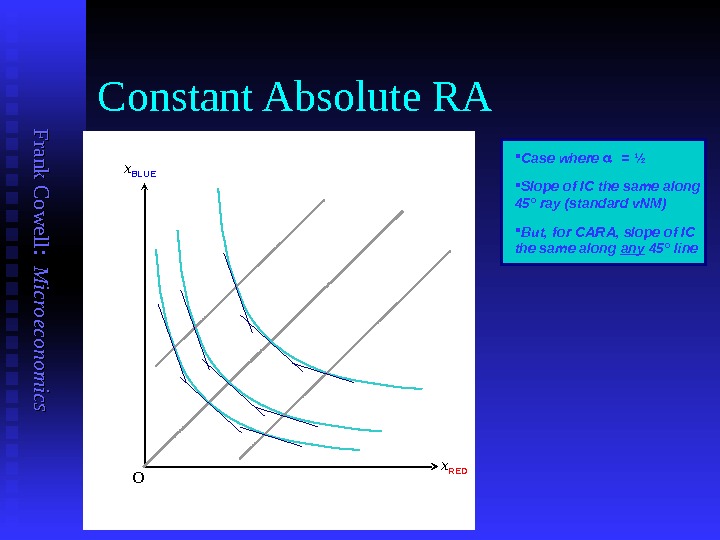
 F ran k C o w ell: M icro eco n o m ics Constant Absolute RA Case where = ½ Slope of IC the same along 45 ° ray (standard v. NM) But, for CARA, slope of IC the same along any 45° line x BLUE x RED O
F ran k C o w ell: M icro eco n o m ics Constant Absolute RA Case where = ½ Slope of IC the same along 45 ° ray (standard v. NM) But, for CARA, slope of IC the same along any 45° line x BLUE x RED O
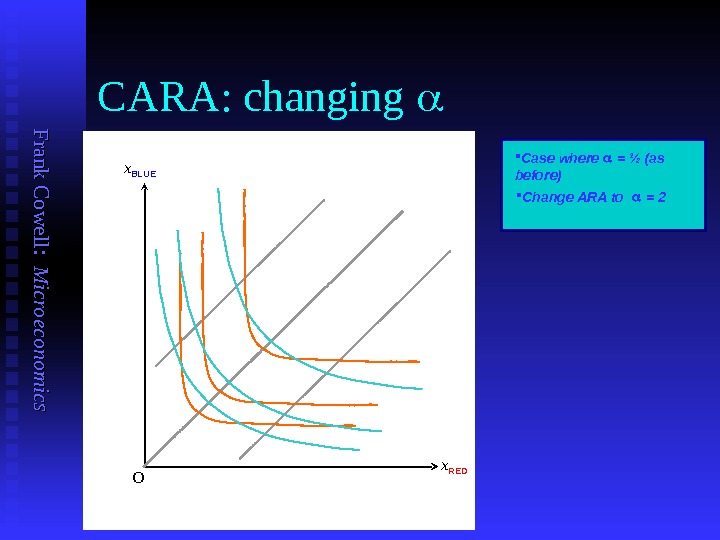
 F ran k C o w ell: M icro eco n o m ics CARA: changing Case where = ½ (as before) Change ARA to = 2 x BLUE x RED O
F ran k C o w ell: M icro eco n o m ics CARA: changing Case where = ½ (as before) Change ARA to = 2 x BLUE x RED O
 F ran k C o w ell: M icro eco n o m ics Special case 2: CRRA Another important special case of risk preferences. Assume that (( xx ) = for all xx. . Felicity function must take the form 1 1 uu (( xx ) : = xx 1 1 1 1 Constant Relative Risk Aversion Again induces a distinctive pattern of indifference curves. . .
F ran k C o w ell: M icro eco n o m ics Special case 2: CRRA Another important special case of risk preferences. Assume that (( xx ) = for all xx. . Felicity function must take the form 1 1 uu (( xx ) : = xx 1 1 1 1 Constant Relative Risk Aversion Again induces a distinctive pattern of indifference curves. . .
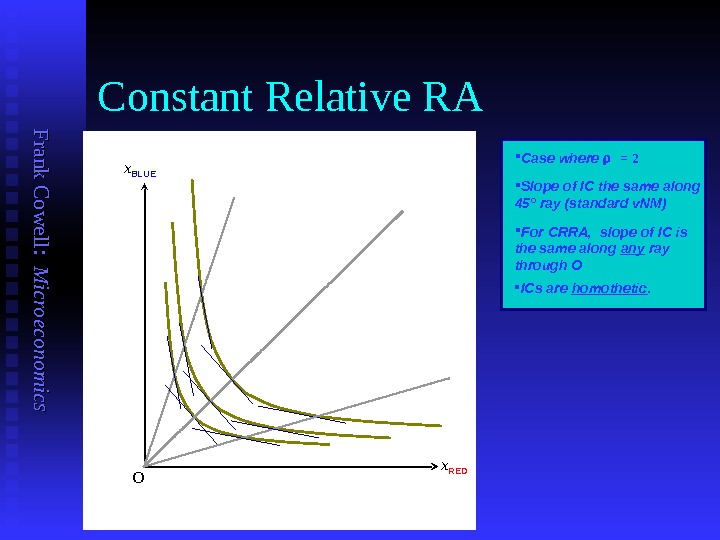
 F ran k C o w ell: M icro eco n o m ics Constant Relative RA Case where = 2 Slope of IC the same along 45 ° ray (standard v. NM) For CRRA, slope of IC is the same along any ray through O ICs are homothetic. x BLUE x RED O
F ran k C o w ell: M icro eco n o m ics Constant Relative RA Case where = 2 Slope of IC the same along 45 ° ray (standard v. NM) For CRRA, slope of IC is the same along any ray through O ICs are homothetic. x BLUE x RED O
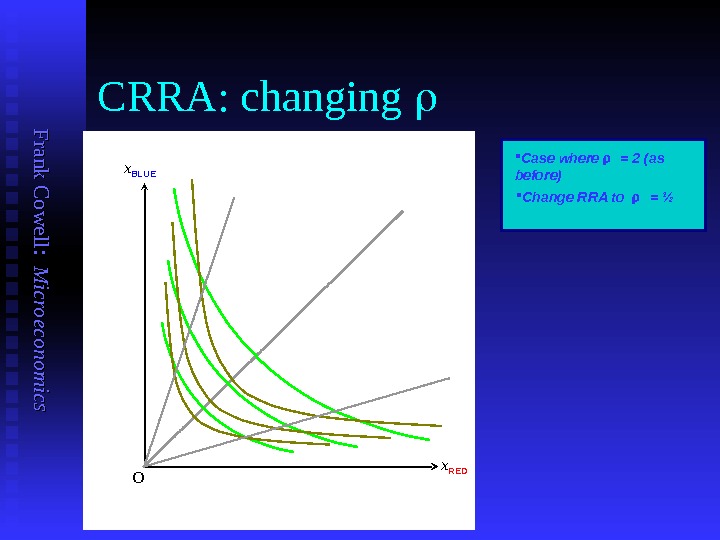
 F ran k C o w ell: M icro eco n o m ics CRRA: changing x BLUE x RED O Case where = 2 (as before) Change RRA to = ½
F ran k C o w ell: M icro eco n o m ics CRRA: changing x BLUE x RED O Case where = 2 (as before) Change RRA to = ½
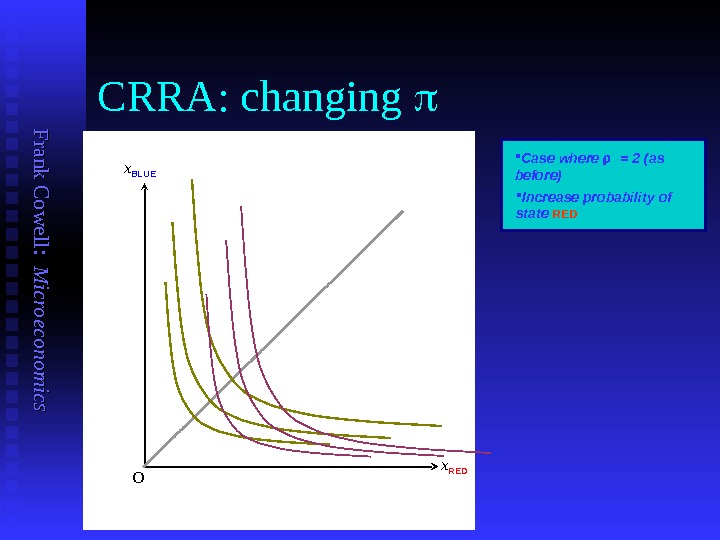
 F ran k C o w ell: M icro eco n o m ics CRRA: changing x BLUE x RED O Case where = 2 (as before) Increase probability of state R
F ran k C o w ell: M icro eco n o m ics CRRA: changing x BLUE x RED O Case where = 2 (as before) Increase probability of state R
 F ran k C o w ell: M icro eco n o m ics Overview. . . Probability Risk comparisons Special Cases Lotteries. Risk Probability distributions as objects of choice
F ran k C o w ell: M icro eco n o m ics Overview. . . Probability Risk comparisons Special Cases Lotteries. Risk Probability distributions as objects of choice
 F ran k C o w ell: M icro eco n o m ics Lotteries Consider lottery as a particular type of uncertain prospect. Take an explicit probability model. Assume a finite number of states-of-the-world Associated with each state are: A known payoff x , , A known probability ≥ 0≥ 0. . The lottery is the probability distribution over the “prizes” x , , =1, 2, . . The probability distribution is just the vector : = ( , , , …, ) ) Of course, + + +…++…+ = 1. What of preferences?
F ran k C o w ell: M icro eco n o m ics Lotteries Consider lottery as a particular type of uncertain prospect. Take an explicit probability model. Assume a finite number of states-of-the-world Associated with each state are: A known payoff x , , A known probability ≥ 0≥ 0. . The lottery is the probability distribution over the “prizes” x , , =1, 2, . . The probability distribution is just the vector : = ( , , , …, ) ) Of course, + + +…++…+ = 1. What of preferences?
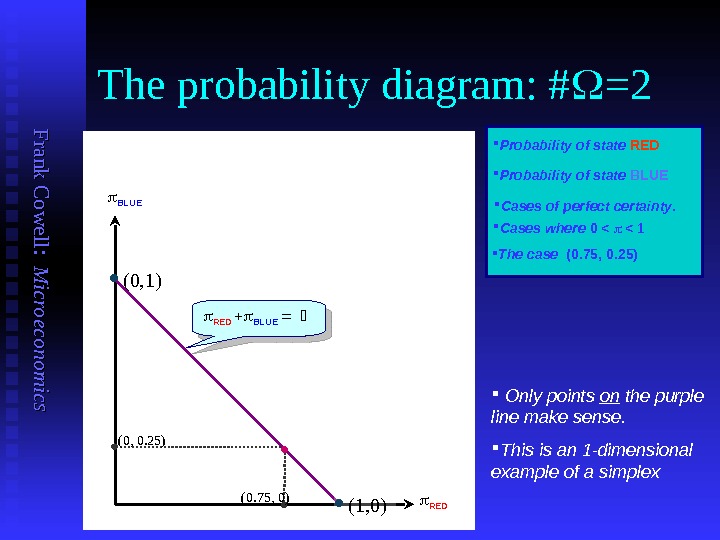
 F ran k C o w ell: M icro eco n o m ics The probability diagram: # =2 BLUE RED (1, 0) (0, 1) Cases where 0 < < 1 Probability of state BLUE Cases of perfect certainty. Probability of state RED BLUE The case (0. 75, 0. 25) • (0, 0. 25) (0. 75, 0) Only points on the purple line make sense. This is an 1 -dimensional example of a simplex
F ran k C o w ell: M icro eco n o m ics The probability diagram: # =2 BLUE RED (1, 0) (0, 1) Cases where 0 < < 1 Probability of state BLUE Cases of perfect certainty. Probability of state RED BLUE The case (0. 75, 0. 25) • (0, 0. 25) (0. 75, 0) Only points on the purple line make sense. This is an 1 -dimensional example of a simplex
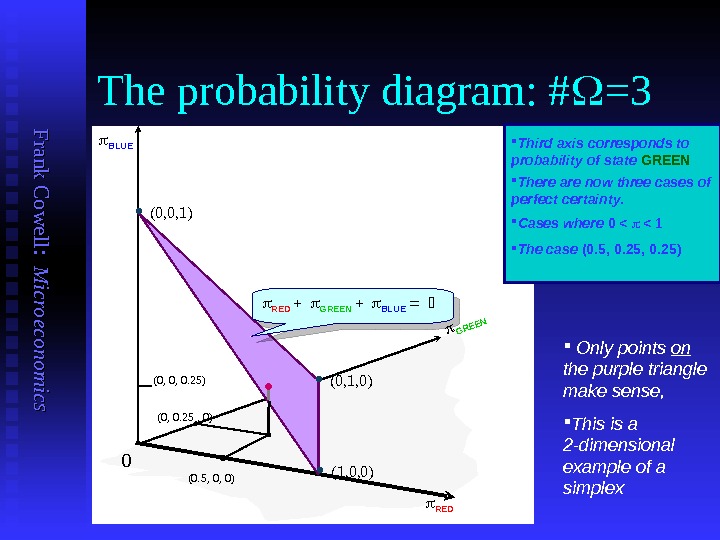
 F ran k C o w ell: M icro eco n o m ics The probability diagram: # =3 0 BLUE RED GREEN Third axis corresponds to probability of state GREEN (1, 0, 0) (0, 0, 1) (0, 1, 0) There are now three cases of perfect certainty. Cases where 0 < < 1 RED GREEN BLUE • (0, 0, 0. 25) (0. 5, 0, 0) (0, 0. 25 , 0) The case (0. 5, 0. 25) Only points on the purple triangle make sense, This is a 2 -dimensional example of a simplex
F ran k C o w ell: M icro eco n o m ics The probability diagram: # =3 0 BLUE RED GREEN Third axis corresponds to probability of state GREEN (1, 0, 0) (0, 0, 1) (0, 1, 0) There are now three cases of perfect certainty. Cases where 0 < < 1 RED GREEN BLUE • (0, 0, 0. 25) (0. 5, 0, 0) (0, 0. 25 , 0) The case (0. 5, 0. 25) Only points on the purple triangle make sense, This is a 2 -dimensional example of a simplex
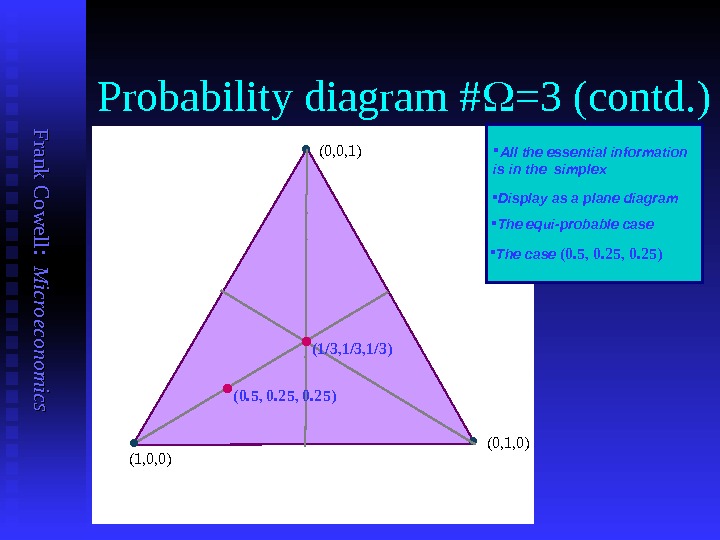
 F ran k C o w ell: M icro eco n o m ics Probability diagram # =3 (contd. ) (1, 0, 0) (0, 0, 1) (0, 1, 0) . • (0. 5, 0. 25) All the essential information is in the simplex Display as a plane diagram The equi-probable case The case (0. 5, 0. 25) • (1/3, 1/3)
F ran k C o w ell: M icro eco n o m ics Probability diagram # =3 (contd. ) (1, 0, 0) (0, 0, 1) (0, 1, 0) . • (0. 5, 0. 25) All the essential information is in the simplex Display as a plane diagram The equi-probable case The case (0. 5, 0. 25) • (1/3, 1/3)
 F ran k C o w ell: M icro eco n o m ics Preferences over lotteries Take the probability distributions as objects of choice Imagine a set of lotteries °° , ‘ , «» , . . . Each lottery has same payoff structure State-of-the-world has payoff x . . . and probability °° or ‘ or » » . . . depending on which lottery We need an alternative axiomatisation for choice amongst lotteries
F ran k C o w ell: M icro eco n o m ics Preferences over lotteries Take the probability distributions as objects of choice Imagine a set of lotteries °° , ‘ , «» , . . . Each lottery has same payoff structure State-of-the-world has payoff x . . . and probability °° or ‘ or » » . . . depending on which lottery We need an alternative axiomatisation for choice amongst lotteries
 F ran k C o w ell: M icro eco n o m ics Axioms on preferences Transitivity over lotteries If If °° < ' and ' < ". . . then °° < ". ". Independence of lotteries If If °° < ' and (0, 1). . then . . . then °° ]] " " < ' ]] "" Continuity over lotteries If If °° ' " then there are numbers and such that °° ]] " " ' ' °° ]] " "
F ran k C o w ell: M icro eco n o m ics Axioms on preferences Transitivity over lotteries If If °° < ' and ' < ". . . then °° < ". ". Independence of lotteries If If °° < ' and (0, 1). . then . . . then °° ]] " " < ' ]] "" Continuity over lotteries If If °° ' " then there are numbers and such that °° ]] " " ' ' °° ]] " "
 F ran k C o w ell: M icro eco n o m ics Basic result Take the axioms transitivity, independence, continuity Imply that preferences must be representable in the form of a von Neumann-Morgenstern utility function: u x or equivalently: where u x So we can also see the EU model as a weighted sum of s. s.
F ran k C o w ell: M icro eco n o m ics Basic result Take the axioms transitivity, independence, continuity Imply that preferences must be representable in the form of a von Neumann-Morgenstern utility function: u x or equivalently: where u x So we can also see the EU model as a weighted sum of s. s.
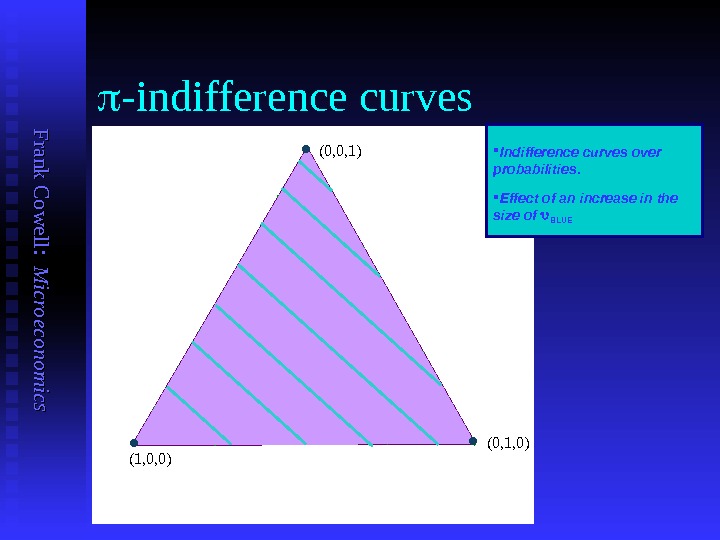
 F ran k C o w ell: M icro eco n o m ics -indifference curves Indifference curves over probabilities. Effect of an increase in the size of BLUE (1, 0, 0) (0, 0, 1) (0, 1, 0) .
F ran k C o w ell: M icro eco n o m ics -indifference curves Indifference curves over probabilities. Effect of an increase in the size of BLUE (1, 0, 0) (0, 0, 1) (0, 1, 0) .
 F ran k C o w ell: M icro eco n o m ics What next? Simple trading model under uncertainty Consumer choice under uncertainty Models of asset holding Models of insurance This is in the presentation Risk Taking
F ran k C o w ell: M icro eco n o m ics What next? Simple trading model under uncertainty Consumer choice under uncertainty Models of asset holding Models of insurance This is in the presentation Risk Taking

