F 301_CH 6 -1 We will deal with

F 301_CH 6 -1 We will deal with 3 different rates: i. Nom = nominal, or stated, or quoted, rate per year. i. Per = periodic rate. effective annual EAR = EFF% =. rate

F 301_CH 6 -2 n i. Nom is stated in contracts. Periods per year (m) must also be given. This is also frequently referred to as an Annual Percentage Rate (APR). n Examples: n 8%; Quarterly n 8%, Daily interest (365 days)

F 301_CH 6 -3 n Periodic rate = i. Per = i. Nom/m, where m is number of compounding periods per year. m = 4 for quarterly, 12 for monthly, and 360 or 365 for daily compounding. n Examples: 8% quarterly: i. Per = 8%/4 = 2%. 8% daily (365): i. Per = 8%/365 = 0. 021918%.

F 301_CH 6 -4 n Effective Annual Rate (EAR = EFF%): Our bank offers a Certificate of Deposit (CD) with a 10% nominal rate, compounded semiannually. What is the true rate of interest that they pay annually (the effective annual rate)? 0 $1 5% 6 mo 12 mo 5%

F 301_CH 6 -5 How do we find EFF% for a nominal rate of 10%, compounded semiannually? ( ) -1 = (1 + 0. 10) - 1. 0 2 i. Nom EFF% = 1 + m m 2 = (1. 05)2 - 1. 0 = 0. 1025 = 10. 25%. Any PV would grow to the same FV at 10. 25% annually or 10% semiannually. In both instances, our money earns 10. 25 percent each year.

F 301_CH 6 -6 For a given rate, more frequent compounding increases returns 12 percent compounded annually EARA = 12%. 12 percent compounded semi-annually EARs = (1 + 0. 12/2)2 - 1 = 12. 36%. 12 percent compounded monthly EARM = (1 + 0. 12/12)12 - 1 12 percent compounded daily = 12. 68%. EARD(365) = (1 + 0. 12/365)365 - 1 = 12. 75%.

F 301_CH 6 -7 What is the FV of $100, if you earn 10 percent compounded semi-annually? When using semi-annual periods we use the periodic rate: 6 5 N INPUTS I/YR 100 PV 0 PMT FV OUTPUT Cpt = 134. 01 When using annual periods we use the EAR: 10. 25 100 0 3 INPUTS N OUTPUT I/YR PV PMT FV Cpt = 134. 01 The nominal rate is never used in calculations!

F 301_CH 6 -8 Can the effective rate ever be equal to the nominal rate? n Yes, but only if annual compounding is used, i. e. , if m = 1. n If m > 1, EFF% will always be greater than the nominal rate.

F 301_CH 6 -9 When is each rate used? The use of the periodic rate and the effective annual rate is determined by the choice of N. If N is the number of years, the EAR is used. If N is the number of periods (shorter than 1 year), the periodic rate is used. The nominal rate is not used in calculations. As shown later, the choice of N will be determined by the number of payments (PMT). i. Nom: Written into contracts, quoted by banks and brokers. Not used in calculations or shown on time lines.

F 301_CH 6 -10 Nominal, Periodic, or Effective Annual Rate? n We never use the nominal rate calculating future or present values. We always use either the effective annual rate or the periodic rate of return. n If PMT is 0, either the periodic rate or the effective rate may be used. l Ex: Find the present value of $100 to be received in 5 years. The nominal rate is 6 percent, compounded monthly. 6/12 Periodic: FV = 100, N = 5*12, I = _______; compute PV= $74. 14 E. A. R. : 6. 1678 FV = 100, N = 5, I = _____; compute PV= $74. 14

F 301_CH 6 -11 n If PMT has a value, N must equal the number of payments. Since N is determined by the number of payments, we must make I (the interest rate) consistent with how we defined N. l Ex: Find the present value of $100 per year for 5 years. The nominal rate is 6 percent, compounded monthly. 6. 1678 PMT = 100, N = 5, I = _____; compute PV = $419. 32 l Ex: Find the present value of $100 per month for 5 years. The nominal rate is 6 percent, compounded monthly. 6/12 PMT = 100, N = 5*12, I = ____; compute PV = $5, 172. 56

F 301_CH 6 -12 A few other points to note. n If the rate is 12% compounded monthly, your EAR is 12. 6825%, this is used if the N is in number of years. n If the rate is quoted at 12% compounded monthly, the periodic rate would be 1% (12%/12). The 1% is used if the N is in number of months. n If the rate is 12% compounded monthly, you cannot divide the 12% by anything besides its number of compounding periods (in this case 12 monthly periods), or you change the interest rate.

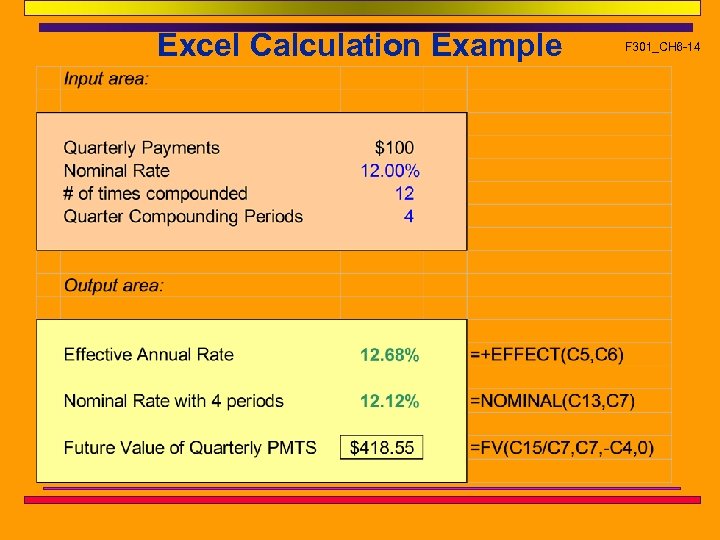
Example F 301_CH 6 -13 n What is the future value of 4 quarterly payments of $100 each, given a nominal rate of 12 percent, compounded monthly. n Note that the quarterly payments and monthly compounding are different, so we have to transform the monthly compounded rate to a quarterly compounded rate. This takes some work. First, find the EAR of the monthly rate: EARM = (1 + 0. 12/12)12 - 1 = 12. 68%. Second, find the nominal rate with quarterly compounding that has an effective annual rate of 12. 68% (1 + Inom/4)4 - 1 = 12. 68%. Inom = 12. 12% Third, compute the future value of the payments N = 4, I = 12. 12/4, PV = 0, PMT = 100, cpt FV = $418. 55 n See the next slide for the Excel Example

Excel Calculation Example F 301_CH 6 -14