d45df70b3a0e7a6c912b3e6c916ee5c8.ppt
- Количество слайдов: 42

Extremum Properties of Orthogonal Quotients Matrices By Achiya Dax Hydrological Service, Jerusalem , Israel e-mail: dax 20@water. gov. il

The Eckart – Young Theorem ( 1936 ) says that the “truncated SVD” matrix Ak = T Uk Dk Vk solves the least norm problem minimize subject to F ( B ) = || A - B || F rank ( B ) £ k ( Also called the Schmidt-Mirsky Theorem. ) 2

Ky Fan’s Maximum Principle ( 1949 ) S a symmetric positive semi-definite n x n matrix Yk the set of orthogonal n x k matrices l 1 + … + lk = max { trace ( Yk. T S Yk ) | YkÎYk } Solution is obtained for the Spectral matrix Vk = [v 1 , v 2 , … , vk]. giving the sum of the largest k eigenvalues.

Outline * The Eckart – Young Theorem and Orthogonal Quotients matrices. * The Orthogonal Quotients Equality. * The Symmetric Quotients Equality and Ky Fan’s extremum principles. * An Extended Extremum Principle.
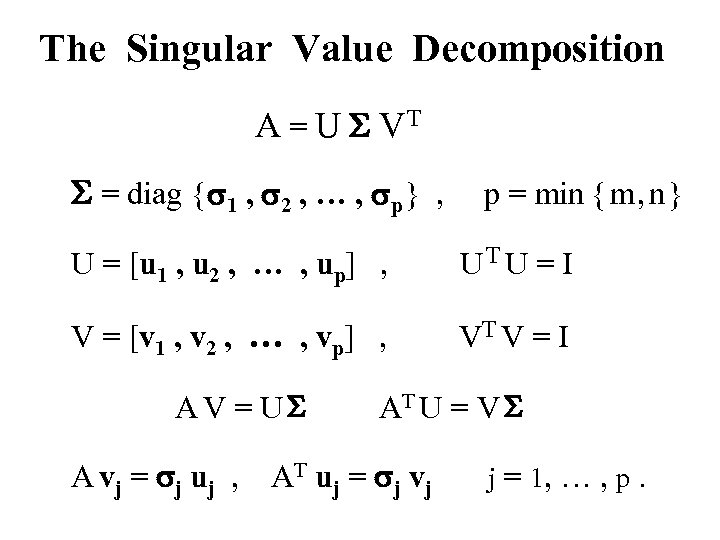
The Singular Value Decomposition A = U S VT S = diag { s 1 , s 2 , … , sp } , p = min { m , n } U = [u 1 , u 2 , … , up] , UT U = I V = [v 1 , v 2 , … , vp] , VT V = I AV = US A vj = sj uj , AT U = V S AT uj = sj vj j = 1, … , p.

Low - Rank Approximations Ak = T Uk Dk Vk Dk = diag { s 1 , s 2 , … , sk } , Uk = [u 1 , u 2 , … , u k] , Vk = [v 1 , v 2 , … , vk] , U k. T U k = I V k. T V k = I

The Eckart – Young Theorem ( 1936 ) says that the “truncated SVD” matrix Ak = Uk Dk Vk. T solves the least norm problem minimize subject to F ( B ) = || A - B || F 2 rank ( B ) £ k ( Also called the Schmidt-Mirsky Theorem. )

Rank - k Matrices B = X k R k Y k. T where Rk is a k x k matrix Xk = [x 1 , x 2 , … , xk] , Yk = [y 1 , y 2 , … , yk] , X k. T X k = I Y k. T Y k = I

The Eckart – Young Problem can be rewritten as minimize F ( B ) = || A - Xk Rk Yk. T || F 2 subject to Xk. T Xk = I and Yk. T Yk = I.

Theorem 1 : Given a pair of orthogonal matrices, Xk and Yk , the related “Orthogonal Quotients Matrix” Xk. T A Yk = ( xi. TAyj ) solves the problem minimize F ( Rk ) = || A - Xk Rk Yk. T || F 2

Notation: Xk - denotes the set of all real m x k orthogonal matrices Xk , Xk = [x 1 , x 2 , … , xk] , X k. T X k = I Yk - denotes the set of all real n x k orthogonal matrices Yk , Yk = [y 1 , y 2 , … , yk] , Yk. T Yk = I

Corollary 1 : The Eckart – Young Problem can be rewritten as minimize F ( Xk, Yk ) = || A - Xk Rk Yk subject to where Rk T || F 2 XkÎXk and YkÎYk , is the “Orthogonal Quotients Matrix” R k = X k. T A Y k .

The Orthogonal Quotients Equality For any pair of orthogonal matrices, XkÎXk and YkÎYk , || A - Xk Rk Yk. T || F 2 = || A || F 2 - || Rk || F 2 where Rk is the orthogonal quotients matrix R k = X k. T A Y k.

Corollary : The Eckart – Young Problem minimize F ( Xk, Yk ) = || A - Xk Rk Yk. T || F 2 subject to XkÎXk and YkÎYk. is equivalent to maximize || Xk. T A Yk || F 2 subject to XkÎXk and YkÎYk , and the SVD matrices Uk giving the optimal value of and Vk solves both problems, s 12 + s 22 + … + sk 2.

Question : Is the related minimum problem minimize || (Xk)T A Yk || F 2 subject to solvable ? XkÎXk and YkÎYk ,

Using the Orthogonal Quotients Equality the last problem takes the form maximize F ( Xk, Yk ) = || A - Xk Rk Yk. T || F 2 subject to XkÎXk and YkÎYk.

Note that the more general problem maximize F ( B ) = || A - B || F 2 subject to rank ( B ) £ k is not solvable.

Returning to symmetric matrices How we extend the Orthogonal Quotients Equality to symmetric matrices ?

The Spectral Decomposition S = ( Sij ) a symmetric positive semi-definite n x n matrix With eigenvalues l 1 ³ l 2 ³. . . ³ ln ³ 0 and eigenvectors v 1 , v 2 , … , vn S vj = lj vj , j = 1, … , n V = [v 1 , v 2 , … , vn] , . SV=VD VT V = V V T = I D = diag { l 1 , l 2 , … , ln } S = V D VT = S lj vj vj. T
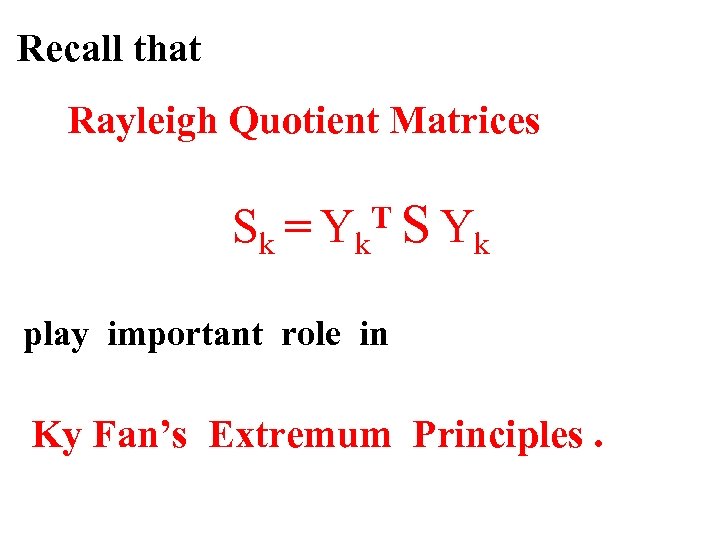
Recall that Rayleigh Quotient Matrices Sk = Yk. T S Yk play important role in Ky Fan’s Extremum Principles.

Ky Fan’s Maximum Principle S a symmetric positive semi-definite n x n matrix Yk the set of orthogonal n x k matrices l 1 + … + lk = max { trace ( Yk. T S Yk ) | YkÎYk } Solution is obtained for the Spectral matrix Vk = [v 1 , v 2 , … , vk]. which is related to the largest k eigenvalues.

Ky Fan’s Minimum Principle S a symmetric n x n matrix. Yk the set of orthogonal n x k matrices. ln - k+1 + … + ln = min { trace ( Yk. T S Yk ) | YkÎYk } Solution is obtained for the Spectral matrix Vk = [vn-k+1 , … , vn] , which is related to the smallest k eigenvalues.

Question : Can we formulate the Symmetric Quotients Equality in terms of trace ( Sk ) = trace ( Yk. T S Yk ) = S yj. T S yj

The Symmetric Quotients Equality S a symmetric n x n matrix YkÎYk an orthogonal n x k matrix S k = Y k. T S Y k the related “Rayleigh quotient matrix” trace ( S - Yk Sk Yk. T ) = trace ( S ) - trace( Sk )

Corollary 1 : Ky Fan’s maximum problem maximize subject to trace (Yk S Yk. T ) Y kÎ Y k , is equivalent to minimize trace ( S - Yk Sk Yk. T ) subject to Y kÎ Y k. The Spectral matrix Vk = [v 1 , v 2 , … , vk] solves both problems, giving the optimal value of l 1 + … + lk.

Recall that : The Eckart – Young Problem minimize F ( Xk, Yk ) = || A - Xk Rk Yk. T || F 2 subject to XkÎXk and YkÎYk. is equivalent to maximize || Xk. T A Yk || F 2 subject to XkÎXk and YkÎYk , and the SVD matrices Uk giving the optimal value of and Vk solves both problems, s 12 + s 22 + … + sk 2.

Corollary 2 : Ky Fan’s minimum problem minimize trace (Yk S Yk. T ) subject to Y kÎ Y k , is equivalent to maximize trace ( S - Yk. T Sk Yk ) subject to Y kÎ Y k. The matrix Vk = [vn-k+1 , … , vn] solves both problems, giving the optimal value of ln-k+1 + … + ln.

Extended Exremum Principles Can we extend these extremums from eigenvalues of symmetric matrices to singular values of rectangular matrices ?

Notation: 1 £ m* £ m , 1 £ n* £ n , Xm* - denotes the set of all real m x m* orthogonal matrices Xm* , Xm* = [x 1 , x 2 , … , xm*] , Xm*T Xm* = I Yn* - denotes the set of all real n x n* orthogonal matrices Yn* , Yn* = [y 1 , y 2 , … , yn*] , Yn* TY * =I

Notations : Given Xm* ÎXm* and Yn* ÎYm* , the m* x n* matrix ( Xm*)TA Yn* = ( xi. TAyj ) is called “Orthogonal Quotients Matrix”.

Notations : The singular values of the Orthogonal Quotients Matrix ( Xm* A Yn* = ( xi. TAyj ) T ) are denoted as h 1 ³ h 2 ³ … ³ hk ³ 0 , where k = min { m*, n* }.

Questions : Which choice of orthogonal matrices Xm* ÎXm* and Yn* ÎYm* , maximizes (or minimizes ) the sum (h 1)p + (h 2)p + … + (hk)p where p > 0 is a given positive constant.

An Extended Maximum Principle : The SVD matrices Um* = [u 1 , u 2 , Vn* = [v 1 , v 2 , … … , um*] and , vn*] solve the problem maximize F ( Xm* , Yn* ) = (h 1)p + (h 2)p + … + (hk)p subject to Xm* ÎXm* and Yn* ÎYn* , for any positive power p > 0 , giving the optimal value of (s 1)p + (s 2)p + … + (sk)p.

An Extended Maximum Principle That is, for any positive power p > 0 , (s 1)p + (s 2)p + … + (sk)p = max{ (h 1)p + (h 2)p +…+ (hk)p | Xm* ÎXm* and Yn* ÎYn*}, and the maximal value is attained for the matrices Um* = [u 1 , u 2 , … , um*] and Vn* = [v 1 , v 2 , … , vn*].

The proof is based on “rectangular” versions of Cauchy Interlace Theorem and Poincare Separation Theorem.

Corollary 1 : When p = 1 the SVD matrices Um* = [u 1 , u 2 , … , um*] and Vn* = [v 1 , v 2 , … solve the “Rectangular Ky Fan problem” maximize F ( Xm* , Yn* ) = h 1 + h 2 + … + hk subject to Xm* ÎXm* and Yn* ÎYn* , giving the optimal value of s 1 + s 2 + … + sk. , vn*]

Corollary 2 : When p = 1 and m* = n* = k the SVD matrices U k = [u 1 , u 2 , … , uk] and Vk = [v 1 , v 2 , … , vk] solve the maximum trace problem maximize F ( Xk , Yk ) = trace ( (Xk)T A Yk ) subject to Xk ÎXk and Yk ÎYk , giving the optimal value of s 1 + s 2 + … + sk. * See also Horn & Johnson, “Topics in Matrix Analysis”, p. 195.

Corollary 3 : When p = 2 the SVD matrices Um* = [u 1 , u 2 , … , um*] and Vn* = [v 1 , v 2 , … , vn*] solve the “rectangular Eckart – Young problem” maximize F ( Xm* , Yn* ) = || (Xm*)T A Yn* || F 2 subject to Xm* ÎXm* and Yn* ÎYn* , giving the optimal value of (s 1)2 + (s 2)2 + … + (sk)2.

An Extended Minimum Principle Question : Can we prove a similar minimum principle ? Answer : Yes, but the solution matrices are more complicated.

An Extended Minimum Principle : Here we consider the problem minimize F( Xm* , Yn* ) = (h 1)p + (h 2)p + … subject to + (hk)p Xm* ÎXm* and Yn* ÎYn* , for any positive power p > 0. The solution matrices are obtained by deleting some columns from the SVD matrices U = [u 1 , u 2 , … , um] and V = [v 1 , v 2 , … , vn].

Summary * The Eckart – Young Theorem and Orthogonal Quotients matrices. * The Orthogonal Quotients Equality. * The Symmetric Quotients Equality and Ky Fan’s extremum principles. * An Extended Extremum Principle.

The END Thank You
d45df70b3a0e7a6c912b3e6c916ee5c8.ppt