Extra dimensions and modified gravity Cédric Deffayet APC

Extra dimensions and modified gravity Cédric Deffayet (APC, CNRS, Paris) 1. Introduction IAGRG-26 2. DGP model Allahabad January 2011 3. The Vainshtein mechanism of « massive gravity » . 4. New models for large distance modifications of gravity (k-Mouflage, Galileon, Kinetic Gravity Braiding …)

1. Introduction Why to modify gravity ? Why extra dimensions ?

Why to modify gravity ? One way to get rid of dark energy ? Changing the dynamics of gravity ? Historical example the success/failure of both approaches: Le Verrier and • The discovery of Neptune • The non discovery of Vulcan… but that of General Relativity Dark matter or dark energy ?

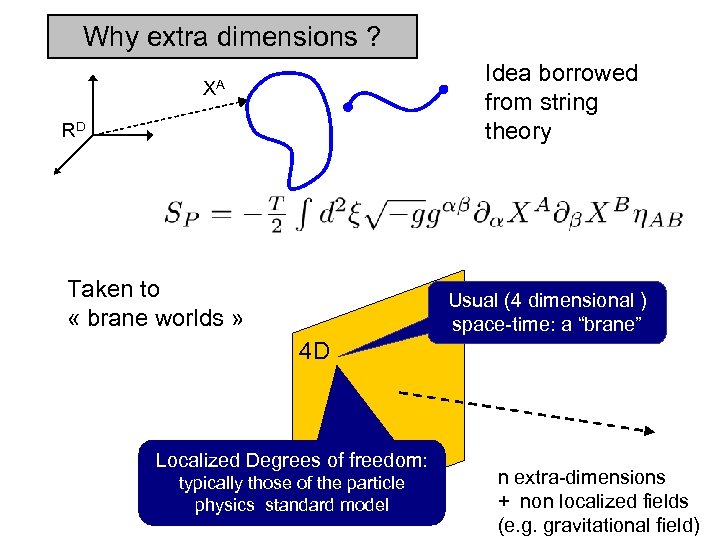Why extra dimensions ? Idea borrowed from string theory XA RD Taken to « brane worlds » Usual (4 dimensional ) space-time: a “brane” 4 D Localized Degrees of freedom: typically those of the particle physics standard model n extra-dimensions + non localized fields (e. g. gravitational field)

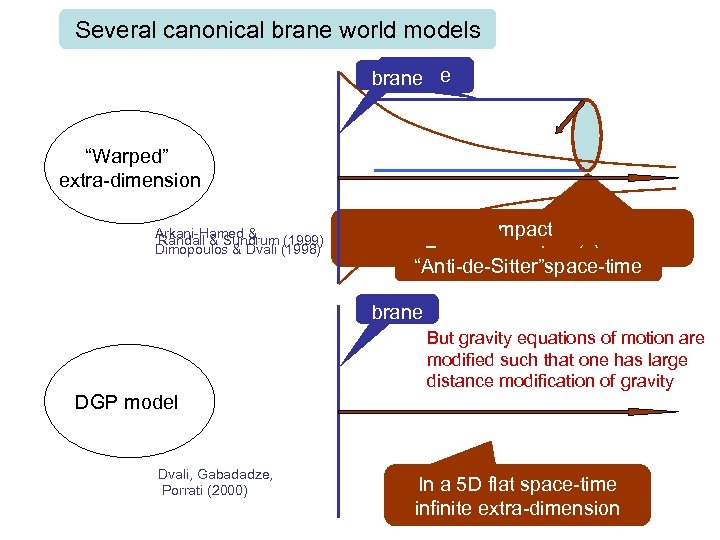Several canonical brane world models brane “Warped” Compact extra-dimensions Arkani-Hamed & Randall & Sundrum (1999) Dimopoulos & Dvali (1998) Compact Extra dimensions(s) “Anti-de-Sitter”space-time brane DGP model Dvali, Gabadadze, Porrati (2000) But gravity equations of motion are modified such that one has large distance modification of gravity In a 5 D flat space-time infinite extra-dimension

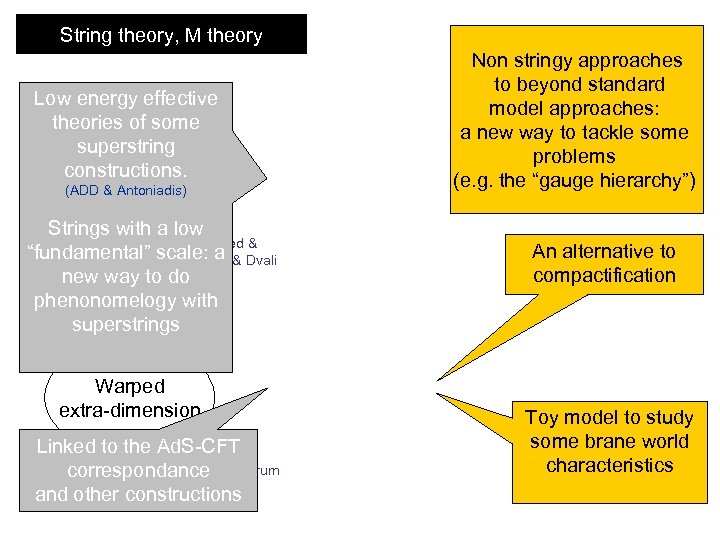String theory, M theory Low energy effective theories of some superstring Compact constructions. (ADD & Antoniadis) extra-dimensions Strings with a low Arkani-Hamed & “fundamental” scale: a Dimopoulos & Dvali new way to do phenonomelogy with superstrings Warped extra-dimension Linked to the Ad. S-CFT Randall & Sundrum correspondance and other constructions Non stringy approaches to beyond standard model approaches: a new way to tackle some problems (e. g. the “gauge hierarchy”) An alternative to compactification Toy model to study some brane world characteristics

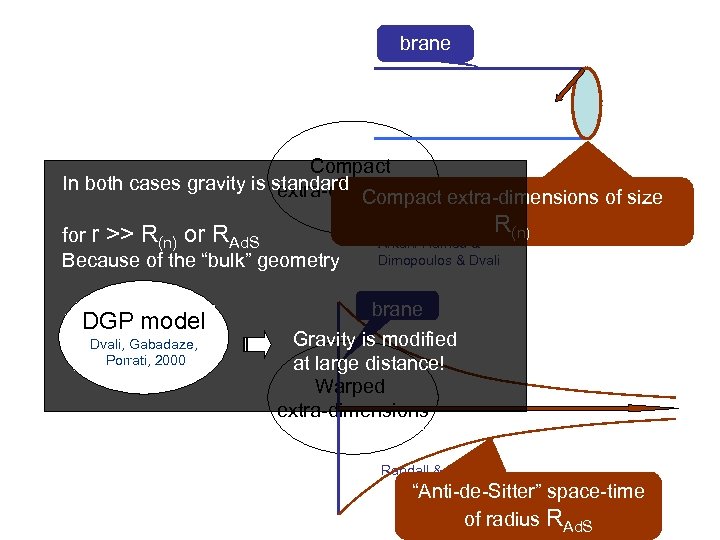brane Compact In both cases gravity is standard extra-dimensions Compact extra-dimensions of size for r >> R(n) or RAd. S Because of the “bulk” geometry DGP model Dvali, Gabadaze, Porrati, 2000 R(n) Arkani-Hamed & Dimopoulos & Dvali brane Gravity is modified at large distance! Warped extra-dimensions Randall & Sundrum “Anti-de-Sitter” space-time of radius RAd. S

In this talk DGP model and ideas following from it …. getting inspired by DGP to build modification of gravity at large distances

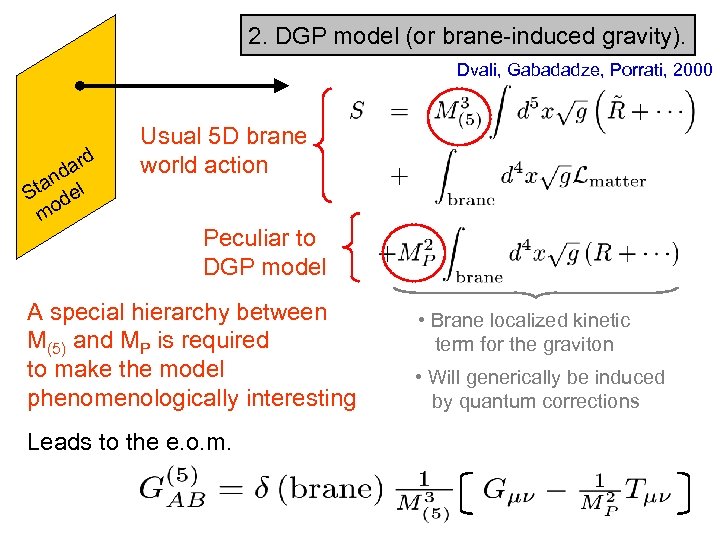2. DGP model (or brane-induced gravity). Dvali, Gabadadze, Porrati, 2000 rd a nd l Sta de mo Usual 5 D brane world action Peculiar to DGP model A special hierarchy between M(5) and MP is required to make the model phenomenologically interesting Leads to the e. o. m. • Brane localized kinetic term for the graviton • Will generically be induced by quantum corrections

DGP model Phenomenological interest A new way to modify gravity at large distance, with a new type of phenomenology … (Important to have such models, if only to disentangle what does and does not depend on the large distance dynamics of gravity in what we know about the Universe) Theoretical interest Consistent (? ) non linear massive gravity …

In the DGP model : • Newtonian potential on the brane behaves as 4 D behavior at small distances 5 D behavior at large distances • The crossover distance between the two regimes is given by This enables to get a “ 4 D looking” theory of gravity out of one which is not, without having to assume a compact (Kaluza. Klein) or “curved” (Randall-Sundrum) bulk. • But the tensorial structure of the graviton propagator is that of a massive graviton (gravity is mediated by a continuum of massive modes) Leads to the van Dam-Veltman-Zakharov discontinuity on Minkowski background!

Homogeneous cosmology of DGP model One obtains the following modified Friedmann equations (C. D. 2001) Energy density of brane localized matter Analogous to standard (4 D) Friedmann equations In the early Universe (small Hubble radii )

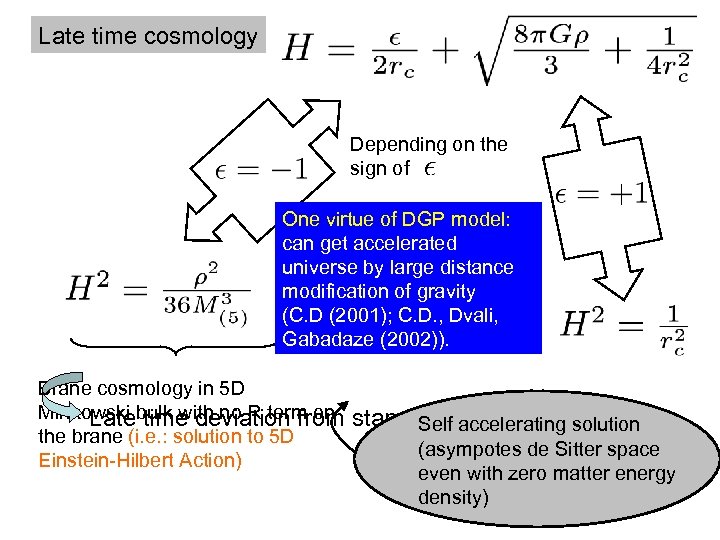Late time cosmology Depending on the sign of One virtue of DGP model: can get accelerated universe by large distance modification of gravity (C. D (2001); C. D. , Dvali, Gabadaze (2002)). Brane cosmology in 5 D Minkowski bulk with no R term on Late time deviation from standard cosmology Self accelerating solution the brane (i. e. : solution to 5 D (asympotes de Sitter space Einstein-Hilbert Action) even with zero matter energy density)

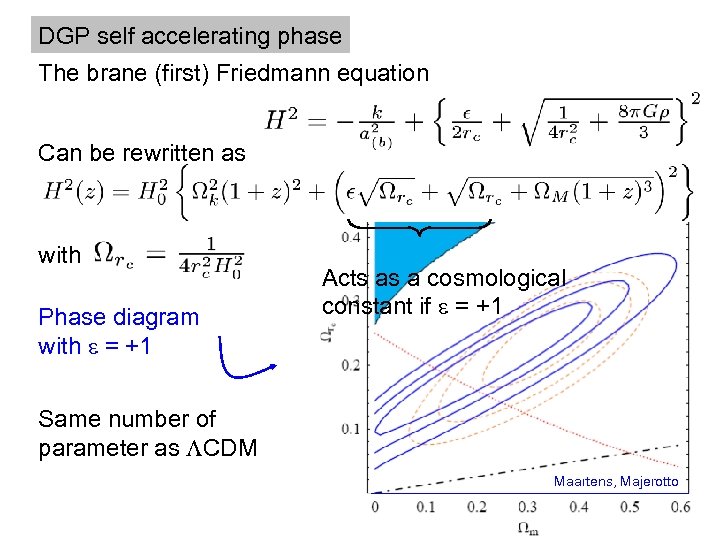DGP self accelerating phase The brane (first) Friedmann equation Can be rewritten as with Phase diagram with = +1 Acts as a cosmological constant if = +1 Same number of parameter as CDM Maartens, Majerotto

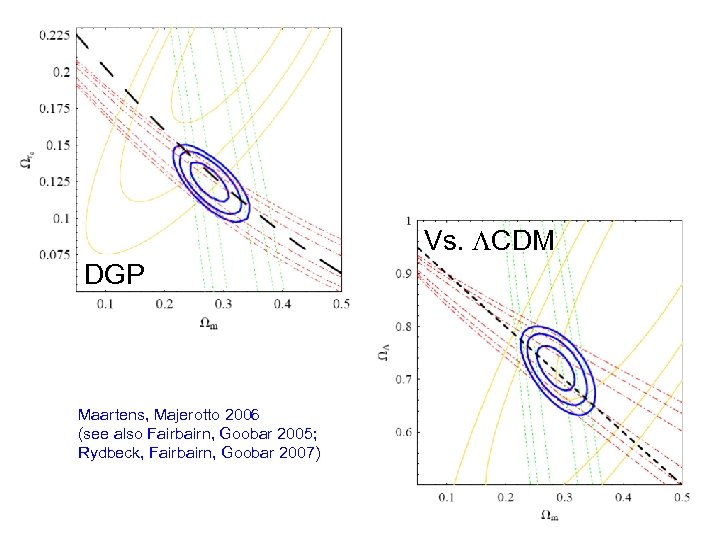Vs. CDM DGP Maartens, Majerotto 2006 (see also Fairbairn, Goobar 2005; Rydbeck, Fairbairn, Goobar 2007)

DGP model and cosmology Interesting (toy) model: first model to show to obtain accelerating Universe from a large distance modification of gravity However a ghost was found in the spectrum of the linearized theory in the self-accelerating phase ! Luty, Porrati, Rattazzi; Nicolis, Rattazzi, Koyama; Gorbunov, Koyama, Sibiryakov; Charmousis, Kaloper, Gregory, Padilla; C. D. , Gabadadze, Iglesias

The meaning of the ghost is not completely clear (because theory also has a low hidden cuttof)… It could possibly be eliminated by putting brane into branes (cascading DGP) De Rahm, Dvali, Hofmann, Khoury, Pujolas, Redi, Tolley, 2008 -2010 It triggered investigations of other models learning from DGP (the rest of this talk) based on particular on the Vainshtein mechanism

3. The Vainshtein mechanism of « massive gravity » 3. 1 Quadratic Pauli-Fierz theory and the v. DVZ discontinuity 3. 2 Non linear Pauli-Fierz theory and the Vainshtein mechanism This mechanism is at the basis of DGP and other more recent models featuring large distance deviations from GR

3. 1 Quadratic massive gravity (and the v. DVZ discontinuity) Pauli-Fierz action: second order action for a massive spin two second order in h ´ g - Only Ghost-free (quadratic) action for a massive spin two Pauli, Fierz (NB: breaks explicitly gauge invariance) The propagators read v. DVZ discontinuity

Coupling the graviton with a conserved energy-momentum tensor The amplitude between two conserved sources T and S is given by For a massless graviton: In Fourier space For a massive graviton:

e. g. amplitude between two non relativistic sources: Instead of Rescaling of Newton constant defined from Cavendish experiment appearing in the action but amplitude between an electromagnetic probe and a non-relativistic source is the same as in the massless case (the only difference between massive and massless case is in the trace part) wrong light bending! (factor ¾)

3. 2 Non linear Pauli-Fierz theory (NB: not a realistic theory) and the Vainshtein mechanism Can be defined by an action of the form Keep all order in h ´ g - At quadratic order in h this reduces to Pauli-Fierz Look at Spherically Symmetric Solutions of this theory Some background metric

+ … Vainshtein 1972 In some kind of non linear PF Wrong light bending! This coefficient equals +1 Introduces a new length scale r in the problem in Schwarzschild solution V below which the perturbation theory diverges! For the sun: bigger than solar system!

So, what is going on at smaller distances? Vainshtein’s answer (1972): There exists an other perturbative expansion at smaller distances, reading: with No warranty that this solution can be matched with the other for large r! Boulware, Deser 1972 • This goes smoothly toward Schwarzschild as m goes to zero • This leads to corrections to Schwarzschild which are non analytic in the Newton constant

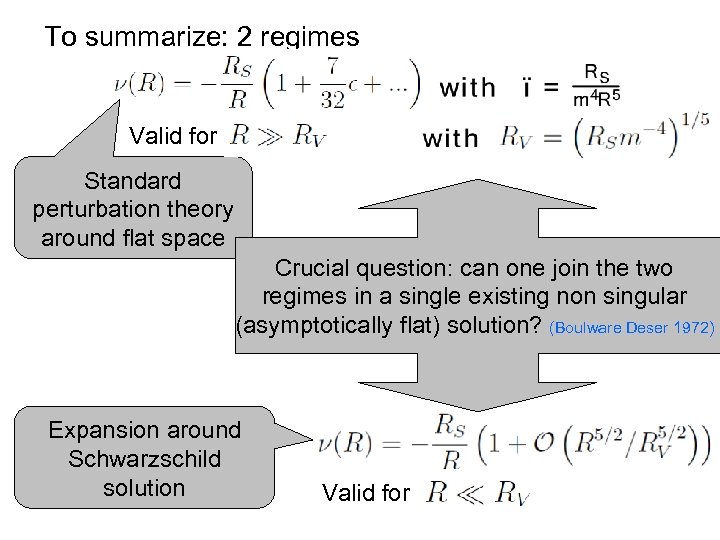To summarize: 2 regimes Valid for R À Rv Standard perturbation theory around flat space Crucial question: can one join the two regimes in a single existing non singular (asymptotically flat) solution? (Boulware Deser 1972) Expansion around Schwarzschild solution Valid for R ¿ Rv

Does it really work ?

This was investigated (by numerical integration) by Damour, Kogan and Papazoglou 2003 No non-singular solution found matching the two behaviours (always singularities appearing at finite radius) and hence failure of the « Vainshtein mechanism » (see also Jun, Kang 1986) We provided a new look on this problem (using in particular the « Goldstone picture » of massive gravity in the « Decoupling limit. » ) In collaboration with E. Babichev and R. Ziour • JHEP 0905: 098, 2009. (ar. Xiv: 0901. 0393) • PRL 103. 201102(ar. Xiv: 0907. 4103) • PRD 82: 104008, 2010 (ar. Xiv: 1007. 4506)

To obtain our solutions, we used the Decoupling Limit, analytic insights (based on resurgence theory extending Borel resummation) …. ……. and numerically… we first… « shooted » Then « relaxed »

With the ansatz (for non linear massive gravity, with two metrics) physical, dynamical, metric Background flat metric

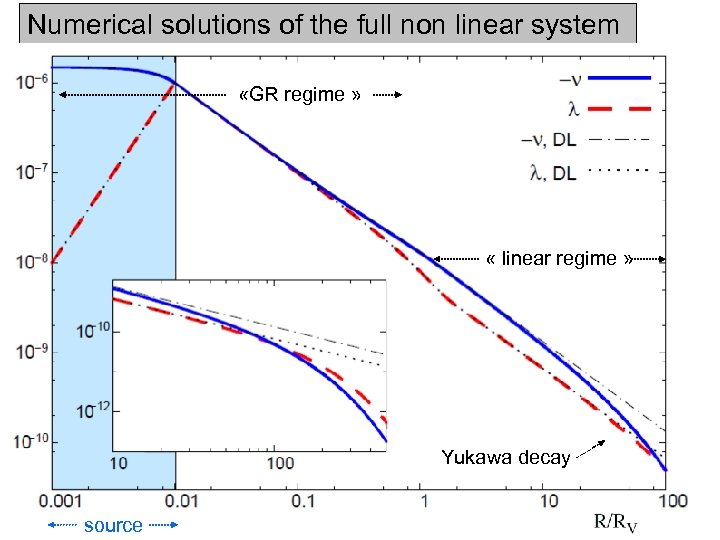Numerical solutions of the full non linear system «GR regime » « linear regime » Yukawa decay source

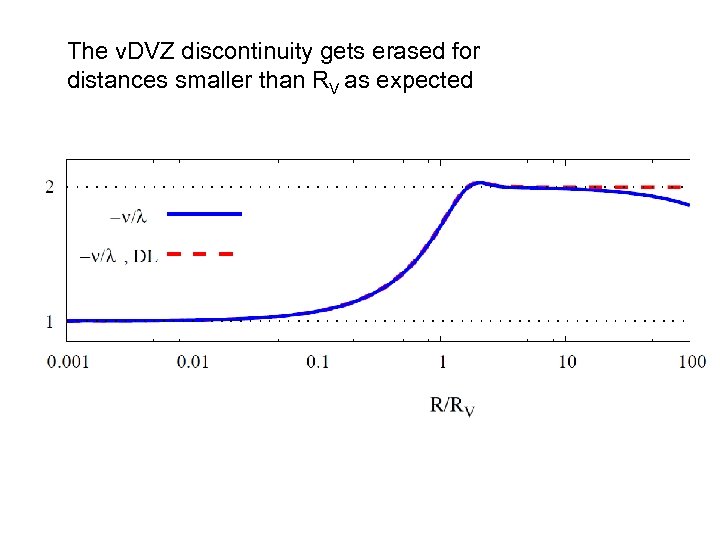The v. DVZ discontinuity gets erased for distances smaller than RV as expected

4. Getting inspired by DGP and massive gravity 4. 1 The decoupling limit 4. 2 k-Mouflage 4. 3 Galileons 4. 4 Kinetic Gravity Braiding

4. 1 The decoupling limit The v. DVZ discontinuity can be understood as being due to the scalar polarization of the (massive) graviton being coupled to the trace of the source energy momentum tensor… While the Vainshtein mecanism can be related to this polarization having strong self interaction C. D. , Gabadadze, Dvali, Vainshtein, 2002 A good (at least qualitatively speaking) description of this is given by the action (obtained by taking a « decoupling limit » )

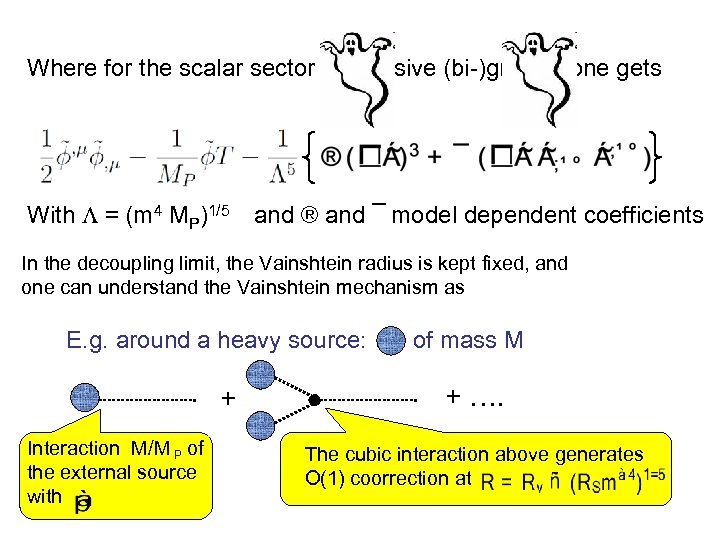Where for the scalar sector of massive (bi-)gravity, one gets With = (m 4 MP)1/5 and ® and ¯ model dependent coefficients In the decoupling limit, the Vainshtein radius is kept fixed, and one can understand the Vainshtein mechanism as E. g. around a heavy source: of mass M + Interaction M/M of P the external source with + …. The cubic interaction above generates O(1) coorrection at

Question: Can one use this do build interesting new models with large distance modifications of gravity ? 4. 2 k-Mouflage

Receipe : take the DL action N. L. completion (and extension)

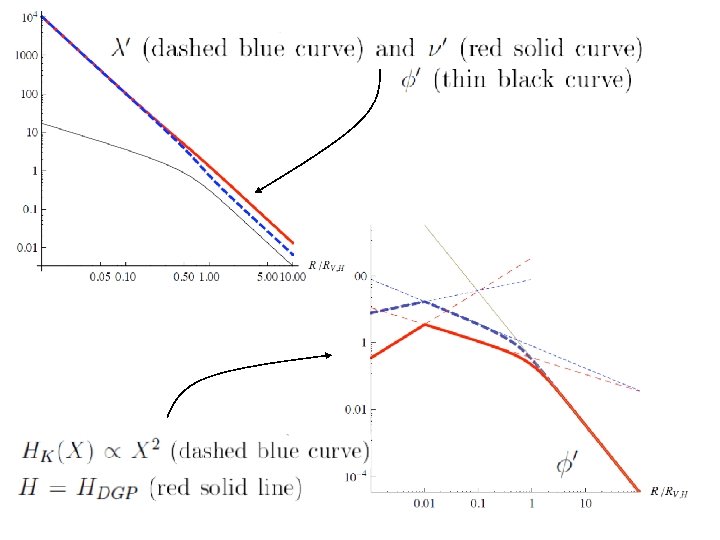
k-Mouflage Nice (toy model) arena to explore to modify gravity in the IR (Nicolis, Rattazzi and Trincherini; Chow, Khoury; Silva, Koyama… for Galileon)

What about cosmology ? 4. 3 Galileon 4. 4 Kinetic Gravity Braiding

Starting from the Decoupling Limit of the DGP model: Scalar sector of the model Energy scale One obtains the following field equations NB: Those are purely second order Luty, Porrati, Rattazzi

The field equations can be obtained from the (5 D) « Hamiltonian » constraint Where one substitutes the Israel junction condition To obtain A last substitution Yield the e. o. m. for

The self accelerating brane « K = constant » and T =0 Corresponds in the DL (using the substitution ) To the solution (and T=0) of the field equations Similar solutions exist in any scalar field theory with field equations which are pure second order Galileon Nicolis, Rattazzi, Trincherini 2009

In 4 D: only 3 non trivial models (With the notations ¼¹ = ¹ ¼ and ¼¹ º = ¹ º ¼ ) Which can be expressed using product of epsilon tensors … e. g.

A lot of interesting aspects an phenomenology still being explored Covariantization C. D. , Deser, Esposito-Farese, Vikman Inflation and non Gaussianity Creminelli, Nicolis, Trincherini, de Felici, Tsujikawa, D’Amico, Musso, Norena, Nesseris, Mota, Sandstad, Zlosnik, Burrage, de Rham, Mota, Tolley, Kobayashi, Silva, Koyama, Yamagushi, Yokoyama … Multi Galileon and p-form Galileon C. D. , Deser, Esposito-Farese, Padilla, Saffin, Zhou, Hinterbichler, Trodden, Wesley …

4. 4 Kinetic Gravity Braiding C. D. , Pujolas, Sawicki, Vikman with The scalar field equations read « Kinetic braiding » Lead to various interesting properties Among which crossing of the phantom divide without ghosts or instabilities

To conclude DGP model • First model to get an accelerating Universe via a large distance modification of gravity • Lack of a good UV completion • Gave new insights on « massive gravity » (use of the Vainshtein mechanism) • Inspired a lot of work Lead to a new family of scalar-tensor models (k-Mouflage, Galileon, Kinetic Gravity Braiding) still to be fully explored (only other competing mechanisms « Chameleon » / « Symmetron » )

Thank you for your invitation and attention