Extending the Reach of Constraint Technology through Reformulation

Extending the Reach of Constraint Technology through Reformulation Alan M. Frisch Artificial Intelligence Group Department of Computer Science University of York CP'2002: 8 Sept 2002 Extending the Reach of Constraint Technology through Reformulation

Combination of Two Papers • Matrix Modelling: Exploiting Common Patterns in Constraint Programming. Pierre Flener, Alan M. Frisch, Brahim Hnich, Zeynep Kiziltan, Ian Miguel, Toby Walsh • Towards CSP Model Reformulation at Multiple Levels of Abstraction. Alan M. Frisch, Brahim Hnich, Ian Miguel, Barbara Smith, Toby Walsh CP'2002: 8 Sept 2002 Extending the Reach of Constraint Technology through Reformulation 2

Formulation Bottleneck • Useful for solving a wide range of important, complex problems including scheduling, allocation, layout. • Modelling a problem as a constraint program requires moderate/great expertise. • Hence constraint technology is used almost exclusively by large enterprises on problems with large payoff. CP'2002: 8 Sept 2002 Extending the Reach of Constraint Technology through Reformulation 3

Reducing the Formulation Bottleneck • Systematise the knowledge of the expert. – Can recognise patterns in problems and match them to patterns of problem formulations. – Can choose among alternatives. • Embed this knowledge in a “compiler” that can reformulate a high-level problem specification into a set of constraints that can be executed efficiently. CP'2002: 8 Sept 2002 Extending the Reach of Constraint Technology through Reformulation 4

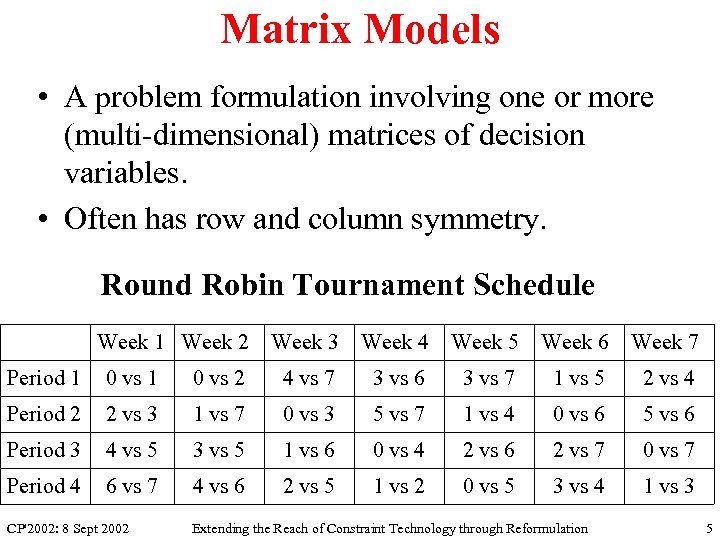Matrix Models • A problem formulation involving one or more (multi-dimensional) matrices of decision variables. • Often has row and column symmetry. Round Robin Tournament Schedule Week 1 Week 2 Week 3 Week 4 Week 5 Week 6 Week 7 Period 1 0 vs 2 4 vs 7 3 vs 6 3 vs 7 1 vs 5 2 vs 4 Period 2 2 vs 3 1 vs 7 0 vs 3 5 vs 7 1 vs 4 0 vs 6 5 vs 6 Period 3 4 vs 5 3 vs 5 1 vs 6 0 vs 4 2 vs 6 2 vs 7 0 vs 7 Period 4 6 vs 7 4 vs 6 2 vs 5 1 vs 2 0 vs 5 3 vs 4 1 vs 3 CP'2002: 8 Sept 2002 Extending the Reach of Constraint Technology through Reformulation 5

Matrix Models are Prevalent • Commonly used to implement sets, subsets, partitions, relations, functions, permutations… • Of 31 problems in CSPlib (www. csplib. org), 27 have natural matrix models, most already published and arguably the most natural models. • Many have row and column symmetries. CP'2002: 8 Sept 2002 Extending the Reach of Constraint Technology through Reformulation 6

Overview I Transforming a CSP instance. II Refining a problem formulation. III Matrix Models – Symmetry breaking & channelling IV Conclusions CP'2002: 8 Sept 2002 Extending the Reach of Constraint Technology through Reformulation 7

Part I: Transforming a CSP Instance CP'2002: 8 Sept 2002 Extending the Reach of Constraint Technology through Reformulation 8

CGRASS • A system that automatically transforms a CSP instance to one that can be solved more efficiently • Transformations: – Introduce implied constraints. – Replace constraints with more powerful ones. – Remove redundant constraints. – Introduce new variables. – Introduce symmetry-breaking constraints. CP'2002: 8 Sept 2002 Extending the Reach of Constraint Technology through Reformulation 9

Performance of CGRASS • Given the naïve model of an instance of the Golomb Ruler Problem, CGRASS can automatically transform it to an efficient CSP formulation (roughly that of Smith, Stergiou & Walsh, 1999). • As Golomb Ruler instances grow in size the time it takes CGRASS to transform the instance grows rapidly. CP'2002: 8 Sept 2002 Extending the Reach of Constraint Technology through Reformulation 10

What Else? • Transform problems, not problem instances • However, transforming the Golomb Ruler problem (formulated as a CSP) requires sophisticated mathematical reasoning. • But transforming an abstract, set-based formulation (sets, subsets, cardinality…) of the Golomb ruler problem is much simpler ! CP'2002: 8 Sept 2002 Extending the Reach of Constraint Technology through Reformulation 11

The Moral of the Story • Transformations must be made at the appropriate level of abstraction. (Some may be best at level of CSP instances. ) • Refinement rules as well as transformation rules are needed. CP'2002: 8 Sept 2002 Extending the Reach of Constraint Technology through Reformulation 12

Part II: Refining a Problem Formulation CP'2002: 8 Sept 2002 Extending the Reach of Constraint Technology through Reformulation

Two Steps to Automatic Refinement Competency: Formulate formal rules for generating alternative refinements. The goal is to generate a set of models that include those generated by experts (perhaps some that are better!). Following on from F [Hnich, forthcoming]. Performance: Generate only the good ones. CP'2002: 8 Sept 2002 Extending the Reach of Constraint Technology through Reformulation 14

SONET Fibre-Optic Communications Problem In a communications network there are client nodes and it is known which pairs of nodes must communicate. Traffic can only be routed between pairs of distinct nodes if they are installed on the same SONET ring. Each node may be installed on multiple rings with each installation requiring a dedicated ADM. There a fixed number of rings available, and each can service a maximum number of ADMs. Configure the network so as to minimize the number of ADMs used. CP'2002: 8 Sept 2002 Extending the Reach of Constraint Technology through Reformulation 15

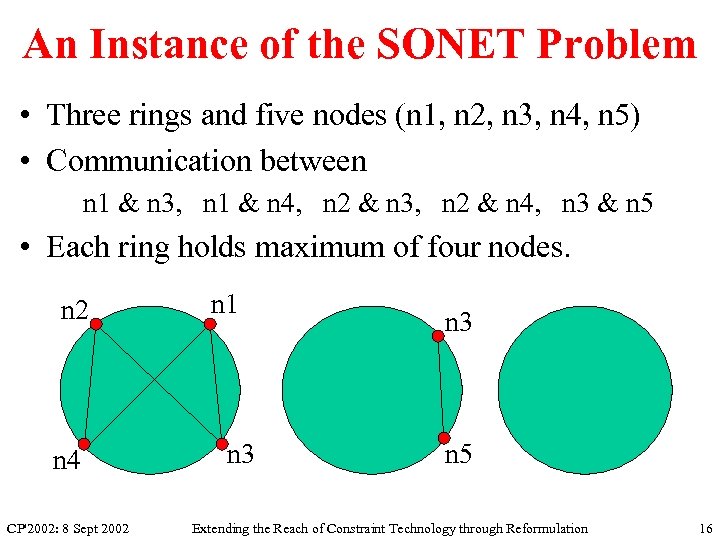An Instance of the SONET Problem • Three rings and five nodes (n 1, n 2, n 3, n 4, n 5) • Communication between n 1 & n 3, n 1 & n 4, n 2 & n 3, n 2 & n 4, n 3 & n 5 • Each ring holds maximum of four nodes. n 2 n 4 CP'2002: 8 Sept 2002 n 1 n 3 n 5 Extending the Reach of Constraint Technology through Reformulation 16

Abstract Mathematical Formulation • • Given: c: ring capacity, R: set of rings, N: set of nodes, D: set of unordered pairs of nodes that communicate Find: rings-nodes: R N Such that: 1) | rings-nodes| is minimised 2) |rings-nodes(r, _)| c, for all r in R 3) rings-nodes(_, n) rings-nodes(_, n ) for all {n, n’} in D CP'2002: 8 Sept 2002 Extending the Reach of Constraint Technology through Reformulation 17

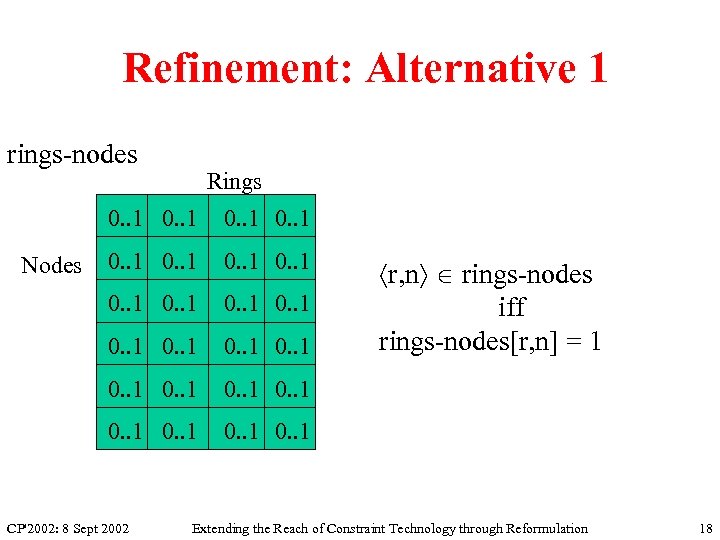Refinement: Alternative 1 rings-nodes Rings 0. . 1 0. . 1 Nodes 0. . 1 CP'2002: 8 Sept 2002 r, n rings-nodes iff rings-nodes[r, n] = 1 Extending the Reach of Constraint Technology through Reformulation 18

Refinement: Alternative 1 1. | rings-nodes| is minimised Minimise(Sr R, n N rings-nodes[r, n] ) 2. |rings-nodes(r, _)| c, for all r R (Sn N rings-nodes[r, n]) c, for all r R 3. (rings-nodes(_, n) rings-nodes(_, n ) for all {n, n } D Sr R (rings-nodes[r, n] rings-nodes[r, n ]) 0 for all {n, n, } D CP'2002: 8 Sept 2002 Extending the Reach of Constraint Technology through Reformulation 19

Refinement Creates Symmetry • R and N are sets. • They are refined to indices of a matrix, which are totally ordered. • Unless some constraint differentiates the elements of a set, our refinement has distinguished indistinguishable objects; it has introduced symmetry. CP'2002: 8 Sept 2002 Extending the Reach of Constraint Technology through Reformulation 20

Refinement Should Break Symmetry • Elements of R are indistinguishable. • n 1 and n 2 are indistinguishable. Other elements of N are distinguished by D. • In rings-nodes, two rows are indistinguishable and all columns are indistinguishable. • Need to break row and column symmetries. CP'2002: 8 Sept 2002 Extending the Reach of Constraint Technology through Reformulation 21

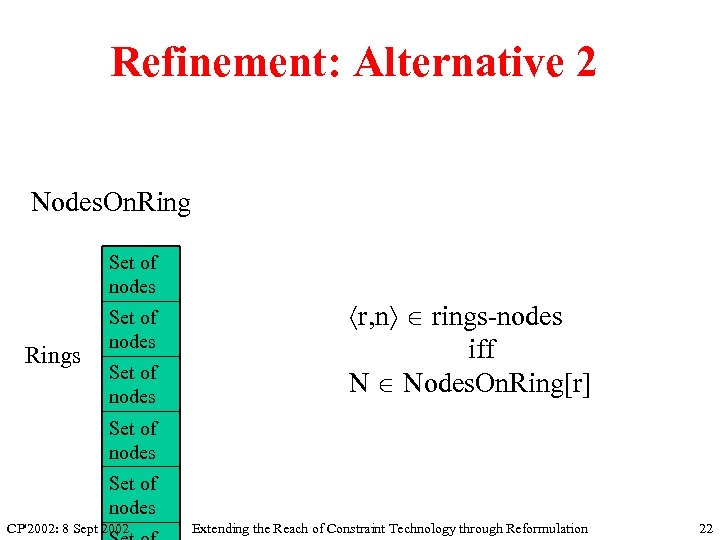Refinement: Alternative 2 Nodes. On. Ring Set of nodes Rings Set of nodes r, n rings-nodes iff N Nodes. On. Ring[r] Set of nodes CP'2002: 8 Sept 2002 Extending the Reach of Constraint Technology through Reformulation 22

Refinement: Alternative 2 • Constraints (1) and (3) can be translated to this representation. • Constraint (2) cannot be expressed directly with this representation. So use 2 D matrix from first alternative and channel. CP'2002: 8 Sept 2002 Extending the Reach of Constraint Technology through Reformulation 23

Summary of SONET Reformulation • Refinement paper presents five different refinements, including that of Smith [ERCIM 2002]. • All produced somewhat systematically by hand. • The first uses a single representation, others channel among two or three representations. • Three complex implied constraints have been added to the abstract formulation and have been refined to each concrete formulation. CP'2002: 8 Sept 2002 Extending the Reach of Constraint Technology through Reformulation 24

Refinement Rules 3. rings-nodes(_, n) rings-nodes(_, n ) for all {n, n } D Sr R (rings-nodes[r, n] rings-nodes[r, n ]) 0 for all {n, n } D CP'2002: 8 Sept 2002 Extending the Reach of Constraint Technology through Reformulation 25

Refinement Rules r(R) = l i 1, …, in . Rm[i 1, …, in] Atomic: r(f f’) = l i 1, …, in . r(f)( i 1, …, in ) r(f’)( i 1, …, in ) Intersect: Cardinality: CP'2002: 8 Sept 2002 r(|f |) = S i 1, …, in X 1 … Xn r(f)( i 1, …, in ) Extending the Reach of Constraint Technology through Reformulation 26

Example of Refinement Refine |A B|, where A, B are relations over X 1 X 2. • r(|A B|) Apply cardinality rule • S i 1, i 2 X 1 X 2 r (A B)( i 1, i 2 ) Apply intersect rule and lambda reduction • S i 1, i 2 X 1 X 2 r (A) ( i 1, i 2 ) • S i 1, i 2 X 1 X 2 r (B) ( i 1, i 2 ) Apply atomic rule and lambda reduction CP'2002: 8 Sept 2002 Am[i 1, i 2] Bm[i 1, i 2] Extending the Reach of Constraint Technology through Reformulation 27

Automatic Generation of Channelling Constraints r, n in rings-nodes iff rings-nodes[r, n] = 1 r, n in rings-nodes iff n Nodes. On. Ring[r] rings-nodes[r, n] = 1 iff n Nodes. On. Ring[r] CP'2002: 8 Sept 2002 Extending the Reach of Constraint Technology through Reformulation 28

Part III: Matrix Models -Symmetry Breaking and Channelling CP'2002: 8 Sept 2002 Extending the Reach of Constraint Technology through Reformulation 29

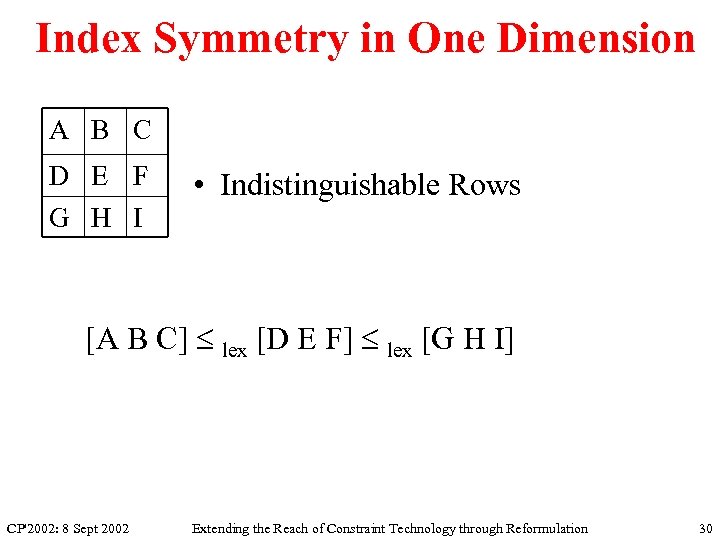Index Symmetry in One Dimension A B C D E F G H I • Indistinguishable Rows [A B C] lex [D E F] lex [G H I] CP'2002: 8 Sept 2002 Extending the Reach of Constraint Technology through Reformulation 30

Index Symmetry in Multiple Dimensions Remove row and column symmetry by adding constraints that rows and cols are lex ordered. • Are these always consistent? (yes) • Does this remove all symmetry? (only sometimes) Breaking Row and Column Symmetries in Matrix Models P. Flener, A. M. Frisch, B. Hnich, Z. Kiziltan, I. Miguel, J. Pearson, T. Walsh CP'2002: 8 Sept 2002 Extending the Reach of Constraint Technology through Reformulation 31

Enforcing Lex Ordering Constraint How efficiently can one maintain GAC on a lex ordering constraint? (linear in size of vectors) Global Constraints for Lexicographic Orderings A. M. Frisch, B. Hnich, Z. Kiziltan, I. Miguel, T. Walsh CP'2002: 8 Sept 2002 Extending the Reach of Constraint Technology through Reformulation 32

Channelling • Many matrix models involve channelling • Matrix paper identifies four types of channelling between matrices and discusses efficient implementation. CP'2002: 8 Sept 2002 Extending the Reach of Constraint Technology through Reformulation 33

Part IV: Conclusion CP'2002: 8 Sept 2002 Extending the Reach of Constraint Technology through Reformulation 34

Hypothesis • It is possible to build a compiler that can take a problem specified in an abstract, high-level language and refine and transform it into a constraint program that can be efficiently executed. CP'2002: 8 Sept 2002 Extending the Reach of Constraint Technology through Reformulation 35

Evidence in Support of Hypothesis • CGRASS can take a CSP instance and perform certain simple transformations to make it easier to solve. • Our formal rules for refining an abstractly-specified problem into an executable specification. • Hnich’s compiler refines function variables. • The executable specifications that are generated often contain matrices of decision variables. We are developing new technology for solving such matrix models (symmetry breaking, channelling and other patterns). CP'2002: 8 Sept 2002 Extending the Reach of Constraint Technology through Reformulation 36

Hypotheses • Without reasoning at a high level of abstraction, automatically transforming a constraint program to an efficient one is unreasonably difficult. CP'2002: 8 Sept 2002 Extending the Reach of Constraint Technology through Reformulation 37

Evidence in Support of Hypotheses We have observed that the complexity of a transformation varies greatly with the level of abstraction of a problem specification. CP'2002: 8 Sept 2002 Extending the Reach of Constraint Technology through Reformulation 38

Major Open Questions • Can complex transformations that increase efficiency be automated? • Can the choice among alternative refinements be automated? • If we succeed in building such a compiler would the reach of constraint programming be extended? CP'2002: 8 Sept 2002 Extending the Reach of Constraint Technology through Reformulation 39

The End CP'2002: 8 Sept 2002 Extending the Reach of Constraint Technology through Reformulation 40

Exploiting Common Patterns • Published in journals with analyses of properties. • Catalogued in textbooks with guidance on selection. • Implemented in program libraries. • Supported by high-level languages. • Exploited by intelligent compilers. This would bring constraint technology to BSc’s. CP'2002: 8 Sept 2002 Extending the Reach of Constraint Technology through Reformulation 41

Example of Refinement Refine |A B|, where A, B are relations over X 1 X 2. • r( | A B | ) S i 1, i 2 e X 1 X 2 r(A B)( i 1, i 2 ) • S i 1, i 2 e X 1 X 2 • l i 1, i 2. (r(A)( i 1, i 2 ) r(B)( i 1, i 2 )) ( i 1, i 2 ) S i 1, i 2 e X 1 X 2 r(A) ( i 1, i 2 ) r(B) ( i 1, i 2 ) • S i 1, i 2 e X 1 X 2 l i 1, i 2. (Am[i 1, i 2]) ( i 1, i 2 ) • l i 1, i 2. (Bm[i 1, i 2]) ( i 1, i 2 ) • S i 1, i 2 e X 1 X 2 CP'2002: 8 Sept 2002 Am[i 1, i 2] Bm[i 1, i 2] Extending the Reach of Constraint Technology through Reformulation 42