Expression-invariant Face Recognition using Geodesic Distance Isometries Kerry

Expression-invariant Face Recognition using Geodesic Distance Isometries Kerry Widder A Review of ‘Robust expression-invariant face recognition from partially missing data’ and other works by A. Bronstein, M. Bronstein and R. Kimmel © 2006 by Kerry R. Widder

Outline • Problem statement • Earlier work (Canonical Form) – – Model Novel idea Implementation Issues • Recent work (Partial Embedding) – – – © 2006 by Kerry R. Widder Motivation New idea Implementation Issues Results Future work 2

Problem Statement Goal: Expression-invariant face recognition using range data images. © 2006 by Kerry R. Widder 3

Earlier Work – “Canonical Forms” (CF) ØModel • Model the face as a Riemannian manifold, S • Use minimal Geodesic distances between points on the face as a representation of the manifold – Intuition: skin on a face moves with expression, but the geodesic distances between points on the face remain almost constant, thus changes in expression are isometric transformations. – Geodesic distances between points show the intrinsic geometry of the face (i. e. , the identity of the face) – Euclidean distances between points show the extrinsic geometry of the face (i. e. , the expression of the face) – Experimental evidence: study done on one subject - data shows geodesic distances are isometric across expressions (is one subject sufficient to make the claim? ? ? ) © 2006 by Kerry R. Widder 4

Earlier Work – “Canonical Forms” (CF) ØNovel idea – Isometric Embedding • Need a distance function for comparison purposes – want d(S, f(S)) = 0 for all functions f which are isometries of S. • Direct use of Geodesic distances has issues due to data being a sampled version of S: – Sample locations may be different between S & f(S) – Number of samples may be different between S & f(S) – Order of samples may be different between S & f(S) • Solution: Represent S as a subset of Rm with the intrinsic geometry approximately preserved – ‘isometric embedding’ – The image produced is called a Canonical Form (CF) © 2006 by Kerry R. Widder 5

Earlier Work – “Canonical Forms” (CF) ØImplementation • • Compute the Geodesic distances using the Fast Marching Method (FMM) – requires O(N 2) or greater to compute. Error criteria: Raw Stress (won’t be exact, resulting in embedding error) – Equation: – Minimize using Multidimensional Scaling (MDS) - O(N 2) to compute • • Perform alignment of the CF image Matching – compare probe CF image with gallery CF images – Higher order moments © 2006 by Kerry R. Widder 6

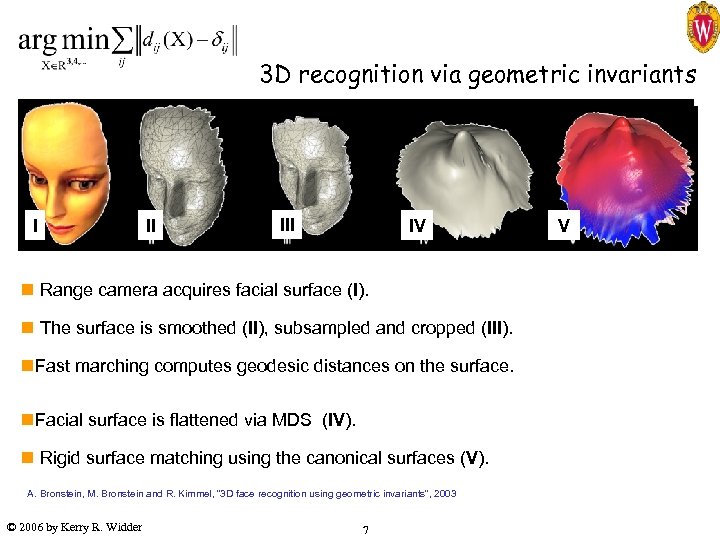3 D recognition via geometric invariants I II IV n Range camera acquires facial surface (I). n The surface is smoothed (II), subsampled and cropped (III). n. Fast marching computes geodesic distances on the surface. n. Facial surface is flattened via MDS (IV). n Rigid surface matching using the canonical surfaces (V). A. Bronstein, M. Bronstein and R. Kimmel, “ 3 D face recognition using geometric invariants“, 2003 © 2006 by Kerry R. Widder 7 V

Earlier Work – “Canonical Forms” (CF) ØIssues • Strength – can pre-compute the signatures • Limitations – – Sensitivity to the definition of the boundaries. No partial matching (including occlusions). Computational complexity O(N 2) requires ≥ 2500 samples for face recognition © 2006 by Kerry R. Widder 8

Recent Work – “Partial Embedding” (PE) ØMotivation • Reduce the error/distortion due to the embedding of a face into the canonical form • Expand the domain of faces that can be handled to include: – Partial faces. – Faces with occlusions. © 2006 by Kerry R. Widder 9

Recent Work – “Partial Embedding” (PE) ØNew Idea • Embed the probe face directly into the target face from the gallery – If the two faces are isometric, the error will be zero. – If the two faces are not isometric, the error will give a measure of their similarity. • Definition: Partial Embedding (PE) – A mapping, φ, of probe face manifold Q onto gallery target face manifold S. © 2006 by Kerry R. Widder 10

Recent Work – “Partial Embedding” (PE) ØImplementation • • Computation of the PE uses a new procedure called ‘Generalized Multidimensional Scaling (GMDS) Error criteria – generalized stress: – – Where ui, i=1, …, M denote the vectors of parametric coordinates of si, and W = (wij) is a symmetric matrix of non-negative weights. – The weights are set to 0 or 1 – if the whole surface is being matched, all are set to 1; if only part of the surface is being matched, the appropriate weights are set to 0. – Minimization of the error is done iteratively • Distance function – – Allows partial matching of faces – Issues with points on the boundary of an occlusion © 2006 by Kerry R. Widder 11

GMDS Bronstein Kimmel 2006 © 2006 by Kerry R. Widder 12

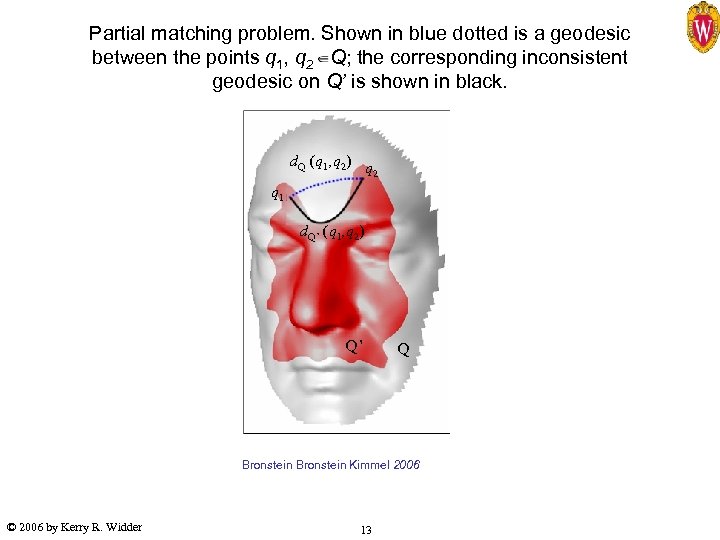Partial matching problem. Shown in blue dotted is a geodesic between the points q 1, q 2 Q; the corresponding inconsistent geodesic on Q’ is shown in black. d. Q (q 1, q 2) q 2 q 1 d. Q’ (q 1, q 2) Q’ Q Bronstein Kimmel 2006 © 2006 by Kerry R. Widder 13

Recent Work – “Partial Embedding” (PE) ØIssues • Strengths – – Reduced error/distortion. Can handle partial data. Not sensitive to preprocessing steps. No alignment step. • Limitations – Boundary issues for partial matching. – Can’t pre-compute distance function (can minimize this impact using a hierarchical search scheme). © 2006 by Kerry R. Widder 14

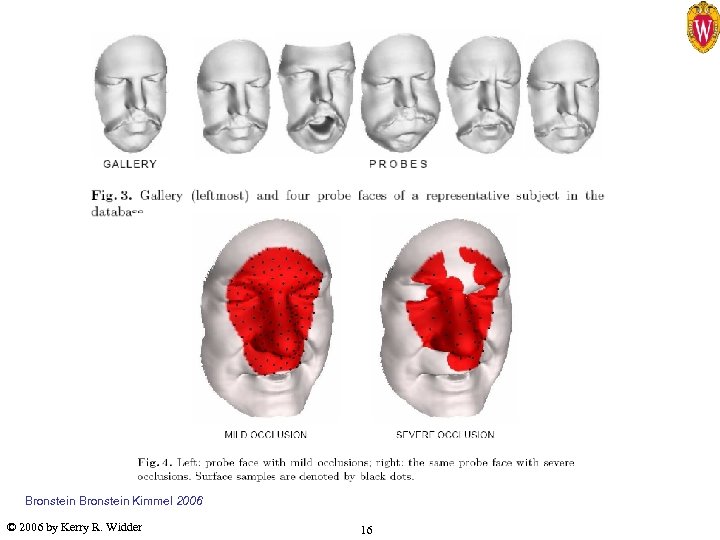
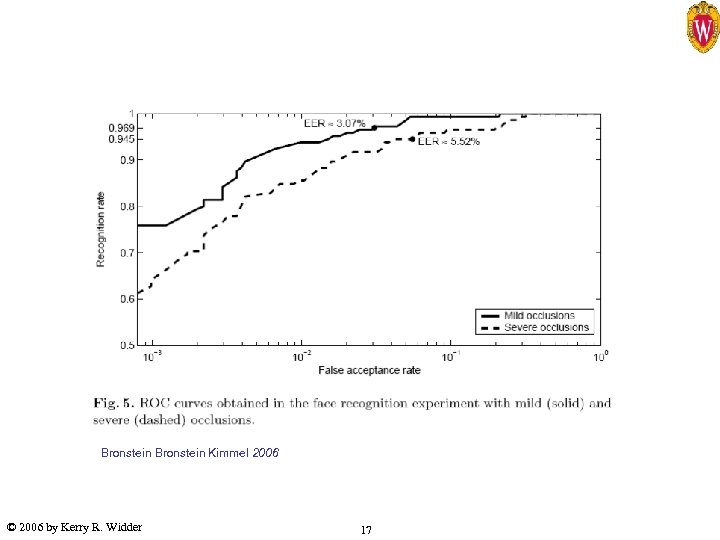
Recent Work – “Partial Embedding” (PE) ØResults • Database – FRGC data – used 30 subjects – 1 neutral expression (gallery), 5 moderate expression (probes). – Gallery images were sub-sampled at 2500 points – Probe images were sub-sampled at 53 points – Two sets of probe images created – 1. face cropped with narrow geodesic mask, 2. Severe occlusions • Results – – Mild occlusion – EER of 3. 1% Severe occlusion – EER of 5. 5% 100% rank one recognition rate Computation time: 1/5 sec. per comparison © 2006 by Kerry R. Widder 15

Bronstein Kimmel 2006 © 2006 by Kerry R. Widder 16

Bronstein Kimmel 2006 © 2006 by Kerry R. Widder 17

Future Work – “Partial Embedding” (PE) • Larger data set • More severe expressions • Extend to texture © 2006 by Kerry R. Widder 18

Selected References • A. M. Bronstein, M. M. Bronstein, and R. Kimmel. Robust expressioninvariant face recognition from partially missing data. Proc. 9 th European Conf. on Computer Vision, May 2006. • A. M. Bronstein, M. M. Bronstein, and R. Kimmel. Three-dimensional face recognition. Intl. J. Computer Vision, 64(1): 5 -30, August 2005. • A. Elad and R. Kimmel. On bending invariant signatures for surfaces. IEEE Trans. PAMI, 25(10): 1285 -1295, 2003. • A. M. Bronstein, M. M. Bronstein, and R. Kimmel. Generalized multidimensional scaling: a framework for isometry-invariant partial surface matching. Proc. Nat. Acad. Sci. , 103(5): 1168 -1172, January 2006. • A. M. Bronstein, M. M. Bronstein, and R. Kimmel. Expression-invariant representations for human faces. Technical Report CIS-2005 -01, Dept. of Computer Science, Technion, Israel, June 2005. © 2006 by Kerry R. Widder 19