 Exponential Functions, Growth and Decay Goal: Graph exponential growth and decay functions and use exponential growth and decay functions to model real-life situations.
Exponential Functions, Growth and Decay Goal: Graph exponential growth and decay functions and use exponential growth and decay functions to model real-life situations.
 Exponential Function ¡ A function in the form: Base is Constant l Exponent is the Independent Variable l
Exponential Function ¡ A function in the form: Base is Constant l Exponent is the Independent Variable l
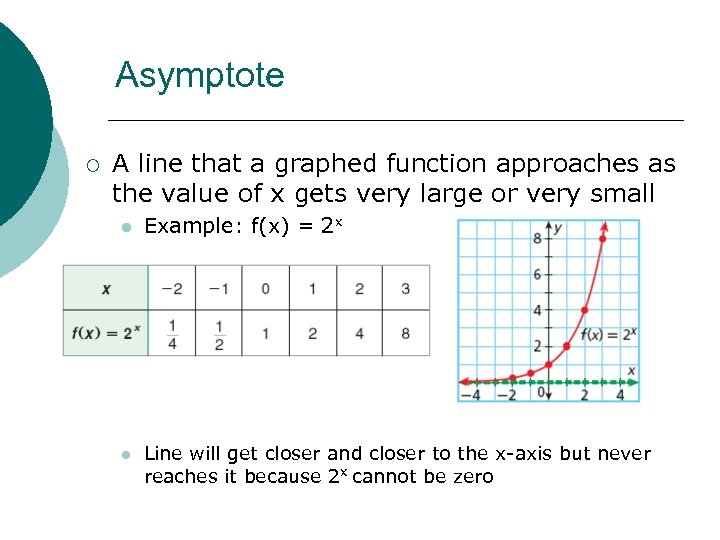 Asymptote ¡ A line that a graphed function approaches as the value of x gets very large or very small l l Example: f(x) = 2 x Line will get closer and closer to the x-axis but never reaches it because 2 x cannot be zero
Asymptote ¡ A line that a graphed function approaches as the value of x gets very large or very small l l Example: f(x) = 2 x Line will get closer and closer to the x-axis but never reaches it because 2 x cannot be zero
 Graphing Exponential Functions ¡ To graph an exponential function of the form y = abx-h+k, sketch graph of abx, then translate the graph horizontally by h units and veritcally by k units.
Graphing Exponential Functions ¡ To graph an exponential function of the form y = abx-h+k, sketch graph of abx, then translate the graph horizontally by h units and veritcally by k units.
 Graphing Exponential Functions How does this apply to real life situations? If you invested $200. 00 in an account that paid simple interest, find how long you’d need to leave it in at 4% interest to make $10. 00 In 1985, there were 285 cell phone subscribers in the small town of Centerville. The number of subscribers increased by 75% per year after 1985. How many cell phone subscribers were in Centerville in 1994? Bacteria can multiply at an alarming rate when each bacteria splits into two new cells, thus doubling. For example, if we start with only one bacteria which can double every hour, by the end of one day we will have over 16 million bacteria.
Graphing Exponential Functions How does this apply to real life situations? If you invested $200. 00 in an account that paid simple interest, find how long you’d need to leave it in at 4% interest to make $10. 00 In 1985, there were 285 cell phone subscribers in the small town of Centerville. The number of subscribers increased by 75% per year after 1985. How many cell phone subscribers were in Centerville in 1994? Bacteria can multiply at an alarming rate when each bacteria splits into two new cells, thus doubling. For example, if we start with only one bacteria which can double every hour, by the end of one day we will have over 16 million bacteria.
 Percent Increase and Decrease You can model growth or decay by a constant percent increase or percent decrease with the formula: Initial Amount A(t) = a (1 + r)t Final Amount Number of Time Periods Rate of Increase 1+r is growth factor 1 -r is decay factor
Percent Increase and Decrease You can model growth or decay by a constant percent increase or percent decrease with the formula: Initial Amount A(t) = a (1 + r)t Final Amount Number of Time Periods Rate of Increase 1+r is growth factor 1 -r is decay factor
 1. In January, 1993 , there were about 1, 313, 000 Internet hosts. During the next 5 years the number of hosts increased by about 100% per year. Step 1: Write a function to model the number h (in millions) of hosts t years after 1993. About how many hosts were there in 1996? Step 2: Graph the function. Step 3: Use the graph to estimate the year when there were 30 million hosts.
1. In January, 1993 , there were about 1, 313, 000 Internet hosts. During the next 5 years the number of hosts increased by about 100% per year. Step 1: Write a function to model the number h (in millions) of hosts t years after 1993. About how many hosts were there in 1996? Step 2: Graph the function. Step 3: Use the graph to estimate the year when there were 30 million hosts.
 2. You buy a new car for $24, 000. The value y of the car decreases by 16% each year. Step 1: Write a function to model the value of the car. Use the model to estimate the value after 2 years. Step 2: Graph the function. Step 3: Use the graph to estimate when the value of the car will have a value of $12, 000.
2. You buy a new car for $24, 000. The value y of the car decreases by 16% each year. Step 1: Write a function to model the value of the car. Use the model to estimate the value after 2 years. Step 2: Graph the function. Step 3: Use the graph to estimate when the value of the car will have a value of $12, 000.
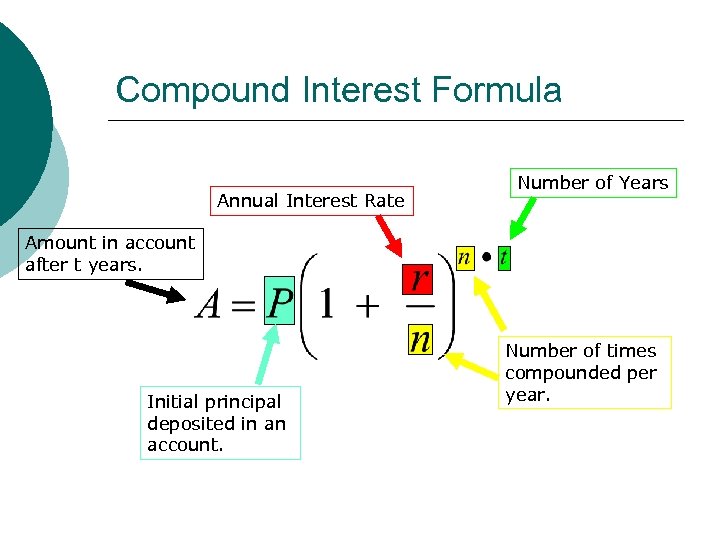 Compound Interest Formula Annual Interest Rate Number of Years Amount in account after t years. Initial principal deposited in an account. Number of times compounded per year.
Compound Interest Formula Annual Interest Rate Number of Years Amount in account after t years. Initial principal deposited in an account. Number of times compounded per year.
 1. You deposit $1, 000 in an account that pays 8% annual interest. Find the balance after 1 year if the interest is compounded with the given frequency. a. Annually a. Quarterly a. Daily
1. You deposit $1, 000 in an account that pays 8% annual interest. Find the balance after 1 year if the interest is compounded with the given frequency. a. Annually a. Quarterly a. Daily
 2. You deposit $1, 600 in a band account. Find the balance after 3 years if the account pays 2. 5% annual interest compounded monthly. 3. What if the account paid 1. 75% annual interest compounded quarterly?
2. You deposit $1, 600 in a band account. Find the balance after 3 years if the account pays 2. 5% annual interest compounded monthly. 3. What if the account paid 1. 75% annual interest compounded quarterly?