25d887b5f81390192d717547acea50df.ppt
- Количество слайдов: 98
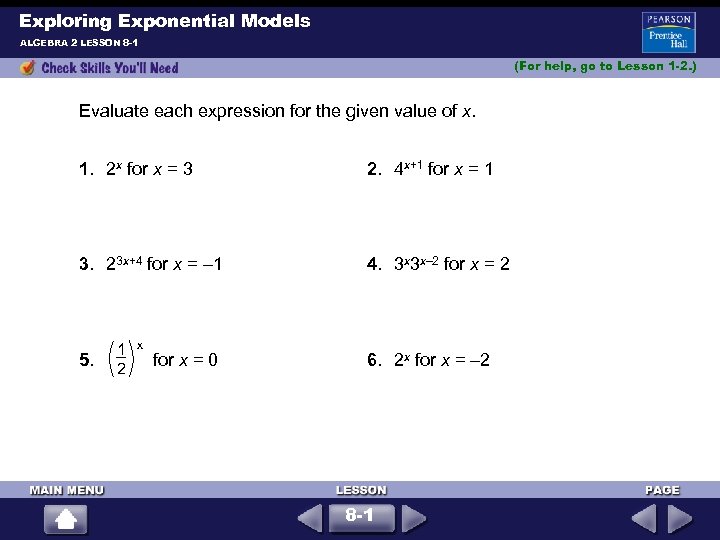
Exploring Exponential Models ALGEBRA 2 LESSON 8 -1 (For help, go to Lesson 1 -2. ) Evaluate each expression for the given value of x. 1. 2 x for x = 3 2. 4 x+1 for x = 1 3. 23 x+4 for x = – 1 4. 3 x 3 x– 2 for x = 2 1 x 5. for x = 0 2 6. 2 x for x = – 2 8 -1
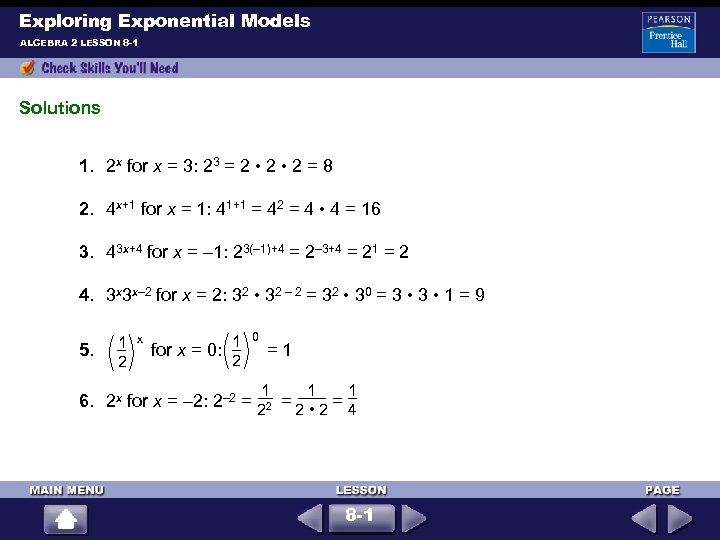
Exploring Exponential Models ALGEBRA 2 LESSON 8 -1 Solutions 1. 2 x for x = 3: 23 = 2 • 2 = 8 2. 4 x+1 for x = 1: 41+1 = 42 = 4 • 4 = 16 3. 43 x+4 for x = – 1: 23(– 1)+4 = 2– 3+4 = 21 = 2 4. 3 x 3 x– 2 for x = 2: 32 • 32 – 2 = 32 • 30 = 3 • 1 = 9 1 0 1 x 5. for x = 0: = 1 2 2 1 1 1 6. 2 x for x = – 2: 2– 2 = = = 4 22 2 • 2 8 -1
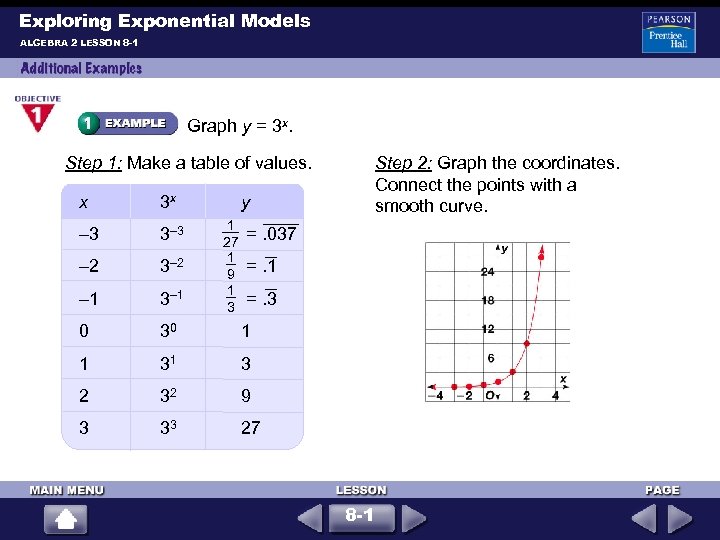
Exploring Exponential Models ALGEBRA 2 LESSON 8 -1 Graph y = 3 x. Step 1: Make a table of values. x 3 x y – 3 3– 3 – 2 3– 2 – 1 3– 1 0 30 1 1 31 3 2 32 9 3 33 Step 2: Graph the coordinates. Connect the points with a smooth curve. 27 1 =. 037 27 1 9 =. 1 1 =. 3 3 8 -1
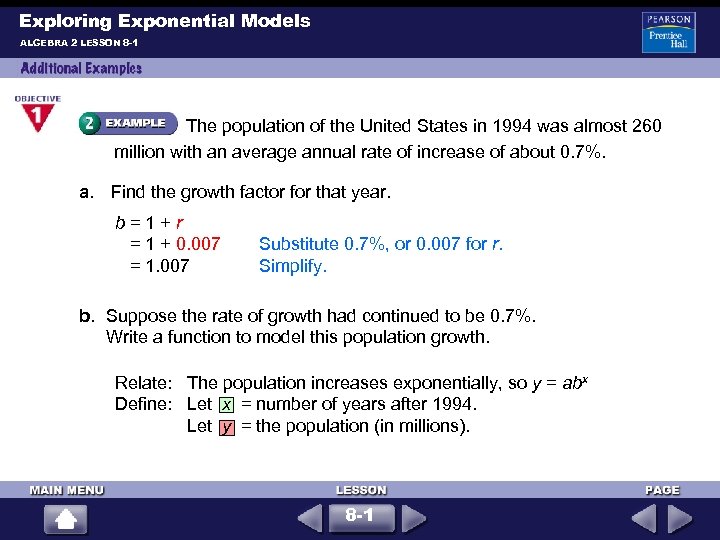
Exploring Exponential Models ALGEBRA 2 LESSON 8 -1 The population of the United States in 1994 was almost 260 million with an average annual rate of increase of about 0. 7%. a. Find the growth factor for that year. b = 1 + r = 1 + 0. 007 = 1. 007 Substitute 0. 7%, or 0. 007 for r. Simplify. b. Suppose the rate of growth had continued to be 0. 7%. Write a function to model this population growth. Relate: The population increases exponentially, so y = abx Define: Let x = number of years after 1994. Let y = the population (in millions). 8 -1
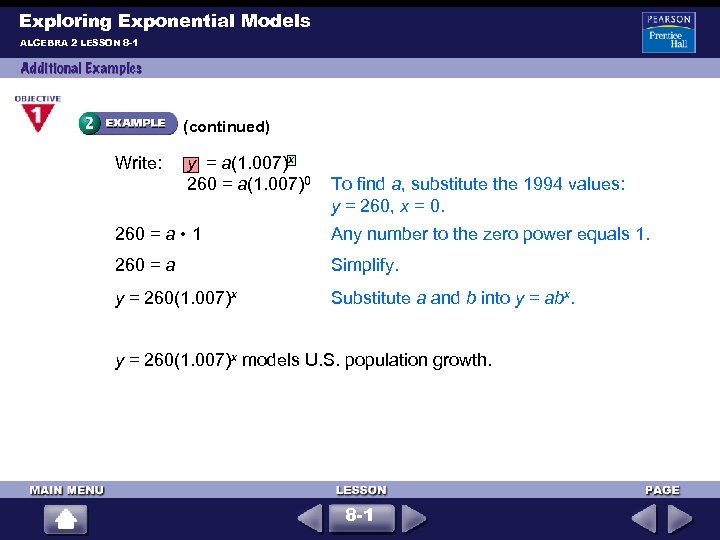
Exploring Exponential Models ALGEBRA 2 LESSON 8 -1 (continued) Write: y = a(1. 007)x 260 = a(1. 007)0 To find a, substitute the 1994 values: y = 260, x = 0. 260 = a • 1 Any number to the zero power equals 1. 260 = a Simplify. y = 260(1. 007)x Substitute a and b into y = abx. y = 260(1. 007)x models U. S. population growth. 8 -1

Exploring Exponential Models ALGEBRA 2 LESSON 8 -1 Write an exponential function y = abx for a graph that includes (1, 6) and (0, 2). y = abx Use the general term. 6 = ab 1 Substitute for x and y using (1, 6). 6 = a b Solve for a. 6 b 6 2 = b 0 Substitute for x and y using (0, 2) and for a using . 6 b 6 2 = b Any number to the zero power equals 1. b = 3 Solve for b. b 2 = • 1 Simplify. 8 -1
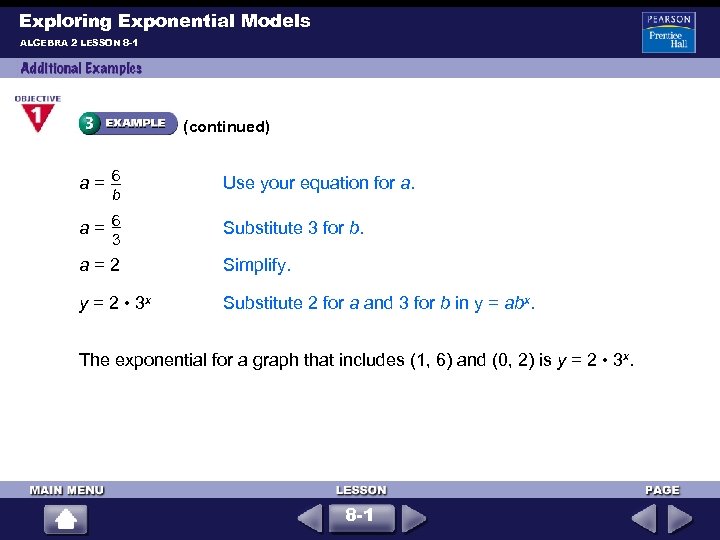
Exploring Exponential Models ALGEBRA 2 LESSON 8 -1 (continued) a = 6 Use your equation for a. a = 6 Substitute 3 for b. a = 2 Simplify. y = 2 • 3 x Substitute 2 for a and 3 for b in y = abx. b 3 The exponential for a graph that includes (1, 6) and (0, 2) is y = 2 • 3 x. 8 -1

Exploring Exponential Models ALGEBRA 2 LESSON 8 -1 2 x Without graphing, determine whether the function y = 3 3 represents exponential growth or decay. 2 x 2 In y = , b = . 3 3 3 Since b < 1, the function represents exponential decay. 8 -1
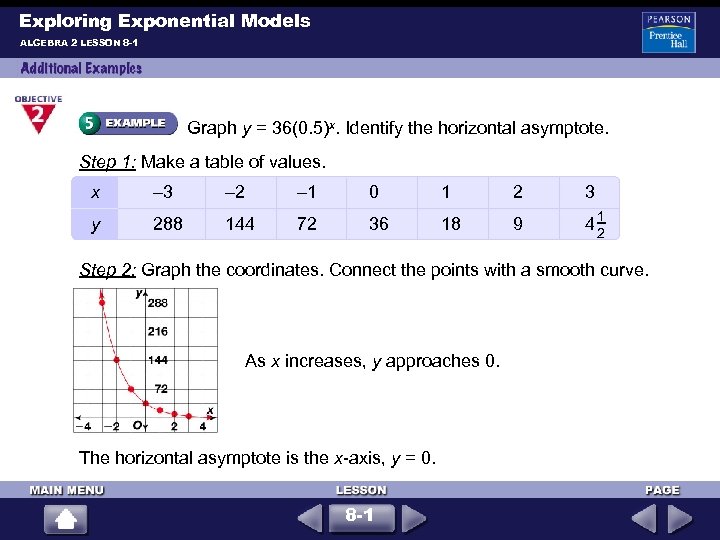
Exploring Exponential Models ALGEBRA 2 LESSON 8 -1 Graph y = 36(0. 5)x. Identify the horizontal asymptote. Step 1: Make a table of values. x – 3 – 2 – 1 0 1 2 3 y 288 144 72 36 18 9 41 2 Step 2: Graph the coordinates. Connect the points with a smooth curve. As x increases, y approaches 0. The horizontal asymptote is the x-axis, y = 0. 8 -1

Exploring Exponential Models ALGEBRA 2 LESSON 8 -1 Suppose you want to buy a used car that costs $11, 800. The expected depreciation of the car is 20% per year. Estimate the depreciated value of the car after 6 years. The decay factor b = 1 + r, where r is the annual rate of change. b = 1 + r Use r to find b. = 1 + (– 0. 20) = 0. 80 Simplify. Write an equation, and then evaluate it for x = 6. Relate: The value of the car decreases exponentially; b = 0. 8. Define: Let x = number of years. Let y = value of the car. 8 -1
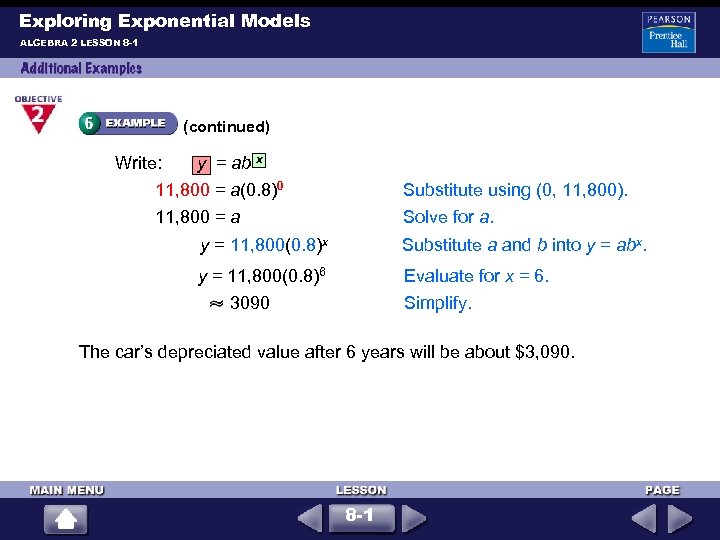
Exploring Exponential Models ALGEBRA 2 LESSON 8 -1 (continued) Write: y = ab x 11, 800 = a(0. 8)0 11, 800 = a Substitute using (0, 11, 800). Solve for a. y = 11, 800(0. 8)x Substitute a and b into y = abx. y = 11, 800(0. 8)6 Evaluate for x = 6. 3090 Simplify. The car’s depreciated value after 6 years will be about $3, 090. 8 -1
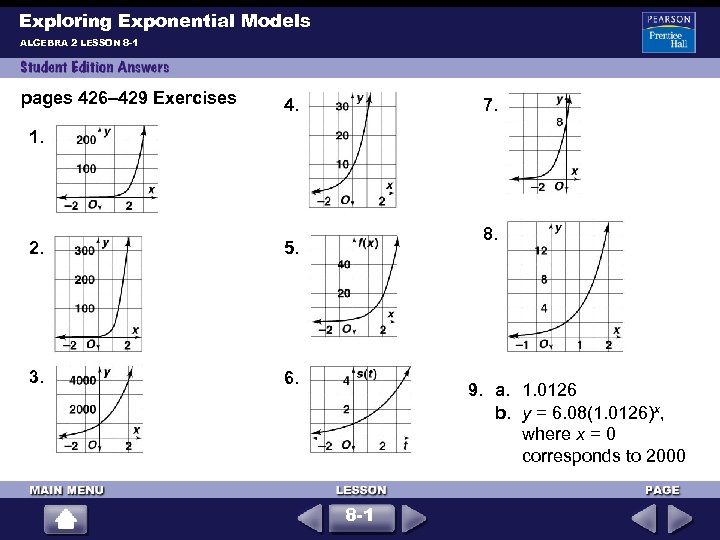
Exploring Exponential Models ALGEBRA 2 LESSON 8 -1 pages 426– 429 Exercises 4. 7. 1. 2. 5. 3. 8. 6. 9. a. 1. 0126 b. y = 6. 08(1. 0126)x, where x = 0 corresponds to 2000 8 -1
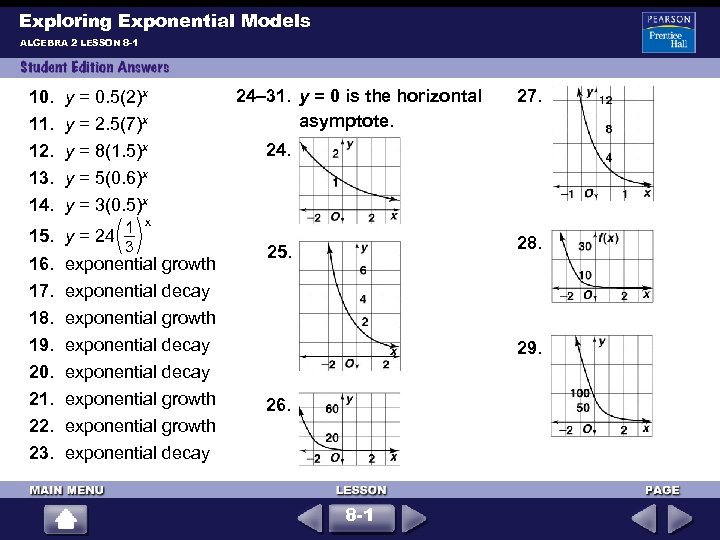
Exploring Exponential Models ALGEBRA 2 LESSON 8 -1 10. y = 0. 5(2)x 11. y = 2. 5(7)x 12. y = 8(1. 5)x 24– 31. y = 0 is the horizontal asymptote. 27. 24. 13. y = 5(0. 6)x 14. y = 3(0. 5)x 1 15. y = 24 3 16. 17. 18. 19. 20. 21. 22. 23. x exponential growth exponential decay exponential growth exponential decay 28. 25. 29. 26. 8 -1
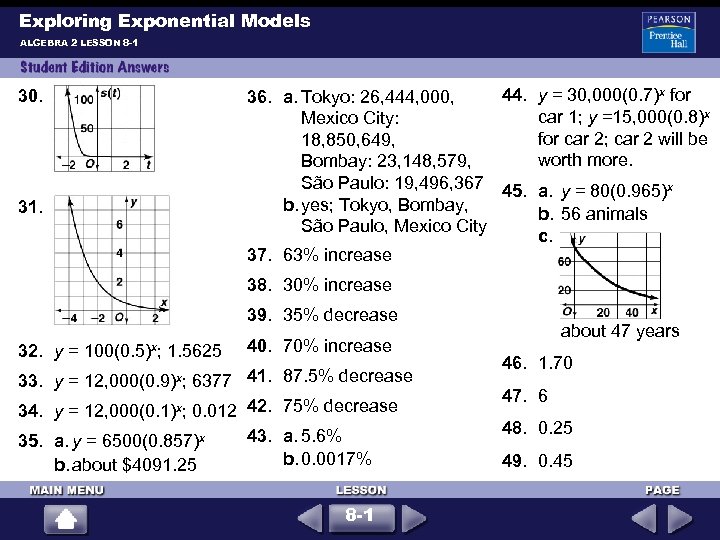
Exploring Exponential Models ALGEBRA 2 LESSON 8 -1 44. y = 30, 000(0. 7)x for 36. a. Tokyo: 26, 444, 000, car 1; y =15, 000(0. 8)x Mexico City: for car 2; car 2 will be 18, 850, 649, worth more. Bombay: 23, 148, 579, São Paulo: 19, 496, 367 45. a. y = 80(0. 965)x b. yes; Tokyo, Bombay, b. 56 animals São Paulo, Mexico City c. 37. 63% increase 30. 31. 38. 30% increase 39. 35% decrease 32. y = 100(0. 5)x; 1. 5625 40. 70% increase 33. y = 12, 000(0. 9)x; 6377 41. 87. 5% decrease 34. y = 12, 000(0. 1)x; 0. 012 42. 75% decrease 35. a. y = 6500(0. 857)x b. about $4091. 25 43. a. 5. 6% b. 0. 0017% 8 -1 about 47 years 46. 1. 70 47. 6 48. 0. 25 49. 0. 45

Exploring Exponential Models ALGEBRA 2 LESSON 8 -1 50. 1. 125 51. 0. 999 52. 1. 001 53. 2 59. a. A negative growth rate would be represented by adding the negative rate to 1. b. Armenia: y = 9. 2(1. 06)x, 54. y = 34(1. 26)x, where x represents the number of years since 1995. 55. Check students’ work. 56. about $42, 140 57. C 58. B; the graph shows a c. decreasing function, so b < 1, which eliminates A. The graph is always positive, which eliminates C. Canada: y = 688. 3(1. 03)x, 60. C 61. H 62. B 63. [2] Oman: y = 18. 6(. 915)x, Paraguay: y = 19. 8(. 995)x, x in each equation represents the number of years since 1998. Armenia: $13. 8 billion, Canada: $846. 5 billion, Oman: $10. 0 billion, Paraguay: $19. 1 billion 8 -1 [1] general form of graph correct, but not exact
![Exploring Exponential Models ALGEBRA 2 LESSON 8 -1 64. [4]y = abx 54 = Exploring Exponential Models ALGEBRA 2 LESSON 8 -1 64. [4]y = abx 54 =](https://present5.com/presentation/25d887b5f81390192d717547acea50df/image-16.jpg)
Exploring Exponential Models ALGEBRA 2 LESSON 8 -1 64. [4]y = abx 54 = ab 2 54 b 2 1 54 2 = b 2 54 a = 2= 3 2 3 b 2 2 b = 54 65. [3] appropriate methods 67. with one computational error [2] starts problem correctly, but fails to finish it properly [1] correct answer, 68. 6 n 2 5 n 3 without work shown 69. 84 r 2 9 r 2 3 2 b = 27 2 b = 27 3 b = 9 54 a = 92 70. 2 x 3 x 71. Answers may vary. Sample: y = x 3 – 5 x 2 + 4 x 72. Answers may vary. Sample: y = x 3 – 7 x – 6 66. 2 a= 3 2 y = 3 9 x 8 -1
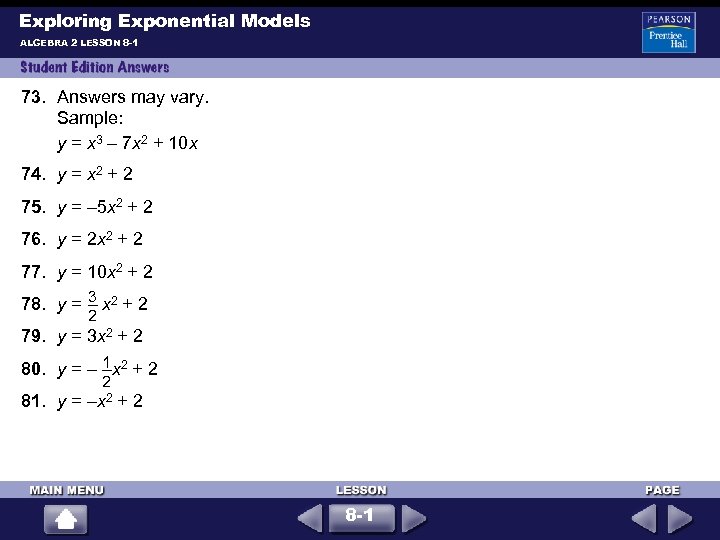
Exploring Exponential Models ALGEBRA 2 LESSON 8 -1 73. Answers may vary. Sample: y = x 3 – 7 x 2 + 10 x 74. y = x 2 + 2 75. y = – 5 x 2 + 2 76. y = 2 x 2 + 2 77. y = 10 x 2 + 2 3 78. y = x 2 + 2 2 79. y = 3 x 2 + 2 1 80. y = – x 2 + 2 2 81. y = –x 2 + 2 8 -1
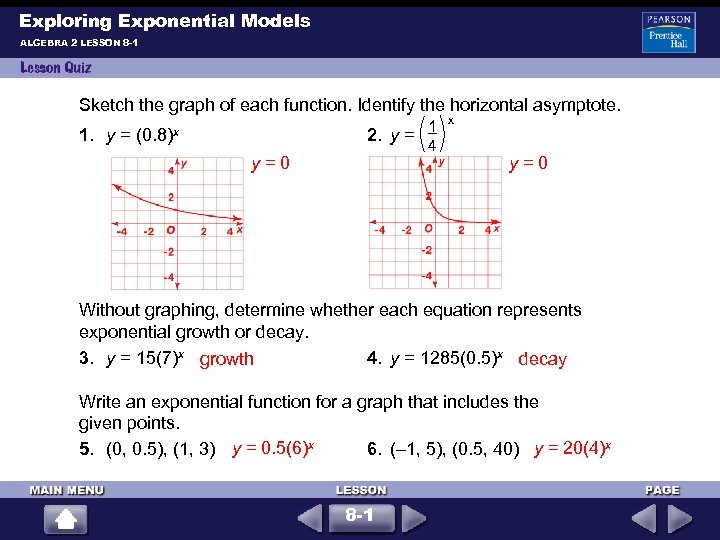
Exploring Exponential Models ALGEBRA 2 LESSON 8 -1 Sketch the graph of each function. Identify the horizontal asymptote. 1. y = (0. 8)x y = 0 1 2. y = 4 x y = 0 Without graphing, determine whether each equation represents exponential growth or decay. 3. y = 15(7)x growth 4. y = 1285(0. 5)x decay Write an exponential function for a graph that includes the given points. 5. (0, 0. 5), (1, 3) y = 0. 5(6)x 6. (– 1, 5), (0. 5, 40) y = 20(4)x 8 -1

Properties of Exponential Functions ALGEBRA 2 LESSON 8 -2 (For help, go to Lesson 2 -6, 5 -3, and 7 -4. ) Write an equation for each translation. 1. y = | x |, 1 unit up, 2 units left 2. y = –| x |, 2 units down 3. y = x 2, 2 units down, 1 unit right 4. y = –x 2, 3 units up, 1 unit left Write each equation in simplest form. Assume that all variables are positive. 5. y = x – 5 4 4 6. y = x – 1 – 7 7 7. y = x 5 6 6 8. Use the formula for simple interest I = Prt. Find the interest for a principal of $550 at a rate of 3% for 2 years. 8 -2

Properties of Exponential Functions ALGEBRA 2 LESSON 8 -2 Solutions 1. y = | x |, 1 unit up and 2 units left: y = | x + 2 | + 1 2. y = –| x |, 2 units down: y = –| x | – 2 3. y = x 2, 2 units down and 1 unit right: y = (x – 1)2 – 2 4. y = –x 2, 3 units up and 1 unit left: y = –(x + 1)2 + 3 5. 5 5 4 – (4) 4 4 y = x ; y = x– 5 or y = – 6. y = x 7. 1 – 7 – 1 (– 7) 7 7 ; y = x 1; y = x 1 x 5 – 5 5 6 6 y = x ; y = x 6 (6); y = x 5 8. I = Prt = $550(0. 03)(2) = $16. 50(2) = $33 8 -2
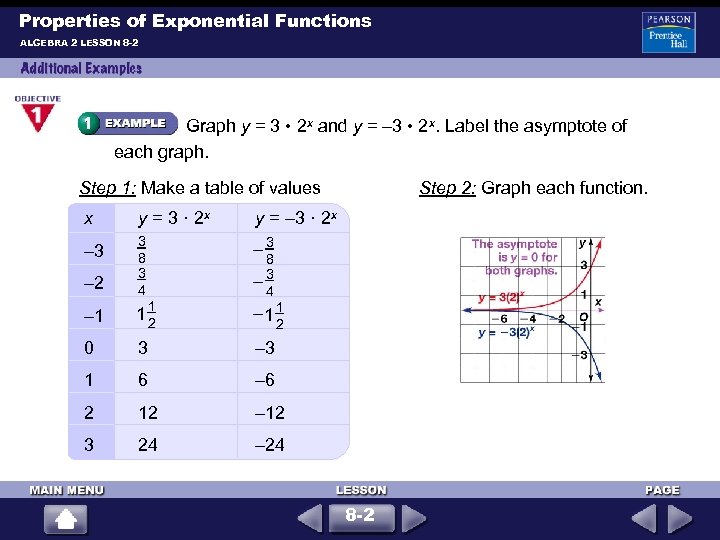
Properties of Exponential Functions ALGEBRA 2 LESSON 8 -2 Graph y = 3 • 2 x and y = – 3 • 2 x. Label the asymptote of each graph. Step 1: Make a table of values x y = 3 · 2 x y = – 3 · 2 x – 3 – 2 3 8 3 4 – 1 12 – 1 1 0 3 – 3 1 6 – 6 2 12 – 12 3 24 Step 2: Graph each function. – 24 1 8 – 3 4 2 8 -2
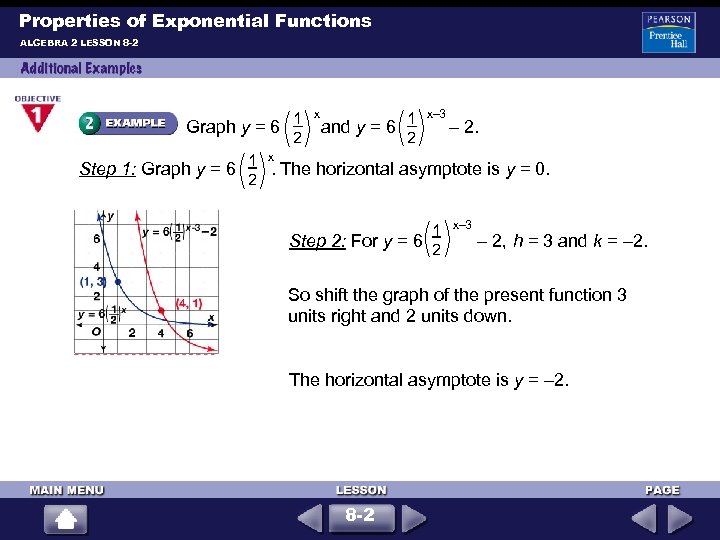
Properties of Exponential Functions ALGEBRA 2 LESSON 8 -2 1 x– 3 1 x Graph y = 6 and y = 6 – 2. 2 2 x Step 1: Graph y = 6 1. The horizontal asymptote is y = 0. 2 1 x– 3 Step 2: For y = 6 – 2, h = 3 and k = – 2. 2 So shift the graph of the present function 3 units right and 2 units down. The horizontal asymptote is y = – 2. 8 -2

Properties of Exponential Functions ALGEBRA 2 LESSON 8 -2 Since a 100 -mg supply of technetium-99 m has a half-life of 6 hours, find the amount of technetium-99 m that remains from a 50 mg supply after 25 hours. Relate: The amount of technetium-99 m is an exponential function of the number of half-lives. The initial amount is 50 mg. The decay 1 2 factor is . One half-life equals 6 h. Define: Let y = the amount of technetium-99 m. Let x = the number of hours elapsed. 1 Then x = the number of half-lives. 6 8 -2

Properties of Exponential Functions ALGEBRA 2 LESSON 8 -2 (continued) Write: y = 50 1 2 1 x 6 1 • 25 6 1 4. 16 = 50 2 Substitute 25 for x. Simplify. 2. 784 After 25 hours, about 2. 784 mg of technetium-99 m remains. 8 -2

Properties of Exponential Functions ALGEBRA 2 LESSON 8 -2 Graph y = ex. Evaluate e 3 to four decimal places. Step 1: Graph y = ex. Step 2: Find y when x = 3. The value of e 3 is about 20. 0855. 8 -2
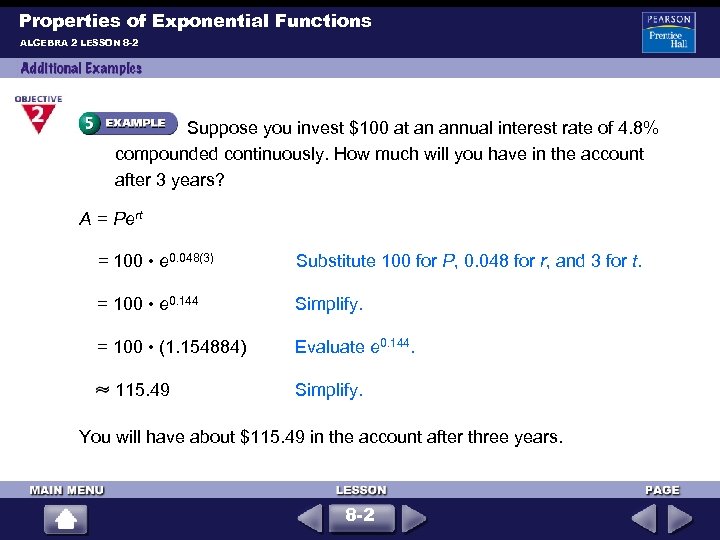
Properties of Exponential Functions ALGEBRA 2 LESSON 8 -2 Suppose you invest $100 at an annual interest rate of 4. 8% compounded continuously. How much will you have in the account after 3 years? A = Pert = 100 • e 0. 048(3) Substitute 100 for P, 0. 048 for r, and 3 for t. = 100 • e 0. 144 Simplify. = 100 • (1. 154884) Evaluate e 0. 144. 115. 49 Simplify. You will have about $115. 49 in the account after three years. 8 -2
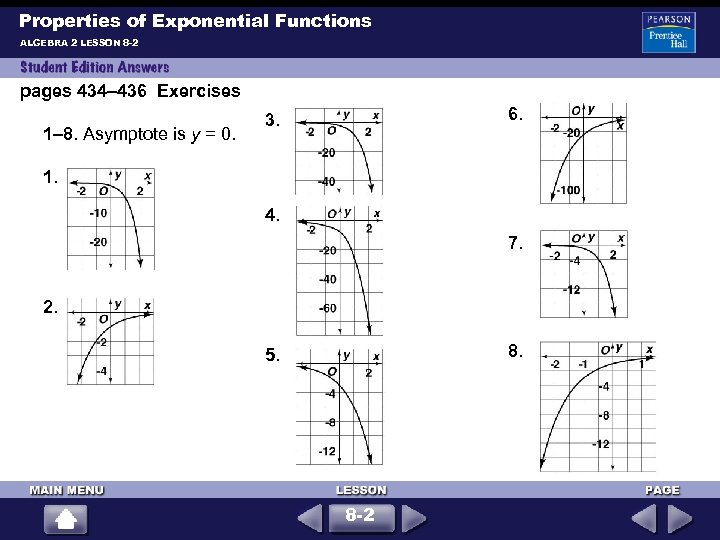
Properties of Exponential Functions ALGEBRA 2 LESSON 8 -2 pages 434– 436 Exercises 1– 8. Asymptote is y = 0. 6. 3. 1. 4. 7. 2. 8. 5. 8 -2
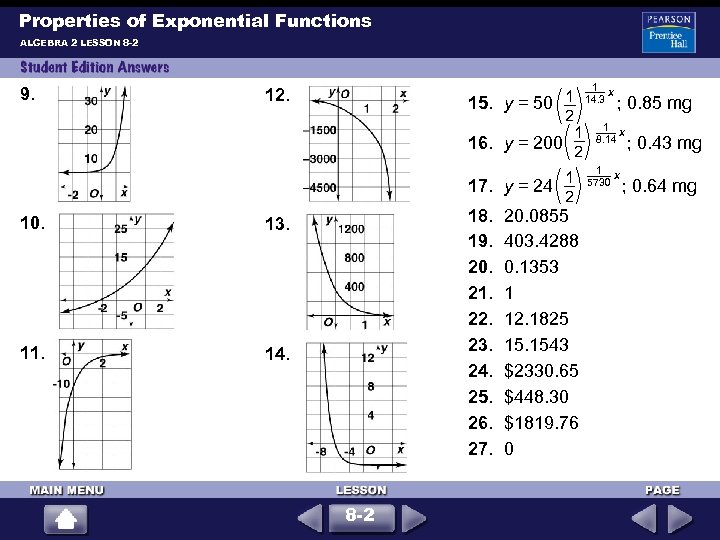
Properties of Exponential Functions ALGEBRA 2 LESSON 8 -2 9. 1 12. 1 14. 3 x 15. y = 50 ; 0. 85 mg 2 1 1 8. 14 x 16. y = 200 ; 0. 43 mg 2 1 1 5730 x 17. y = 24 ; 0. 64 mg 2 10. 11. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 13. 14. 8 -2 20. 0855 403. 4288 0. 1353 1 12. 1825 15. 1543 $2330. 65 $448. 30 $1819. 76 0

Properties of Exponential Functions ALGEBRA 2 LESSON 8 -2 28. 1 c. The graph of exponential 29. If c < 0, the graph models decay approaches the exponential decay. If asymptote y = 0 as x c = 0, the graph is a increases. The graph horizontal line. If c > 0, of negative the graph models exponential growth. approaches the 30. $6168. 41 asymptote y = 0 as x decreases. 31. a. Answers may vary. Sample: y = – 2(1. 3)x 1 x 32. y = 4 ; b. Answers may vary. 2 1 x + 4 Sample: I am in debt y = 4 + 3 2 for $2 and my debt is 33. y = – 3 x; growing at a rate of 30% per year. y = – 3 x– 8 + 2 8 -2 1 y = (2)x– 6 – 7 2 1 x 35. y = – 3 ; 3 1 x + 5 y = – 3 – 1 3 34. y = (2)x; 36. 75. 0 pascals 37. 8. 7 yr 38. A deficit that is growing exponentially is modeled by y = abcx, where a < 0, and either b > 1 and c > 0 or 0 < b < 1 and c < 0.

Properties of Exponential Functions ALGEBRA 2 LESSON 8 -2 39. a. GDP = 8. 511(1. 038)t where t = 0 corresponds to 1998 and 8. 511 is trillions. b. It almost doubles. (about 195. 7%) c. In 9 years, the growth is about 40%. 40. a. $2501. 50 b. $3. 15 more 41. $399. 97 42. exponential growth 43. exponential growth 44. exponential decay 45. exponential growth 46. exponential decay b. Graphically, it will never happen; the 47. exponential growth graph has y = 30 as an asymptote. (In reality, you 48. a. y = 8001 – 3 x, where would be close to y is the number of knowing all the uninfected people names in about 21 and x represents days. ) days. b. 5814 people c. about 9 days 49. a. about 10 names; about 24 names 8 -2 c. Answers may vary. Sample: I learn names pretty quickly; my learning rate might be 0. 4.

Properties of Exponential Functions ALGEBRA 2 LESSON 8 -2 50. a. 2928 m 3 b. V = 2928 – 15(2 x – 1) c. ninth weekend 51. A 52. I 58. 59. 60. 61. 53. C 54. F 55. [2] A = Pert 8000 = Pe(0. 06)(4) 63. – 8000 e = P (0. 06)(4) P = $6293. 02 [1] answer only, without work shown 56. y = 3 x 57. y = – 2(4)x y = – 5(2)x y = 8(0. 5)x y = 70(10)x y = 10, 000(0. 8)x 62. 6 5 3 4 64. 5( ) 3 + 5 65. 2( 4 4 2 + 8 ) 66. 3 67. 11 7 71. x 2 – x – 6 72. x 2 – 1 73. x 2 + x + 1 74. 13 x + 1 75. 3 x 2 – 7 x + 2 76. x – y = 5, x + z = 5, –y + z = 5 77. x + y = – 2, x + 4 z = – 2, y + 4 z = – 2 68. 15 – 6 6 69. 3 + 5 70. x – 3, R – 1 8 -2 78. x + y = 8, x – 2 z = 8, y – 2 z = 8

Properties of Exponential Functions ALGEBRA 2 LESSON 8 -2 79. x – y = 8, x + 2 z = 8, –y + 2 z = 8 80. 3 x + y = – 18, x + 3 z = – 6, y + 9 z = – 18 81. – 2 x + y = 10, – 2 x – 5 z = 10, y – 5 z = 10 8 -2

Properties of Exponential Functions ALGEBRA 2 LESSON 8 -2 Describe how the graph of each function relates to its parent function. Then graph the function. 1. y = – 5 x – 1 2. y = 3(5)x – 2 + 1 reflected over the x-axis and translated down 1 rises more steeply, is translated 2 to the right and up 1 3. Use the formula A = Pert to find the amount in a continuously compounded account where the principal is $2000 at an annual interest rate of 5% for 3 years. about $2324 1 3 4. Use the graph of y = ex to evaluate e to four decimal places. 1. 3956 8 -2
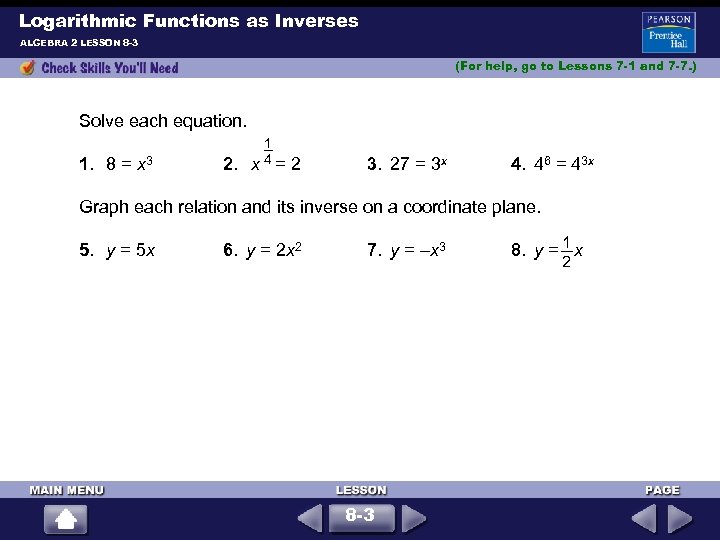
Logarithmic Functions as Inverses ALGEBRA 2 LESSON 8 -3 (For help, go to Lessons 7 -1 and 7 -7. ) Solve each equation. 1. 8 = x 3 2. 1 4 x = 2 3. 27 = 3 x 4. 46 = 43 x Graph each relation and its inverse on a coordinate plane. 5. y = 5 x 6. y = 2 x 2 7. y = –x 3 8 -3 1 8. y = x 2

Logarithmic Functions as Inverses ALGEBRA 2 LESSON 8 -3 Solutions 1. 8 = x 3; since 23 = 8, x = 2 1 4 4 2. x = 2; since 16 = = 2, x = 16 16 3. 27 = 3 x; since 33 = 27, x = 3 4. 46 = 43 x; since 6 = 3(2), x = 2 5. y = 5 x Inverse: x = 5 y 1 y = x 6. y = 2 x 2 Inverse: x = 2 y 2 x y 2 = 2 y 2 = ± 5 7. y = –x 3 Inverse: x = –y 3 = –x y = 3 –x 1 8. y = x 2 Inverse: 1 x = y 2 y = 2 x 8 -3 x 2
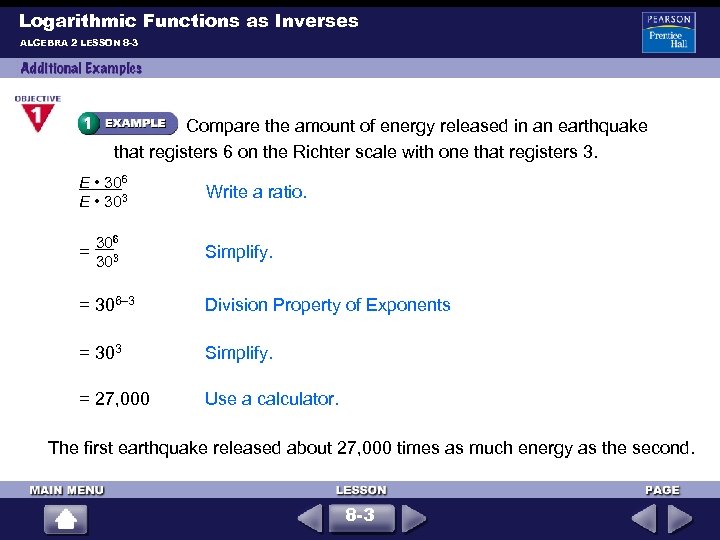
Logarithmic Functions as Inverses ALGEBRA 2 LESSON 8 -3 Compare the amount of energy released in an earthquake that registers 6 on the Richter scale with one that registers 3. E • 306 E • 303 Write a ratio. 306 = 303 Simplify. = 306– 3 Division Property of Exponents = 303 Simplify. = 27, 000 Use a calculator. The first earthquake released about 27, 000 times as much energy as the second. 8 -3
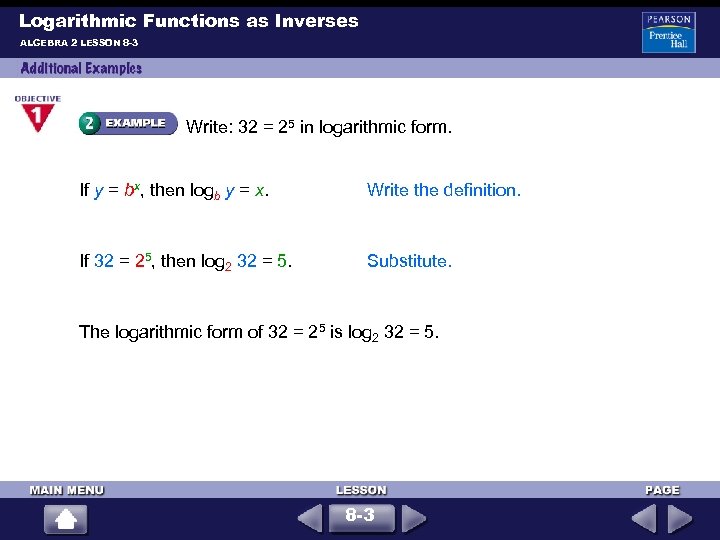
Logarithmic Functions as Inverses ALGEBRA 2 LESSON 8 -3 Write: 32 = 25 in logarithmic form. If y = bx, then logb y = x. Write the definition. If 32 = 25, then log 2 32 = 5. Substitute. The logarithmic form of 32 = 25 is log 2 32 = 5. 8 -3
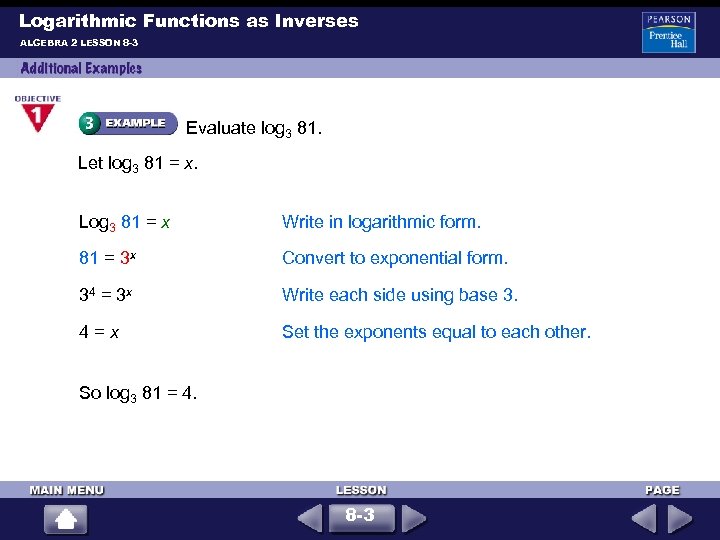
Logarithmic Functions as Inverses ALGEBRA 2 LESSON 8 -3 Evaluate log 3 81. Let log 3 81 = x. Log 3 81 = x Write in logarithmic form. 81 = 3 x Convert to exponential form. 34 = 3 x Write each side using base 3. 4 = x Set the exponents equal to each other. So log 3 81 = 4. 8 -3

Logarithmic Functions as Inverses ALGEBRA 2 LESSON 8 -3 The p. H of an apple is about 3. 3 and that of a banana is about 5. 2. Recall that the p. H of a substance equals –log[H+], where [H+] is the concentration of hydrogen ions in each fruit. Which is more acidic? Banana Apple p. H = –log[H+] 3. 3 = –log[H+] = – 3. 3 [H+] = 10– 3. 3 p. H = –log[H+] 5. 2 = –log[H+] = – 5. 2 [H+] = 10– 5. 2 5. 0 10– 4 6. 3 10– 6 The [H+] of the banana is The [H+] of the apple is about 6. 3 10– 6. 5. 0 10– 4. The apple has a higher concentration of hydrogen ions, so it is more acidic. 8 -3
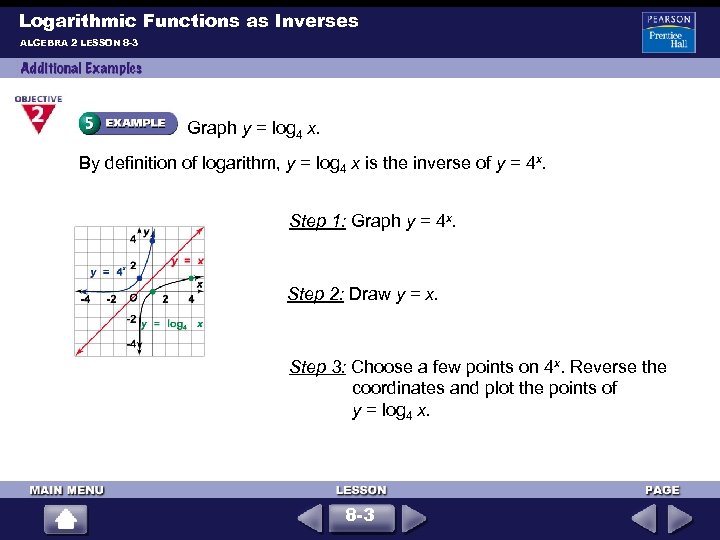
Logarithmic Functions as Inverses ALGEBRA 2 LESSON 8 -3 Graph y = log 4 x. By definition of logarithm, y = log 4 x is the inverse of y = 4 x. Step 1: Graph y = 4 x. Step 2: Draw y = x. Step 3: Choose a few points on 4 x. Reverse the coordinates and plot the points of y = log 4 x. 8 -3
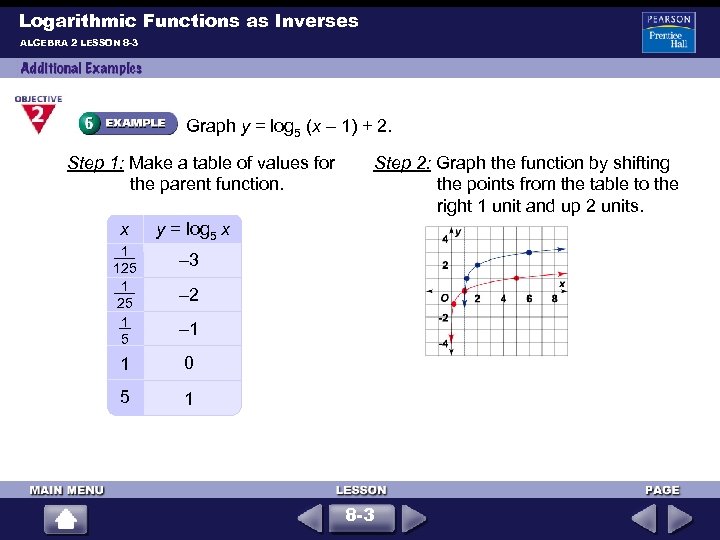
Logarithmic Functions as Inverses ALGEBRA 2 LESSON 8 -3 Graph y = log 5 (x – 1) + 2. Step 1: Make a table of values for the parent function. x y = log 5 x 1 125 1 5 – 3 1 0 5 Step 2: Graph the function by shifting the points from the table to the right 1 unit and up 2 units. 1 – 2 – 1 8 -3

Logarithmic Functions as Inverses ALGEBRA 2 LESSON 8 -3 pages 441– 444 Exercises 1. The earthquake in Missouri released about 1. 97 times more energy. 2. The earthquake in Chile released about 231 times more energy. 3. The earthquake in Missouri released about 8, 759, 310 times more energy. 4. The earthquake in Missouri released about 30 times more energy. 13. – 2 = log 0. 01 5. The earthquake in Alaska released about 83 times more energy. 14. 4 6. log 7 49 = 2 16. 1 7. 3 = log 1000 8. log 5 625 = 4 9. 1 log = – 1 10 15. 1 2 17. 3 2 18. 3 19. 1 2 20. undefined 10. 2 = log 8 64 21. 2 1 11. log 4 = – 2 22. 5 1 12. 3 = log ( ) 1 23. 1 2 3 27 24. 4 25. 3 8 -3
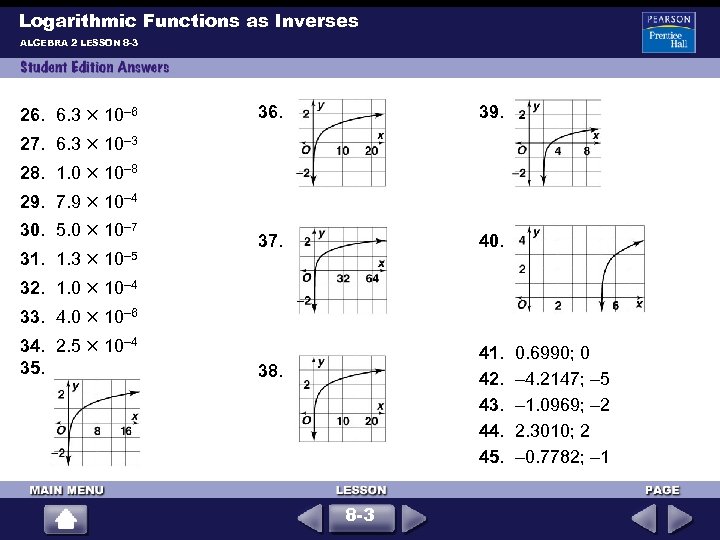
Logarithmic Functions as Inverses ALGEBRA 2 LESSON 8 -3 26. 6. 3 10– 6 36. 39. 37. 40. 27. 6. 3 10– 3 28. 1. 0 10– 8 29. 7. 9 10– 4 30. 5. 0 10– 7 31. 1. 3 10– 5 32. 1. 0 10– 4 33. 4. 0 10– 6 34. 2. 5 10– 4 35. 41. 42. 43. 44. 45. 38. 8 -3 0. 6990; 0 – 4. 2147; – 5 – 1. 0969; – 2 2. 3010; 2 – 0. 7782; – 1
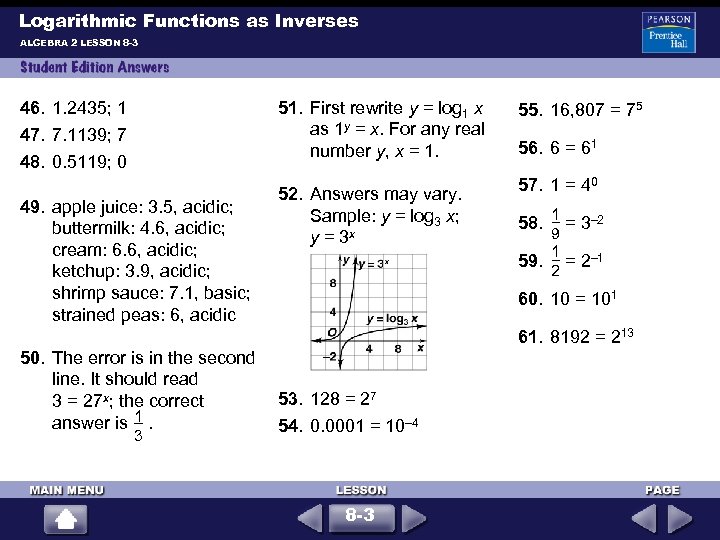
Logarithmic Functions as Inverses ALGEBRA 2 LESSON 8 -3 51. First rewrite y = log 1 x as 1 y = x. For any real number y, x = 1. 46. 1. 2435; 1 47. 7. 1139; 7 48. 0. 5119; 0 49. apple juice: 3. 5, acidic; buttermilk: 4. 6, acidic; cream: 6. 6, acidic; ketchup: 3. 9, acidic; shrimp sauce: 7. 1, basic; strained peas: 6, acidic 55. 16, 807 = 75 52. Answers may vary. Sample: y = log 3 x; y = 3 x 57. 1 = 40 56. 6 = 61 1 9 1 59. = 2– 1 2 58. = 3– 2 60. 10 = 101 61. 8192 = 213 50. The error is in the second line. It should read 53. 128 = 27 3 = 27 x; the correct 1 answer is . 54. 0. 0001 = 10– 4 3 8 -3

Logarithmic Functions as Inverses ALGEBRA 2 LESSON 8 -3 62. a. buffalo bone: 9826 to 10, 128 years old, bone fragment: 9776 to 10, 180 years old, pottery shard: 0 to 183 years old, charcoal: 9718 to 10, 242 years old, spear shaft: 9776 to 10, 263 years old b. The pottery shard; answers may vary. Samples: the pottery may be from a later civilization, or the mass or the beta radiation emissions may have been measured incorrectly. 63. y = 4 x 73. 64. y = 0. 5 x 65. y = 10 x 66. y = 2 x– 1 67. y = 10 x – 1 74. 68. y = 10 x– 1 69. y = 10 x + 2 70. y = 5 x 2 71. y = 3 1 x 72. 75. domain {x|x > 0}, range: all reals 76. domain {x|x > 0}, range: all reals 8 -3

Logarithmic Functions as Inverses ALGEBRA 2 LESSON 8 -3 77. domain {x|x > 3}, range: all reals 78. domain {x|x > 0}, range: all reals 79. domain {x|x > 2}, range: all reals 80. domain {x|x > – 1}, range: all reals 81. domain {x|x > 0}, range: all reals 82. domain {x|x > 0}, range: all reals 83. domain {x|x > t }, range: all reals 84. 100 91. D 85. 70 92. I 86. 60 93. C 87. 20 94. A 88. 10 95. B 89. a. III 96. C b. I c. IV d. 90. a. b. c. 97. II II I y = – 100 8 -3
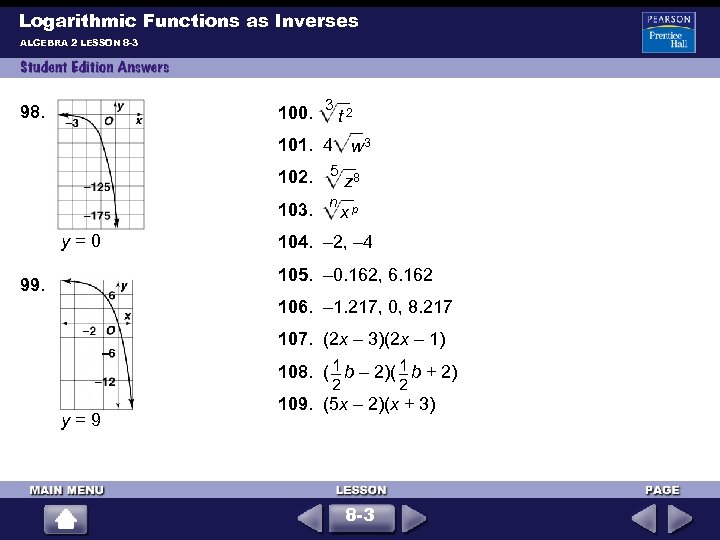
Logarithmic Functions as Inverses ALGEBRA 2 LESSON 8 -3 100. 3 t 2 98. 101. 4 w 3 102. 5 z 8 103. n x p y = 0 104. – 2, – 4 105. – 0. 162, 6. 162 99. 106. – 1. 217, 0, 8. 217 107. (2 x – 3)(2 x – 1) 1 1 108. ( b – 2)( b + 2) 2 y = 9 2 109. (5 x – 2)(x + 3) 8 -3

Logarithmic Functions as Inverses ALGEBRA 2 LESSON 8 -3 Evaluate each logarithm. 1. log 232 5 2. log 10(– 100) undefined 1 3. log 5 25 – 2 Write each equation in exponential form. 4. log 0. 01 = – 2 10– 2 = 0. 01 5. log 327 = 3 33 = 27 6. Graph y = log 6(x – 3) + 1. 8 -3
Properties of Logarithms ALGEBRA 2 LESSON 8 -4 (For help, go to Lessons 8 -3 and 1 -2. ) Simplify each expression. 1. log 24 + log 28 2. log 39 – log 327 3. log 216 ÷ log 264 Evaluate each expression for x = 3. 4. x 3 – x 5 • x 2 6. 8 -4 x 6 x 9 7. x 3 + x 2

Properties of Logarithms ALGEBRA 2 LESSON 8 -4 Solutions 4. x 3 – x for x = 3: 33 – 3 = 27 – 3 = 24 1. log 24 = x log 28 = y 2 x = 4 2 y = 8 x = 2 y = 3 5. x 5 • x 2 for x = 3: 35 • 32 = 3(5+2) = 37 = 2187 log 24 + log 28 = 2 + 3 = 5 2. log 39 = x log 327 = y 3 x = 9 3 y = 27 x = 2 y = 3 x 6 36 6. for x = 3: = 3(6– 9) = 3– 3 = x 9 99 1 = 1 33 27 log 39 – log 327 = 2 – 3 = – 1 7. x 3 + x 2 for x = 3: 33 + 32 = 27 + 9 = 36 3. log 216 = x log 264 = y 2 x = 16 2 y = 64 x = 4 y = 6 4 2 log 216 ÷ log 264 = 4 ÷ 6 = = 3 6 8 -4

Properties of Logarithms ALGEBRA 2 LESSON 8 -4 State the property or properties used to rewrite each expression. a. log 6 = log 2 + log 3 Product Property: log 6 = log (2 • 3) = log 2 + log 3 x 2 b. logb = 2 logb x – logb y y x 2 Quotient Property: logb = logb x 2 – logb y y Power Property: logb x 2 – logb y = 2 logb x – logb y 8 -4

Properties of Logarithms ALGEBRA 2 LESSON 8 -4 Write each logarithmic expression as a single logarithm. a. log 4 64 – log 4 16 = log 4 64 Quotient Property 16 = log 4 4 or 1 Simplify. b. 6 log 5 x + log 5 y = log 5 x 6 + log 5 y = log 5 (x 6 y) Power Property Product Property So log 4 64 – log 4 16 = log 4 4, and 6 log 5 x + log 2 y = log 5 (x 6 y). 8 -4

Properties of Logarithms ALGEBRA 2 LESSON 8 -4 Expand each logarithm. t u a. log 7 t u log 7 = log 7 t – log 7 u Quotient Property b. log(4 p 3) = log 4 + log p 3 Product Property = log 4 + 3 log p Power Property 8 -4

Properties of Logarithms ALGEBRA 2 LESSON 8 -4 Manufacturers of a vacuum cleaner want to reduce its sound intensity to 40% of the original intensity. By how many decibels would the loudness be reduced? Relate: The reduced intensity is 40% of the present intensity. Define: Let l 1 = present intensity. Let l 2 = reduced intensity. Let L 1 = present loudness. Let L 2 = reduced loudness. Write: l 2 = 0. 04 l 1 L 1 = 10 log l 1 l 0 L 2 = 10 log l 2 l 0 8 -4
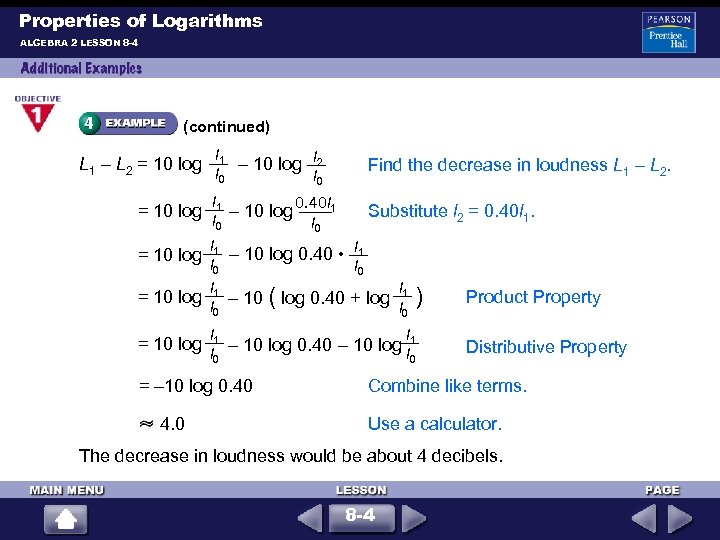
Properties of Logarithms ALGEBRA 2 LESSON 8 -4 (continued) L 1 – L 2 = 10 log l 1 – 10 log l 2 l 0 Find the decrease in loudness L 1 – L 2. l 1 – 10 log 0. 40 l 1 l 0 Substitute l 2 = 0. 40 l 1. l 1 – 10 log 0. 40 • l 1 l 0 l l 1 = 10 log 1 – 10 ( log 0. 40 + log ) l 0 = 10 log l l 1 – 10 log 0. 40 – 10 log l 1 l 0 0 = – 10 log 0. 40 4. 0 Product Property Distributive Property Combine like terms. Use a calculator. The decrease in loudness would be about 4 decibels. 8 -4

Properties of Logarithms ALGEBRA 2 LESSON 8 -4 pages 449– 451 Exercises 1. Product Property 2. Quotient Property 3. Power Property 4. Power Property 5. Power Property, Quotient Property 6. Power Property 7. Power Property, Quotient Property 8. Power Property, Product Property 9. Power Property, Quotient Property 10. Power Property, Product Property 11. log 14 12. log 2 3 13. log 972 14. log 2 20. log 7 22 + log 7 x + log 7 y + log 7 z 17. log 6 5 x 1 1 1 27. log 2 + log x – log y 3 4 15. log m n 16. log 5 2 k 18. log 7 xy z 19. 3 log x + 5 log y 8 -4 21. 22. 23. 24. 25. 26. 1 log 4 5 + log 4 x 2 log 3 + 4 log m – 2 log n log 5 r – log 5 s 2 log 3 2 + 2 log 3 x log 3 7 + 2 log (2 x – 3) 2 log a + 3 log b – 4 log c 2 2 2 1 5 28. 1 + log 8 3 + log 8 a 2 2 1 2 29. log s + log 7 – 2 log t

Properties of Logarithms ALGEBRA 2 LESSON 8 -4 30. –logb x 31. 9 d. B 32. 13 d. B 33. – 2 34. 1 1 42. The coefficient is missing in log 4 s; 51. – 1. 398 43. Answers may vary. Sample: log 150 = log 15 + log 10 55. 0. 3495 2 t 1 log 4 = (log 4 t – log 4 s) 52. 1. 398 s 2 53. – 0. 7782 1 1 = log 4 t – log 4 s. 2 2 54. 1. 5564 35. 6 44. 1. 3803 36. 2 45. 1. 4772 37. 2 38. 1 39. 1 40. – 2 41. 1 56. 12 d. B 57. 0. 00001 58. True; log 2 4 = 2 and 46. 1. 2042 log 2 8 = 3. 47. 2. 097 1 59. False; log 3 3 = 2 48. 0. 1761 1 2 3 log 3 3 , not log 3 . 49. – 0. 0969 50. – 0. 6021 8 -4 2

Properties of Logarithms ALGEBRA 2 LESSON 8 -4 60. True; it is an example of 65. False; log 4 7 – log 4 3 = 71. No; the expression 7 the Power Property since log 4 , not log 4 4. (2 x + 1) is a sum, so 3. 3 8 = 2 it is not covered by 66. True; log x + log (x 2 + 2) the Product, 61. False; the two logs have = log x(x 2 + 2), which Quotient, or Power different bases. equals log (x 3 + 2 x). properties. 62. False; this is not an 67. False; the three logs example of the Quotient have different bases. 72. The log of a product Property. is equal to the sum 68. True; the power and log (x – 2) log x – log 2. = / of the logs. log (MN) quotient properties are = log M + log N. So x 63. False; logb = logb x – used correctly. y log (5 • 2) = log 10 logb y. = 1, log 5 • log 2 69. True; the left side equals 64. False; the exponent on the (0. 7)(0. 3) = 0. 21, 1 logb ( • 43), which left means the log x, 8 which is not equals logb 8. quantity squared, not the equal to 1. 2. log of x 70. 102 d. B 8 -4

Properties of Logarithms ALGEBRA 2 LESSON 8 -4 1 73. log 3 4 2 x 81. log 2 + log 4 + 2 74. logx 2 y z 3 75. log 27 2 1 y mxn 76. log 4 p log r – log s 2 77. logb 3 1 1 2 2 logb z 5 4 x 2 y 3 z 5 4 78. log 2 3 82. logb x + logb y – z 4 3 x 5 3 79. 3 log 2 + log x – 3 log 5 2 80. 3 log m – 4 log n + 2 log p 2 log 4 z – 4 log 4 w 1 2 84. log (x 2 – 4) – 2 log (x + 3) 1 2 1 4 85. log x + log 2 – log y 8 -4 1 87. 2 log 7 (r + 9) – 1 2 log 7 s – log 7 t 3 7 5 83. log 4 x + log 4 y – 2 86. log 3 x + log 3 y – 6 log 3 z 88. v = logb N bv = N MN = bu • bv = bu+v logb MN = u + v logb MN = logb M + logb N

Properties of Logarithms ALGEBRA 2 LESSON 8 -4 90. 89. 1. u = logb M (given) 2. bu = M (Rewrite in exponential form. ) 3. (bu)x = Mx (Raise each side to x power. ) 4. bux = Mx (Power Property of exponents) 5. logb bux = logb Mx (Take the log of each side. ) 6. ux = logb Mx (Simplify. ) 7. logb Mx = x • logb M (substitution) 1. u = logb M (given) 2. bu = M (Rewrite in exponential form. ) 3. v = logb N (given) 4. bv = N (Rewrite in exponential form. ) bu M 5. = = bu–v bv N (Quotient Property of Exponents) M 6. logb = logb bu–v N (Take the log of each side. ) M 7. logb = u – v N (Simplify. ) M 8. logb = logb M – N logb N (substitution) 8 -4 91. B 92. G 93. D 94. [2] By the Quotient 1 Property, log 5 = 2 10 log 5 1. 4307 – 20 1. 8614 = – 0. 4307. [1] correct answer, without work shown
![Properties of Logarithms ALGEBRA 2 LESSON 8 -4 24 95. [4] 1) log = Properties of Logarithms ALGEBRA 2 LESSON 8 -4 24 95. [4] 1) log =](https://present5.com/presentation/25d887b5f81390192d717547acea50df/image-61.jpg)
Properties of Logarithms ALGEBRA 2 LESSON 8 -4 24 95. [4] 1) log = log 24 – 2 log 2; Quotient Property 2) log 2 • 6 = log 2 + log 6; Product Property [2] log 12 written two ways OR written 4 ways but properties not named 1 2 3) log 144 = 1 log 144; Power 2 Property 4) log 3 • 22 = log 3 + 2 log 2; Product and Power Properties [3] log 12 written three ways 96. 97. 98. 99. 101. 64 7 102. 2 103. – [1] log 12 written only 2 ways and properties 104. not named 105. log 7 49 = 2 106. 3 = log 5 125 107. 1 2 log 8 = – 4 3 108. 1 – 3 = log 5 125 100. 8, – 8 8 -4 3, 5 i, – 4 i – 2 i, – 4 – i – 2, – i – 1 7, 11 2 i + 3, –i

Properties of Logarithms ALGEBRA 2 LESSON 8 -4 Write each expression as a single logarithm. State the property you used. 1. log 12 – log 3 2. 3 log 115 + log 117 log 4; Quotient Property log 11(53 • 7); Power Property and Product Property Expand each logarithm. 3. logc a 4. log 3 x 4 b 4 log 3 x logca – logcb Use the properties of logarithms to evaluate each expression. 1 6. logyy 5. log 0. 001 + log 100 2 1 2 – 1 8 -4
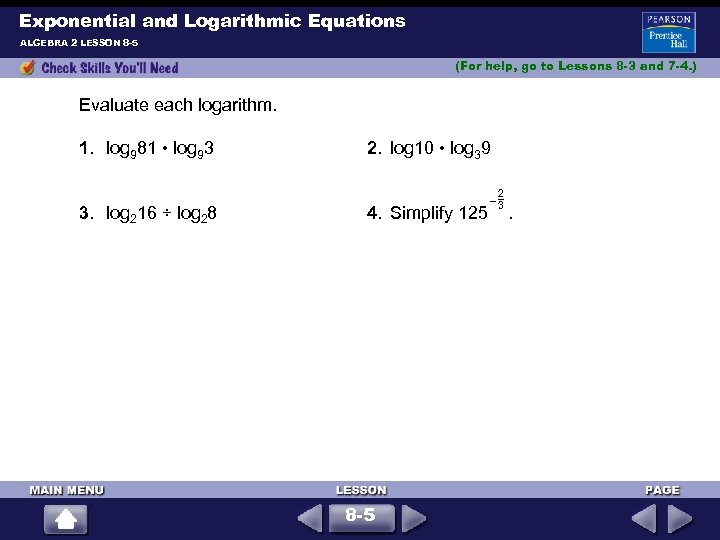
Exponential and Logarithmic Equations ALGEBRA 2 LESSON 8 -5 (For help, go to Lessons 8 -3 and 7 -4. ) Evaluate each logarithm. 1. log 981 • log 93 3. log 216 ÷ log 28 2. log 10 • log 39 – 2 3 4. Simplify 125 . 8 -5

Exponential and Logarithmic Equations ALGEBRA 2 LESSON 8 -5 Solutions 2. log 10 = x log 39 = y 10 x = 10 3 y = 9 x = 1 y = 2 1. log 981 = x log 93 = y 9 x = 81 9 y = 3 x = 2 y = 1 2 1 log 981 • log 93 = 2 • = 1 2 log 10 • log 39 = 1 • 2 = 2 3. log 216 = x log 28 = y 2 x = 16 2 y = 8 x = 4 y = 3 4 log 216 ÷ log 28 = 4 ÷ 3 = or 1 1 3 – 2 3 1 4. 125 = 2 3 125 = 1 1 2 3 (125 ) 3 1 1 = 3 = = ( ) 52 25 1 2 8 -5
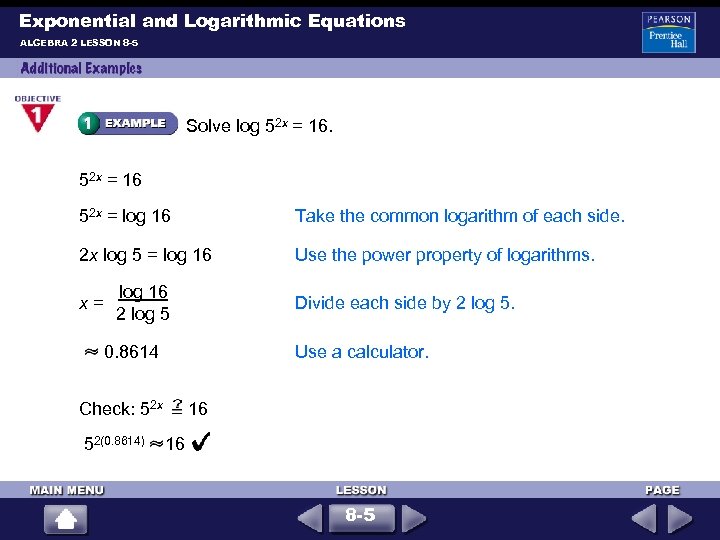
Exponential and Logarithmic Equations ALGEBRA 2 LESSON 8 -5 Solve log 52 x = 16 52 x = log 16 Take the common logarithm of each side. 2 x log 5 = log 16 Use the power property of logarithms. x = log 16 2 log 5 0. 8614 Divide each side by 2 log 5. Use a calculator. Check: 52 x 16 52(0. 8614) 16 8 -5
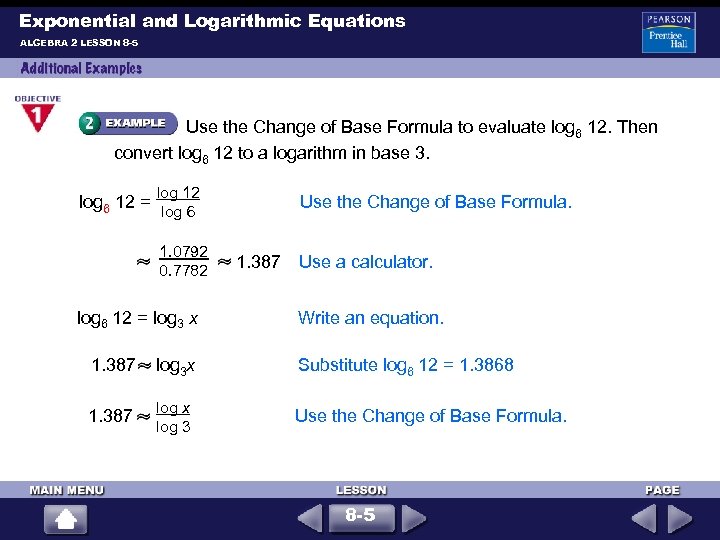
Exponential and Logarithmic Equations ALGEBRA 2 LESSON 8 -5 Use the Change of Base Formula to evaluate log 6 12. Then convert log 6 12 to a logarithm in base 3. log 12 log 6 12 = log 6 1. 0792 0. 7782 log 6 12 = log 3 x 1. 387 log 3 x 1. 387 log x log 3 Use the Change of Base Formula. 1. 387 Use a calculator. Write an equation. Substitute log 6 12 = 1. 3868 Use the Change of Base Formula. 8 -5
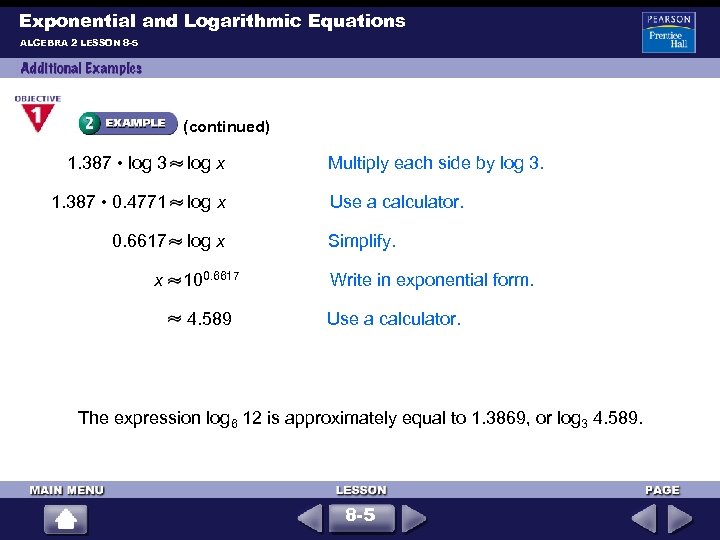
Exponential and Logarithmic Equations ALGEBRA 2 LESSON 8 -5 (continued) 1. 387 • log 3 log x 1. 387 • 0. 4771 log x 0. 6617 log x x 100. 6617 4. 589 Multiply each side by log 3. Use a calculator. Simplify. Write in exponential form. Use a calculator. The expression log 6 12 is approximately equal to 1. 3869, or log 3 4. 589. 8 -5
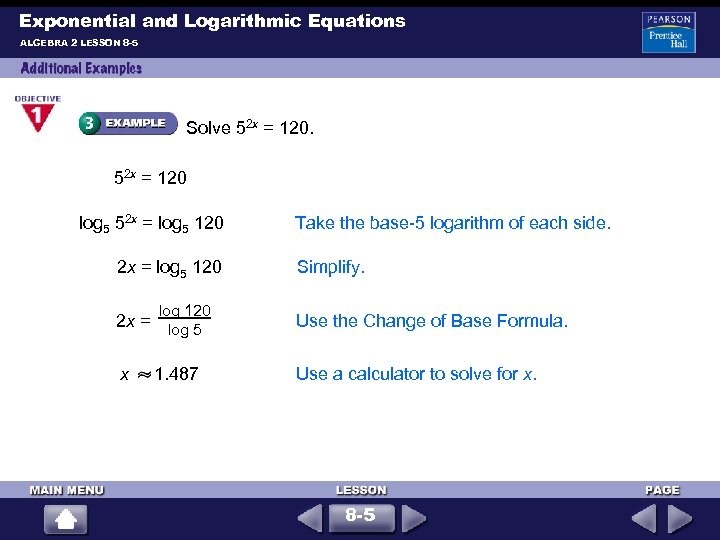
Exponential and Logarithmic Equations ALGEBRA 2 LESSON 8 -5 Solve 52 x = 120 log 5 52 x = log 5 120 log 120 Take the base-5 logarithm of each side. Simplify. 2 x = log 5 Use the Change of Base Formula. x 1. 487 Use a calculator to solve for x. 8 -5
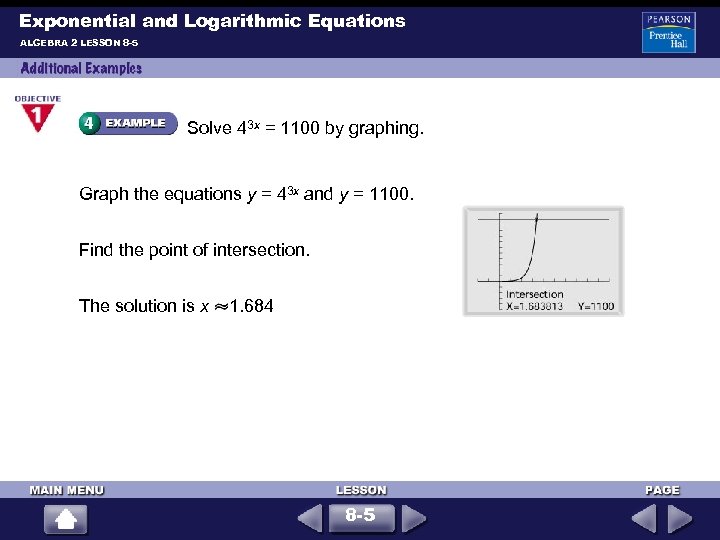
Exponential and Logarithmic Equations ALGEBRA 2 LESSON 8 -5 Solve 43 x = 1100 by graphing. Graph the equations y = 43 x and y = 1100. Find the point of intersection. The solution is x 1. 684 8 -5
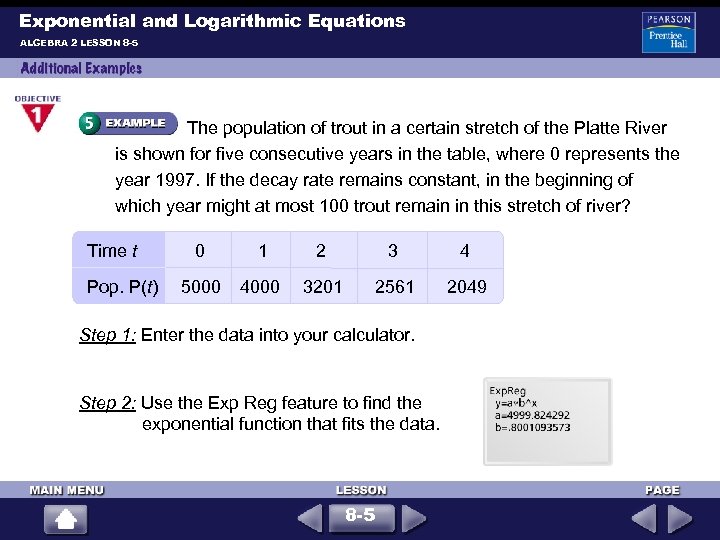
Exponential and Logarithmic Equations ALGEBRA 2 LESSON 8 -5 The population of trout in a certain stretch of the Platte River is shown for five consecutive years in the table, where 0 represents the year 1997. If the decay rate remains constant, in the beginning of which year might at most 100 trout remain in this stretch of river? Time t Pop. P(t) 0 1 2 3 4 5000 4000 3201 2561 2049 Step 1: Enter the data into your calculator. Step 2: Use the Exp Reg feature to find the exponential function that fits the data. 8 -5
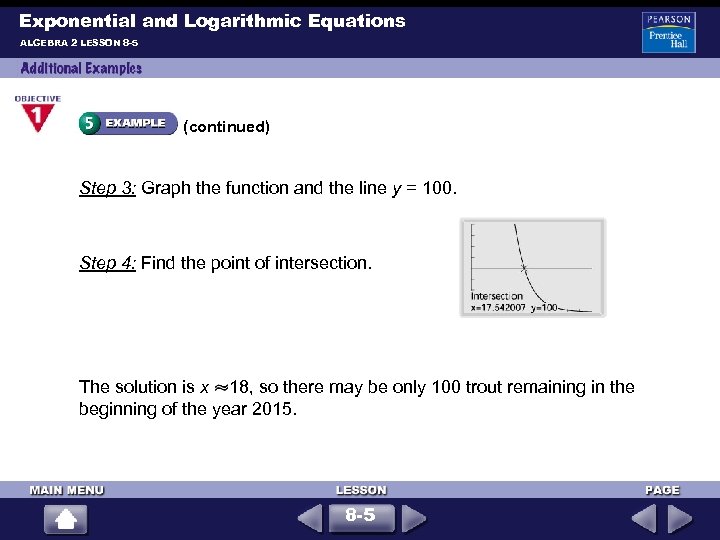
Exponential and Logarithmic Equations ALGEBRA 2 LESSON 8 -5 (continued) Step 3: Graph the function and the line y = 100. Step 4: Find the point of intersection. The solution is x 18, so there may be only 100 trout remaining in the beginning of the year 2015. 8 -5
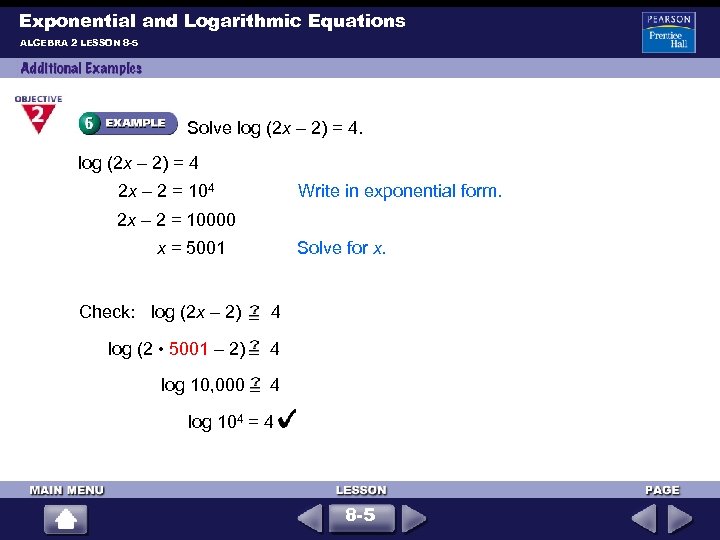
Exponential and Logarithmic Equations ALGEBRA 2 LESSON 8 -5 Solve log (2 x – 2) = 4 2 x – 2 = 104 Write in exponential form. 2 x – 2 = 10000 x = 5001 Solve for x. Check: log (2 x – 2) 4 log (2 • 5001 – 2) 4 log 10, 000 4 log 104 = 4 8 -5
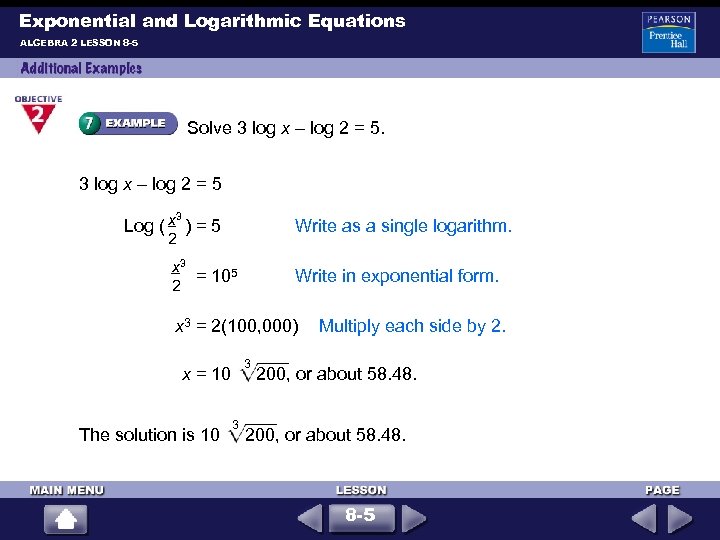
Exponential and Logarithmic Equations ALGEBRA 2 LESSON 8 -5 Solve 3 log x – log 2 = 5 x Log ( ) = 5 3 Write as a single logarithm. 2 x 3 = 105 2 Write in exponential form. x 3 = 2(100, 000) Multiply each side by 2. 3 x = 10 200, or about 58. 48. 3 The solution is 10 200, or about 58. 48. 8 -5
Exponential and Logarithmic Equations ALGEBRA 2 LESSON 8 -5 pages 456– 460 Exercises 10. 0. 2720 19. 2. 3219 11. 3. 1699; log 8 729 20. 0. 8496 12. 1. 5; log 8 22. 627 21. 0. 0499 13. 3. 6309; log 8 1901. 3 22. 3. 0101 14. 2. 5643; log 8 206. 93 23. 1. 0219 15. 3. 1827; log 8 748. 56 24. 0. 9746 7. 0. 9534 16. 2. 8074; log 8 343 25. 0. 2009 8. 0. 3579 17. 3. 8737; log 8 3149. 6 26. 5. 2379 9. 3. 2056 18. 0. 0792; log 8 1. 1790 1. 1. 5850 2. 2. 1240 3. 2. 7320 4. 3. 0101 5. 3 6. 3. 4650 8 -5

Exponential and Logarithmic Equations ALGEBRA 2 LESSON 8 -5 27. 0. 5690 35. 33 28. 1. 2871 36. 10, 000 29. 4. 7027 1 37. 60 , or 0. 0167 30. 14. 4894 43. 100, 000 5, or 223, 606. 8 38. 12 44. 5 1 45. 4 46. 1357. 2 31. about 7. 1 years 39. 10, or 3. 1623 47. 7 32. about 2018 40. 100 10 – 1, or 315. 2 33. 0. 05 41. 2 10 34. 10 , or 0. 3162 42. 3 108 8 -5

Exponential and Logarithmic Equations ALGEBRA 2 LESSON 8 -5 x 1 51. 2 = 10( )1. 17 , 2. 7 min 2 48. a. 18. 9658 b. 18. 9658 52. c. Answers may vary. Sample: You don’t 53. have to use the Change of Base 54. formula with the base 10 method, but there is 55. less algebra with the base-2 method. 56. 75 = 125(0. 88)x, 4 years 3 1 2 3 2 b. 2011 1 57. 3 50. 20 = 8(1. 2)x, 5 years 60. – 1 61. a. Florida growth factor = 1. 0213, y = 15, 982, 378 • (1. 0213)x; New York growth factor = 1. 0054, y = 18, 976, 457 • (1. 0054)x – 1 49. 5. 1 59. 3 58. – 2 8 -5

Exponential and Logarithmic Equations ALGEBRA 2 LESSON 8 -5 62. a. Texas growth factor 63. Since Florida’s growth 65. Answers may vary. = 1. 0208, y = rate is larger than Sample: log x = 1. 6 20, 851, 820 Texas’s growth rate, in 101. 6 = x, x 39. 81 (1. 0208)x; California theory, given constant growth factor = conditions, Florida 66. Answers may vary. 1. 013, y = would exceed Texas in Sample: A possible 33, 871, 648 • about 543 years. model is y = (1. 013)x However, since no 1465(1. 0838)x where x state has unlimited = 0 represents 1991; b. 2063 capacity for growth, it is the growth is probably unrealistic to predict exponential and over a long period of 1465(1. 0838)10 3276; time. using this model, there will be 10, 000 log 102 64. 2 – 1 manatees in about = / log 101 2015. 8 -5

Exponential and Logarithmic Equations ALGEBRA 2 LESSON 8 -5 67. a. x = log b log a b. x = logab = 68. log 2 log b log a c. Substituting the result from part (a) into the results from part (b), or vice versa, yields log b logab = . This log a justifies the Change of Base Formula for log 7 69. log 8 log 3 70. log 140 log 5 71. log 3. 3 log 9 72. log 3 x log 4 73. log (1 – x) 76. a. 100 (or 1) W/m 2, 104 W/m 2 b. 10, 000 times more intense 77. a. top up: 10– 5 W/m 2, top down: 10– 2. 5 W/m 2 b. 99. 68% 74. log 5 78. a. 10– 3 W/m 2, 106 W/m 2 b. 109 times more intense 75. log (x + 1) 79. 2. 9315 log 6 log x c = 10. 8 -5

Exponential and Logarithmic Equations ALGEBRA 2 LESSON 8 -5 80. 0. 2098 89. 2. 9615 81. 0. 6225 90. 2. 7944 82. 625 91. 1 83. 2. 3094 92. 500 97. a. bassoon, guitar, harp, violin, viola, cello b. bassoon, guitar, harp, cello, bass c. harp, violin d. harp, violin 84. 10 93. 1. 0451 98. 478, 630 times 85. 0. 8505 94. 114. 3 86. 1. 5 95. 1. 3063 87. 7. 4168 96. 3. 0417 99. no; solving x 0. 65 = for x, the (0. 5)5430 age in years of the sample, yields an age of about 3561 yrs. 88. 200. 8 100. 5 8 -5

Exponential and Logarithmic Equations ALGEBRA 2 LESSON 8 -5 101. – 4, 2 110. 27. 7 102. – 9, 9 111. 249. 5 103. 1 112. 103 104. 20, 031 m above sea level 113. log 2 + 3 log x – 2 log y 114. log 3 x – log 3 y 105. a. 91 hours or 4 days b. 0. 928 mg or 1. 061 mg c. Estimate in hours is more accurate; the days have a larger rounding error. 115. 3 log 2 3 + 3 log 2 x 116. log 3 7 + 2 log 3 (2 x – 3) 1 2 117. log 4 5 + log 4 x 118. log 2 5 + log 2 a – 2 log 2 b 106. 1. 11 119. x 2 + 3 x – 1 107. 7. 30 120. x 2 – 3 x – 1 108. 2. 19 121. 3 x 3 – 3 x 109. 138. 8 122. 1, ±i 8 -5
Exponential and Logarithmic Equations ALGEBRA 2 LESSON 8 -5 123. ± 2, ± 2 i 124. ± 2, ± 3 125. – 2, – 1, 3 126. 2(x) + 2(x + 12) = 128; 26 ft 679 + x 127. = 133; 119 6 8 -5
Exponential and Logarithmic Equations ALGEBRA 2 LESSON 8 -5 Use mental math to solve each equation. 1 1. 2 x = 8 – 3 4. Solve 52 x = 125. 2. log 42 = x 3 2 8 -5 1 2 3. 106 x = 1 0
Natural Logarithms ALGEBRA 2 LESSON 8 -6 (For help, go to Lessons 8 -2 and 8 -5. ) Use your calculator to evaluate each expression to the nearest thousandth. 1. e 5 Solve. 6. log 3 x = 4 2. 2 e 3 1 3. e– 2 4. e 7. log 164 = x 8 -6 5. 4. 2 e 8. log 16 x = 4
Natural Logarithms ALGEBRA 2 LESSON 8 -6 Solutions 1. e 5 148. 413 2. 2 e 3 40. 171 3. e– 2 0. 135 4. 0. 368 e 1 5. 4. 2 e 11. 417 6. log 3 x = 4 7. log 164 = x 8. log 16 x = 4 34 = x 81 = x 16 x = 4 x = 1 164 = x 65, 536 = x 2 8 -6
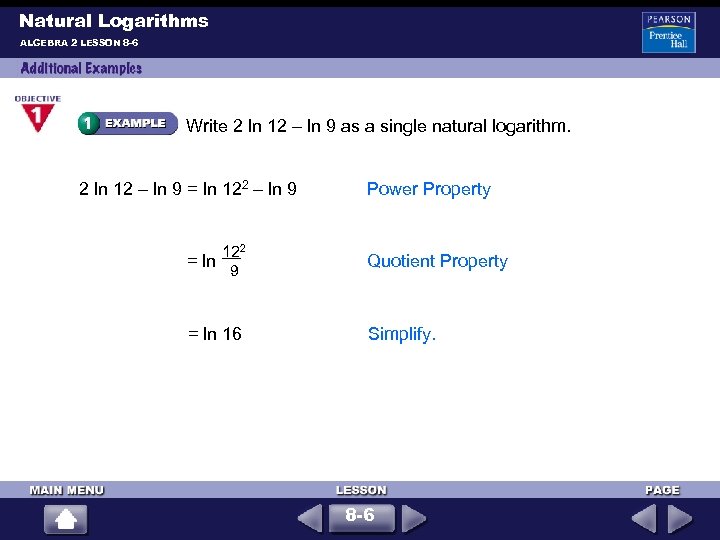
Natural Logarithms ALGEBRA 2 LESSON 8 -6 Write 2 ln 12 – ln 9 as a single natural logarithm. 2 ln 12 – ln 9 = ln 122 9 = ln 16 Power Property Quotient Property Simplify. 8 -6
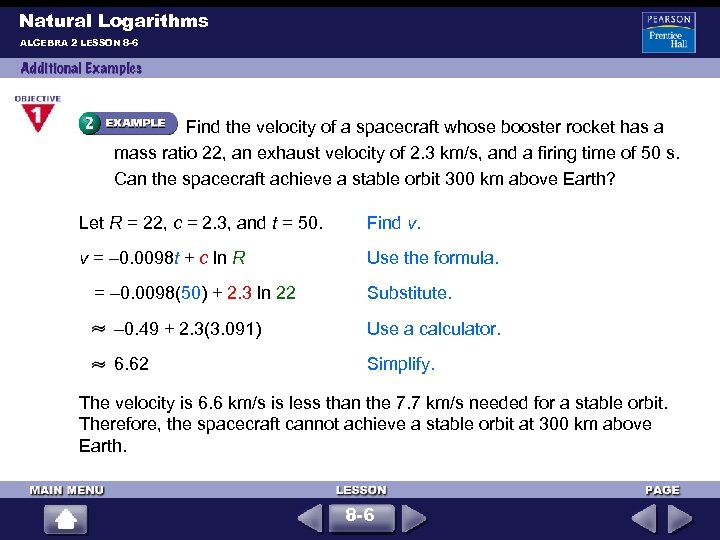
Natural Logarithms ALGEBRA 2 LESSON 8 -6 Find the velocity of a spacecraft whose booster rocket has a mass ratio 22, an exhaust velocity of 2. 3 km/s, and a firing time of 50 s. Can the spacecraft achieve a stable orbit 300 km above Earth? Let R = 22, c = 2. 3, and t = 50. Find v. v = – 0. 0098 t + c ln R Use the formula. = – 0. 0098(50) + 2. 3 ln 22 Substitute. – 0. 49 + 2. 3(3. 091) Use a calculator. 6. 62 Simplify. The velocity is 6. 6 km/s is less than the 7. 7 km/s needed for a stable orbit. Therefore, the spacecraft cannot achieve a stable orbit at 300 km above Earth. 8 -6
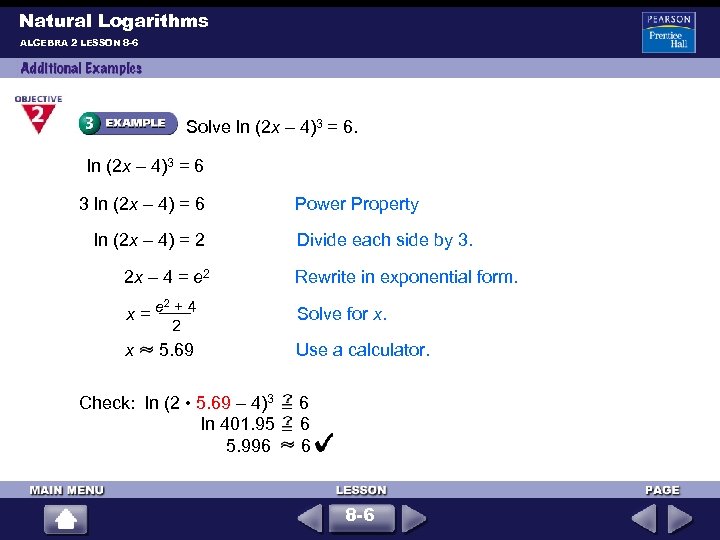
Natural Logarithms ALGEBRA 2 LESSON 8 -6 Solve ln (2 x – 4)3 = 6 3 ln (2 x – 4) = 6 ln (2 x – 4) = 2 Power Property Divide each side by 3. 2 x – 4 = e 2 Rewrite in exponential form. 2 x = e + 4 Solve for x. x 5. 69 Use a calculator. 2 Check: ln (2 • 5. 69 – 4)3 6 ln 401. 95 6 5. 996 6 8 -6
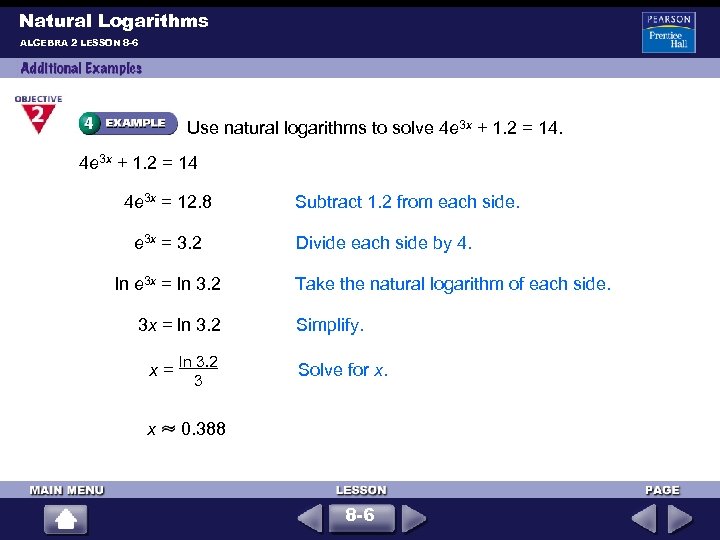
Natural Logarithms ALGEBRA 2 LESSON 8 -6 Use natural logarithms to solve 4 e 3 x + 1. 2 = 14 4 e 3 x = 12. 8 e 3 x = 3. 2 ln e 3 x = ln 3. 2 x = ln 3. 2 3 Subtract 1. 2 from each side. Divide each side by 4. Take the natural logarithm of each side. Simplify. Solve for x. x 0. 388 8 -6
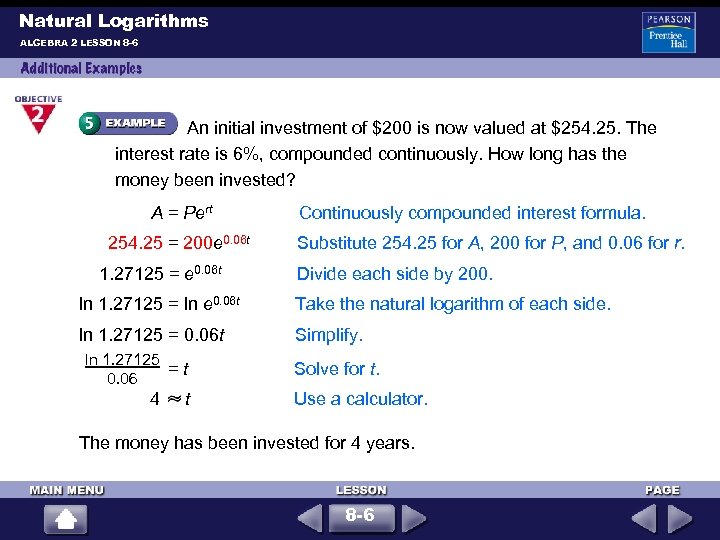
Natural Logarithms ALGEBRA 2 LESSON 8 -6 An initial investment of $200 is now valued at $254. 25. The interest rate is 6%, compounded continuously. How long has the money been invested? A = Pert 254. 25 = 200 e 0. 06 t 1. 27125 = e 0. 06 t Continuously compounded interest formula. Substitute 254. 25 for A, 200 for P, and 0. 06 for r. Divide each side by 200. ln 1. 27125 = ln e 0. 06 t Take the natural logarithm of each side. ln 1. 27125 = 0. 06 t Simplify. ln 1. 27125 = t 0. 06 4 t Solve for t. Use a calculator. The money has been invested for 4 years. 8 -6

Natural Logarithms ALGEBRA 2 LESSON 8 -6 pages 464– 467 Exercises 11. 24. 13 23. 2. 890 1. In 125 12. 7. 79 km/s; yes 24. 1. 151 2. In 18 13. 25 seconds 25. 2. 401 3. In 4 14. 134. 476 26. 5. 493 4. In 40, 960 15. 0. 135 27. 1. 242 16. 1. 078 1015 28. 23. 752 1 5. In 81 6. In 1 m 5 7. In 3 8. In 9. In xy z 4 a c b 2 10. 20. 92 17. 1488. 979 18. 5. 482, – 3. 482 19. ± 11. 588 20. 110. 196 21. ± 2. 241 22. ± 0. 908 8 -6 29. 6 years 30. 78% 31. 1 32. 2 33. 10 34. 10

Natural Logarithms ALGEBRA 2 LESSON 8 -6 35. 0 47. 3. 6 59. 1. 2639 36. 1 48. 6. 7 60. no solution 37. 1 49. 9. 4 61. 27, 347. 9 38. 83 50. 11. 8 62. 78. 342 39. 10. 8 51. 13. 9 40. 301 days; 26 days 52. 15. 8 41. sometimes 53. 17. 5 42. never 54. 19. 1 43. always 55. 542. 31 44. about 5. 8% per hour 56. 1 63. No; using the Change of Base Formula would result in one of the log expressions being written as a quotient of logs, which couldn’t then be combined with the other expression to form a single logarithm. 45. 19. 8 hours 57. 0. 0794 46. about 40, 000 bacteria 58. 81. 286 4 8 -6
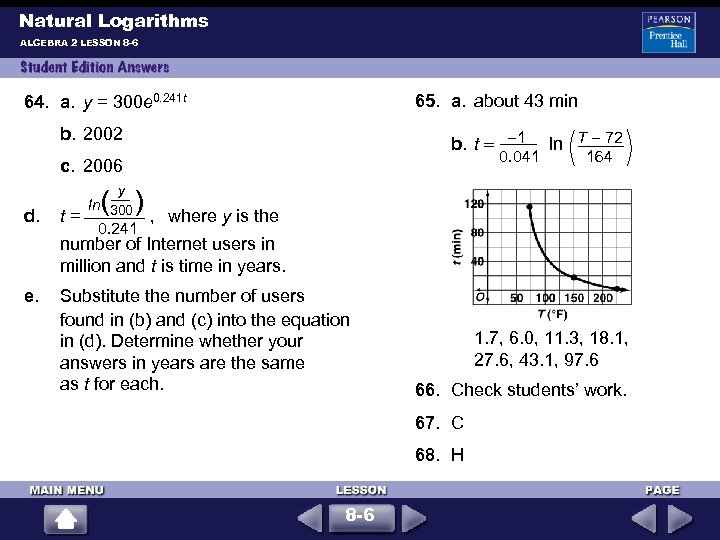
Natural Logarithms ALGEBRA 2 LESSON 8 -6 65. a. about 43 min 64. a. y = 300 e 0. 241 t b. 2002 1 b. t ln T 72 0. 041 c. 2006 d. 164 y ln 300 ( ) t = , where y is the 0. 241 number of Internet users in million and t is time in years. e. Substitute the number of users found in (b) and (c) into the equation in (d). Determine whether your answers in years are the same as t for each. 1. 7, 6. 0, 11. 3, 18. 1, 27. 6, 43. 1, 97. 6 66. Check students’ work. 67. C 68. H 8 -6
![Natural Logarithms ALGEBRA 2 LESSON 8 -6 69. B 71. 4 70. [4] a. Natural Logarithms ALGEBRA 2 LESSON 8 -6 69. B 71. 4 70. [4] a.](https://present5.com/presentation/25d887b5f81390192d717547acea50df/image-93.jpg)
Natural Logarithms ALGEBRA 2 LESSON 8 -6 69. B 71. 4 70. [4] a. 8% 72. 2. 846 b. A = Pert = 500 e 0. 08 t c. 1800 = 500 e 0. 08 t 3. 6 = e 0. 08 t ln 3. 6 = 0. 08 t 73. 0. 272 74. 3333. 3 75. 1. 002 76. 9. 0 10– 5 ln 3. 6 = t 0. 08 x – 7 77. y = ; yes 5 16 t about 16 years 3 x – 10 78. y = ; yes 2 [3] correct model computation error in (b) or (c) [2] incorrect model, solved correctly [1] correct model, but without work shown in (c) 8 -6 79. y = ± 5 – x ; no 80. 4060 possible combinations
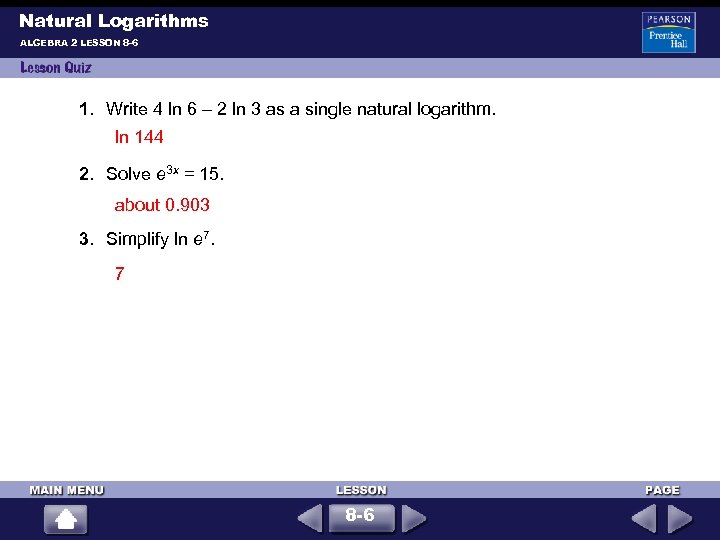
Natural Logarithms ALGEBRA 2 LESSON 8 -6 1. Write 4 ln 6 – 2 ln 3 as a single natural logarithm. ln 144 2. Solve e 3 x = 15. about 0. 903 3. Simplify ln e 7. 7 8 -6
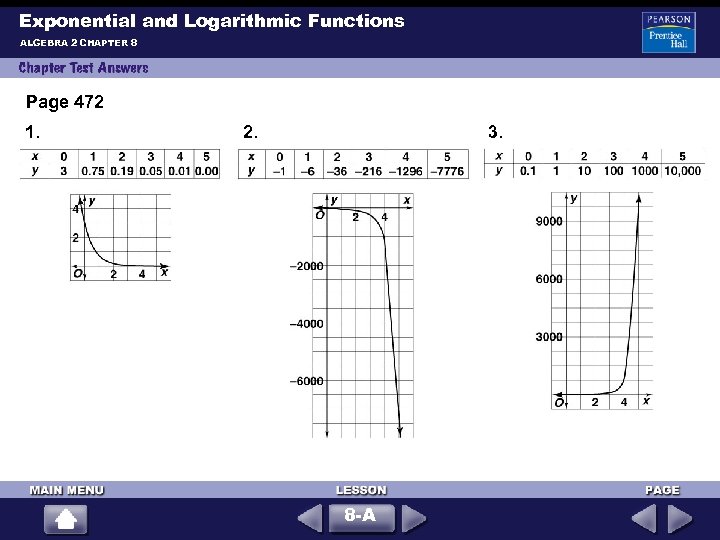
Exponential and Logarithmic Functions ALGEBRA 2 CHAPTER 8 Page 472 1. 2. 3. 8 -A

Exponential and Logarithmic Functions ALGEBRA 2 CHAPTER 8 4. 5. Answers may vary. Both 12. y = 5 x translated right answers should be of the 2 units and down 1 form y = abx. For the unit growth model, 13. y = 2 x translated left b > 1. For the decay 2 units and reflected model, 0 < b < 1. over the x-axis 1 6. y = (3)x 14. 3 3 7. y = 2(5)x 15. 1 8. y = 4(4)x 16. 2 9. 4. 11 years 17. 3 10. y = 3 x translated up 2 units 18. 0 1 11. y = 3( )x translated left 1 2 unit 8 -A 19. 4

Exponential and Logarithmic Functions ALGEBRA 2 CHAPTER 8 20. 24. log 2 2916 32. Answers may vary. Sample: 25. log a 2 Taking common logarithms of both sides gives 2 x = 26. log 7 a – log 7 b . Taking logarithms to the log 3 base 3 of both sides gives 2 x = log 3 4, which by the Change of Base Formula is equivalent to 2 x = . log 4 – 15. 28 log 3 3. 89 250 0. 01 3 b 21. log 4 27. log 3 + 3 log x + 2 log y 22. 28. 1 33. 34. 35. 36. 29. 13 23. 30. – 1 31. 3 8 -A

Exponential and Logarithmic Functions ALGEBRA 2 CHAPTER 8 log 16 log 3 1 38. log 2 39. log 8 log 7 37. 40. 1. 359 41. 7. 456 42. 17. 058, – 16. 058 43. 4. 780 44. 99 cm 8 -A
25d887b5f81390192d717547acea50df.ppt