Exploring Exponential Growth and Decay Activity — Take

Exploring Exponential Growth and Decay Activity - Take out warm-up - Take out a blank piece of paper

Objective – To be able to graph exponential growth and decay functions and to become familiar with asymptotes. State Standard – 12. 0 Students understand exponential functions and use them in problems with exponential growth and decay. Asymptote – is the line that a graph approaches as you move away from the origin.

Exponential Functions – involves the expression y = abx base – is the value b, with the exponent Exponential Growth Exponential Decay If a > 0 and b > 1 If a > 0 and 0 < b < 1 10 y 10 9 8 7 6 5 = 4(3)x 4 3 2 1 – 5 – 4 – 3 – 2 – 1 1 2 3 4 5 9 8 7 6 5 4 3 2 1 – 5 – 4 – 3 – 2 – 1 y = 3(½)x 1 2 3 4 5

Tell me if the equation is Growth, Decay, or Neither. x Decay b) y = -3( 2 ) x Neither c) y = 5( 3/ ) x d) y = 8( 8/ ) x a) y = 4( 1/ 4) 7 3 Decay Growth

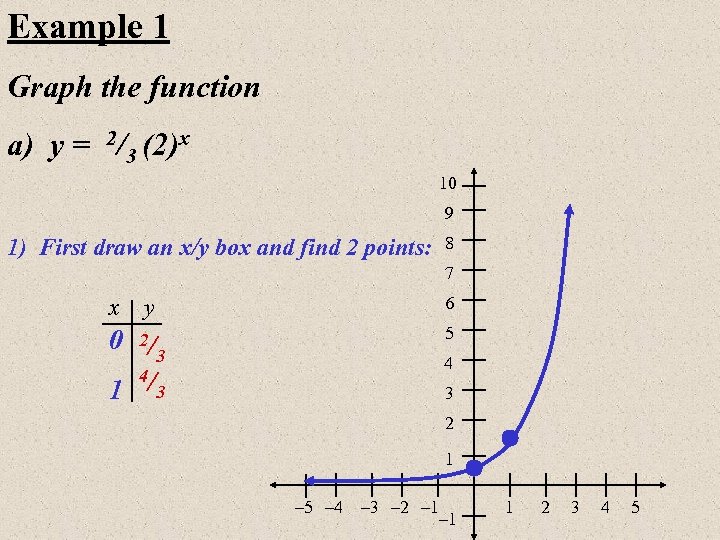Example 1 Graph the function a) y = 2/3 (2)x 10 9 1) First draw an x/y box and find 2 points: 8 7 x y 6 0 2/3 4/ 1 3 5 4 3 2 1 – 5 – 4 – 3 – 2 – 1 1 2 3 4 5

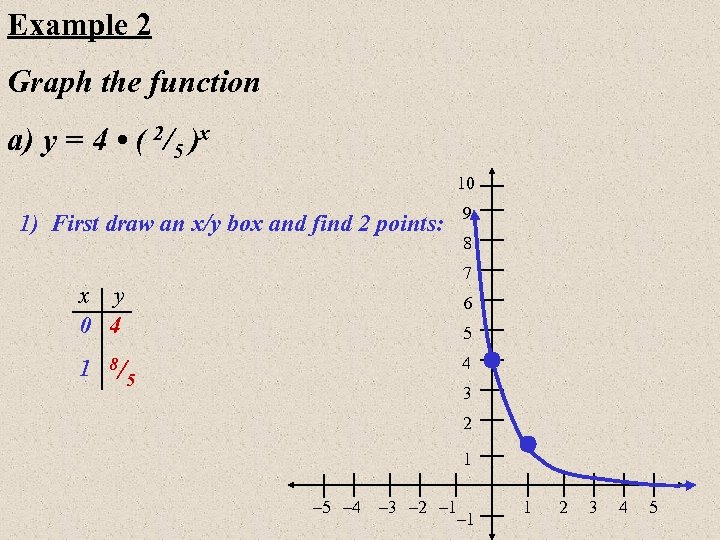Example 2 Graph the function a) y = 4 • ( 2/5 )x 10 1) First draw an x/y box and find 2 points: 8/ 8 7 x y 0 4 1 9 6 5 4 5 3 2 1 – 5 – 4 – 3 – 2 – 1 1 2 3 4 5

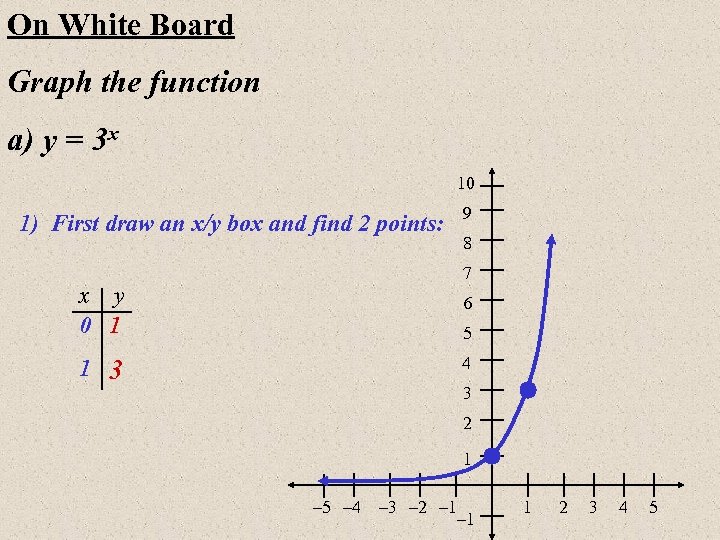On White Board Graph the function a) y = 3 x 10 1) First draw an x/y box and find 2 points: 9 8 7 x y 0 1 6 5 4 1 3 3 2 1 – 5 – 4 – 3 – 2 – 1 1 2 3 4 5

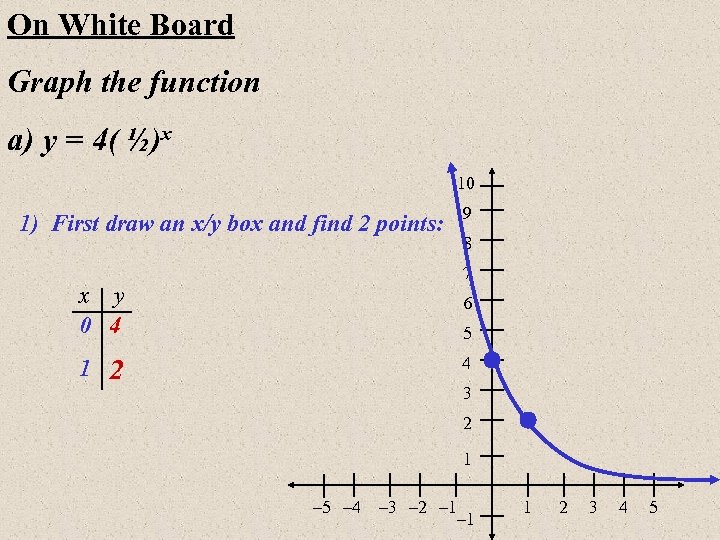On White Board Graph the function a) y = 4( ½)x 10 1) First draw an x/y box and find 2 points: 9 8 7 x y 0 4 6 5 4 1 2 3 2 1 – 5 – 4 – 3 – 2 – 1 1 2 3 4 5

Appreciation/Depreciation Model A = P(1 ± Where A = Final Amount P = Initial Amount r = Percent Rate t = Time (usually in years) t r)

Example 6 You buy a car for $4000 when you are 16 and find out it depreciates by 12 percent each year. How much is your car worth when you want to sell it when you are 20? First Identify your P, r, t, and if we are adding or subtracting. A = 4000 ( 1 – 0. 12)4 A = 4000(0. 5997) A = 4000 (0. 88)4 A = 2398. 78 So you could roughly sell your car for $2400 when you are 20.

Example 7 Now you buy a classic car for $4000 that appreciates in value 12% each year. How much is your car worth when you want to sell it when you are 20 A = 4000 ( 1 + 0. 12)4 A = 4000 (1. 12)4 A = 4000(1. 57352) A = 6294. 08 So you could roughly sell your car for $6300 when you are 20.

See Assignment Sheet

Simplify 1) (1 + ½)2 ( 3/2 )2 9/ 4 2) 3) (1 + 1/4 )4 ( 5/4 )4 625/ 256 2) (1 + 1/3 )3 ( 4/3 )3 64/ 27

Objective – To be able to identify the role of “h” and “k” for exponential growth and decay. And use the “e” as a base. State Standard – 12. 0 Students understand exponential functions and use them in problems with exponential growth and decay.

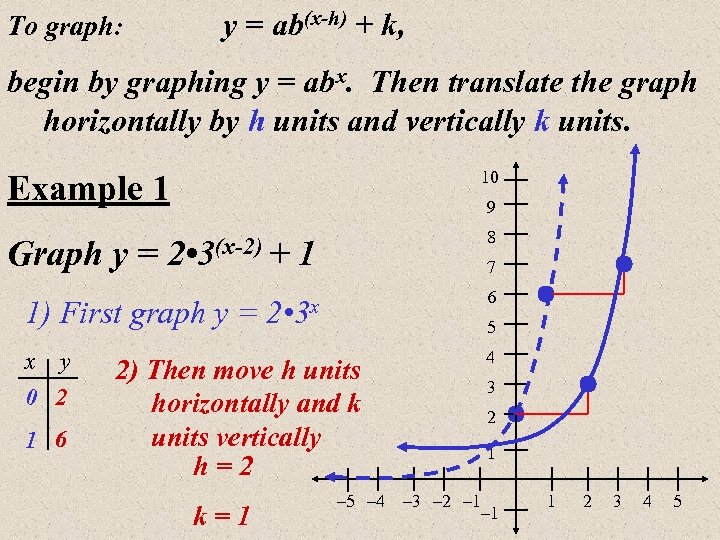y = ab(x-h) + k, To graph: begin by graphing y = abx. Then translate the graph horizontally by h units and vertically k units. 10 Example 1 Graph y = 9 1) First graph y = x y 0 2 1 6 1 8 2 • 3 x 6 2 • 3(x-2) + 7 5 4 2) Then move h units horizontally and k units vertically h=2 k=1 – 5 – 4 3 2 1 – 3 – 2 – 1 1 2 3 4 5

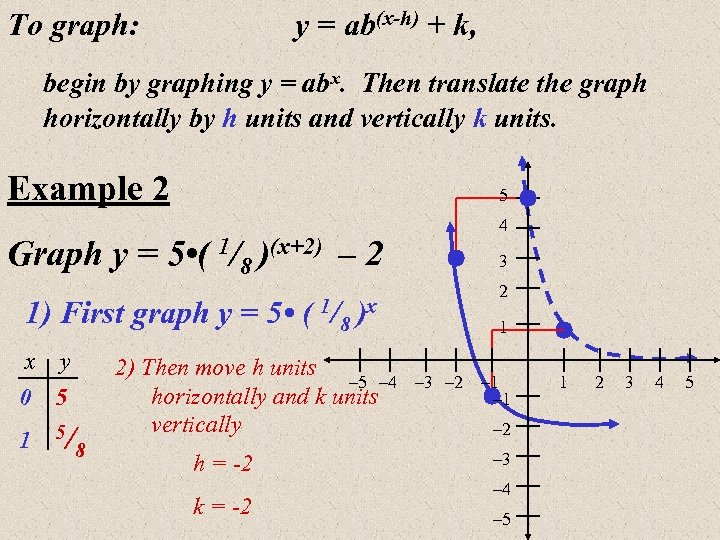To graph: y = ab(x-h) + k, begin by graphing y = abx. Then translate the graph horizontally by h units and vertically k units. Example 2 5 4 Graph y = 5 • ( 1/8 )(x+2) – 2 3 2 1) First graph y = 5 • ( 1/8 )x x y 0 5 1 5/ 2) Then move h units – 5 – 4 horizontally and k units vertically 8 h = -2 k = -2 1 – 3 – 2 – 1 – 2 – 3 – 4 – 5 1 2 3 4 5

THE NATURAL BASE e The natural base e is irrational. It is defined as follows: As n approaches + , (1 + 1/n)n approaches e 2. 71828459

Example 3 Simplify the expression a) e 2 • e 3 2+3 e 5 e b) (20 e 4)/(5 e 3) 4 -3 4 e 1 4 e 4 e c) (4 e-3 x)2 (-3 x)2 16 e (-6 x) 16 e 16 6 x e

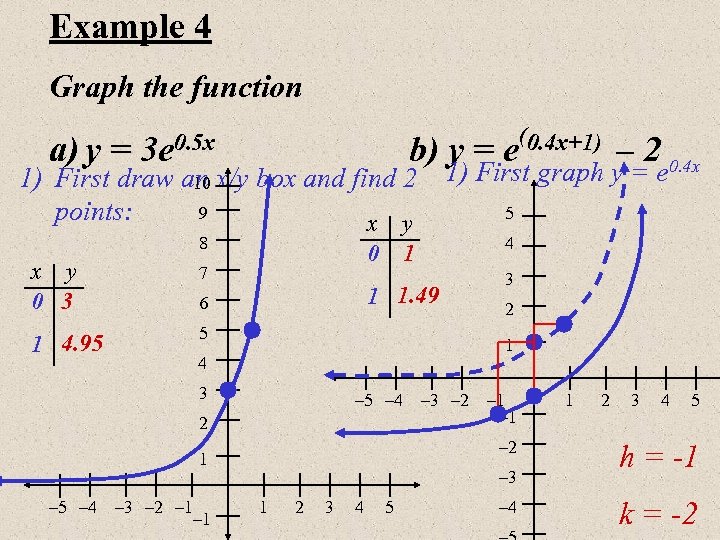Example 4 Graph the function a) y = 3 e 0. 5 x b) y = e x y 0 3 7 1 4. 95 0 5 4 1 5 1 1. 49 6 4 – 5 – 4 2 – 1 2 – 3 – 2 – 1 – 2 1 – 3 – 2 – 1 3 – 5 – 4 – 2 0. 4 x 1) First graph y = e 1) First draw an x/y box and find 2 10 9 points: x y 8 (0. 4 x+1) – 3 1 2 3 4 5 – 4 1 2 3 4 5 h = -1 k = -2

Find the value of x. 1) 3 x = 9 2 2) 3) 100 = x 1 2) x 3 = -8 -2 4) ( 3/2 )-1 = x 2/ 3

http: //www. youtube. com/watch? v=Qbd 0 u. SPG 5 y. Q http: //www. youtube. com/watch? v=4 Y-62 Ti 5_6 s The Richter Scale Magnitude +1 0 1 2 3 E 4 5 6 7 8 9 E(30)2 E(30)3 E(30)4 E(30)5 E(30)6 E(30)7 E(30)8 E(30)9 energy released: x 30

8. 3 Logarithmic Functions Objective – To be able to evaluate and graph logarithmic functions. State Standard – 11. 1 Students solve problems involving logarithms and exponents DEFINITION OF LOGARITHM WITH BASE b logby = x if and only if bx = y The expression logby is read as “log base b of y. ”

Example 1 Rewrite the logarithmic equation in exponential form. a) log 3 9 = 2 32 = 9 b) log 8 1 = 0 80 = 1 c) log 5 (1/25) = -2 5(-2) = 1/25 Example 2 Evaluate the expression. a) log 4 64 4 x = 64 x=3 b) log 3 27 3 x = 27 x=3 c) log 6 ( 1/36 ) 6 x = 1/36 x = -2

Common Logarithm – Is a log with base 10. ie. log 10 or simply just log so…… log 10 x = log x GRAPHS OF LOGARITHMIC FUNCTIONS y = logb (x – h) + k if 0 < b < 1 then the graph moves down, if b > 1 the graph moves up

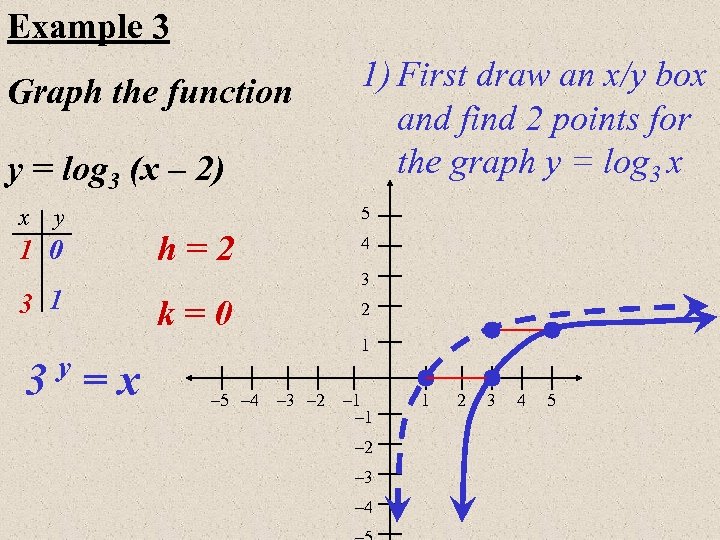Example 3 Graph the function y = log 3 (x – 2) x y 1 0 3 1 5 h=2 4 3 k=0 2 1 y 3 =x 1) First draw an x/y box and find 2 points for the graph y = log 3 x – 5 – 4 – 3 – 2 – 1 – 2 – 3 – 4 1 2 3 4 5

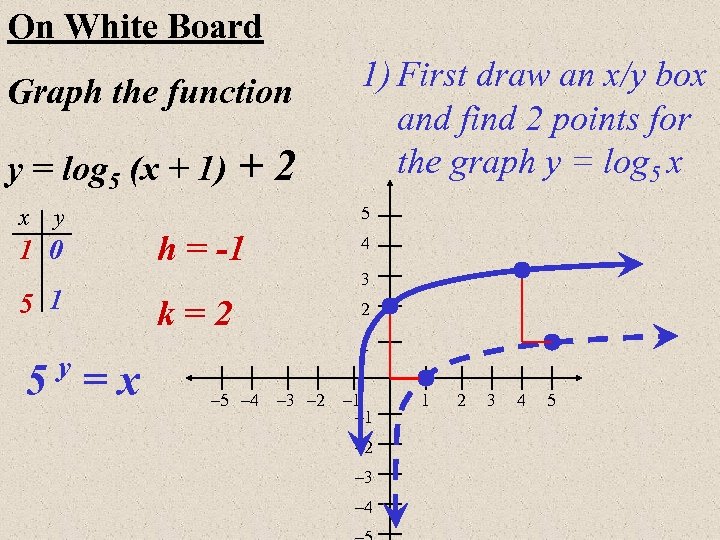On White Board Graph the function y = log 5 (x + 1) x y 1 0 5 1 +2 5 h = -1 4 3 k=2 2 1 y 5 =x 1) First draw an x/y box and find 2 points for the graph y = log 5 x – 5 – 4 – 3 – 2 – 1 – 2 – 3 – 4 1 2 3 4 5

With what we learned from 8. 3, simplify 1) log 100 + log 10, 000 (10 x = 100) and (10 x = 10, 000) x=2 and x=4 2+4=6 3) log 5 125 – log 5 25 3– 2=1 2) log 5 25 + log 5 125 (5 x = 25) and (5 x =125) x = 2 and x = 3 2+3=5 4) 2 • log 5 25 2 • 2=4

Objective – To be able to use properties of logarithms State Standard – 11. 0 Students will understand use simple laws of logarithms. Properties of Logarithms Product Property logb uv = logb u + logb v Quotient Property logb (u/v) = logb u - logb v Power Property logb un = n logb u

Example 1 State the property used: a. log 2 + log 3 = log 6 Product Property b. log 3 (x/y) = log 3 x – log 3 y Quotient Property c. log 4 (x 2 y) = 2 log 4 x + log 4 y Product and Power Property

Example 2 Expand log 5 2 x 6 Which property is being used? log 5 2 + log 5 x 6 log 5 2 + 6 log 5 x Product Property logb uv Power Property logb u n = logb u + logb v = n logb u

Example 3 Condense: 2 log 3 7 – 5 log 3 x = log 3 7 2 – log 3 x 2 = log 3 7 x 5 = log 3 49 x 5 5

On White Board Expand: log 5 3 r 4 = log 5 3 + log 5 r 4 = log 5 3 + 4 log 5 r

On White Board Condense: log 4 12 – log 4 2 = log 4 12 2 = log 4 6

1. Simplify 125 -2/3 1/ 2. Evaluate log 981 2 3. Evaluate log 28 3 25

8. 5 Solving Exponential and Logarithmic Equations Objective – Students will be able to solve exponential equations. CA State Standard – 11. 0 logarithms. Students use simple laws of

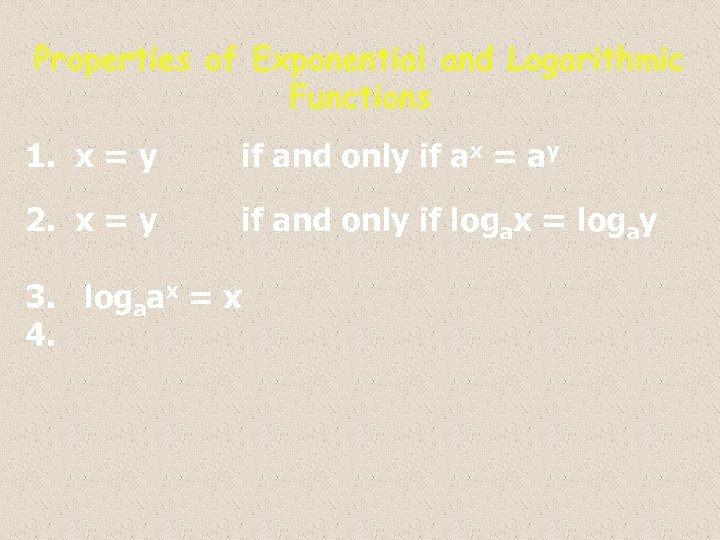Properties of Exponential and Logarithmic Functions 1. x = y if and only if ax = ay 2. x = y if and only if logax = logay 3. logaax = x 4.

Example 1 Evaluate 24 x = 32 x-1 4 x = 25(x-1) 2 4 x = 5 x – 5 +5 +5 4 x + 5 = 5 x -4 x 5=x

Change - of - Base Formula logc u =

Example 2 Evaluate 4 x = 15 x = log 15 log 44 4 x = log 415 log 15 x= log 4 x = 1. 95

Example 3 Evaluate log 4(x+3) = log 4(8 x+17) x + 3 = 8 x + 17 -x -x 3 = 7 x + 17 -17 -14 = 7 x x = -2