Explicit Exclusive Set Systems with Applications David P

Explicit Exclusive Set Systems with Applications David P. Woodruff Joint work with Craig Gentry and Zulfikar Ramzan

Outline 1. The Combinatorics Problem 2. Our Techniques 3. Applications 1. 2. 3. Broadcast encryption Certificate revocation Group testing

The Combinatorics Problem Ø Find a family C of subsets of {1, 2, …. , n} such that any large set S µ {1, 2, …, n} is the union of a small number of sets in C S = S 1 [ S 2 [ [ St Ø Parameters: Ø Universe is [n] = {1, …, n} Ø |S| >= n-r Ø Write S as a union of · t sets in C Ø Goal: Ø Minimize |C|

The Combinatorics Problem Ø Find a family C of subsets of [n] such that any set S µ [n] with |S| ¸ n-r is union of t sets in C: S = S 1 [ S 2 [ [ St Ø Example: t = 1 of size · r n Ø C excludes sets Ø C = all sets of size 1 n-r ¸ Ø C is an exclusive set system Ø|C| = n

Another Example Ø Example: r = 1, t = 2 Ø Write each i 2 [n] as (i 1, i 2) 2 [n 1/2]2 … x S: 1 i excludes 1 st coordinate i 1 Ø |C| = 2 n 1/2 n = excludes 2 nd coordinate i 2

Another Example (Generalized) Ø r = 1, t · log n Ø Write each i 2 [n] as (i 1, i 2 , …, it) 2 [n 1/t]t Ø Sets in C are named (x, y) 2 [t] x [n 1/t] i 2 (x, y) iff ix y Ø |C| = tn 1/t Ø If S = [n] n i, S = (1, i 1) [ (2, i 2) [ … [ (t, it)

Example Summary Ø r arbitrary Ø Ø Ø t = 1: |C| = t = n: |C| = n t · log n Ø r = 1: |C| = tn 1/t How does |C| grow given n, r, and t?

A Lower Bound Claim: Proof: 1. At least sets of size ¸ n-r 2. Only 3. Thus, 4. Solve for |C| different unions

Example Summary Ø r arbitrary Ø Ø Ø t = 1: |C| = t = n: |C| = n tight t · log n Ø r = 1: |C| = tn 1/t tight What happens for arbitrary n, r, and t?

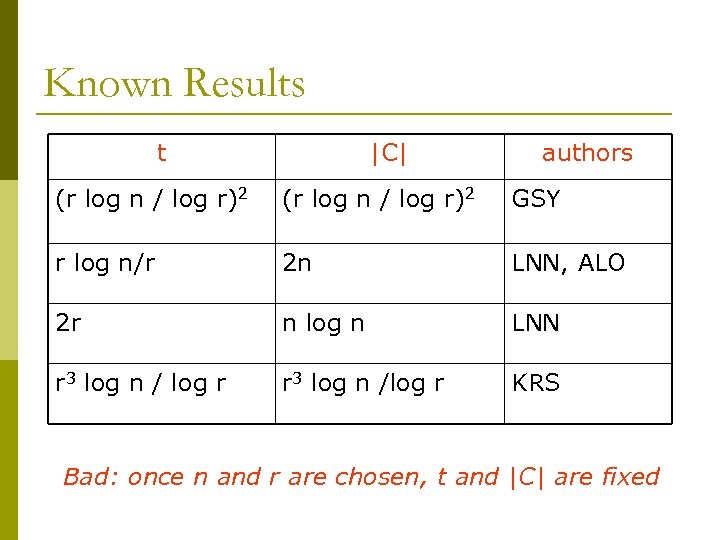Known Results t |C| authors (r log n / log r)2 GSY r log n/r 2 n LNN, ALO 2 r n log n LNN r 3 log n / log r r 3 log n /log r KRS Bad: once n and r are chosen, t and |C| are fixed

Known Results Ø Only known general result: Ø Ø If r · t, then |C| = O(t 3(nt)r/t log n) [KR] Drawbacks: Ø Ø Ø Probabilistic method To write S = S 1 [ S 2 [ … [ St , solve Set-Cover C has large description Bad for applications Suboptimal size:

Our Results Ø Main result: |C| = poly(r, t) Ø Ø Match lower bound up to poly(r, t) Ø Ø Ø n, r, t all arbitrary In applications r, t << n When r, t << n, get |C| = O(rt ) Our construction is explicit Ø Find sets S = S 1 [ … [ St in poly(r, t, log n) time Ø Improved cryptographic applications

Outline 1. The Combinatorics Problem 2. Our Techniques 3. Applications 1. 2. 3. Broadcast encryption Certificate revocation Group testing

Techniques Ø Case analysis: Ø r, t << n: algebraic solution Ø general r, t: use divide-and-conquer approach to reduce to previous case

Case: r, t << n Ø Find a prime p = n 1/t + Ø Integers [n] are points in (Fp)t Ø Consider the ring Fp[X 1, …, Xt] Ø Goal: find set of polynomials C such that for any R ½ [n] with |R| · r, there exist p 1, …, pt 2 C such that R = Variety(p 1, …, pt)

The Polynomial Collection Ø Consider the following collection: and

The Polynomial Collection (Con’d) and Proof: choose j=1|R| (X 1 – uj 1) Claim: If no two points in R have the same ith coordinate for any ith coordinates let ui 1, ui 2, …, ui|R| be thei, then we can find p 1, …, pt with Variety(p 1, …, pt) = R and ui+11, ui+12, …, ui+1|R| be the (i+1)st coordinates choose pi+1 = f(Xi) – Xi+1 by interpolating from f(uij) = ui+1 j for all j

The Polynomial Collection (Con’d) Proof: choose j=1|R| (X 1 – uj 1) let ui 1, ui 2, …, ui|R| be the ith coordinates and ui+11, ui+12, …, ui+1|R| be the (i+1)st coordinates choose pi+1 = f(Xi) – Xi+1 by interpolating from f(uij) = uij+1 for all j Claim 2: Induction. n. If x then x not in Variety(p 1, …, pjt) If x 2 [n] R, in Proof: 1: Every point in Rvariety, x 1 = u 1 j, for some Proof: Immediate Claim is in Variety(p 1 …, pt) pi+1(x) = f(xi) – xi+1 = 0 so: f(xi) = f(uij) = ui+1 j = xi+1

The Polynomial Collection (Con’d) and Ø |C| = O(tpr), where p = n 1/t + Ø Density theorems ! |C| = O(tnr/t) Ø Only works if R has distinct coordinates…

Handling Non-distinct Coordinates Ø Perform coordinate tranformations Ø Each u 2 [n] is a degree-(t-1) polynomial pu in Fp[x] Ø Translate polynomial representation to point representation by evaluation: pu -> (pu(1), pu(2), …, pu(t)) pu pu’ implies translations are distinct Ø Idea: choose many transformations (sets of t points in F p), so every R has a transformation with distinct coordinates Ø Apply previous construction

Handling Non-distinct Coordinates Suppose R = {1, …, r} 1 2 3 … t (t+1) (t+2) … 2 t (2 t+1) … … p 1 1 2 3 … t (t+1) (t+2) … 2 t (2 t+1) … … p 2 2 2 3 … t p 3 3 2 3 … t … pr r 2 3 … t …… ……

Handling Non-Distinct Coordinates Ø How many blocks of t points do we need to consider? Ø Two distinct degree-(t-1) polynomials can agree on at most t-1 points. Ø Thus, at most coordinates Ø So choose blocks, apply “distinct coordinate” construction for each block Ø Take union of constructions for all blocks can have non-distinct

Summary and Improvements Ø O(r 2 t) blocks, each O(t nr/t) sets Ø O(r 2 t 2 nr/t) sets in total! Ø Can improve to O(rt )

Improvements Ø Choose special points in Fp for blocks Ø Mix the blocks with an expander Ø Balance complexity of two types of sets

General n, r, t 1 x xxx i j x x n Ø Problem! n 2 term ? !? Ø Let m be such that r/m, t/m << n Ø Fix: - hash [n] to [r 2] first Ø For every interval [i, j], form an exclusive set system enough = j-i+1, so = r/m, t’an injective - do with n’ hashes r’ there is = t/m hash for every R Ø Given a set R, find intervals which evenly partition R. - apply construction above on [r 2]

Outline 1. The Combinatorics Problem 2. Our Techniques 3. Applications 1. 2. 3. Broadcast encryption Certificate revocation Group testing

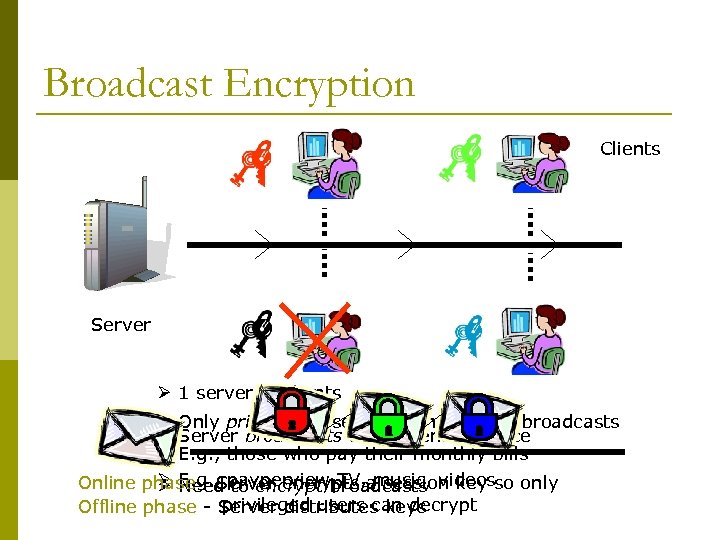Broadcast Encryption Clients Server Ø 1 server, n clients Ø Only privileged users can understand broadcasts Ø Server broadcasts to all clients at once Ø E. g. , those who pay their monthly bills Ø E. g. , payperviewbroadcasts videos Online phase - Server encrypts a session key so only Ø Need to encrypt TV, music, privileged users can decrypt Offline phase - Server distributes keys

Subset Cover Framework [NNL] Ø Offline stage: Ø For some S ½ [n], server creates a key K(S) and distributes it to all users in S Ø Idea: choose sets S from an exclusive set system C Ø Server space complexity ~ |C| Ø ith user space complexity ~ # S containing i

Subset Cover Framework [NNL] Ø Online stage: Ø Given a set R ½ [n] of at most r revoked users Ø Server establishes a session key M that only users in the set [n] n R know Ø Finds S 1, …, St with [n] n R = S 1 [ … [ St Encrypt M under each of K(S 1), …, K(St) Ø For u 2 [n] n R, there is Si with u 2 Si Ø For u 2 R, no Si with u 2 Si Ø Ø Content encrypted using session key M

Subset Cover Framework [NNL] Ø Online stage: Ø Communication complexity ~ t Ø Tolerate up to r revoked users Ø Tolerate any number of colluders Ø Information-theoretic security

Our Results Ø Use our explicit exclusive set system Ø General n, r, t Ø Contrasts with previous explicit systems Ø Poly(r, t, log n) time to find keys for broadcast Ø Contrasts with probabilistic constructions Ø Parameters Ø For poly(r, log n) server storage complexity, we can set t = r log (n/r), but previously t = (r 2 log n)

More Reasons to Study Exclusive Sets Ø Other applications Ø Ø Ø Certificate revocation Group testing Fun mathematical problem

Open problems Ø O(rt Ø Our O(rt ) versus (t ) ) bound needs t = o(log n) Ø Ø Ø Bound for general r, t is poly(r, t) Improve the poly(r, t) factor Find more applications